下载文档原格式
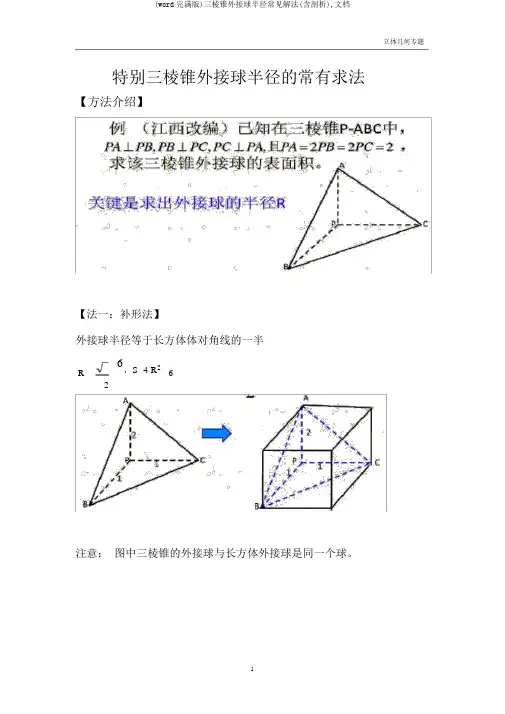
特别三棱锥外接球半径的常有求法【方法介绍】
【法一：补形法】
外接球半径等于长方体体对角线的一半
R
6
，S 4 R26 2
注意：图中三棱锥的外接球与长方体外接球是同一个球。
【法二：轴截面法】
1、搜寻底面△ PBC的外心；
2、过底面的外心作底面的垂线；
3、外接球的球心必在该垂线上，利用轴截面计算出球心的地址。
【法三：向量法】
设外接球的球心坐标为：O ( x, y, z) .由 OP OA OB OC 可得：
【方法总结】
三棱锥外接球半径的常见解法：
1、补形法；
2、轴截面法；
3、向量法 .
【练习坚固】
【参照答案】
练习 1【补形法】【轴截面法】
练习 2【补形法】【轴截面法】
练习 3【补形法】
练习 4【轴截面法】。
三棱锥外接球半径求法归纳对于简单多面体外接球的考查是近几年高考热点，其中又以对三棱锥外接球的考查居多，在学习了特殊三棱锥外接球半径的求法之后，我们应该进一步学习并归纳普通三棱锥外接球半径如何求解的问题，达到做一题知一类的目的。
对于特殊的三棱锥，我们可以通过补形的方法求其外接球的半径，比如正四面体我们曾经归纳过正四面体如图（1）外接球半径的求法,设正四面体的棱长为a，则可把该四面体补形成正方体（如图2），显然外接球直径为正方体对角线长，且正方体面对角线长为a，易得R＝a。
解跟球有关的问题,关键是寻找球心的位置,那么球心的位置有什么特殊性?关键点是满足到各顶点距离相等！可以先寻找底面三角形的外心，过底面外心作底面垂线，因为垂线上任意一点到底面各顶点距离相等，所以外接球球心必在该垂线上.如图3，在截面AED中，设AO=OD，即O为球心，在直角三角形OED中，D E＝a，AE＝a，OE=AE-R,，所以R2－（a-R）2＝|D E|2＝，解得R＝a，这种方法称为轴截面法(经过垂线和底面一个顶点的平面)，这种方法适合一般三棱锥.我们还学过两个结论.三条侧棱互相垂直的三棱锥的外接球：①如果三棱锥的三条侧棱互相垂直并且相等，则可以补形为一个正方体，正方体的外接球的球心就是三棱锥的外接球的球心．即三棱锥A1AB1D1的外接球的球心和正方体ABCDA1B1C1D1的外接球的球心重合．如图，设AA1＝a，则R＝a.②如果三棱锥的三条侧棱互相垂直但不相等，则可以补形为一个长方体，长方体的外接球的球心就是三棱锥的外接球的球心．R2＝＝(l为长方体的体对角线长)．(简称补形法)也可以用轴截面法找到球心如图（4），设PA=AB=AC=a,则直角三角形ABC外心是BC中点D，过D作平面ABC的垂线DQ取DQ=PA，则球心为QO中点O，因为AD= ,则在直角三角形ADO中，，所以，若三条边PA、AB、AC不相等，也一样可以得到结论.以下是两题高考题原题，我们利用归纳的方法很快能够解决：1．（2017全国卷1变式）在三棱锥 A- BCD 中， AC =CD = ，AB = AD = BD = BC = 1，若三棱锥的所有顶点都在同一个球面上，则球的表面积是_________．解：由已知可得BC ⊥AB, BC ⊥BD ，所以BC ⊥平面 ABD ，且底面ABC是正三角形，只需过底面三角形外心作底面垂线，且，则球心为的中点O，在直角三角形中，，，所以所以球的表面积为2．已知是球面上不共面的四点，，平面平面，则此球的体积为_________．解:由题意可知三角形ABC是等腰直角三角形，三角形BDC是等腰三角形，所以球心在过BC中点E且垂直平面ABC的垂线上，因为平面平面，所以DE垂直平面ABC，由于DE，OC=R，解得所以这两题关键点是根据题意先找出几何体的线面,面面的垂直关系,然后作出比较直观的图形,不难发现仍然可以用轴截面找球心的方法完成.我们对问题的解决和方法的生成都是一步一步完成的,对本节的主要方法补形法和轴截面法能很好的总结并加以应用.。
正棱锥外接球半径公式推导
嘿，咱今儿就来好好唠唠正棱锥外接球半径公式推导这事儿！正棱锥外接球半径公式呢，就像是一把钥匙，能帮我们打开理解正棱锥和外接球关系的大门。
先来说说正三棱锥的情况，设正三棱锥底面边长为 a，高为 h，那外接球半径 R 可以通过这样一个公式来算：R = √[(h^2 + (a√3/3)^2) / 2]。
比如说一个正三棱锥，底面边长是 6，高是 8，那我们就能算出它的外接球半
径啦！
再看看正四棱锥，它的外接球半径公式又有些不同呢！哎，你说数学这东西是不是很神奇呀，就像一个神秘的宝藏等着我们去挖掘！好比我们有一个正四棱锥，底面边长为 b，高为 H，那外接球半径 R 就等于√[(H^2 + (b/2)^2)]。
就像我们找到了打开宝藏的密码一样让人兴奋呀！
其实这外接球半径的推导啊，就好比我们盖房子，得先打好基础，一步一步来，才能找到那个最合适的结果。
不是吗？咱可得把这些公式好好记住，然后用它们去解决各种有趣的问题，你说好不好呀！。
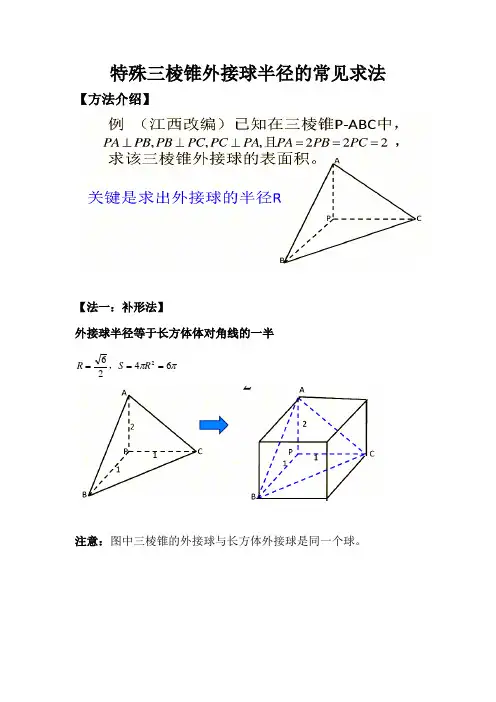
特殊三棱锥外接球半径的常见求法
【方法介绍】
【法一：补形法】
外接球半径等于长方体体对角线的一半
ππ642
6
2===
R S R ，
注意：图中三棱锥的外接球与长方体外接球是同一个球。
【法二：轴截面法】
1、 寻找底面△PBC 的外心；
2、 过底面的外心作底面的垂线；
3、 外接球的球心必在该垂线上，利用轴截面计算出球心的位置。
【法三：向量法】
设外接球的球心坐标为：),,(z y x O .由→
→
→
→
===OC OB OA OP 可得：
【方法总结】
三棱锥外接球半径的常见解法：
1、 补形法；
2、轴截面法；
3、向量法.
【练习巩固】
【参考答案】
练习1 【补形法】【轴截面法】
【轴截面法】
练习3 【补形法】。
三棱锥外接球公式三棱锥外接球公式，是描述三棱锥与外接球之间的关系的数学公式。
在几何学中，三棱锥是一种四面体，它有三个侧面和一个底面，底面是一个三角形。
外接球是一个与三棱锥的四个顶点都相切的球。
三棱锥外接球公式可以用来计算外接球的半径。
在了解三棱锥外接球公式之前，我们先来了解一下三棱锥和外接球的基本概念。
三棱锥是一个四面体，它有一个底面和三个侧面。
底面是一个三角形，侧面是连接底面顶点和一个共同顶点的三个三角形。
外接球是一个与三棱锥的四个顶点都相切的球，也就是说，外接球的球心正好在三棱锥的顶点上。
根据三棱锥外接球公式，我们可以计算外接球的半径。
这个公式的表达式为：R = a / (2 * √3)，其中R代表外接球的半径，a代表三棱锥的边长。
通过这个公式，我们可以根据三棱锥的边长来计算外接球的半径。
三棱锥外接球公式的推导过程比较复杂，这里不做详细介绍。
但是我们可以通过一些几何性质来理解这个公式的原理。
首先，我们知道三棱锥的底面是一个三角形，而外接球与三角形的三个顶点都相切。
根据几何性质，三角形的外接圆的圆心和三角形的三个顶点所在直线的交点是共线的。
所以，外接球的球心必须在三棱锥的顶点所在的直线上。
而且，由于外接球与三棱锥的四个顶点都相切，所以外接球的球心和顶点之间的距离必须相等。
根据几何性质，这个距离正好等于三棱锥的高。
而三棱锥的高可以通过边长和底面的面积计算得到。
通过这些几何性质，我们可以推导出三棱锥外接球公式。
首先，我们根据三棱锥的边长和底面的面积计算出三棱锥的高。
然后，根据三棱锥的高和顶点到球心的距离相等的性质，我们可以计算出外接球的半径。
三棱锥外接球公式的应用范围非常广泛。
在几何学和工程学中，我们经常需要计算三棱锥的各种属性，比如体积、表面积等。
而外接球的半径是三棱锥的一个重要属性，它可以帮助我们计算其他与三棱锥相关的量。
所以，掌握三棱锥外接球公式对于理解和应用几何学和工程学知识非常重要。
总结起来，三棱锥外接球公式是描述三棱锥与外接球之间关系的数学公式。
正三棱锥外接球半径公式1. 认识正三棱锥嘿，朋友们，今天我们要聊聊一个有趣的几何小家伙——正三棱锥。
说到这儿，可能有的人会皱皱眉，心里想着，“这又是什么鬼？”其实，正三棱锥就是一个底面是正三角形的金字塔，顶端像个尖尖的帽子，底下则是稳稳的三角形。
简单来说，它的底面有三个边，三个角，给人一种“对称、和谐”的美感。
想象一下，如果你在建筑设计上运用它，那可真是炫酷得不行啊！不过，今天我们可不只是来欣赏这位几何小明星的美丽外表，咱们还得深入挖掘它的内在——特别是它的外接球半径。
2. 外接球半径的概念2.1 什么是外接球？那么，外接球又是什么呢？简单来说，外接球就是一个球，可以把正三棱锥“包”住，就像把一个苹果放进袋子里。
它的表面会与正三棱锥的所有顶点相切。
想象一下，如果你把这个三棱锥放进一个球里，那个球的表面正好碰到三棱锥的三个顶点，嘿，这就是外接球！可好玩了。
2.2 为什么要计算半径？可能有小伙伴会问：“这外接球半径有什么用呢？”哦，亲爱的，别小看这个小小的半径，它可是几何界的“万金油”！无论是在建筑、工程，还是在很多设计中，外接球半径都能帮我们确定形状的大小和稳定性。
比如说，要设计一个完美的水池，或者雕塑一个独特的艺术品，知道这个半径可真是事半功倍！3. 外接球半径公式3.1 公式的推导好，咱们来聊聊这个神秘的外接球半径公式。
你可能会问，“这公式是怎么来的？”其实，这个公式可不是随便来的，背后有一套完整的推导过程。
我们先设这个正三棱锥的底面边长为 ( a )，高为 ( h )。
那么，外接球半径 ( R ) 的计算公式是：R = frac{sqrt{6{3 cdot frac{a{sqrt{3 + 1 + frac{h{3。
这个公式虽然看起来有点复杂，但其实也没什么大不了的。
我们把边长和高度放进去，就能得到球的半径了。
3.2 公式的应用当我们把数据代入公式后，结果会告诉我们，这个正三棱锥外接的球有多大。
话题：两两垂直的三棱锥外接球半径公式探讨一、引言在数学中，三棱锥是一种常见的几何体，它由一个三角形作为底面和三条边共点的一点构成。
而外接球则是指能够同时与某一几何体的所有顶点相切的球。
本文将探讨两两垂直的三棱锥外接球的半径公式，并尝试从简单到复杂的角度，对此进行全面评估和阐释。
二、两两垂直的三棱锥外接球半径公式初探在几何学中，关于两两垂直的三棱锥外接球半径的公式，可以通过直观的推导和简单的图解进行初步理解。
假设三棱锥的底面为等边三角形ABC，顶点为O，而外接球的半径为R。
对于两两垂直的三棱锥，我们可以得到以下初步公式：1. 半径R与三棱锥的高h相关，表达为 R = k * h，其中k为系数。
2. 通过多次试验和实验，我们可以得出k与三棱锥的形状、底面三角形的边长、以及顶点到底面的距离等因素相关。
这是初步探索的一部分内容。
三、深入探讨如果想要更深入地理解两两垂直的三棱锥外接球半径公式，我们需要对三棱锥的几何特性和球的性质进行更加深入的分析。
这包括但不限于：1. 三棱锥的高和底面三角形的关系：高和底面三角形的边长、角度以及其他相关因素是如何影响外接球半径的。
2. 多个三棱锥的组合：如果存在多个两两垂直的三棱锥，它们的外接球是否存在某种联系，其半径之间是否存在某种规律，这也是我们应该深入探讨的方向。
3. 对于球体的性质，例如球面积、球体积的公式，以及对球面的切割等也是进行深入探讨的一部分。
通过深入探讨，我们可以更好地理解两两垂直的三棱锥外接球半径的公式，也能够更好地掌握这一数学知识。
四、总结与回顾在本文中，我们对两两垂直的三棱锥外接球半径的公式进行了初步探讨，并逐步深入分析了相关的数学知识。
我们从简单的图解、初步推导开始，逐步深入，探讨了三棱锥的几何特性、外接球的性质以及与球体相关的数学问题。
通过本文的阐述，我们对于两两垂直的三棱锥外接球的相关知识有了更深入的了解。
五、个人观点与理解在我看来，数学是一门神奇而美妙的学科，它的奥秘和魅力无穷。
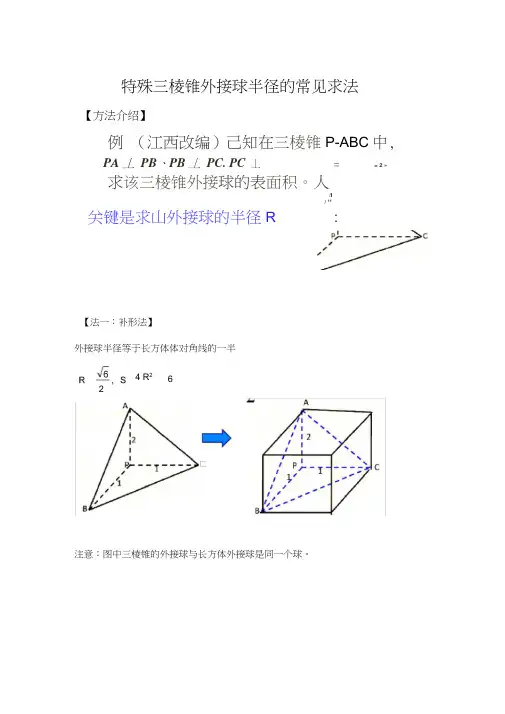
特殊三棱锥外接球半径的常见求法
【方法介绍】
例（江西改编）己知在三棱锥P-ABC中, PA 丄PB、PB 丄PC. PC丄= = 2 »
求该三棱锥外接球的表面积。
人
/I
/ 11
关键是求山外接球的半径R :
【法一：补形法】
外接球半径等于长方体体对角线的一半
4 R26
2
匚
注意：图中三棱锥的外接球与长方体外接球是同一个球。
【法二：轴截面法】
1、寻找底面厶PBC勺外心；
2、过底面的外心作底面的垂线;
3、外接球的球心必在该垂线上，利用轴截面计算出球心的位置
【法三：向量法】
【方法总结】
三棱锥外接球半径的常见解法:
1、补形法； 2 、轴截面法； 3 、向量法.
【练习巩固】
练习1 （陕西，2010）如图，在三棱锥P-ABC 中，刊丄平血丄丄加、且E4二2肋二2BC二2 ,
求其外接球的体积。
练习2 （全国卷，2010）已知三棱锥的各条棱长均为1,求其外接球的表面积。
练习3 （河北，二012）如图，在四面体ABCD 中MB二DC二俪，AD二BC二0D二AC二屈, 求其外接球的表面积。
练习4如图，已知三棱锥P-ABC中，PA丄底面ABC, PA=AB=AC=2, ZBAC二120 ,求其夕卜接球的半径。
【参考答案】
0A=0B=0C=0P
练习3 【补形法】
A
S = 47rR2 = 14TT。
