下载文档原格式
正三棱锥外接球半径求法今天咱们来唠唠正三棱锥外接球半径的求法。
这可是个很有趣的数学小知识呢！一、什么是正三棱锥。
正三棱锥呢，就是底面是正三角形，然后从底面的中心向顶点引一条垂线，这个顶点在底面上的射影就是底面正三角形的中心。
它的四个面可都是全等的等腰三角形哦。
这就像一个超级稳定的小金字塔一样，特别神奇。
二、外接球的概念。
那外接球是啥呢？就是这个正三棱锥在一个球里面，这个球刚刚好把正三棱锥给包起来，这个球就叫做正三棱锥的外接球。
就好像给这个正三棱锥穿上了一个圆圆的大外套，这个外套的半径就是我们要找的外接球半径啦。
三、求外接球半径的方法。
1. 补形法。
这是一个很巧妙的方法哦。
咱们可以把正三棱锥补成一个正方体或者是直三棱柱。
比如说补成正方体的时候，正三棱锥的外接球其实就是这个正方体的外接球。
为啥能这么补呢？这就像是把零散的小零件组合成一个大的整体，然后利用这个大整体的性质来求我们想要的东西。
如果正三棱锥的棱长是a，补成正方体后，正方体的棱长设为x，我们可以通过一些几何关系找到它们之间的联系，然后根据正方体的外接球半径公式R = 棱长×√3/2（这里的棱长就是正方体的棱长x），再把x用a表示出来，就能求出正三棱锥外接球的半径啦。
2. 直接法。
这个方法就比较直接啦。
我们要先找到正三棱锥底面三角形的中心O₁，然后连接顶点和这个中心得到一条线，设正三棱锥的高为h，底面正三角形的边长为a。
底面正三角形中心到底面顶点的距离可以根据正三角形的性质求出来，是√3a/3。
然后我们设外接球的球心为O，球心O可能在正三棱锥的内部或者外部。
根据勾股定理，在直角三角形OO₁A（A是底面三角形的一个顶点）中，OA就是外接球的半径R，我们可以得到一个等式：R²=(h - R)²+(√3a/3)²（当球心在正三棱锥内部的时候）或者R²=(R - h)²+(√3a/3)²（当球心在正三棱锥外部的时候），然后解这个方程就可以求出外接球的半径R啦。
三棱锥外接球半径常见解法三棱锥是立体几何中最具挑战性的几何形体之一，它具有奇妙的几何美，是许多数学家和几何学家的景点和玩游戏的佳境。
学习解决三棱锥外接球半径的问题，给人带来一种全新的愉悦感。
三棱锥外接球半径的概念有多个描述。
它定义为将一个三棱锥置于某种情况中的最小球体的半径。
三棱锥可以由三条 / 有关的侧延长线构成，或三角形的底部和顶部来构建。
因此，三棱锥外接球半径因其外表形状而变化。
最经典的解决三棱锥外接球半径问题的方法是利用几何进行计算。
该方法主要利用三角函数来检验三角形底部给定点和外接球中心之间的距离。
首先，三角形的底面上的三点应该被指定。
这三点成为被研究三角形的顶点。
以此为基础，计算三个顶点的位置，并确定它们的关系，以确定三边的范围。
当三边的范围被确定以后，通过三角原理，可以得出中线边的长度，并以此决定外接球的半径。
通过三角函数，还可以确定外接球与三角形底部点之间的坐标距离。
首先，应该找出两个顶点形成的直角边的斜率，并利用其斜率式定义斜线方程。
这样就可以展开对应的三角函数，并根据相应的函数求出外接球的中心点与底部点的坐标距离。
另一种解决三棱锥外接球半径问题的方法是借助几何软件。
几何软件提供三棱锥具体定义，并支持求解三棱锥外接球半径的功能，使用者可以更加方便快捷地获得所需要的数据。
通过利用几何软件解决三棱锥外接球半径问题，只需输入三角形底面上的三点坐标即可用几何软件计算出三棱锥外接球半径。
用户还可以根据所输入的点的值，计算出三角形底面的长和宽，从而得出外接球的半径。
当外接球的半径计算出来以后，用户将获得一个完整的三棱锥外接球的数据，借此可以通过算法模拟三棱锥的外观以及三棱锥与球体的关系，为研究三棱锥的几何性质提供参考。
以上就是三棱锥外接球半径常见解法的介绍，它是一种有趣却又挑战性强的数学问题，让人有种新奇解决前所未有问题的乐趣。
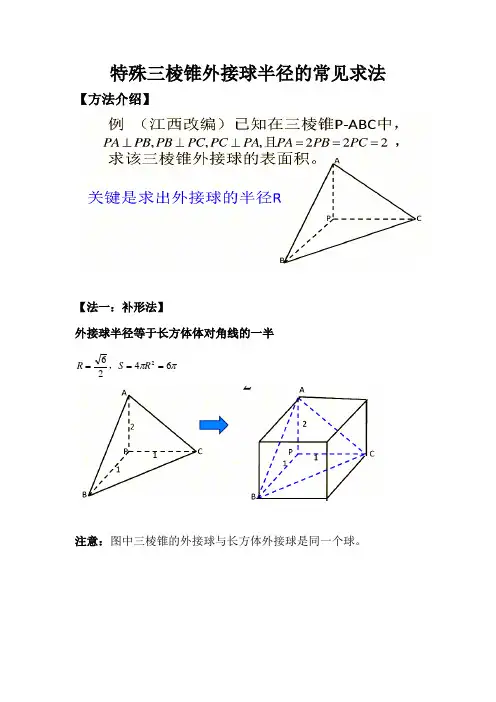
特殊三棱锥外接球半径的常见求法
【方法介绍】
【法一：补形法】
外接球半径等于长方体体对角线的一半
ππ642
6
2===
R S R ，
注意：图中三棱锥的外接球与长方体外接球是同一个球。
【法二：轴截面法】
1、 寻找底面△PBC 的外心；
2、 过底面的外心作底面的垂线；
3、 外接球的球心必在该垂线上，利用轴截面计算出球心的位置。
【法三：向量法】
设外接球的球心坐标为：),,(z y x O .由→
→
→
→
===OC OB OA OP 可得：
【方法总结】
三棱锥外接球半径的常见解法：
1、 补形法；
2、轴截面法；
3、向量法.
【练习巩固】
【参考答案】
练习1 【补形法】【轴截面法】
【轴截面法】
练习3 【补形法】。
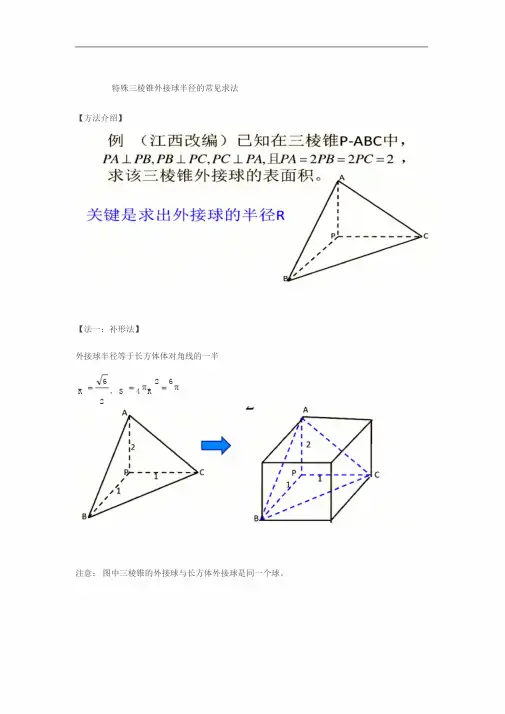
特殊三棱锥外接球半径的常见求法
【方法介绍】
【法一：补形法】
外接球半径等于长方体体对角线的一半
6
6 2
R ，S 4 R
2
注意：图中三棱锥的外接球与长方体外接球是同一个球。
【法二：轴截面法】
1、寻找底面△PBC 的外心；
2、过底面的外心作底面的垂线；
3、外接球的球心必在该垂线上，利用轴截面计算出球心的位置。
【法三：向量法】
设外接球的球心坐标为：O( x, y, z) .由OP OA OB OC 可得：
【方法总结】
三棱锥外接球半径的常见解法：
1、补形法；
2、轴截面法；
3、向量法. 【练习巩固】
【参考答案】
练习 1 【补形法】【轴截面法】
练习 2 【补形法】【轴截面法】
练习 3 【补形法】
练习 4 【轴截面法】
您好，欢迎您阅读我的文章，本 WORD 文档可编辑修改，也可以直接打印。
阅读过后，希望您提出保贵的意见或建议。
阅读和学习是一种非常好的习惯，坚持下去，让我们共同进步。
几何体外接球常用结论及方法(如何求几何体的外接球半径)几何体的外接球是一个常见的问题，其中有一些常用的结论和方法：1.对于三棱锥P-ABC，如果PA垂直于PB和PC，则该三棱锥的外接球半径2R可以用公式2R=PA²+PB²+PC²求得。
2.对于等边三角形，其外接圆的半径等于连长的1/3倍。
3.直角三角形的外接圆半径等于斜边的一半。
4.对于一般的三角形ABC，可以用正弦定理求得外接圆半径R，而内切圆的半径r可以用海龙公式S=Cr求得。
5.如果已知三棱锥P-ABC中PA=a，且△ABC的外接圆半径为r，则该三棱锥的外接球半径2R可以用公式2R=2r+a²求得。
6.正方体的外接球、内切球和棱切球的直径分别为正方体的体对角线长2R=3a、棱长2R=a和面对角线长2R=2√2a。
7.对于四面体P-ABC，如果∠APC=90°且∠ABC=90°，则该四面体的外接球直径为AC。
8.对于正三棱锥V-ABC，可以用射影定理求得其外接球半径，即VA²=h(2R-h)。
9.对于正四面体，其高h=2/3√2a，外接球半径和内切球半径均为a。
10.对于有内切球的多面体，其内切球半径可以用公式V=Sr/3求得。
11.如果三棱锥A-BCD中的面ABD和面BCD互相垂直且其外接圆半径分别为r1和r2，公共棱BD的长度为a，则该三棱锥的外接球半径2R可以用公式2R=2r1+2r2-a²/2√(r1²+r2²)求得。
的公共弦AD和BC的垂线，分别交于点E和F。
连接OE和OF，则OE=OF=R，且OE和OF分别是三棱锥P-ABC 和A-BCD的外接球的直径。
由于三棱锥P-ABC和A-BCD的外接球是重合的，因此它们的直径相等，即2R=2r1+2r2-a。
对于三棱锥P-ABC，已知面PAC与ABC所形成的二面角为θ（θ<θ≤90°），且已知ΔPAC和ΔABC的外接圆的半径分别为r1，r2，AC=a，则该棱锥的外接球半径R满足：left(2R+2\cos\theta\right)\left(R-r_1\right)\left(R-r_2\right)=2\left(r_1+r_2\right)^2-4\left(r_1-r_2\right)^2\cos^2\frac{\theta}{2}$这个公式可以通过对三棱锥P-ABC和A-BCD的共面直角投影，推导出它们的公共弦长等于$\sqrt{a^2+\left(r_1+r_2\right)^2-2r_1r_2\cos\theta}$。
特殊三棱锥外接球半径的常见求法
【法一：补形法】
外接球半径等于长方体体对角线的一半
ππ642
62===R S R ，
注意：图中三棱锥的外接球与长方体外接球是同一个球。
【法二：轴截面法】
1、 寻找底面△PBC 的外心；
2、 过底面的外心作底面的垂线；
外接球的球心必在该垂线上，利用轴截面计算出球心的 图画捉迷藏 美少女2 幼儿读物少儿益智游戏 逻辑思维训练书籍
3、 位置。
【法三：向量法】
设外接球的球心坐标为：),,(z y x O .由→
→→→===OC OB OA OP 可得：
【练习巩固】
【参考答案】
练习1 【补形法】【轴截面法】
练习2 【补形法】【轴截面法】
练习3 【补形法】。
特殊三棱锥外接球半径的常见求法【法一：补形法】
外接球半径等于长方体体对角线的一半
注意：图中三棱锥的外接球与长方体外接球是同一个球。
【法二：轴截面法】
1、寻找底面厶PBC的外心；
2、过底面的外心作底面的垂线；
外接球的球心必在该垂线上，利用轴截面计算出球心的
图画捉迷藏美少女2幼儿读物少儿益智游戏逻辑思维训练书籍
3、位置。
【法三：向量法】
【练习巩固】
练习1 （陕西，2010）如图，在三棱锥P-ABC 中，朋丄平^ABC^CBLPB.CB丄加•且E4二2加二2BC二2 , 求其外接球的体积。
P
练习2 （全国卷，2010）已知三棱锥的各条 棱长均为求其外接球的表面积。
练习3 （河北，2012）如图，在四面体ABCD 中,AB 二DC 二逐,AD 二BC 二&BD 二AC 二屈,
求其外接球的表面积。
【参考答案】
练习1【补形法】
【轴截面法】
0A 二OB 二
0C 二OP
晶兀
练习2 【补形法】
R = -------- 、 S = A-TT R 2
= 14?r 2
D A A 【轴截面法】
D A。
三棱锥外接球半径常见解法含答案解析在立体几何中，求三棱锥外接球半径是一个常见且重要的问题。
掌握有效的解法不仅能够帮助我们解决具体的数学题目，还能加深对空间几何关系的理解。
下面将为大家介绍几种常见的求解三棱锥外接球半径的方法，并通过具体的例子进行答案解析。
一、补形法补形法是一种常用的技巧，通过将三棱锥补成一个特殊的几何体，如长方体、正方体等，然后利用这些特殊几何体的外接球半径与原三棱锥外接球半径的关系来求解。
例如，对于墙角三棱锥（三条侧棱两两垂直的三棱锥），我们可以将其补成长方体。
设三棱锥的三条侧棱长分别为＼（a\）、＼（b\）、＼（c\），则长方体的体对角线就是三棱锥外接球的直径＼（2R\），根据长方体体对角线公式可得：＼＼begin{align}2R&＝＼sqrt{a^2 ＋ b^2 ＋ c^2}＼＼R&＝＼frac{＼sqrt{a^2 ＋ b^2 ＋ c^2}｝｛2}＼end{align}＼例 1：已知三棱锥＼（P ABC\）中，＼（PA\perp PB\），＼（PB\perp PC\），＼（PC\perp PA\），且＼（PA ＝ 3\），＼（PB ＝4\），＼（PC ＝ 5\），求其外接球半径。
解：将三棱锥＼（P ABC\）补成长方体，长方体的体对角线就是外接球的直径。
＼＼begin{align}2R&＝＼sqrt{3^2 ＋ 4^2 ＋ 5^2}＼＼＆＝＼sqrt{9 ＋ 16 ＋ 25}＼＼＆＝＼sqrt{50}＼＼＆＝5\sqrt{2}＼end{align}＼所以，外接球半径＼（R ＝＼frac{5\sqrt{2}｝｛2}＼）二、确定球心位置法通过寻找三棱锥外接球的球心位置，利用球心到各顶点的距离等于外接球半径来求解。
对于正三棱锥，球心通常在高线上。
设正三棱锥底面边长为＼（a\），高为＼（h\），底面外接圆半径为＼（r\）（可由正弦定理求得＼（r ＝＼frac{＼sqrt{3}｝｛3}a\）），球心到底面距离为＼（d\），则根据勾股定理有：＼＼begin{align}R^2&＝d^2 ＋ r^2\＼d&＝h R＼end{align}＼联立可得＼（R\）的表达式。
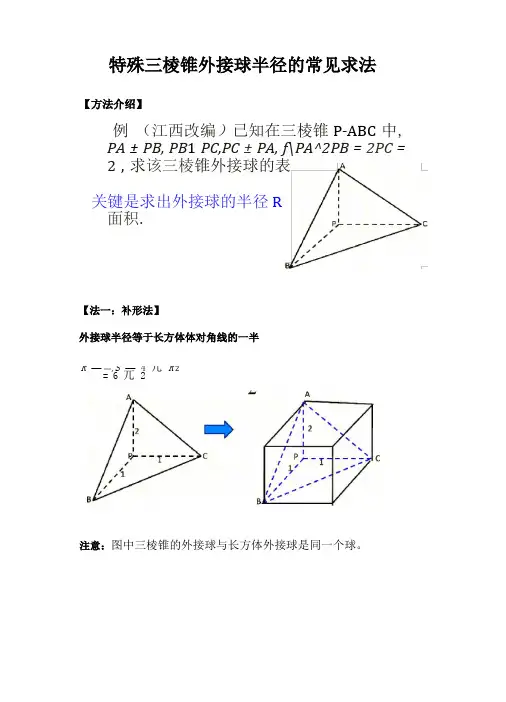
特殊三棱锥外接球半径的常见求法
【方法介绍】
例（江西改编）已知在三棱锥P-ABC中, PA ±PB, PB1 PC,PC ±PA, f\PA^2PB = 2PC =
2 , 求该三棱锥外接球的表
关键是求出外接球的半径R
面积.
【法一：补形法】
外接球半径等于长方体体对角线的一半
R ——, S — 4 兀R 2
= 6 兀2
注意：图中三棱锥的外接球与长方体外接球是同一个球。
【法二：轴截面法】
1、寻找底面^PBC的外心；
2、过底面的外心作底面的垂线;
3、外接球的球心必在该垂线上，利用轴截面计算出球心的位置。
【法三：向量法】
设外接球的球心坐标为：O(x, y, z).由力二由二OB二”可
得:
【方法总结】
三棱锥外接球半径的常见解法:
1、补形法；
2、轴截面法；
3、向量
法.
【练习巩固】
练习2 （全国卷，2010）已知三棱锥
的各条棱长均为工，求其外接球的表
面积。
练习3 （河北，2012）如图,在四面体ABCD 中，M二DC二回，助二BC二6即二AC二屈，求其外接球的表面积口.
练习4如图, 面ABC, PA=A 【接球的半径。
【参考答案】练习1【补形法】
R当v=【轴截面法】
( R 二;CP
已知三棱锥P-ABC中，PA_L 底
3HAe=2, NBAC=1201求其外
C 1 B
-TrR) =«7T
- 8
0A =OB=OC=OP
【轴截面法】
练习3【补形法】
B。
