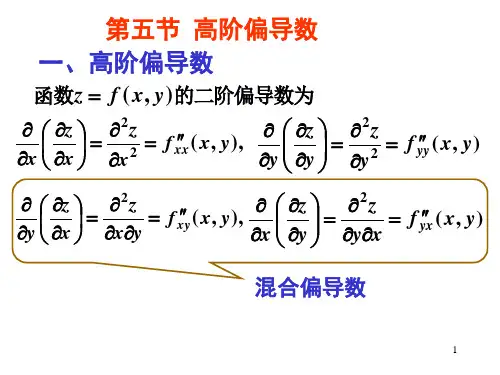
第五节高阶偏导数
- 格式:ppt
- 大小:390.57 KB
- 文档页数:13

第二节 偏导数教学目的:使学生了解偏导数的概念;熟练掌握一阶及二阶偏导数的计算方法;了解偏导数存在与函数连续的关系。
教学重点:一阶及二阶偏导数的计算 教学过程:一、偏导数的定义及其计算法对于二元函数z =f (x , y ), 如果只有自变量x 变化, 而自变量y 固定, 这时它就是x 的一元函数, 这函数对x 的导数, 就称为二元函数z =f (x , y )对于x 的偏导数. 定义 设函数z =f (x , y )在点(x 0, y 0)的某一邻域内有定义, 当y 固定在y 0而x 在x 0处有增量∆x 时, 相应地函数有增量f (x 0+∆x , y 0)-f (x 0, y 0).如果极限x y x f y x x f x ∆-∆+→∆),(),(lim00000存在, 则称此极限为函数z =f (x , y )在点(x 0, y 0)处对x 的偏导数, 记作00y y x x x z==∂∂, 00y y x x x f ==∂∂, 00y y x x x z ==, 或),(00y x f x .例如x y x f y x x f y x f x x ∆-∆+=→∆),(),(lim),(0000000.类似地, 函数z =f (x , y )在点(x 0, y 0)处对y 的偏导数定义为y y x f y y x f y ∆-∆+→∆),(),(lim 00000,记作00y y x x y z==∂∂, 00y y x x y f ==∂∂, 00y y x x yz ==,或f y (x 0, y 0).偏导函数: 如果函数z =f (x , y )在区域D 内每一点(x , y )处对x 的偏导数都存在, 那么这个偏导数就是x 、y 的函数, 它就称为函数z =f (x , y )对自变量x 的偏导函数, 记作x z ∂∂, xf ∂∂, x z , 或),(y x f x.偏导函数的定义式: x y x f y x x f y x f x x ∆-∆+=→∆),(),(lim ),(0.类似地, 可定义函数z =f (x , y )对y 的偏导函数, 记为y z ∂∂, yf∂∂, z y , 或),(y x f y .偏导函数的定义式: y y x f y y x f y x f y y ∆-∆+=→∆),(),(lim ),(0.求xf∂∂时, 只要把y 暂时看作常量而对x 求导数; 求y f ∂∂时, 只要把x 暂时看作常量而对y 求导数.讨论: 下列求偏导数的方法是否正确?0),(),(00y y x x x x y x f y x f ===, 00),(),(00y y x x y y y x f y x f ===.0]),([),(000x x x y x f dxd y x f ==, 0]),([),(000y y y y x f dy d y x f ==.偏导数的概念还可推广到二元以上的函数. 例如三元函数u =f (x , y , z )在点(x , y , z )处对x 的偏导数定义为x z y x f z y x x f z y x f x x ∆-∆+=→∆),,(),,(lim ),,(0,其中(x , y , z )是函数u =f (x , y , z )的定义域的内点. 它们的求法也仍旧是一元函数的微分法问题.例1 求z =x 2+3xy +y 2在点(1, 2)处的偏导数. 解 y x x z 32+=∂∂, y x y z 23+=∂∂. 8231221=⋅+⋅=∂∂==y x x z,7221321=⋅+⋅=∂∂==y x yz .例2 求z =x 2sin 2y 的偏导数. 解 y x xz 2sin 2=∂∂, y x y z 2cos 22=∂∂.例3 设)1,0(≠>=x x x z y , 求证: z y z x x z y x 2ln 1=∂∂+∂∂.证 1-=∂∂y yx xz , x x y z y ln =∂∂.z x x x x x yx y x y z x x z y x y y y y 2ln ln 1ln 11=+=+=∂∂+∂∂-.例4 求222z y x r ++=的偏导数.解 r x z y x x x r =++=∂∂222; r y z y x y y r =++=∂∂222.例5 已知理想气体的状态方程为pV =RT (R 为常数),求证:1-=∂∂⋅∂∂⋅∂∂pTT V V p . 证 因为V RT p =, 2V RT V p-=∂∂; p RT V =, p R T V =∂∂;RpV T =, R V p T =∂∂; 所以12-=-=⋅⋅-=∂∂⋅∂∂⋅∂∂pV RT RV p R V RT p T T V V p . 例5 说明的问题: 偏导数的记号是一个整体记号, 不能看作分子分母之商. 二元函数z =f (x , y )在点(x 0, y 0)的偏导数的几何意义:f x (x 0, y 0)=[f (x , y 0)]x '是截线z =f (x , y 0)在点M 0处切线T x 对x 轴的斜率. f y (x 0, y 0) =[f (x 0, y )]y '是截线z =f (x 0, y )在点M 0处切线T y 对y 轴的斜率.偏导数与连续性: 对于多元函数来说, 即使各偏导数在某点都存在, 也不能保证函数在该点连续. 例如⎪⎩⎪⎨⎧=+≠++=000),(222222y x y x y x xy y x f在点(0, 0)有, f x (0, 0)=0, f y (0, 0)=0, 但函数在点(0, 0)并不连续. 提示:0)0 ,(=x f , 0) ,0(=y f ;0)]0 ,([)0 ,0(==x f dx d f x , 0)] ,0([)0 ,0(==y f dy d f y . 当点P (x , y )沿x 轴趋于点(0, 0)时, 有00lim )0 ,(lim ),(lim 0)0,0(),(===→→→x x y x x f y x f ;当点P (x , y )沿直线y =kx 趋于点(0, 0)时, 有22222022 )0,0(),(1lim lim kk x k x kx y x xy x kxy y x +=+=+→=→. 因此, ),(lim )0,0(),(y x f y x →不存在, 故函数f (x , y )在(0, 0)处不连续.类似地, 可定义函数z =f (x , y )对y 的偏导函数, 记为y z ∂∂, yf∂∂, z y , 或),(y x f y .偏导函数的定义式: yy x f y y x f y x f y y ∆-∆+=→∆),(),(lim),(0.二. 高阶偏导数 设函数z =f (x , y )在区域D 内具有偏导数),(y x f x z x=∂∂, ),(y x f y z y =∂∂,那么在D 内f x (x , y )、f y (x , y )都是x , y 的函数. 如果这两个函数的偏导数也存在, 则称它们是函数z =f (x , y )的二偏导数. 按照对变量求导次序的为同有下列四个二阶偏导数 如果函数z =f (x , y )在区域D 内的偏导数f x (x , y )、f y (x , y )也具有偏导数, 则它们的偏导数称为函数z =f (x , y )的二阶偏导数. 按照对变量求导次序的 不同有下列四个二阶偏导数),()(22y x f x z x z x xx =∂∂=∂∂∂∂,),()(2y x f y x z x z y xy =∂∂∂=∂∂∂∂,),()(2y x f x y z y z x yx =∂∂∂=∂∂∂∂, ),()(22y x f y z y z y yy =∂∂=∂∂∂∂.其中),()(2y x f y x z x z y xy =∂∂∂=∂∂∂∂, ),()(2y x f x y z y z x yx =∂∂∂=∂∂∂∂称为混合偏导数.22)(x z x z x ∂∂=∂∂∂∂, y x z x z y ∂∂∂=∂∂∂∂2)(, x y z y z x ∂∂∂=∂∂∂∂2)(, 22)(y z y z y ∂∂=∂∂∂∂. 同样可得三阶、四阶、以及n 阶偏导数. 二阶及二阶以上的偏导数统称为高阶偏导数.例6 设z =x 3y 2-3xy 3-xy +1, 求22x z ∂∂、33xz ∂∂、x y z ∂∂∂2和y x z ∂∂∂2.解 y y y x xz --=∂∂32233, x xy y x y z --=∂∂2392;2226xy xz =∂∂, 2336yx z =∂∂;196222--=∂∂∂y y x y x z , 196222--=∂∂∂y y x xy z .由例6观察到的问题:yx zx y z ∂∂∂=∂∂∂22定理 如果函数z =f (x , y )的两个二阶混合偏导数x y z ∂∂∂2及yx z ∂∂∂2在区域D 内连续, 那么在该区域内这两个二阶混合偏导数必相等.类似地可定义二元以上函数的高阶偏导数.例7 验证函数22ln y x z +=满足方程02222=∂∂+∂∂y z x z . 证 因为)ln(21ln 2222y x y x z +=+=, 所以22yx x x z +=∂∂, 22y x yy z +=∂∂,222222222222)()(2)(y x x y y x x x y x x z +-=+⋅-+=∂∂,222222222222)()(2)(y x y x y x y y y x y z +-=+⋅-+=∂∂. 因此 0)()(22222222222222=+-++-=∂∂+∂∂y x x y y x y x y z x z . 例8.证明函数r u 1=满足方程0222222=∂∂+∂∂+∂∂z uy u x u , 其中222z y x r ++=.证: 32211r x r x r x r r x u -=⋅-=∂∂⋅-=∂∂, 52343223131r x r x r r x r x u +-=∂∂⋅+-=∂∂. 同理 5232231r y r y u +-=∂∂, 5232231rz r z u +-=∂∂. 因此)31()31()31(523523523222222r z r r y r r x r z u y u x u +-++-++-=∂∂+∂∂+∂∂ 033)(3352352223=+-=+++-=rr r r z y x r .提示: 6236333223)()(rx r rx r r r x x r r x x x u ∂∂⋅--=∂∂⋅--=-∂∂=∂∂.。

高阶偏导数的几何意义
表示固定面上一点的切线斜率。
偏导数f'x(x0,y0)表示固定面上一点对x轴的切线斜率;偏导数f'y(x0,y0)表示固定面上一点对y轴的切线斜率。
高阶偏导数:如果二元函数z=f(x,y)的偏导数f'x(x,y)与f'y(x,y)仍然可导,那么这两个偏导函数的偏导数称为z=f(x,y)的二阶偏导数。
二元函数的二阶偏导数有四个:f"xx,f"xy,f"yx,f"yy。
注意:
f"xy与f"yx的区别在于:前者是先对x求偏导,然后将所得的偏导函数再对y求偏导;后者是先对y求偏导再对x求偏导。
当f"xy与f"yx都连续时,求导的结果与先后次序无关。
在数学中,一个多变量的函数的偏导数,就是它关于其中一个变量的导数而保持其他变量恒定(相对于全导数,在其中所有变量都允许变化)。
偏导数在向量分析和微分几何中是很有用的。



第5节高阶偏导数资料讲解高阶偏导数指的是一个多元函数的某个变量对应的偏导数再次进行偏导数运算的结果,即对偏导数求导。
这是微积分中的一个重要概念,其在数学和工程中都有广泛应用。
一阶偏导数是指函数在该变量处的变化率,二阶偏导数是指函数在该变量处变化率的变化率,以此类推。
具体来说,设函数f(x,y)含有两个自变量x和y,f对x的偏导数为fx,对y的偏导数为fy,则f的二阶偏导数分别为fxx,fyy,以及两个偏导数的混合导数fxy和fyx。
混合导数fxy和fyx并不相等,它们是对同一函数f(x,y)在不同自变量处求偏导数得到的结果。
具体计算方法为先对x求偏导数fx,再对fx关于y进行求偏导数,得到fxy;同理,对y求偏导数fy,再对fy关于x进行求偏导数,得到fyx。
高阶偏导数的计算方法同样可以采用类似的方式:先求出函数的一阶偏导数,然后对一阶偏导数进行求偏导数,即可得到高阶偏导数。
以二阶偏导数为例,设函数f(x,y)的一阶偏导数分别为fx和fy,则f的二阶偏导数fxx,fyy和fxy可以通过以下公式进行计算:fxx = ∂²f / ∂x²这些公式可以进一步推广到高阶偏导数的情况下。
例如,若f的二阶混合导数fxy在一个区域上连续,那么f的二阶偏导数fxx和fyy也存在,且它们相等,即:fxx = ∂²f / ∂x² = ∂/∂x(∂f / ∂x) = ∂/∂x(fx)此外,高阶偏导数具有一些基本性质,如连续性、可交换性和与区间交换极限的等式等。
这些性质为高阶偏导数的计算和应用提供了一定的便利。
总之,高阶偏导数是微积分理论中的重要概念,在许多数学和工程问题中都有广泛的应用。
通过对偏导数的反复求导,我们可以进一步研究函数的性质和变化规律,帮助我们更好地理解和解决实际问题。


5. 高階偏導數;泰勒展開式P1835.1 (4) 計算 xy y x f =),( 的 22x f ¶¶,y x f ¶¶¶2,x y f ¶¶¶2,22y f ¶¶ Hint:)(22x f x xf ¶¶¶¶=¶¶Ans:2)(ln y y x , )1ln (1+-y x y x , )1ln (1+-y x y x ,2)1(--x y x x5.3 )sin ,(cos ),,(q q ==u y x f z r , 說明q q q q 222222222sin sin cos 2cos )(y f y x f x f u u f uf ¶¶+¶¶¶+¶¶=¶¶¶¶º¶¶r r rHint:q q sin cos ),(yf x f u y x f ¶¶+¶¶=¶¶r º),(y x Fq q sin cos ),()(22y F x F u y x F u f u uf ¶¶+¶¶=¶¶=¶¶¶¶=¶¶r r r r 再將代入即可),(y x FP1845.4 (5) 如果),(y x f 滿足2222yf x f ¶¶+¶¶=0則稱為諧和函數. 檢驗)ln(),(22y x y x f +=是否為諧和函數Hint:)ln(21),(22y x y x f += , 22y x y x f +=¶¶ , 2222222)(y x x y x f +-=¶¶=-22yf ¶¶Ans: 是P1875.8 (1) 求 32233),(y xy y x x y x f +-+= 在(1,2)展開的三階泰勒多項式 Hint:f x =3x 2+2xy-3y 2f y =x 2-6xy+3y 2f xx =6x+2yf xy =2x-6yf yy =-6x+6yf xxx =6f xxy =2f xyy =-6f yyy =6 再將點(1,2)代入三階泰勒展式即可Ans:-1+[-5(x-1)-2(y-2) ] +21[10(x-1)2-20(x-1)(y-2)+6(y-2)2]+ !31[6(x-1)3+6(x-1)2(y-2)-18(x-1)(y-2)2+6(y-2)3)]5.9 利用單變數的泰勒展開式,先猜猜看下述函數在指定點的泰勒展式,再驗算之至第三階(3) )0,0(,cos sin y x (6) )0,0(,122y x ++Hint: (3) )!4!21)(!5!3(4253L L ++-++-y y x x x (6) L +++!2122y xAns: (3) L +--!3!232x xy x (6) L +++)(!21122y x6. 極值測試與應用P1906.2 找出下列函數的候選點,決定其極值性質(即使D=0)(4) )(22y xxe +-Hint: )(22),(y x xe y x f +-=, 候選點滿足0)21(2)(22=-=¶¶+-x e x f y x 且 0)2()(22=-=¶¶+-xy e yf y xAns: (0,21) 極大值 (0,21-) 極小值6.3 (4) 討論R y xy x y x f Î++=l l ,),(22 依不同l 值,討論其候選點及極值性質Hint:候選點滿足 02=+=¶¶y x x f l 且 02=+=¶¶y x yf l 再利用定理6.2判別,考慮úûùêëé22l lAns:l >2時,(0,0)為鞍點。


