第8讲-高阶偏导数与极值
- 格式:doc
- 大小:303.00 KB
- 文档页数:4

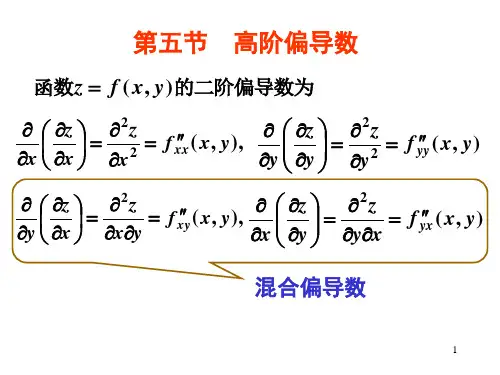



高阶偏导数韩桂玲教学目标: 1.掌握二元函数的二阶偏导数及高阶偏导数的定义2.会求二元函数的二阶偏导数3..理解二阶连续混合偏导数相等的定理证明教学重点: 1.掌握二元函数的二阶偏导数及高阶偏导数的定义2.会恰当的用定义法和公式法求二元函数的二阶及高阶偏导数教学难点: 二阶连续混合偏导数相等的定理证明教学方法: 讲授法教学过程:引入:若二元函数),(y x f z =在区域D 存在x 与y 的一阶偏导数,对D y x ∈∀),(xy x f y x x f y x f x z x x ∆-∆+='=∂∂→∆),(),(lim ),(0 (把y 看作常数) yy x f y y x f y x f y z y y ∆-∆+='=∂∂→∆),(),(lim ),(0 (把x 看作常数) 1.二阶偏导数定义若二元函数),(y x f z =在区域D 存在x 与y 的(一阶)偏导数),(y x f xz x '=∂∂与),(y x f y z y '=∂∂则在D 内它们都是x 与y 的二元函数。
若它们关于x 与y 的偏导数存在,即),()(22y x f xz x z x xx ''=∂∂=∂∂∂∂x y x f y x x f x x x ∆'-∆+'=→∆),(),(lim 0 (把y 看作常数) 定义法表出 ),()(2y x f y x z x z y xy ''=∂∂∂=∂∂∂∂yy x f y y x f x x y ∆'-∆+'=→∆),(),(lim 0 (把x 看作常数) 定义法表出 ),()(2y x f x y z y z x yx ''=∂∂∂=∂∂∂∂xy x f y x x f y y x ∆'-∆+'=→∆),(),(lim 0(把y 看作常数) 定义法表出 ),()(22y x f yz y z y yy ''=∂∂=∂∂∂∂y y x f y y x f y y y ∆'-∆+'=→∆),(),(lim 0(把x 看作常数) 定义法表出 则称它们是二元函数),(y x f z =的二阶偏导数,其中第二、三个二阶偏导数称为混合偏导数。






极值和最值的高阶导数在微积分学中,极值和最值是非常常见的概念。
它们在实际问题中的应用也非常广泛。
在求解极值与最值问题时,常用的方法就是求解函数的一阶和二阶导数。
不过,有的时候我们需要求解的不仅仅是函数的一阶和二阶导数,而需要求解更高阶的导数。
本文将介绍关于极值和最值的高阶导数的相关知识。
一、函数的高阶导数首先,我们需要回顾一下函数的高阶导数的定义。
对于一个导数存在的函数 $f(x)$,它的 $n$ 阶导数定义如下:$$f^{(n)}(x)=\frac{\mathrm{d}^n}{\mathrm{d}x^n}f(x)$$其中,$n$ 表示求导的次数。
对于高阶导数,我们同样可以利用导数的定义,将其表示成极限的形式:$$f^{(n)}(x)=\lim_{h\rightarrow 0}\frac{f^{(n-1)}(x+h)-f^{(n-1)}(x)}{h}$$这个式子表示的是函数 $f(x)$ 的 $n$ 阶导数。
我们可以利用这个式子依次求解函数的一阶、二阶、三阶……直到 $n$ 阶导数。
二、极值和最值的定义在讲述高阶导数之前,我们先来回忆一下极值和最值的定义。
先定义一下局部极大值、局部极小值、全局极大值和全局极小值:局部极大值:对于函数 $f(x)$,若存在$x_0\in\operatorname{Dom}(f)$,使得对于 $\epsilon>0$,有$f(x_0)>f(x)$ 对于任意的 $x\in(x_0-\epsilon,x_0+\epsilon)\cap\operatorname{Dom}(f)$ 成立,则称$x_0$ 为函数 $f(x)$ 的一个局部极大值。
局部极小值:对于函数 $f(x)$,若存在$x_0\in\operatorname{Dom}(f)$,使得对于 $\epsilon>0$,有$f(x_0)<f(x)$ 对于任意的 $x\in(x_0-\epsilon,x_0+\epsilon)\cap\operatorname{Dom}(f)$ 成立,则称$x_0$ 为函数 $f(x)$ 的一个局部极小值。
第8讲 高阶导数与二元函数极值讲授内容一、高阶偏导数由于),(y x f z =的偏导函数),(),,(y x f y x f y x 仍然是自变量x 与y 的函数,如果它们关于x 与y 的偏导数也存在,则说函数f 具有二阶偏导数,二元函数的二阶偏导数有如下四种情形:),(22y x f x z x xz xx =⎪⎭⎫⎝⎛∂∂∂∂=∂∂, ).,(22y x f y z y y z yy =⎪⎪⎭⎫⎝⎛∂∂∂∂=∂∂ ),,(2y x f x z y y x zxy =⎪⎭⎫⎝⎛∂∂∂∂=∂∂∂ ),(2y x f y z x x y z yx=⎪⎪⎭⎫⎝⎛∂∂∂∂=∂∂∂例1 求函数xy z arctan=的所有二阶偏导数. 解:()22222222y x xyyx yx xz +=⎪⎪⎭⎫ ⎝⎛+-∂∂=∂∂, ().22222222y x xyy x x y yz +-=⎪⎪⎭⎫ ⎝⎛+∂∂=∂∂(),22222222y x y x yx yy y x z+--=⎪⎪⎭⎫ ⎝⎛+-∂∂=∂∂∂ (),22222222y x y x y x x x x y z +--=⎪⎪⎭⎫ ⎝⎛+∂∂=∂∂∂注意:从上面例子看到, 关于x 和y 的不同顺序的两个二阶偏导数都相等(称为混合偏导数),但这个结论并不对任何函数都成立(见例2).例2 设函数()⎪⎩⎪⎨⎧=+≠++-=.0 ,0,0 ,,22222222y x y x y x y x xy y x f解: 它的一阶偏导数为()()()()()⎪⎩⎪⎨⎧=+≠++++-=,0 ,0,0 ,4,2222222222222y x y x yx y x y y x y x y y x f x ()()()()()⎪⎩⎪⎨⎧=+≠++-+-=,0 ,0,0 ,4,2222222222222y x y x yx y x x y x y x x y x f y 进而求f 在(0,0)处的混合偏导数,得 ()()(),1lim0,0,0lim0,00-=∆∆-=∆-∆=→∆→∆yy yf y f f y x x y xy ()()()1lim0,00,lim0,00=∆∆=∆-∆=→∆→∆xx xf x f f x y y x yx .由此看到,这里的()y x f ,在原点处的两个二阶混合偏导数与求导顺序有关,那么,在什么条件下混合偏导数与求导顺序无关呢?定理17.7 若),(),(y x f y x f yx xy 和都在点),(00y x 连续,则()()0000,,y x f y x f yx xy = .这个定理的结论对n 元函数的混合偏导数也成立。
如三元函数),,(z y x f u =,若下述六个三阶混合偏导数),,(),,,(),,,(),,,(),,,(),,,(z y x f z y x f z y x f z y x f z y x f z y x f zyx yxz xzy zxy yzx xyz 在某一点都连续,则在这一点六个混合偏导数都相等.例3 1)设,,⎪⎪⎭⎫ ⎝⎛=y x x f z 求22x z ∂∂,.2y x z ∂∂∂ 2)设(),,y x xy f z -= 求22x z∂∂,.2y x z ∂∂∂ 解:这里z 是以x 和y 为自变量的复合函数,它也可以改写成如下形式:.,),,(yx v x u v u f z ===由复合函数求导公式有.1vf y uf xv v f xu u f xz ∂∂+∂∂=∂∂∂∂+∂∂∂∂=∂∂注意,这里vfu f∂∂∂∂,仍是以v u ,为中间变量y x ,为自变量的复合函数.所以⎪⎪⎭⎫ ⎝⎛∂∂+∂∂∂∂=∂∂v f y u f x x1z22⎪⎪⎭⎫ ⎝⎛∂∂∂∂+∂∂∂∂∂+∂∂∂∂∂+∂∂∂∂=x v v f x u u v f y x v v u f x u u f 2222221,12222222v fy v u f y u f ∂∂+∂∂∂+∂∂= ⎪⎪⎭⎫⎝⎛∂∂+∂∂∂∂=∂∂∂v f y u f y y x z12⎪⎪⎭⎫ ⎝⎛∂∂∂∂+∂∂∂∂∂+∂∂-∂∂∂∂∂+∂∂∂∂=y v v f y u u v f y v f y y v v u f y u u f 222222211 .1222322vf yvf yx vu f y x ∂∂-∂∂-∂∂∂-=二、中值定理先介绍凸区域的概念.若区域D 上任意两点的连线都含于D ,则称D 为凸区域.这就是说对任意两点D y x P y x P ∈),(),,(222111和一切),10(≤≤λλ,恒有.))(),((121121D y y y x x x P ∈-+-+λλ定理17.8(中值定理) 设二元函数f 在凸开域2R D ⊂上连续,在D 的所有点内都可微,则对D 内任意两点,int ),(),,(D k b h a Q b a P ∈++,存在某),10(<<θθ,使得.),(),(),(),(k k b h a f h k b h a f b a f k b h a f y x θθθθ+++++=-++证:令 ).,()(tk b th a f t ++=Φ它是定义在[]1,0上的一元函数,由定理中的条件知()t Φ在[]1,0上连续,在()1,0内可微.于是根据一元函数中值定理,存在)10(<<θθ使得 ).(')0()1(θΦ=Φ-Φ 由复合函数的求导法则.),(),()('k k b h a f h k b h a f y x θθθθθ+++++=Φ定理17.9(泰勒定理) 若函数f 在点),(000y x P 的某邻域)(0P U 内有直到1+n 阶的连续偏导数,则对)(0P U 内任一点),(00k y h x ++,存在相应的)1,0(∈θ,使得 +∂∂+∂∂+=++),()(),(),(000000y x f ykx h y x f k y h x f ++∂∂+∂∂ ),()(!21002y x f ykx h+∂∂+∂∂),()(!100y x f ykxh n n()).,()(!11001k y h x f ykxh n n θθ++∂∂+∂∂++ 称为二元函数f 在点0P 的n 阶泰勒公式,其中.),(),()(00000im i im im mi i mmkh y x f yx Cy x f ykxh--=∂∂∂=∂∂+∂∂∑例4 求yx y x f =),(在点(1,4)的泰勒公式(到二阶为止). 解:由于,2,4,100===n y x ,因此有().0)4,1(,ln ),(.1)4,1(,ln ),(,12)4,1(,)1(),(,0)4,1(,ln ),(,4)4,1(,),(,1)4,1(,),(222221121===+==-=======----y yy xy y y xy x y x y yy x y x yf x xy x f f x yxxy x f f xy y y x f f x x y x f f yxy x f f x y x f将它们代入泰勒公式,即得().)4)(1()1(6)1(4122ρo y x x x x y+--+-+-+=三、极值问题定义 设函数f 在点()000,y x P 的某邻域)(0P U 内有定义.若对于任何点()()0,P U y x P ∈成立不等式()(),或)()()(00P f P f P f P f ≥≤则称函数f 在点0P 取得极大(或极小)值,点0P 称为f 的极大(或极小)值点.极大值、极小值统称极值.极大值点、极小值点统称极值点.由定义可见,若f 在点()00,y x 取得极值,则当固定0y y =时,一元函数()0,y x f 必定0x x =在取相同的极值上.同理,一元函数()y x f ,0在0y y =也取相同的极值.于是得到二元函数取极值的必要条件如下: 定理17.10(极值必要条件) 若函数f 在点()000,y x P 存在偏导数,且在0P 取得极值,则有 ()().0,,0,0000==y x f y x f y x反之,若函数f 在点0P 满足()()0,,0,0000==y x f y x f y x ,则称点0P 为f 的稳定点.定理17.10指出:若f 存在偏导数,则其极值点必是稳定点。
但稳定点并不都是极值点,如例函数xy y x h =),(,原点为为其稳定点,但它在原点并不取得极值.与一元函数的情形相同,函数在偏导数不存在的点上也有可能取得极值。
例如22),(y x y x f +=在原点没有偏导数,但0)0,0(=f 是f 的极小值.定理17.11(极值充分条件) 设二元函数f 在点),(000y x P 的某邻域)(0P U 内具有二阶连续导数,且0P 是f 的稳定点. 则有(ⅰ)当()()0)(,0020>->P f f f P f xy yy xx xx 时,f 在点0P 取得极小值;(ⅱ)当()()0)(,0020>-<P f f f P f xy yy xx xx 时,f 在点0P 取得极大值;(ⅲ)当()0)(02<-P f f f xy yy xx 时,f 在点0P 不能取得极值;(ⅳ)当()0)(02=-P f f f xy yy xx 时,不能肯定f 在点0P 是否取得极值.例5 求61065),(22++-+=y x y x y x f 的极值.解: 由方程组 ⎩⎨⎧=+==-=01010,062y f x f yx 得f 的稳定点()1,30-P ,由于()()()().20)(,10,0,202000=-===P f f f P f P f P f xy yy xx yy xy xx 因此f 在点0P 取得极小值.8)1,3(-=-f 又因f 处处存在偏导数,故)1,3(-为f 的惟一极值点.例6 讨论xy x y x f +=2),(是否存在极值.解:由方程组0,02===+=x f y x f y x ,得稳定点为原点)0,0(.因,012<-=-xy yy xx f f f ,故原点不是f 的极值点。
又因f 处处可微,所以f 没有极值点。