高阶偏导数

第5节高阶偏导数

x x
x 2 z
2z x 2
(2 z) x z x
(2 z)2
(2 z) x x 2 z
(2 z)2
(2
z)2 (2 z)3
x2
.
7
例6 已知 u eu xy ，求 2u ， xy
解设 F ( x, y, z) u eu xy ，
Fx y , Fy x , Fu 1 eu ,
y0 )表示
h2 f xx (x0 , y0 ) 2hk f x y (x0 , y0 ) k 2 f y y (x0 , y0 )
•
一般地,(h k )m x y
f (x0 ,
y0 ) 表示
m
Cmp
p0
h
pk
m
p
x
m f p ym
p
(x0 ,
y0 )
定理1. 设 z f (x, y) 在点(x0, y0 ) 的某一邻域内有直
6x2
y
9 y2
1.
2
例2 设 u eax cos by ，求二阶偏导数.
解 u aeax cosby , u beax sinby ;
x
y
2u x 2
a 2eax
cos
by
,
2u y 2
b2eax
cos by
,
2u abeax sinby , 2u abeax sinby .
xy
yx
一般地,若 2z 与 2z 是连续函数,则必相等. xy yx
a2 ( x
ay)
a 2
( x
ay)
a2
2u x 2
.
4
例4 证明函数 u ln x2 y2 z2 满足方程

09-4_高阶偏导数

z f xx f11 2 x
2
2 z f xy f12 xy
z f yy f 22 2 y
2
z f yx f 21 yx
2
二元函数的二阶偏导数共 22 = 4 项
例
二元函数 z f ( x, y ) 的三阶偏导数：
2
z y
x
y
z z 2 x x x
z z y x xy
2
2z z x y yx
z 2 z 2 y y y
高阶偏导数还可使用下列记号
发现求高阶导数与求导顺序有关.
例
解
3 2 3 求 z x y 3xy xy 1 的二阶偏导数.
先求一阶偏导数：
z 3x 2 y 2 3 y 3 y, x
z 2 x 3 y 9 xy 2 x, y
x y
再求二阶偏导数：
z x
z y
x y
2 z z 2 (3x 2 y 2 3 y 3 y ) 6xy x 2 x x x
1
2z 2z yx xy 2z y 2
2z x 2
x y
2 z x 2
2 z 3 z 2 3 x x x
2 z 3 z 2 2 y x x y
例
二元函数 z f ( x, y ) 的三阶偏导数：
3
2z 2z yx xy 2z y 2
2z x 2
x y
2z xy
2 z 3 z x xy xyx 2 z 3 z y xy xy 2

一偏导数定义及其计算法二高阶偏导数三小结

思考题解答
不能. 例如, f ( x, y) x2 y2 , 在(0, 0)处连续, 但 f x (0, 0) f y (0, 0) 不存在.
，
f y
，
z
y
或
f y(x, y).
偏导数的概念可以推广到二元以上函数
例如，u f ( x, y,z), 在 ( x, y,z) 处，
f
x
(
x
,
y,
z
)
lim
x0
f
( x x, y,z) x
f
(x, y,z) ,
f
y
(
x,
y,z
)
lim
y0
f
( x, yy,z) y
f
(x, y,z)
,
f
z
(
x,
y,z)
y( y2 x2) ( x2 y2 )2
,
考虑点 (0, 0) 对 x 的偏导数，
lim
x0
f (0 x, 0) x
f (0, 0)
lim
x0
00 x
0.
于是，
f
x
(
x
,
y
)
y( (x
y
2
2 x2) y2 )2
,
0,
x2 y2 0, x2 y2 0.
(2) 求 f y ( x, y). 当 x2 y2 0 时，即 x 0 且 y 0时，
如图
z f ( x0, y)
M0 Tx
z f ( x, y0 )
Ty
几何意义:
偏导数 f x ( x0, y0 )就是曲面被平面 y y0 所截得的曲线在点 M0处的切线 M0Tx对 x轴的斜率.

多元函数的偏导数与方向导数计算

多元函数的偏导数与方向导数计算在多元函数中，偏导数与方向导数是常用的求导工具，可以帮助我们研究函数在不同方向上的变化率和导数值。

本文将介绍计算多元函数的偏导数和方向导数的方法和公式，并通过实例进行说明。

一、多元函数的偏导数多元函数是指含有多个自变量的函数，其偏导数表示在各个自变量上的变化率。

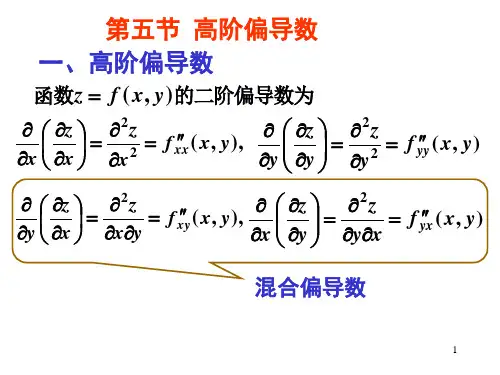
1. 一阶偏导数对于二元函数 $z = f(x, y)$，其一阶偏导数表示对每个自变量的偏导数值。

分别记作 $\frac{{\partial z}}{{\partial x}}$ 和 $\frac{{\partial z}}{{\partial y}}$，计算方法如下：$$\frac{{\partial z}}{{\partial x}} = \lim_{{\Delta x \to 0}} \frac{{f(x + \Delta x, y) - f(x, y)}}{{\Delta x}}$$$$\frac{{\partial z}}{{\partial y}} = \lim_{{\Delta y \to 0}} \frac{{f(x, y + \Delta y) - f(x, y)}}{{\Delta y}}$$2. 高阶偏导数如果一阶偏导数存在，我们还可以继续求解二阶、三阶乃至更高阶的偏导数。

对于二阶偏导数，我们可以通过对一阶偏导数再次求导得到，记作 $\frac{{\partial^2 z}}{{\partial x^2}}$、$\frac{{\partial^2 z}}{{\partial x \partial y}}$ 和 $\frac{{\partial^2 z}}{{\partial y^2}}$。

计算方法如下：$$\frac{{\partial^2 z}}{{\partial x^2}} = \frac{{\partial}}{{\partial x}} \left(\frac{{\partial z}}{{\partial x}}\right)$$$$\frac{{\partial^2 z}}{{\partial x \partial y}} =\frac{{\partial}}{{\partial x}} \left(\frac{{\partial z}}{{\partial y}}\right)$$$$\frac{{\partial^2 z}}{{\partial y^2}} = \frac{{\partial}}{{\partial y}} \left(\frac{{\partial z}}{{\partial y}}\right)$$二、多元函数的方向导数方向导数表示函数在某个方向上的变化率，是由函数的梯度（gradient）来表示的。

第5节高阶偏导数资料讲解

第5节高阶偏导数资料讲解高阶偏导数指的是一个多元函数的某个变量对应的偏导数再次进行偏导数运算的结果，即对偏导数求导。

这是微积分中的一个重要概念，其在数学和工程中都有广泛应用。

一阶偏导数是指函数在该变量处的变化率，二阶偏导数是指函数在该变量处变化率的变化率，以此类推。

具体来说，设函数f(x,y)含有两个自变量x和y，f对x的偏导数为fx，对y的偏导数为fy，则f的二阶偏导数分别为fxx，fyy，以及两个偏导数的混合导数fxy和fyx。

混合导数fxy和fyx并不相等，它们是对同一函数f(x,y)在不同自变量处求偏导数得到的结果。

具体计算方法为先对x求偏导数fx，再对fx关于y进行求偏导数，得到fxy；同理，对y求偏导数fy，再对fy关于x进行求偏导数，得到fyx。

高阶偏导数的计算方法同样可以采用类似的方式：先求出函数的一阶偏导数，然后对一阶偏导数进行求偏导数，即可得到高阶偏导数。

以二阶偏导数为例，设函数f(x,y)的一阶偏导数分别为fx和fy，则f的二阶偏导数fxx，fyy和fxy可以通过以下公式进行计算：fxx = ∂²f / ∂x²这些公式可以进一步推广到高阶偏导数的情况下。

例如，若f的二阶混合导数fxy在一个区域上连续，那么f的二阶偏导数fxx和fyy也存在，且它们相等，即：fxx = ∂²f / ∂x² = ∂/∂x(∂f / ∂x) = ∂/∂x(fx)此外，高阶偏导数具有一些基本性质，如连续性、可交换性和与区间交换极限的等式等。

这些性质为高阶偏导数的计算和应用提供了一定的便利。

总之，高阶偏导数是微积分理论中的重要概念，在许多数学和工程问题中都有广泛的应用。

通过对偏导数的反复求导，我们可以进一步研究函数的性质和变化规律，帮助我们更好地理解和解决实际问题。

第五节高阶偏导数

′′ f 22
二元函数的二阶偏导数共 22 = 4 项
二元函数 z = f ( x , y ) 三阶偏导数
∂ z 2 ∂x
2
x
y
∂ ∂ 2z ∂ 3z 2= 3 ∂x ∂x ∂x
∂3z ∂ ∂ 2z 2= 2 ∂y ∂x ∂x ∂y ∂ ∂2z ∂3z 2= 2 ∂ x ∂ y ∂ y ∂x
3x y( x + y ) − x y ⋅ 2x ′ f x ( x, y) = 2 2 2 (x + y )
2 2 2 3
3x y( x + y ) − x y ⋅ 2x ′ f x ( x, y) = 2 2 2 (x + y )
2 2 2 3
3x y 2x y , = 2 − 2 2 2 2 x + y (x + y )
x 2x y ′ f y ( x, y) = 2 , − 2 2 2 2 x + y (x + y )
3 3 2
2
4
当 ( x , y ) = (0,0) 时,
0 f (∆x,0) − f (0,0) = lim = 0, ′ f x (0,0) = lim ∆x→0 ∆x ∆x→0 ∆x f (0, ∆y) − f (0,0) 0 ′ f y (0,0) = lim = lim = 0, ∆y→0 ∆y ∆y→0 ∆y
∂z Fx′ 故 = − =− ∂x Fz′
Fy′ ∂z =− ∂y Fz′
z = x+z x+z − 2 1 z 2 z y =− x+z = y( x + z ) − 2 z
∂z ∂z ( x + z) − z 2 z ∂ ∂ z ∂y ( ) = ∂y = ∂y x + z ∂ x∂ y ( x + z )2 z′y =

∂z . 的二阶偏导数及 2 ∂y∂x ∂z = 2ex+2y ∂y ∂2 z x+2y = 2e ∂x∂y
3
例12.1.11
f (x, y) =
x2 − y2 xy 2 , x2 + y2 ≠ 0 x + y2 0, x2 + y2 = 0
f x (x, y) =
x4 + 4x2 y2 − y4 y , x2 + y2 ≠ 0 (x2 + y2 )2
证: 记 ϕ ( x ) = f ( x , y0 + ∆y ) − f ( x , y0 ),
ψ ( y ) = f ( x0 + ∆x , y ) − f ( x0 , y ),
f ( x 0 + ∆ x , y 0 + ∆y ) − f ( x 0 , y 0 + ∆y ) − f ( x 0 + ∆x , y 0 ) + f ( x 0 , y 0 ) I= . ∆ x∆ y
(与求导顺序无关时, 应选择方便的求导顺序)
下页结束
练习题：练习题：设
确定 u 是 x , y 的函数 , 连续, 且解: 求
方程
首页
上页
返回
下页
结束
练习题
一、填空题: 填空题: 1 、设 z = ln tan
x ∂z ∂z ,则 = ________; = _________. ∂x y ∂y ∂z ∂z 2 、设 z = e xy ( x + y ), 则 = _______; = ________. ∂x ∂y y ∂u ∂u 3 、设 u = x z , 则 = __________; = __________; ∂x ∂y ∂u = ____________. ∂z ∂2z y ∂2z 4 、设 z = arctan , 则 2 = ________; 2 = _______; x ∂x ∂y ∂2z = ____________. ∂x∂y

高阶导数与高阶偏导数

f (n)( x),
y(n),
dny dx n
或
d
n f (x) dx n
.
二阶和二阶以上的导数统称为高阶导数.
相应地, f ( x)称为零阶导数; f ( x)称为一阶导数.
湘潭大学数学与计算科
3
学学院
例1 已知函数 y ( x3 7 x 8)20(3x 7)30 求 y(90)和 y(91) .
(2) (Cu)(n) Cu(n)
(3) (u v)(n) u(n)v nu(n1)v n(n 1) u(n2)v 2!
n(n 1)(n k 1) u v (nk ) (k ) uv (n) k!
n
C u v k (nk ) (k ) n
莱布尼兹公式
湘潭大学数学与计算科
14
斯方程
2u x 2
2u y2
0.
解因为 ln x2 y2 1 ln( x2 y2 ),
2
湘潭大学数学与计算科
11
学学院
因此
u x x x2 y2 ,
u y
x2
y
y2
,
2u x 2
(x2 y2) x 2x ( x2 y2 )2
y2 x2 ( x2 y2 )2
,
2u (x2 y2) y 2 y y2 ( x2 y2 )2
解由于函数
y ( x3 7 x 8)20(3x 7)30
展开后的最高次幂项为
所以
330 x32030 330 x90
y(90) 330 90!, y(91) 0.
湘潭大学数学与计算科
4
学学院
一、高阶偏导数的定义
函数z f ( x, y)的二阶偏导数为

高阶偏导数及泰勒公式

z(x,
y)由方程 x 2
y 2
tgz
e 所确定, z
求
x 2
z 2
.
解: (1) 记F (x, y, z) x2 y2 tgz ez
由隐函数求导公式 z Fx , x Fz
有Fx 2x, Fz sec2 z ez .
从而,
z x
ez
2x sec2
z
z
2x
x ez sec2 z
y)
f x( x,
y) y
lim
y0
f x( x,
y
y) y
f x( x,
y) ,
lim
y0
1 y
lxim0
f
(x
x,
y
y) x
f
(x,
y
y)
lim x0
f
(x
x, y) x
f
(x,
y)
lim lim 1 1 f (x x, y y) f (x, y y)
y0 x0 y x
f (x x, y) f (x, y)
一般,若z f (x, y)的k 1阶微分dk1z存在,且仍可微. 则记dk z d(dk1z),称为z的k阶微分.
下边推导 z 的 k 阶微分的计算公式. 设以 x, y 为自变量的函数 z = f (x, y)Ck .
有 dz fx(x, y)dx f y(x, y)dy 由于x, y 为自变量,故dx = x, dy = y,与 x, y 的取值无关. 固定x, y,, (即将它们看作常数), 求dz的微分. 易见,当f x, f y存在连续偏导时, dz可微.即, 若f C 2 ,则z f (x, y)存在二阶微分(二阶可微).

高阶导数与高阶偏导数

高阶导数可以描述曲线的弯曲程度，例如二阶导数表示曲线的凹凸程度，三阶导数表示曲线的拐点变化趋势。
03
高阶偏导数
高阶偏导数的定义
总结词
高阶偏导数是函数在某一点的各阶偏导数。
详细描述
高阶偏导数是指函数在某一点的各阶偏导数。对于一个多元函数，在某一点处的偏导数表示该函数在该点的切线斜率。高阶偏导数则表示该切线的弯曲程度，即函数在该点的各阶偏导数。
二阶及以上的导数和偏导数可以描述函数图像的凹凸性和拐点等几何特性。
偏导数表示函数图像上某一点处沿某一方向的变化率。
02
高阶导数
高阶导数的定义
定义
高阶导数是函数在某一点的导数的导数，即函数在这一点连续可导的情况下，求导数的过程可以反复进行，得到的极限值称为高阶导数。
表示方法
对于一元函数，高阶导数表示为f^(n)(x)，其中n表示求导的次数；对于多元函数，高阶偏导数表示为 ∂^n/∂x_1∂x_2...∂x_n。
高阶导数与高阶偏导数
目录
• 导数与偏导数的定义 • 高阶导数 • 高阶偏导数 • 导数与偏导数的应用 • 高阶导数与高阶偏导数的应用
01
导数与偏导数的定义
导数的定义
函数在某一点的导数描述了函数在该点的切线斜率。
导数是函数值随自变量变化的速率，即函数在某一点的切线斜率。
导数公式：$f'(x) = lim_{Delta x to 0} frac{Delta y}{Delta x}$
高阶导数可以用于分析函数的局部形态和性质，如拐源自、极值点、凹凸性等。详细描述
通过求取函数的高阶导数，可以判断函数的单调性、凹凸性以及拐点，从而更深入地了解函数的形态和性质。
总结词

7.5高阶偏导数与高阶全微分

′′ ′′ ′′ ′′ = ( f xx dx + f yx dy )dx + ( f xy dx + f yy dy )dy
2 2
′′ ′′ ′′ = f xx (dx) + 2 f xy dxdy + f yy (dy )
习惯上记(dx) = dx , (dy ) = dy
2 2 2 2
′′ ′′ ′′ ∴ d 2 z = f xx dx 2 + 2 f xy dxdy + f yy dy 2
∂z ∂f ∂u ∂f ∂v ∂u ∂v = • + • = f1′ + f 2′ = yf1′+ 2 xf 2′ ∂x ∂u ∂x ∂v ∂x ∂x ∂x
其中f1′, f 2′是关于u , v的函数
∂f1′ ∂u ∂f1′ ∂v Q ( yf1′)′x = y ( f1′)′x = y • + • ∂u ∂x ∂v ∂x
dx + 2dy + dz = e
x− y − z
(dx − dy − dz )
= ( x + 2 y + z )(dx − dy − dz )
x + 2 y + z −1 x + 2y + z + 2 ∴ dz = dx − dy 1+ x + 2 y + z 1+ x + 2 y + z
∂z x + 2 y + z − 1 2 ∴ = = 1− ∂x 1 + x + 2 y + z 1+ x + 2 y + z
′′ ′′ ′′ ′′ = f1′+ xyf11 − y f12 + 2 x f 21 − 4 xyf 22

高阶偏导数、方向导数与梯度PPT课件

有
而初等说明: 因为初等函数的偏导数仍为初等函数 ,
函数在其定义区域内是连续的 , 故求初等函数的高阶导数可以选择方便的求导顺序. (与求导次序无关. )
7/30
二、方向导数
f ( x, y, z ) 在点 P( x, y, z ) 处定义: 若函数
沿方向
0
l
, , ) 存在下列极 l (方向角为
6/30
r2
定理. 若 f x y ( x,y) 和 f y x ( x,y) 都在点 ( x0 ) f y x ( x0 , y0 )
(证明在P29-30)
本定理对 n 元函数的高阶混合导数也成立. 例如, 对三元函数 u = f (x , 当三阶混合偏导数 y , (z 在点 x) ,, y , z) 连续时,
n
3/3
3 例1. 求函 z x2y . ze 的二阶偏导数及 2 数 y x z z 解 : 2 e x2y e x2y y x
z x2y e 2 x 2 2 z z x2y x2y 4e 2e 2 y x y 3 2 z z x2y ( ) 2 e y x 2 x y x 2z 2z , 但这一结论并不总成立. 注意:此处 x y y x
导数: z 2z z 2 z ( ) f x y ( x, y ) ( ) 2 f x x ( x, y ); y x y x x x x
2 z z ( ) f y x ( x, y) f 21 ( x, y); x y x y 2 z z ( ) f y y ( x, y) f 22 ( x, y) 2 y y y
5/30

高阶偏导数与高阶全微分

2 f2 y2 f11 4xyf12 4x2 f22 ,
2z xy
f1
y
f11
u y
f
22
v y
2
x
fy[ xf11 2 yf12 ] 2x[ xf21 2 yf22]
f1 xyf11 2( x2 y2 ) f12 4xyf22 .
例3 设由方程 x 2 y z e x yz 确定的隐函数为 z z(x, y), 求 2z .
2
,
x 1 x 2 y z 1 x 2 y z
z x 2 y z 2 1
1
.
y 1 x 2 y z
1 x2y z
从而
2z xy
(1
2 2 z y x2y
z)2
2( x 2 y z) (1 x 2 y z)3
.
二、高阶全微分
考虑 z f (x, y) 的全微分 dz f x( x, y)dx f y( x, y)dy
xy 解方程 x 2 y z ex yz 两边求全微分, 得
dx 2dy dz ex yz (dx dy dz)
因此
( x 2 y z)(dx dy dz)
dz x 2 y z 1dx x 2 y z 2dy 1 x2y z 1 x2y z
由此可得
z x 2 y z 1 1
[1
2x3 y ( xy)2
]2
d2z zxxdx2 2zxydxdy zyydy2
[1
1 ( xy)2
]2
[2
xy 3dx 2
2(1
x2
y2
)dxdy
2
x3
ydy
2
].
三、二元函数的泰勒公式

一偏导数的定义及其计算法二高阶偏导数三小结

偏导数都存在，那么这个偏导数就是 x、 y的函数，
它就称为函数z f (x, y)对自变量 x的偏导数，记作
z x
，
f x
，
z
x
或
fx(x, y).
同理可定义函数z f ( x, y)对自变量 y的偏导数，记作
z y
，
f y
，
z
y
或
f y(x, y).
偏导数的概念可以推广到二元以上函数
例如，u f ( x, y,z), 在 ( x, y,z) 处，
2z
xy
3x2y2 3y3 y
y
6x2 y 9 y2 1,
2z
yx
2 x3
y
9 xy 2
x
x
6x2 y 9 y2 1.
2z
y2
2x3 y 9xy2
x
y
2x3 18 xy;
3z
x 3
6 xy 2
x
6y2,
例 9 设u eax cos by ，求二阶偏导数.
解
,
考虑点 (0, 0) 对 x 的偏导数，
lim
x0
f (0 x, 0) x
f (0, 0)
lim
x0
00 x
0.
于是，
f
x
(
x
,
y
)
y( (x
y
2
2 x2) y2 )2
,
0,
x2 y2 0, x2 y2 0.
(2) 求 f y ( x, y). 当 x2 y2 0 时，即 x 0 且 y 0时，
0,
x2 y2 0
求 f x ( x, y), f y ( x, y).

高阶偏导数先代后求

高阶偏导数先代后求【原创实用版】目录1.高阶偏导数的概念2.高阶偏导数与普通函数的导数的区别3.高阶偏导数的求解方法4.高阶偏导数在实际问题中的应用5.总结正文一、高阶偏导数的概念在数学中，高阶偏导数是指一个多元函数的偏导数，它是关于其中一个变量的导数，而保持其他变量恒定。

偏导数在向量分析和微分几何中很有用。

高阶偏导数是针对函数的一个自变量求多次导数，而偏导数是针对多自变量的函数中的一个自变量进行求导。

二、高阶偏导数与普通函数的导数的区别普通函数的导数涉及到所有自变量的变化，因此不能先代后算。

如果先代后算，可能会导致结果不准确。

而在计算高阶偏导数时，可以先代后算。

这是因为高阶偏导数是针对一个自变量进行求导，与其他自变量无关。

三、高阶偏导数的求解方法求高阶偏导数的方法与求普通函数的导数类似，只不过需要对一个自变量进行多次求导。

在求解高阶偏导数时，需要注意保持其他变量的恒定。

例如，对于函数 f(x, y)，求关于 x 的二阶偏导数，可以先对 y 求一次导数，然后再对 x 求一次导数。

四、高阶偏导数在实际问题中的应用高阶偏导数在实际问题中的应用非常广泛，例如在物理学、工程学和经济学等领域。

在物理学中，高阶偏导数可以用来描述物体的振动和波动；在工程学中，高阶偏导数可以用来分析结构的稳定性和强度；在经济学中，高阶偏导数可以用来研究经济系统的稳定性和动态行为。

五、总结高阶偏导数是一种重要的数学概念，它在向量分析和微分几何中具有重要意义。

高阶偏导数的求解方法与普通函数的导数类似，只需要对一个自变量进行多次求导。

高阶导数与高阶偏导数

上一页下一页返回首页 2
三阶导数的导数称为四阶导数,
f(4)(x), y(4),
d4y .
dx4
一般地 ,函数 f(x)的 n1阶导数的导数称为
函数 f(x)的 n 阶导数 ,记作
f(n)(x), y(n), d dx ny n或 dn dfx(nx).
二阶和二阶以上的导数统称为高阶导数.
fy(x,y)x2x 3y2(x2 2x 3y y2 2)2,
湘潭大学数学与计算科学学院
上一页下一页返回首页 9
当 (x,y)(0,0)时 ,按定义可知：
fx(0 ,0 ) lx i0m f( x ,0 )x f(0 ,0 )lxi m00x 0,
fy(0,0) ly i0m f(0, y ) yf(0,0)
d2 y dxn

f (n) x.
湘潭大学数学与计算科学学院
上一页下一页返回首页 21
注 (1) d x n (d x )n ， d x n d (x n ) ， (dx)n表示微分的幂，简记为dxn；
d(xn)指幂的微分，即 d(xn)n xn 1dx ；而 d n x 是 x 的 n 阶微分 .
湘潭大学数学与计算科学学院
上一页下一页返回首页 6
观察上例中原函数、偏导函数与二阶混合偏导函数图象间的关系：
原函数图形
偏导函数图形
偏导
导二函阶
函
数混
数图
图合形偏
形
湘潭大学数学与计算科学学院
上一页下一页返回首页 7
例 3 设u eax cosby，求二阶偏导数.

高阶偏导数与全微分

y
( z ) y
2z y 2
zyy (x ，y)
f yy (x ，y)，
( z ) y x
2z xy
zxy (x ，y)
fxy (x ，y)，
( z ) x y
2z yx
zyx (x ，y)
f yx (x ，y)
其中，fxy (x ，y)，f yx (x ，y) 称为混合偏导数，它们是不
解因为圆柱体r2h
r 2 ，h 4 ，r h 0.01，
V dV 2π 2 4 0.01 π 22 0.01 0.628
所以，需用材料约为0.628立方米。
高等数学
例2 求函数 z x2 xy2 的全微分。
解 z 2x y2， x z 2xy y
两个偏导数都是连续的，所以全微分是存在的，即
dz (2x y2 )dx 2xydy
例3 求函数 z ex sin(x y) 的全微分。
解因为所以
z ex sin(x y) ex cos(x y)， x z ex cos(x y) y
高等数学
高阶偏导数与全微分
一、高阶偏导数
定义1 如果二元函数z=f(x, y)的偏导数 z ，z 仍然可导， x y
那么它们的偏导数称为函数z=f(x, y)的二阶偏导数．按照对自变量求导数次序不同，二元函数有下列四个二阶偏导数
( z ) x x
2z x2
zxx (x ，y)
fxx (x ，y)，
△z=A△x+B△y+o()．其中，A，B与△x，△y无关， (x)2 (y)2 ，o()是比高阶的无穷小，则称
A△x+B△y为函数z=f(x, y)在点(x, y)处的全微分，记作dz，即 dz Ax By

高阶偏导数

合集下载

第5节高阶偏导数

09-4_高阶偏导数

一偏导数定义及其计算法二高阶偏导数三小结

多元函数的偏导数与方向导数计算

第5节高阶偏导数资料讲解

第五节高阶偏导数

高阶偏导数

高阶导数与高阶偏导数

高阶偏导数及泰勒公式

高阶导数与高阶偏导数

7.5高阶偏导数与高阶全微分

高阶偏导数、方向导数与梯度PPT课件

高阶偏导数与高阶全微分

一偏导数的定义及其计算法二高阶偏导数三小结

高阶偏导数先代后求

高阶导数与高阶偏导数

高阶偏导数与全微分

文档推荐

最新文档