专题电磁感应中的导体棒

2025届高三物理一轮复习多维度导学与分层专练专题65电磁感应中的双棒问题导练目标导练内容目标1无外力等距式双棒问题目标2有外力等距式双棒问题目标3无外力不等距式双棒问题目标4有外力不等距式双棒问题【知识导学与典例导练】模型规律无外力等距式（导轨光滑）1、电流大小：21211212Blv Blv Bl(v v)IR R R R--==++2、稳定条件：两棒达到共同速度3、动量关系：2012()m v m m v=+4、能量关系：2122211m v(m m)v Q22=+共＋；1122Q RQ R=有外力等距式（导轨光滑）1、电流大小：1221Blv BlvIR R-=+2、力学关系：11AFam=；22AF Fam-=。

（任意时刻两棒加速度）3、稳定条件：当a2＝a1时，v2-v1恒定；I恒定；F A恒定；两棒匀加速。

4、稳定时的物理关系：12F (m m )a =+；1A F m a =；2112A Bl(v v )F BIlB lR R -==+；121212212(R R )m F v v B l (m m )+-=+无外力不等距式（导轨光滑）1、动量关系：11110BL I t m v m v -∆=-；2220BL I t m v -∆=-2、稳定条件：1122BL v BL v =3、最终速度：21222122110m L v v m L m L =+；12122122120m L L v v m L m L =+4、能量关系：222101122111222Q m v m v m v =--5、电量关系：2202BL q m v =-有外力不等距式（导轨光滑）F 为恒力，则：1、稳定条件：1122l a l a =，I 恒定，两棒做匀加速直线运动2、常用关系：111A F F a m -=；222A F a m =；1122l a l a =；1122A A F l F l =3、常用结果：2121221221A l m F F l m l m =+；1222221221A l l m F F l m l m =+；221221221l a F l m l m =+；122221221l l a F l m l m =+；此时回路中电流为：12221221l m F I l m l m B=⋅+与两棒电阻无关一、无外力等距式双棒问题【例1】如图，水平面内固定有两根平行的光滑长直金属导轨，导轨间距为l ，电阻不计。

2023届高三物理一轮复习重点热点难点专题特训专题67 电磁感应现象中的单棒问题特训目标 特训内容目标1 阻尼式单棒问题（1T —5T ） 目标2 电动式单棒问题（6T —10T ） 目标3发电式单棒问题（11T —15T ）一、阻尼式单棒问题1．如图所示，左端接有阻值为R 的定值电阻且足够长的平行光滑导轨CE 、DF 的间距为L ，导轨固定在水平面上，且处在磁感应强度为B 、竖直向下的匀强磁场中，一质量为m 、电阻为r 的导体棒ab 垂直导轨放置且静止，导轨的电阻不计。

某时刻给导体棒ab 一个水平向右的瞬时冲量I ，导体棒将向右运动，最后停下来，则此过程中（ ）A ．导体棒做匀减速直线运动直至停止运动B ．电阻R 上产生的焦耳热为22I mC ．通过导体棒ab 横截面的电荷量为I BLD ．导体棒ab 运动的位移为22IRB L 【答案】C【详解】A ．导体棒获得向右的瞬时初速度后切割磁感线，回路中出现感应电流，导体棒ab受到向左的安培力，向右减速运动，由22B L vma R r =+可知，由于导体棒速度减小，则加速度减小，所以导体棒做的是加速度越来越小的减速运动直至停止运动，A 错误；B ．导体棒减少的动能22211()222k I I E mv m m m ===根据能量守恒定律可得k E Q =总又根据串并联电路知识可得22()R R I R Q Q R r m R r ==++总，B 错误； C ．根据动量定理可得0BIL t mv -=-；I mv =；q I t =可得Iq BL=，C 正确； D ．由于E BLxq I t t R r R r R rΦ====+++将I q BL =代入可得，导体棒ab 运动的位移22()I R r x B L +=，D 错误。

故选C 。

2．如图所示，一根直导体棒质量为m 、长为L ，其两端放在位于水平面内、间距也为L 的光滑平行金属导轨上，并与之接触良好，导体棒左侧两导轨之间连接一可控电阻，导轨置于匀强磁场中，磁场的磁感应强度大小为B ，方向垂直于导轨所在平面。

电磁感应中的“杆+导轨”模型电磁感应中的“杆+导轨”模型一、单棒模型阻尼式：在单棒模型中，导体棒相当于电源，根据洛伦兹力的公式，可以得到安培力的特点为阻力，并随速度减小而减小，加速度随速度减小而减小，最终状态为静止。

根据能量关系、动量关系和瞬时加速度，可以得到公式B2l2v R rF和q mv/Bl，其中q表示流过导体棒的电荷量。

需要注意的是，当有摩擦或者磁场方向不沿竖直方向时，模型的变化会受到影响。

举例来说，如果在电阻不计的光滑平行金属导轨固定在水平面上，间距为L、导轨左端连接一阻值为R的电阻，整个导轨平面处于竖直向下的磁感应强度大小为B的匀强磁场中，一质量为m的导体棒垂直于导轨放置，a、b之间的导体棒阻值为2R，零时刻沿导轨方向给导体棒一个初速度v，一段时间后导体棒静止，则零时刻导体棒的加速度为0，零时刻导体棒ab两端的电压为BLv，全过程中流过电阻R的电荷量为mv/Bl，全过程中导体棒上产生的焦耳热为0.二、发电式在发电式中，导体棒同样相当于电源，当速度为v时，电动势E＝Blv。

根据安培力的特点，可以得到公式22Blv/l＝Blv/(R＋r)。

加速度随速度增大而减小，最终特征为匀速运动。

在稳定后的能量转化规律中，F-BIl-μmg=m*a，根据公式可以得到a=-(F-μmg)/m、v=0时，有最大加速度，a=0时，有最大速度。

需要注意的是，当电路中产生的焦耳热为mgh时，电阻R中产生的焦耳热也为mgh。

1.如图所示，相距为L的两条足够长的光滑平行金属导轨MN、PQ与水平面的夹角为θ，N、Q两点间接有阻值为R的电阻。

整个装置处于磁感应强度为B的匀强磁场中，磁场方向垂直导轨平面向下。

将质量为m、阻值也为R的金属杆cd垂直放在导轨上，杆cd由静止释放，下滑距离x时达到最大速度。

重力加速度为g，导轨电阻不计，杆与导轨接触良好。

求：1)杆cd下滑的最大加速度和最大速度；2)上述过程中，杆上产生的热量。

导体切割磁感线问题电磁感应中，“导体棒”切割磁感线问题是高考常见命题。

解此类型问题的一般思路是：先解决电学问题，再解决力学问题，即先由法拉第电磁感应定律求感应电动势，然后根据欧姆定律求感应电流，求出安培力，再往后就是按力学问题的处理方法，如进行受力情况分析、运动情况分析及功能关系分析等。

（如果学生能力足够，完全可以力学和电学同时分析，找到中间那个联系点，一般联系点都是合力，之后运用牛二定律很容易解题。

）导体棒切割磁感线的运动一般有以下几种情况：匀速运动、在恒力作用下的运动、恒功率运动等。

一、导体棒匀速运动导体棒匀速切割磁感线处于平衡状态，安培力和外力等大、反向，给出速度可以求外力的大小，或者给出外力求出速度，也可以求出功、功率、电流强度等，外力的功率和电功率相等。

例1. 如图1所示，在一磁感应强度B＝0.5T的匀强磁场中，垂直于磁场方向水平放置着两根相距为h＝0.1m的平行金属导轨MN和PQ，导轨电阻忽略不计，在两根导轨的端点N、Q 之间连接一阻值R＝0.3Ω的电阻。

导轨上跨放着一根长为L＝0.2m，每米长电阻r＝2.0Ω/m的金属棒ab，金属棒与导轨正交放置，交点为c、d，当金属棒在水平拉力作用于以速度v＝4.0m/s向左做匀速运动时，试求：图1（1）电阻R中的电流强度大小和方向；（2）使金属棒做匀速运动的拉力；（3）金属棒ab两端点间的电势差；（4）回路中的发热功率。

解析：金属棒向左匀速运动时，等效电路如图2所示。

在闭合回路中，金属棒cd部分相当于电源，内阻r cd＝hr，电动势E cd＝Bhv。

图2（1）根据欧姆定律，R中的电流强度为0.4A，方向从N经R到Q。

（2）使金属棒匀速运动的外力与安培力是一对平衡力，方向向左，大小为F＝F安＝BIh＝0.02N。

（3）金属棒ab两端的电势差等于U ac、U cd与U db三者之和，由于U cd＝E cd－Ir cd，所以U ab ＝E ab－Ir cd＝BLv－Ir cd＝0.32V。

电磁感应中的导体棒问题电磁感应中的导轨上的导体棒问题是历年高考的考点。

该类问题是力学和电学的综合问题，通过它可以考查考生综合运用知识的能力。

解滑轨上导体棒的运动问题，首先要挖掘出导体棒的稳定条件及它最后能达到的稳定状态，然后才能利用相关知识和稳定条件列方程求解。

一、滑轨上只有一根导体棒的问题滑轨上只有一个导体棒的问题，分三类情况：一种是含电源闭合电路的导体棒问题，另一种是闭合电路中的导体棒在安培力之外的力作用下的问题。

第三种是含有电容器的问题。

（一）含电源闭合电路的导体棒问题例1 如图1所示，水平放置的光滑导轨MN 、PQ 上放有长为L 、电阻为R 、质量为m 的金属棒ab ，导轨左端接有内阻不计、电动势为E 的电源组成回路，整个装置放在竖直向上的匀强磁场B 中，导轨电阻不计且足够长，并与电键S 串联。

当闭合电键后，求金属棒可达到的最大速度。

（二）闭合电路中的导体棒在安培力之外的力作用下的问题 1. 导体棒在外力作用下从静止运动问题例2 如图所示，倾角θ=30º、宽度L =1m 的足够长的“U ”形平行光滑金属导轨固定在磁感应强度B =1T ，范围充分大的匀强磁场中，磁场方向垂直于斜面向下。

用平行于轨道的牵引力拉一根质量m =0.2㎏、电阻R =1Ω放在导轨上的金属棒a b ，使之由静止沿轨道向上移动，牵引力做功的功率恒为6W ，当金属棒移动2.8m 时，获得稳定速度，在此过程中金属棒产生的热量为5.8J ，不计导轨电阻及一切摩擦，取g =10m/s 2。

求：（1）金属棒达到稳定时速度是多大？（2）金属棒从静止达到稳定速度时所需的时间多长？2. 外力作用下有初速问题例3 如图4所示，匀强磁场竖直向上穿过水平放置的金属框架，框架宽为L ，右端接有电阻为R ，磁感应强度为B ，一根质量为m 、电阻不计的金属棒受到外力冲量后，以的初速度沿框架向左运动，棒与框架的动摩擦因数为，测得棒在整个运动过程中，通过任一截面的电量为q ，求：（1）棒能运动的距离？（2）R 上产生的热量？ （三）含有电容器的问题例4 【2013新课标 25】(19分)如图．两条平行导轨所在平面与水平地面的夹角为θ，间距为L 。

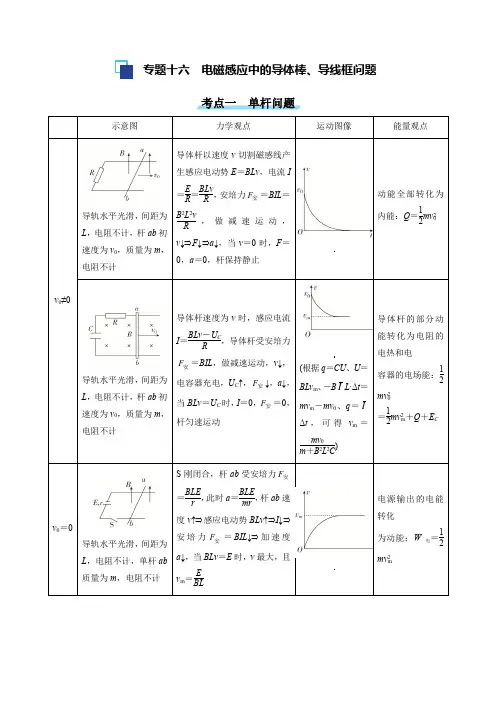
专题十六电磁感应中的导体棒、导线框问题考点一单杆问题导轨水平光滑，间距为L，电阻不计，杆ab初速度为v0，质量为m，电阻不计导轨水平光滑，间距为L，电阻不计，杆ab初速度为v0，质量为m，电阻不计，，(根据q＝CU、U＝BLv m、－B I L·Δt＝mv m－mv0、q＝IΔt，可得v m＝mv0m＋B2L2C)导轨水平光滑，间距为L，电阻不计，单杆ab 质量为m，电阻不计导轨水平光滑，间距为L，电阻不计，单杆ab质量为m，电阻不计，拉力F恒定最大，导轨水平光滑，间距为L，电阻不计，单杆ab 质量为m，电阻为R (根据Δq＝q0－q ＝CE－CBLv m、B I LL·Δt＝mv m－0、Δq＝IΔt，可得v m＝BLCEm＋B2L2C)导轨水平光滑，间距为L，电阻不计，单杆ab 质量为m，电阻不计，拉力F恒定(2022·山东省菏泽市高三下二模)如图所示，倾角为θ的斜面上固定两根足够长的平行光滑导轨，将定值电阻、电容器和电源在导轨上端分别通过开关S 1、S 2、S 3与导轨连接，匀强磁场垂直斜面向下，初始时刻导体棒垂直导轨静止，不计导轨和导体棒的电阻，下列叙述正确的是( ) A .S 1闭合，S 2、S 3断开，由静止释放导体棒，导体棒的a ­t 图像如图1 B .S 2闭合，S 1、S 3断开，由静止释放导体棒，导体棒的a ­t 图像如图2C .S 1、S 2、S 3断开，由静止释放导体棒Δt 后闭合开关S 1，导体棒的v ­t 图像可能如图3D .S 1、S 2、S 3断开，由静止释放导体棒Δt 后闭合开关S 3，导体棒的v ­t 图像一定如图4CS 1闭合，S 2、S 3断开，由静止释放导体棒，导体棒与电阻构成回路，根据E ＝BLv ，I ＝ER ，F 安＝BIL ，可得F 安＝B 2L 2v R ，根据牛顿第二定律可得导体棒的加速度为a ＝mg sin θ－F 安m ＝g sin θ－B 2L 2vmR ，可知随着导体棒速度的增加，导体棒的加速度逐渐减小，A 错误；S 2闭合，S 1、S 3断开，由静止释放导体棒，导体棒与电容器构成回路，则有E ＝BLv ，电容器极板所带电荷量为Q ＝CE ＝CBLv ，电路中电流为I ＝ΔQ Δt ＝CBL ΔvΔt ＝CBLa ，导体棒受到的安培力为F 安＝BIL ＝CB 2L 2a ，根据牛顿第二定律可得mg sin θ－F 安＝ma ，解得a ＝mg sin θm ＋CB 2L 2，可知导体棒的加速度保持不变，B 错误；S 1、S 2、S 3断开，由静止释放导体棒Δt 后闭合开关S 1，可知闭合开关S 1瞬间导体棒的速度为v ＝g sin θ·Δt ，导体棒受到的安培力大小为F 安＝B 2L 2v R ＝B 2L 2g sin θ·ΔtR ，若F 安＝B 2L 2g sin θ·ΔtR <mg sin θ，可知导体棒继续向下加速，随着速度的增加，安培力增大，加速度减小，当安培力与重力沿导轨向下的分力平衡时，导体棒做匀速直线运动，故导体棒的v ­t 图像可能如图3，C 正确；S 1、S 2、S 3断开，由静止释放导体棒Δt 后闭合开关S 3，可知闭合开关S 3瞬间导体棒的速度为v ＝g sin θ·Δt ，导体棒切割磁感线产生的电动势为E 动＝BLv ＝BLg sin θ·Δt ，根据右手定则可知动生电动势E 动的方向与电源的电动势E 0方向相反，若E 动＝BLg sin θ·Δt >E 0，则回路的电流为I ＝E 动－E 0r ＝BLg sin θ·Δt －E 0r ，安培力方向沿导轨向上，大小为F 安＝BIL ＝BL ·BLg sin θ·Δt －E 0r ，若刚好满足F 安＝BL ·BLg sin θ·Δt －E 0r ＝mg sin θ，则导体棒向下做匀速直线运动，D 错误。

2024版新课标高中物理模型与方法电磁感应中的双导体棒和线框模型目录一.无外力等距双导体棒模型二．有外力等距双导体棒模型三．不等距导轨双导体棒模型四．线框模型一.无外力等距双导体棒模型【模型如图】1.电路特点棒2相当于电源；棒1受安培力而加速起动,运动后产生反电动势.2.电流特点：I =Blv 2−BLv 1R 1+R 2=Bl (v 2−v 1)R 1+R 2随着棒2的减速、棒1的加速，两棒的相对速度v 2−v 1变小，回路中电流也变小。

v 1=0时：电流最大，I =Blv 0R 1+R 2。

v 1=v 2时：电流　I =03.两棒的运动情况安培力大小：F 安=BIl =B 2L 2(v 2−v 1)R 1+R 2两棒的相对速度变小,感应电流变小,安培力变小.棒1做加速度变小的加速运动，棒2做加速度变小的减速运动，最终两棒具有共同速度。

4.两个规律(1)动量规律：两棒受到安培力大小相等方向相反,系统合外力为零,系统动量守恒.m 2v 0=(m 1+m 2)v 共(2)能量转化规律：系统机械能的减小量等于内能的增加量.(类似于完全非弹性碰撞)Q =12m 2v 20−12(m 1+m 2)v 2共两棒产生焦耳热之比：Q 1Q 2=R 1R 2；Q =Q 1+Q 25.几种变化：(1)初速度的提供方式不同(2)磁场方向与导轨不垂直(3)两棒都有初速度(两棒动量守恒吗？)(4)两棒位于不同磁场中(两棒动量守恒吗？)1(2023春·江西赣州·高三兴国平川中学校联考阶段练习)如图所示，MN 、PQ 是相距为0.5m 的两平行光滑金属轨道，倾斜轨道MC 、PD 分别与足够长的水平直轨道CN 、DQ 平滑相接。

水平轨道CN 、DQ 处于方向竖直向下、磁感应强度大小为B =1T 的匀强磁场中。

质量m =0.1kg 、电阻R =1Ω、长度L =0.5m 的导体棒a 静置在水平轨道上，与a 完全相同的导体棒b 从距水平轨道高度h =0.2m 的倾斜轨道上由静止释放，最后恰好不与a 相撞，运动过程中导体棒a 、b 始终与导轨垂直且接触良好，导轨电阻不计，重力加速度g 取10m/s 2。

电磁感应中的导轨上的导体棒问题，是力学和电学的综合问题。

解决 电磁感应中的导轨上的导体棒问题 ，首先要挖掘出导体棒的稳定条件及它最后能达到的稳定状态，然后才能利用相关知识和稳定条件列方程求解。

下文是常见导轨上的导体棒问题的分类及结合典型例题的剖析。

想必你阅过全文，你会对滑轨上的导体棒运动问题，有一个全面的细致的了解，能迅速分析出稳定状态，挖掘出稳定条件，能准确的判断求解所运用的方法。

一、滑轨上只有一个导体棒的问题滑轨上只有一个导体棒的问题，分两类情况：一种是含电源闭合电路的导体棒问题，另一种是闭合电路中的导体棒在安培力之外的力作用下的问题。

（一）含电源闭合电路的导体棒问题例 1、如图1所示，水平放置的光滑导轨MN、PQ上放有长为L、电阻为R、质量为m的金属棒 ab ，导轨左端接有内阻不计、电动势为E的电源组成回路，整个装置放在竖直向上的匀强磁场B中，导轨电阻不计且足够长，并与电键S串联。

当闭合电键后，求金属棒可达到的最大速度。

图 1分析：本题的稳定状态是金属棒最后的匀速运动；稳定条件是金属棒的加速度为零（安培力为零，棒产生的感应电动势与电源电动势大小相等）。

解析：闭合电键后，金属棒在安培力的作用下向右运动。

当金属棒的速度为v时，产生的感应电动势，它与电源电动势为反接，从而导致电路中电流减小，安培力减小，金属棒的加速度减小，即金属棒做的是一个加速度越来越小的加速运动。

但当加速度为零时，导体棒的速度达到最大值，金属棒产生的电动势与电源电动势大小相等，回路中电流为零，此后导体棒将以这个最大的速度做匀速运动。

金属板速度最大时，有解得（二）闭合电路中的导体棒在安培力之外的力作用下的问题1.导体棒在外力作用下从静止运动问题例 2、 如图 2，光滑导体棒 bc固定在竖直放置的足够长的平行金属导轨上，构成框架 abcd ，其中 bc棒电阻为R，其余电阻不计。

一质量为m且不计电阻的导体棒 ef 水平放置在框架上，且始终保持良好接触，能无摩擦地滑动。