当前位置：文档之家 › 动量算符及角动量算符的球坐标表示.pdf

动量算符及角动量算符的球坐标表示.pdf

  • 格式：pdf
  • 大小：3.17 MB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

角动量算符

角动量算符



pˆ z z

i
写成通式:
但是坐标算符与其非共轭动量 对易，各动量之间相互对易。
x pˆ pˆ x i
pˆ pˆ pˆ pˆ 0
, x, y, z
量子力学中最基本的 对易关系。
xpˆ y pˆ y x 0

xpˆ z

pˆ z
( Aˆ Bˆ ) Bˆ Aˆ 13
(11)厄密共轭算符
算符 Ô 之厄密共轭算符 Ô+ 定义:
由此可得：:
d *Oˆ d (Oˆ )*
d *Oˆ d (Oˆ )*
转置算符 的定义
厄密共轭 算符亦可 写成：
[ d *(Oˆ )]*
讲解人：沈建其
第四章 量子力学中的力学量
本块内容广博，务必以自学为主。 自我教育，修炼成材，系大学教育目标之一。
– §1 算符的运算规则 §2 动量算符和角动量算符 （§1 与§2可就所发曾谨言教程复印材料第三章学习）
§3 电子在库仑场中的运动 §4 氢原子 （用薛定谔方程再探氢原子，与Bohr半经典半量子理论思路不同） (§3和§4对照本ppt学习，学习其数学思路)
x

(i
x
)x

i

ix
x

xpˆ x pˆ x x
而
（xpˆ x pˆ x x） i
因为 是任意波函数，
所 以 xpˆ x pˆ x x i
对8 易
关系
同理可证其它坐标算符
与共轭动量满足
ypˆ y pˆ y y i

zpˆ z
n0
设给定一函数 F(x), 其各阶导数均存在, 其幂级数展开收敛
量子力学——算符（精品pdf）

量子力学——算符（精品pdf）

量子力学
算符
目录
一、位置算符
1.1 厄米算符 1.2 （位置算符）本征值与本征函数
1.3 正则对易关系
二、动量算符
2.1 动量算符导引 2.2 （动量算符）本征值与本征函数
七、自旋算符
7.1 概论 7.2 发展史 7.3 自旋量子数
7.3.1 基本粒子的自旋 7.3.2 亚原子粒子的自旋 7.3.3 原子和分子的自旋
中心的角色。角动量，动量，与能量是物体运动的三个基
本特性
目录 3.1 简介 3.2 数学定义 3.3 角动量是厄米算符 3.4 对易关系
3.4.1 角动量算符算符与自己的对易关系 3.4.2 角动量平方算符与角动量算符之间的对易关系 3.4.3 哈密顿算符与角动量算符之间的对易关系 3.4.4 在经典力学里的对易关系 3.5 (角动量)本征值与本征函数
目录 1.1 厄米算符 1.2 本征值与本征函数 1.3 正则对易关系
返回目录 3/52
1.1厄米算符
由于每一种经过测量而得到的物理量都是实值的。所以，可观察量 O 的期望值是 实值的：
对于任意量子态 ，这关系都成立：
根据伴随算符的定义，假设 是 的伴随算符，则
因此，
这正是厄米算符的定义。所以，表示可观察量的算符 ，都是厄米算符。
2.3 厄米算符 2.4 正则对易关系
7.3.4 自旋与统计
7.4 自旋的方向
三、角动量算符
3.1 简介 3.2 数学定义 3.3 角动量是厄米算符 3.4 对易关系
3.4.1 角动量算符算符与自己的对易关系 3.4.2 角动量平方算符与角动量算符之间的对易关系 3.4.3 哈密顿算符与角动量算符之间的对易关系
经过一番繁杂的运算，终于得到想要的方程
动量算符和角动量算符

动量算符和角动量算符


周期性边界条件
在箱子边界的对应点A, A’上加上其波函数相等的条件，此边 界条件称为周期性边界条件。
y
rA
L 2
,
y,
z
A’ o
rA
L 2
,
y,
z
A
x
ce i [
px
L 2
p
y
y
pz
z
]
ce i
[
px
L 2
p
y
y
pz
z
]
z
L
由此得：
ei
pxL
1
于是有：
1
px L
2nx
px
2nx
§3.2 动量算符和角动量算符
1.动量算符 2.角动量算符
1.动量算符
（1）动量算符 （2）动量本征方程 （3）求解动量本征方程 （4）归一化系数的确定 （5）箱归一化
（1）动量算符
pˆ i
pˆ x
i
d dx
pˆ y
i
d dy
pˆ z
i
d dz
（2）动量本征方程
i
p
(r )
p
p
(r )
Ylm ( , ) (1)m Yl*m ( , )
m 1,2,3,,l
m的取值受的限制。对应一个 值，m 取值为 0, ±1, ±2, ±3, ..., ± 共 (2 +1)个值。即当 确定后，尚有(2 +1)个磁量 子状态不确定。换言之，对应一个值有(2 +1)个量子状态，这 种现象称为简并， 的简并度是 (2 +1) 度。
对于任意函数f (r, θ, φ)（其中，r, θ, φ都是 x, y, z 的函数）有
力学量的算符表示和平均值

力学量的算符表示和平均值

§15-3 力学量的算符表示和平均值
一、力学量的算符表示 量子力学中描述系统的每一个力学量对应一个算符。 与动量相对应的算符 动量分量的算符
p x i x p y i y p z i z
ˆ p i
与动量平方相对应的算符是
ˆ 2 2 2 p
与能量相对应的算符
2 2 ˆ H U (r ) 2
称为哈密顿算符
1
角动量算符为
直角坐标系中的分量式
ˆrp ˆ L
球坐标系中的分量式
ˆ Lx i(sin cot cos ) ˆ i( cos cot sin ) Ly ˆ i Lz
2
2
角动量平方算符也可以表示为
2 1 ˆ2 ˆ2 L (sin ) 2 Lz sin sin
二、本征函数、本征值和平均值
算符是代表对波函数的一种运算，是把一个波函数 或量子态变换成另一个波函数或量子态。 A A
此式为力学量的本征值方程，常量A称为力学量的本征值。
角动量平方算符为
ˆ ˆ ˆ ˆ L2 L2 L2y L2 x z
1 1 ˆ ˆ L2 2 [ (sin ) 2 ] 2 Ω 2 sin sin
式中算符
1 1 (sin ) sin sin 2
ˆ yp zp i( y z ) ˆz ˆy Lx z y ˆ zp xp i( z x ) ˆx ˆz Ly x z ˆ xp yp i( x y ) ˆy ˆx Lz y x
引入哈密顿算符后，定态薛定谔方程可以简化为 ˆ
3.2 动量算符和角动量算符

3.2 动量算符和角动量算符

动量算符的本征方程
本征方程
力学量算符
本征值波函数 本征值
本征值和本征波函数由本征值方程得到 动量算符
动量算符的本征态
解以上方程得
c为归一化常数
归一化出现问题,发散 px = px’ 两种归一方法
利用
( x)
x
这样一来
同时我们从解本征方程看，动量的本征值可取任意值， 连续谱，在处理动量问题时，常把动量的连续本征值变 为分立值，最后在把分立体征值实回到连续本征值。
箱中粒子波函数是动量取分立值的平面波
角动量算符
角动量平方算符
角动量平方算符
角动量算符——球坐标系中的表示
球坐标中P点，直角坐标表示（x,y,z) 球坐标（ r, , ），
z
p
r

y
ห้องสมุดไป่ตู้
在球坐标下，以上算符
有怎样的具体形式？
x
角动量算符——球坐标系中的表示
例如
由
角动量算符——球坐标系中的表示
定轴转动呢？
本征方程
方程求解是困难的 物理要求在整个区域有限
在直坐标 球坐标
角动量算符的本征值和本征函数
有限条件 解是球函数
勒让德多项式
角动量算符的本征函数的归一化
球谐函数
角动量算符的本征值和本征函数
L为角量子数
m为磁量子数
量子数？
角动量算符的本征值问题的应用
应用转动问题 刚性转子 定态薛方程 刚体运动分解 为平动和转动
角动量算符——球坐标系中的表示
这样就求得了 同样方法可求得 带入
角动量算符——球坐标系中的表示
(1)
(2)
(3)
角动量算符——球坐标系中的表示
动量算符角动量算符

动量算符角动量算符


这时，方程(19)的解是球谐函数 Ylm ( ,) ： Ylm(,) NlmPl m (cos)eim m 0, 1, 2, l (21) Pl m (cos ) 是缔合勒让德多项式，Nlm 是归一化常数。
Nlm由Ylm ( ,) 的归一化条件定出：
0
2 0
Ylm ( ,)Ylm ( ,) sin d d
2 1
sin
(sin
)
1 sin2
2
2
(18)
３、角动量 z 分量算符 Lˆz ：
Lˆz i
(16)
Lˆ2z
2 2
2
４、角动量平方算符的本征值方程：
2
1
sin
(sin
)
1
sin2
2
2
Y
(
,)
2Y ( ,) (18)
或 sin1
(sin
)
1 sin2
§3.2 动量算符和角动量 算符
一、动量算符
１、动量算符的本征值方程
i p (r ) p p (r ) (1)
函p 是数。动分量量算式符：的本征i 值，xpp((rr))是属px于 p此(r本) 征值的本征
i
y
p (r )
py
p (r )
i
z
p (r )
pz
p (r )
它们的解是 p (r ) C exp( i p r ) (2)
二、角动量算符
１、定义：角动量算符 L rˆ pˆ (12)
分量式为
Lˆx ypˆ z zpˆ y
( y z ) i i z y
(y z ) z y
Lˆy zpˆ x xpˆ z
(z x ) i i x z
动量算符和角动量算符

动量算符和角动量算符

显然有如下性质
lˆ++ = lˆ− ， lˆ−+ = lˆ+
这两个算符不是厄密算符。 (II) 对易关系
[lˆz , lˆ± ] = ±hlˆ± ， [lvˆ 2 , lˆ± ] = 0 ， lˆ+lˆ− = lvˆ 2 − lˆz2 + hlˆz ， lˆ−lˆ+ = lvˆ 2 − lˆz2 − hlˆz ④ Lˆ2 在球坐标中的表示
exp⎢⎣⎡
i h
( px
−
px′ )⎥⎦⎤dx
=
2πhδ
( px
−
px′ )
∫∞ −∞
exp⎢⎣⎡
i h
(py
−
p y′ )⎥⎦⎤dy
=
2πhδ
(
py
−
py′ )
∫∞ −∞
exp⎢⎣⎡
i h
( pz
−
pz′ )⎥⎦⎤dz
=
2πhδ ( pz
−
pz′ )
式中 δ ( px − p′x ) 是以 px − p′x 为宗量的 δ 函数，故有
§3.2 动量算符和角动量算符 1．动量算符和本征方程 1). 动量算符
当波函数ψ 表示为坐标 x 、y 、z 的函数时，动量 p 和动量算符 − ih∇ 相对应，定义动量算符 pˆ ：
pr → prˆ = −ih∇
px
=
−ih
∂ ∂x
py
=
−ih
∂ ∂y
pz
=
−ih
∂ ∂z
本征方程： 各分量方程：
∂ ∂x
−
x
∂ )
∂z
lˆz
=
xpˆ y
−
3.2 动量和角动量算符

3.2 动量和角动量算符

0
得归一化的波函数为
1 imϕ Φm (ϕ) = e 2π
(m = 0, ±1, ±2,⋯ )
L2的本征值问题
ˆ L2Y (θ , ϕ ) = λ ℏ 2Y (θ , ϕ )
L2 的本征值方程可写为：
1 ∂ ∂ 1 ∂2 −ℏ [ (sin θ )+ 2 ]Y (θ , ϕ ) = λ ℏ 2Y (θ , ϕ ) (3.2.16) sin θ ∂θ ∂θ sin θ ∂φ 2 或：
的本征方程 L2的本征方程
ˆ L2Ylm (θ , ϕ ) = l (l + 1)ℏ 2Ylm (θ , ϕ )
(3.2.22） ） Lz的本征方程
ˆ LzYlm (θ , ϕ ) = mℏYlm (θ , ϕ )
(3.2.23） ）
→
l z = mℏ
m = 0,±1,±2, ⋯
例: 若体系的波函数就是球谐函数 Y20 (θ , ϕ ) (1)求其角动量矢量与 z 轴的加角. 求其角动量矢量与 轴的加角
2
1 ∂ ∂ 1 ∂2 [ (sin θ )+ 2 ]Y (θ , ϕ ) = −λY (θ , ϕ ) 2 sin θ ∂θ ∂θ sin θ ∂φ
(3.2.17)
其中 Y(θ,ϕ) 是 L2 属于本征值 Y(θ λℏ2 的本征函数。此方程就是球谐函数方程 ℏ 的本征函数。 为使 Y(θ,ϕ) 在θ 变化的区域(0, π)内是有限的， 则必须满足：λ = ℓ（ℓ + 1), 其中 ℓ = 0, 1, 2, ... (3.2.18） ）
− iℏ∇ψ p (r ) = pψ p (r )
求解 采用分离变量法，令： 采用分离变量法，
（3.2.1） ）
ψ p ( r ) = ψ ( x )ψ ( y )ψ ( z )
动量算符及角动量算符的球坐标表示

动量算符及角动量算符的球坐标表示

=p •
一
很显然动量算符的 r,0 分量 仇 形式为
九 ＝－访
a
1
a
O
8r
r 汾
分量
r
r
^ ，过渡到量子力学，由于 p 和 r 不对易，为了保证径向
l
8
rsin 0 8<p
。
动量算符是厄密算符我们可以取
仇＝早 • 6 + 6 • _i:_) = -itz立 ＿ 竺 2 r r ar r
这才是动量径向分量的算符表示，它满足厄密性的要求。 同理，可以构造 九＝—他 • p +p • e。) = - in.- — - in. 。它 2 r 80 2rt的 也满足厄密性的要求。 2.2.3 -in
在世子力学中，动匮打符P= ih'v这样角动扭环符表示为 l-= ;- f, =-盼X'v
代入(1), 表示成直角坐标系中的(i j k)方向
这样就得到了CL. 工，L.)的球坐标表示式 L, a a := iii(sin!p -十ctgfJcos!p一） afJ 呼
四、推出球坐标中C'的表示式 由(5)可知 一 - a8· aO· -=r·= cos旰· ＇ 、J 动 砰
r 汾
= -itz — - — ，
6
巾
Or
r
I 8
1
2rtg0
， p~ = - iii
1
a
rsin 0 acp
。
' . ' ^ =-ism <p + jcos<p 由坐标变换得 e
- in
1
rsin 0
— = e0 • p
匈
8
•
,
= ~ism <p + j cos<p X九 - y y
3.2动量算符和角动量算符

3.2动量算符和角动量算符

§3.2 动量算符和角动量算符一．动量算符。

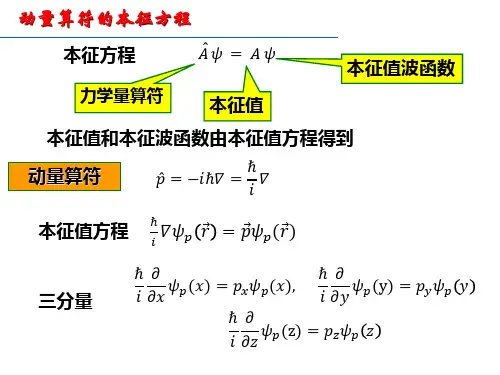
1. 动量算符的本征值方程：()()r p r ip p ψψ=∇，三个分量方程是 （3.2.1） ()()r p r xi p x p ψψ=∂∂ ， +∞<<∞-x ()()r p r yi p y p ψψ=∂∂ ， +∞<<∞-y （3.2.2） ()()r p r zi p z p ψψ=∂∂ ， +∞<<∞-z 通解是()r p i pCe r∙=ψ，C 是归一化常数。

（3.2.3） 2.动量本征函数的归一化。

()()()()()[]⎰⎰⎰⎰∞+∞-∞+∞-∞+∞-'-+'-+'-∙∞+∞-=dxdydze C d r r z p p y p p x p p ip pz z y y x x2τψψ因为()()x x x p p ip p dx ex x '-=⎰∞+∞-'-δπ2，所以有()()()()()()()()p p C p p p p p p C d r r z z y y x x p p'-='-'-'-=∙+∞∞-⎰δπδδδπτψψ323222如果取()232-= πC ，则()r pψ归一化为δ函数。

()()()()()r p i pp per p p d r r∙∙+∞∞-='-=⎰2321;πψδτψψ（3.2.4）（3.2.5）3.箱归一化在A （L/2,y,z ）和A '(-L/2,y,z)点, ()r p i p Ce r∙=ψ的值应相同。

即⎪⎭⎫⎝⎛++⎪⎭⎫⎝⎛++-=z p y p L p i z p y p L p i z y x z y x CeCe2121()1=L p ix e所以πx xn L p 2=，x n 是正负整数或零。

,1,0,2±==x xx n Ln p π （3.2.6）,1,0,2±==y yy n Ln p π （3.2.7）,1,0,2±==z zz n Ln p π （3.2.8） 当L ∞→时，z y x p p p ,,的本征值就变为连续谱。

动量算符角动量算符

动量算符角动量算符


i ( r ) p ( r ) ( 1 ) p p
函数。
p 是动量算符的本征值， p ( r ) 是属于此本征值的本征

分量式：
i p ( r ) p x p ( r ) x i p ( r ) p y p ( r ) y i p ( r ) p z p ( r ) z
它们的解是
i ( r ) C e x p (p r ) ( 2 ) p
本征值 ( 可取所有实数，构成连续谱。 ppp ,y ,z ) p x
２、动量本征函数的归一化
i 求归一化常数 C ？ ( r ) C e x p ( pr ) p
() r () r d 计算积分： p p 2
可得
ˆ Lx i (sin ctg cos ) ˆ Ly i (cos ctg sin ) (16) ˆ Lz i x

y

和
2 2 2 ˆ L ( 1 7 ) z 2

N Pl (cos ) 是缔合勒让德多项式，
m
lm
是归一化常数。
N
lm
由 Ylm ( , ) 的归一化条件定出：
Y ( , ) Y ( , )s in d d 1 ( 2 2 ) l m l m

2
0 0
( lm ) !2 l 1 得 N ( 2 3 ) l m ( lm ) !4
即 r ) ( rd ) ( p p ) ( 3 ) ( p p
( r ) p 其中 3 ( 2 )2 为什么 p ( r ) 不能归一化为1，而是归一化为 函数： 这是由于动量本征值可以取连续值， p 的各分量可取任 意实数，动量本征值构成连续谱。

3.2动量算符和角动量算符


i
2
exp[ ( px p x ) x ]dx exp[ ( p y p y ) y ]dy exp[ ( p z p z )z ]dz

i

i
2 3 C 2 (2 )3 ( px p ) ( p p ) ( p p ) C (2 ) ( p p) ( p p) x y y z z
一、 动量算符 (Momentum operator)
ˆ i p
x p i ( , x, y, z )
ˆx p ˆxx i xp ˆ x i p ˆy p ˆyy i yp x ˆ ˆzz i zp z p ˆ y i p ˆy p ˆyx 0 y xp ˆz p ˆz y 0 yp ˆ z i zp p ˆxz 0 z ˆ x p
§3.2 动量算符和角动量算符
p (r ) 本征值方程: i p (r ) p
i x p px p p p y p 三个分量方程: i y p pz p i z
解之得:
p (r ) Ce
i
pr
第三章 量子力学中的力学量
3/34
Quantum mechanics
§3.2 动量算符和角动量算符
归一化常数的确定:


* p (r )dxdydz p ( r )
2
C C




exp[ ( px p x ) x ( p y p y ) y ( p z p z ) x ]dxdydz i
ˆ x F Fp ˆ x i p ˆ y F Fp ˆ y i p ˆ z F Fp ˆ z i p F x F y F z

第三章-力学量的算符表示

px能够取-~+中连续变化旳一切实数，为了拟定C，考虑积分
p
'
x
(
x)
px (x)dx
CC
exp(i
px
px
x)dx
因为
1
exp(ikx)dx (k)
2
13
p'x
( x)
px
( x)dx
C
2
2 ( px
p'x
)
假如取 C
1
2
,
px (x) 的归一化为 函数
p'x
( x)
简并：一种本征值相应一种以上本征函数旳情况
简并度：相应于同一本征值旳本征函数旳数目
27
LˆzYlm mYlm
在Ylm态中，体系角动量在z方向上旳投影为m 前面几种球函数
1
Y00 4
Y1,1
3 sinei 8
Y1,0
3 cos 4
Y1,1
3 sinei 8
28
3.5 厄密算符本征函数旳性质
31
f重简并： 对一种本征值ln, 若同步有f个本征函数与之相应
属于同一种本征值ln旳简并波函数ψnk,，有
Lˆ nk ln nk , k 1, ..., f
一般来说，ψnk不正交， 但总能够找到正交函数。
例题 对下面两个氢原子旳未归一化旳1s和2s电子旳波函数
1s (r, , ) 1s (r) er /a ,
假如 Aˆ Bˆ BˆAˆ 0 则Aˆ 和Bˆ对易 记为 [ Aˆ, Bˆ] Aˆ Bˆ BˆAˆ 0
例 [xˆ, pˆ x ] ?
(xˆpˆ x
pˆ x xˆ)
ix

动量算符和角动量算符


Lˆ+
=
Lˆx
+ iLˆy
=
ih(−ieiϕ
∂ ∂θ
+ ctgθeiϕ
∂) ∂ϕ
( )( ) ( ) Lˆ+ Lˆ− = Lˆx + iLˆ y Lˆx − iLˆ y = Lˆ2x + Lˆ2y − i Lˆx Lˆ y − Lˆ y Lˆx = Lˆ2 − Lˆ2Z − i(ihLˆz )
所以
见p88 [Lˆx , Lˆ y ] = ihLˆz
[lˆα , pˆ β ] = ihεαβγ pˆγ
——注意到笛卡尔尔坐标 x 、 y 、 z 和球极坐标 r、θ、ϕ 之间的关系：
x = r sinθ cosϕ ， y = r sinθ sinϕ ，z = r cosθ
4
r 2 = x2 + y 2 + z 2 ， cosθ = z ， tgϕ = y
其中α , β = x, y, z 或1, 2,3
证明：
[xα , lˆβ ] = ihεαβγ xγ
或
[lˆα , xβ ] = ihεαβγ xγ
α, β = x, y, z
[ pˆα , lˆβ ] = ihεαβγ pˆγ 或 [lˆα , lvˆ 2 ] = 0
②在球坐标系中角动量算符的对易关系
=
c exp⎢⎣⎡hi
(1 2
pxl
+
py
y
+
pz z)⎥⎦⎤
或
exp⎜⎛ ⎝
i h
p
x
l
⎟⎞ ⎠
=1
因
exp⎜⎛ ⎝
i h
p
x
l
⎟⎞ ⎠

球坐标角动量算符

球坐标角动量算符
1、球坐标角动量算符
球坐标角动量是描述机构运动活动中的三维运动情况的一种特
殊算符。

它本质上是由一系列三元欧拉角的偏导数构成，它可以用来表示运动活动中机构的转速、旋转角速度和加速度。

以下是球坐标角动量算符：
（i）L = Jθ,其中L是机构的球坐标角动量，θ是机构的四元数形式的角动量，J是机构的质量转动惯量。

（ii）θdot = M^1(LLdot),其中θdot是机构的角动量偏导数，M是机构的质量转动惯量矩阵，Ldot是机构的球坐标角动量偏导数。

（iii）Ldot = J*ω,其中Ldot是机构的球坐标角动量偏导数，ω是机构的角速度，J是机构的质量转动惯量。

（iv）ωdot = M^1(Ldot-Lddot),其中ωdot是机构的角速度偏导数，M是机构的质量转动惯量矩阵，Lddot是机构的球坐标角动量二阶偏导数。

（v）Lddot = J*α,其中Lddot是机构的球坐标角动量二阶偏导数，α是机构的角加速度，J是机构的质量转动惯量。

球坐标角动量算符通常用来表示机构的旋转运动，可以帮助更好地理解机构的旋转状态，从而提高控制机构运动的能力。

- 1 -。

坐标、动量算符在彼此表象中的表示

（以一维情况为例：注意算符的表示形式和矩阵元形式）∫∫+++∞∞−=−=−εεδδ00)()()()()(000x x x f dx x x x f dx x x x f ***()()()(),()(1)()n n n x x x x δδδδ′′−=−−=−***注意上两式中的积分符号 在坐标表象：坐标算符：x; 动量算符: i x ∂−∂=（微分形式） ()()'"ˆˆ|||||'"'()'")(x x x xx dx x x x x x dx x x x x x x x x x δδδ′′′′′′=<>=<><=−>=−−∫∫ ① （将方框内部分视为函数()f x ，利用*式）()'"ˆ()()"'"()"'x x p x i x x x x d x x x d i x d δδδ∂⎛⎞−−⎜⎟∂∫⎝⎠=−=−== ② （利用** 式） ()d i x d x x δ=′′′′−−=（利用*** 式）（同曾谨言书的结果）动量表象：坐标算符：x i p ∂∂=（微分形式） ; 动量算符: p ()()'"ˆ()'(()"')""p p d i p p p dpd x dp p p i p d p δδδ=−=−−−∫== ③ （利用**式） ()p p d i p d δ′′=−′′= （利用*** 式）（同曾谨言书的结果） ()()'"ˆˆ()'""("')p p pdp p p p p p p p p δδδ=−⋅−=−∫ ④ （将方框内部分视为函数()f x ，利用*式）()())'"("""(")(')ˆ(""'p p p p p p i p p p dp d i p dp d i p p dp L z y y z y z z y p p x −∂∂−∂∂−=−−−=∫δδδ===4.1.求在动量表象中角动量x L 的矩阵元和2x L 的矩阵元。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
球坐标系的动量算符
在原子物理学和量子力学的教学中都会遇到动量算符，其表达
形式p =-inV,它是量子力学中的一个基本算符。它的的直角坐标
a , a , a 系下的形式为
i5
=
-
itt(i —
Bx
+J
—
函
+k —Bz )，各分量 九
=
a a -in — ，凡 = -iii — , 祁彻
仇 =-in. —a 是大家都熟悉的，学生们也没有疑惑，但是对于在球坐
az az ar az ae az J (Jl
ar r ae
我们
通
过直
角
坐标
系
可用e,<p
表
示出
.^l,
)l^.,
^K 在球面
坐标系
下的
形式：
oo ,,^l、
,^J
\ K^ J
f .g \ eo0sg,cspcoos0 coscp
= .gi
cos0 sin cp
c。
- sin0
一二rn
我们把上面的结果代入下式
2.2动量各分量的算符表示
2.2.1 - in —B 和
1 iii
a 不是厄密算符，不能作为动量的分量
祈
r汾
各分量的 P^,,^ Pa,^P叩算符形式就产生了疑惑，而一般的量子力学教材 [1~3]对此也没有过多说明，本文试图从在量子力学中表示力学量的
算符必须是厄密算符的要求出发解决这一疑惑。
1.直角坐标系中动量及其各分量的算符表示
P= -ihv'= -in(立； 十二＋立 k)= - in(~
函 By oz
OX
6
立
( ^ ＼ \ l．
、 、
-ay ^
o
丿·
z／
K＾
丿
P,和 p。的算符表示
一个算符F满足 F + = F ，才是厄密算符。量子力学中表示力学
量的算符必须是厄密的，而动量分量显然是力学量，所以表示动量
分量的算符必须是厄密算符。但是 -in —a 和 -in —1 —8 都不是厄密算
动量算符在直角坐标系下的表示为
i5
=
a -itz(t —
, +J
a —
+
, k
a —
)，
ax 初 az
对应的动量各分量的算符表示为 龙
=
-in
— a
,
, P
y
=
ox
-in — a , ft,
匈
=
- m—a ， oz
教学中使用比较多，结果也比较直接，一般学生没有疑惑。 2.球坐标系下动量及其各分量的算符表示 2.1球面坐标动量的算符表示 众所周知球面坐标与直角坐标的关系 x = rsin 8 cos<p, y = rsin 8 sin <p,z = rcos8
az
标下的动量算符整体形式
i5
=
-
in(—88r
. e'
+
- r1 扮8—乌rs＋ iIn0— 88cp
.e•)和动量
中，可以得到在球坐标系下，动量整体的算符表示
三+-»(立H二 十二仓 —a
p =-ihV = -iii(
1 6-80 -r
ar
仓
ar'r 汾 8 rsin 0 8q> 中）
e。
这样从直角坐标系演变而来，学生易于接受。
r = 扛 +y2 + z 2 ,t的 =2:'., cos8 =-=-=
z
x
r)x'+y2+z'
由此我们可得[1]
—i3 =— ar — a
+a—e
—i3
+J—(Jl —a =
sine
sin
(Jl
—a
1 +-cose
cos(Jl
— a s-in
— (Jl a
函 ox or 岔 oe OXO(J)
or r
=
—• r
p
或 P , =p • 一 r ，过渡到量子力学，由于 p和 r^不对易，为了保证径向 r
动量算符是厄密算符我们可以取
仇＝早 • 6 + 6 • _i:_) = -itz 立 ＿ 竺
2r
r
ar r
这才是动量径向分量的算符表示，它满足厄密性的要求。
同理，可以构造
九＝—I 他
•p
+p
• e。) =
祈
至于 -in l 8 ，我们也可以证明不是厄米算符。由于 r ae
乌= i cose cos<p + j cos e sin <p 一 ksin e 可知
-iii 丿 立= e0 • p =V cos0 cos<p + Jcos0 sin <p - k sin 叽(p) 十九丿＾ ＋仇k^)= r汾
同理得
^p
二
Z -r
=
Z -r
^p ” 』
i t" 2 + y2
r)
,
p^y
Y -r
__
- ^p x 2 3
由此我们可以求得
(-i飞］＝尸 =(分，五于］+
=p,~+ p)'~+ p, ~=U正~p, +~p,)-竺 =(?• 6J -琴 = -in詹－竺
*
- in—aar
所以 -
iii
—a 不是厄米算符。
r扫勹了
见
-
ifi
~
2+z 2x2 -y2
r飞 + y'fi
)z
尸了 p, +i1i2~勹
(,\. p)- iii rt的
=
一 in -1 — a - in 1 土一in-1 — a
r ae
rt的
r ae
a 故 一 in — r1 a—e 不是厄米算符。
2.2.2构造动量分力学中，径向动量就是动量的径向投影，定义为 p ,
户, cos0 cos<p + p） , cos0 sin <p - f,, sin九 0 = r,{xz亡x 了
+
zy ，石言了
P, y
-
勹＾
r P,
根据坐标和动量的对易关系我们可以求得：
｀尸 九z＝ x
zx
(y' + z'y' 王）Z
龙 -in r ' ~ ' + y 于
丸
zy
rj;言了
=
zy
r~
九
-in
~
2 +z 2x2- y 2)z
r' ~ ' +y于
丸
~
r
=
~
r
. p
,
+ili
zj;言了
r3
。
1a 所以 in r aa的共轭是
a~J ( -in ;
=
(e0
•
6J
=
九红十 r~
p'
rPz勹y 了
-p＾, ＄r 勹=
zx
r扫勹了
龙
-
ifi
0,' +z 沪 - x' 户 ~'+y于
)
+
zy
or
r ae
符，所以都不能作为动量分量的算符表示。
我们知道 - ;tz —i3 = —r • p，对任意波函数有，
or r
［气X ]'¥=气'¥- 仇（王'¥) = ;t, z' ~y' '¥
r
r
r
r
- 所以有
-X- ,-^rxp-=-ih
z2
+yr2
3X即得
^p x
X -r
=
rX- yP^x -ri y h zi 2 h + 3 y 2 2r+ yr
汾 rsin 0 o(Jl
—o
= —or —o +— 汾 —o + — Olp —o
=sine
sin
(Jl —o
I +-
cose
sin (Jl —o
+
COS(Jl
—o
彻匈 ar 函 ae 匈匈
ar r
茂 rsin 0 o(Jl
a ar a 汾 a 8qJ 8
a sine a
— = —— +—— +—— = cos0 —-—