第八章 无约束多维问题的最优化方法
- 格式:pptx
- 大小:563.19 KB
- 文档页数:42

多维无约束优化算法部门: xxx时间: xxx整理范文,仅供参考,可下载自行编辑多维无约束优化算法多维无约束优化问题的一般数学表达式为:求n 维设计变量使目标函数 多维无约束优化算法就是求解这类问题的方法,它是优化技术中最重要最基础的内容之一。
因为它不仅可以直接用来求解无约束优化问题,而且实际工程设计问题中的大量约束优化问题,有时也是通过对约束条件的适当处理,转化为无约束优化问题来求解的。
所以,无约束优化方法在工程优化设计中有着十分重要的作用。
b5E2RGbCAP 目前已研究出很多种无约束优化方法,它们的主要不同点在于构造搜索方向上的差别。
<1)间接法——要使用导数,如梯度法、<阻尼)牛顿法、变尺度法、共轭梯度法等。
<2)直接法——不使用导数信息,如坐标轮换法、鲍威尔法单纯形法等。
用直接法寻找极小点时,不必求函数的导数,只要计算目标函数值。
这类方法较适用于解决变量个数较少的<n ≤20)问题,一般情况下比间接法效率低。
间接法除要计算目标函数值外,还要计算目标函数的梯度,有的还要计算其海赛矩阵。
p1EanqFDPw各种优化方法之间的主要差异是在于构造的搜索方向,因此,搜索方向的构成问题乃是无约束优化方法的关键。
12[]T n x x x =x ()min f →x min ()nf R ∈x x 1(0,1,2,)k k k k s k α+=+=x x下面介绍几种经典的无约束优化方法。
1、梯度法基本思想:函数的负梯度方向是函数值在该点下降最快的方向。
将n 维问题转化为一系列沿负梯度方向用一维搜索方法寻优的问题,利用负梯度作为搜索方向,故称最速下降法或梯度法。
DXDiTa9E3d 搜索方向s 取该点的负梯度方向(最速下降方向> ,使函数值在该点附近的范围内下降最快 。
为了使目标函数值沿搜索方向能够获得最大的下降值,其步长因子应取一维搜索的最佳步长。
即有根据一元函数极值的必要条件和多元复合函数求导公式,得在最速下降法中,相邻两个迭代点上的函数梯度相互垂直。

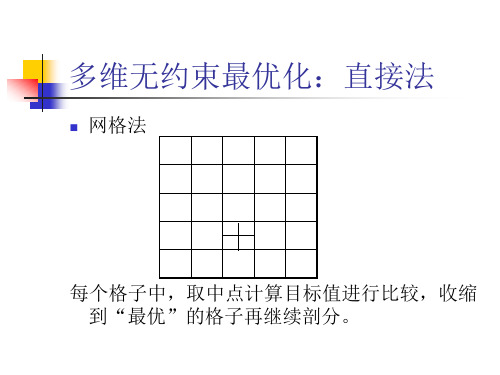



运筹学Operations Research无约束最优化方法西南交通大学经济管理学院§1.最速下降法§2.Newton法§3.共轭梯度法§4.变尺度法§5.直接法)()()()(0)(,,1,P o P X f X f P X f X f X f P E P T k k k k kn λλλ+∇+=+≠∇=∈非零:处的梯度它在是连续可微的函数即是单位向量设P X f o P X f X f P X f P f P X X f T k T k k k k)()()(lim )()(lim )(00∇=+∇=−+=∂∂→→λλλλλλλ的方向导数为:处关于方向在点k k k k T k kk T k X f P X f P X f P X f P P X f θθθcos )(cos )()()()(∇=⋅∇=∇∇∇之间的夹角,则和为。
记就是使下降最快的方向取最小的使处的最速下降方向。
在点通常把它叫做下降最快的方向。
出发使是从点时,上式最小,所以可知,当k kk k k X f f X X f P )(:−∇==πθ下降的搜索方向。
再去寻找使处不需要在点这时的点局部最优解的必要条件的已是满足的驻点。
是,则若f X X f X X f k k k k ,,)NP (0)(=∇:,)(,,,;,,,,,1的最佳步长,即作为点最小的确定使来的一维搜索即通过在负梯度方向上最佳步长方法采用振荡的情况。
所以一般在极值点附近出现来回则若步长选得大计算次数较多则收敛慢长选得小若步。
选择用固定步长时还要确定步长方向之后在选定了搜索得到下一个近似点为了由点+kk k k X X f X X λλ))((min ))((0kk k k k X f X f X f X f ∇−=∇−>λλλ§1.最速下降法)()()()()(0)()()()()())(()()()(21)()()())((2k k T k k T k k k k T k k T k k k k k T k kT k k k k X f X H X f X f X f X f X H X f X f X f d X f X df X f X H X f X f X f X f X f X f ∇∇∇∇==∇∇+∇−∇=∇−∇∇+∇∇−≈∇−λλλλλλλλ得:求导并令其等于零,则对§1.最速下降法Step1.。
多维无约束优化算法多维无约束优化问题的一般数学表达式为:求n 维设计变量使目标函数多维无约束优化算法就是求解这类问题的方法,它是优化技术中最重要最基础的内容之一。
因为它不仅可以直接用来求解无约束优化问题,而且实际工程设计问题中的大量约束优化问题,有时也是通过对约束条件的适当处理,转化为无约束优化问题来求解的。
所以,无约束优化方法在工程优化设计中有着十分重要的作用。
目前已研究出很多种无约束优化方法,它们的主要不同点在于构造搜索方向上的差别。
(1)间接法——要使用导数,如梯度法、(阻尼)牛顿法、变尺度法、共轭梯度法等。
(2)直接法——不使用导数信息,如坐标轮换法、鲍威尔法单纯形法等。
用直接法寻找极小点时,不必求函数的导数,只要计算目标函数值。
这类方法较适用于解决变量个数较少的(n ≤20)问题,一般情况下比间接法效率低。
间接法除要计算目标函数值外,还要计算目标函数的梯度,有的还要计算其海赛矩阵。
各种优化方法之间的主要差异是在于构造的搜索方向,因此,搜索方向的构成问题乃是无约束优化方法的关键。
下面介绍几种经典的无约束优化方法。
1、梯度法基本思想:函数的负梯度方向是函数值在该点下降最快的方向。
将n 维问题转化为一系列沿负梯度方向用一维搜索方法寻优的问题,利用负梯度作为搜索方向,故称最速下降法或梯度法。
搜索方向s 取该点的负梯度方向(最速下降方向) ,使函数值在该点附近的范围内下降最快 。
为了使目标函数值沿搜索方向能够获得最大的下降值,其步长因子应取一维搜索的最佳步长。
即有12[]T n x x x = x ()min f →x ()k f -∇x k αmin ()nf R ∈x x 1(0,1,2,)k k k k s k α+=+= x x 1(0,1,2,)k k kk s k α+=+= x x 1()(0,1,2,)k k k k a f k +=-∇= x x x 1()[()]min [()]min ()k k k k k k k a af f a f f a f ϕα+=-∇=-∇=x x x x x根据一元函数极值的必要条件和多元复合函数求导公式,得在最速下降法中,相邻两个迭代点上的函数梯度相互垂直。
多维无约束优化算法多维无约束优化问题的一般数学表达式为:求n 维设计变量使目标函数多维无约束优化算法就是求解这类问题的方法,它是优化技术中最重要最基础的内容之一。
因为它不仅可以直接用来求解无约束优化问题,而且实际工程设计问题中的大量约束优化问题,有时也是通过对约束条件的适当处理,转化为无约束优化问题来求解的。
所以,无约束优化方法在工程优化设计中有着十分重要的作用。
目前已研究出很多种无约束优化方法,它们的主要不同点在于构造搜索方向上的差别。
(1)间接法——要使用导数,如梯度法、(阻尼)牛顿法、变尺度法、共轭梯度法等。
(2)直接法——不使用导数信息,如坐标轮换法、鲍威尔法单纯形法等。
用直接法寻找极小点时,不必求函数的导数,只要计算目标函数值。
这类方法较适用于解决变量个数较少的(n ≤20)问题,一般情况下比间接法效率低。
间接法除要计算目标函数值外,还要计算目标函数的梯度,有的还要计算其海赛矩阵。
各种优化方法之间的主要差异是在于构造的搜索方向,因此,搜索方向的构成问题乃是无约束优化方法的关键。
下面介绍几种经典的无约束优化方法。
1、梯度法基本思想:函数的负梯度方向是函数值在该点下降最快的方向。
将n 维问题转化为一系列沿负梯度方向用一维搜索方法寻优的问题,利用负梯度作为搜索方向,故称最速下降法或梯度法。
搜索方向s 取该点的负梯度方向(最速下降方向) ,使函数值在该点附近的范围内下降最快 。
为了使目标函数值沿搜索方向能够获得最大的下降值,其步长因子应取一维搜索的最佳步长。
即有12[]T n x x x = x ()min f →x ()k f -∇x k αmin ()nf R ∈x x 1(0,1,2,)k k k k s k α+=+= x x 1(0,1,2,)k k k k s k α+=+= x x 1()(0,1,2,)k k k k a f k +=-∇= x x x 1()[()]min [()]min ()k k k k k k k a af f a f f a f ϕα+=-∇=-∇=x x x x x根据一元函数极值的必要条件和多元复合函数求导公式,得在最速下降法中,相邻两个迭代点上的函数梯度相互垂直。