平抛运动中的典型问题

平抛运动临界问题平抛运动是指一个物体在不受外力影响下，沿着一个水平方向进行抛掷的运动。

在平抛运动中，物体受到重力的作用而向下做加速运动，而在水平方向上则保持匀速直线运动。

当物体的初速度和抛掷角度确定时，我们可以通过解析的方法来求解物体的最大高度、最大飞行距离以及落地处的速度等问题。

问题描述一个足球运动员以θ的角度用力将足球从地面上以v0的初速度抛出。

为了使足球能够在某一距离d处接触地面，求抛出足球时的最小速度v0。

解题思路根据平抛运动的基本公式，可以得到足球在竖直方向的运动方程为：ℎ=v0sinθt−gt2 2其中，ℎ是足球抛出后的最大高度，g是重力加速度，t是足球从抛出到落地所需的时间。

当足球接触地面时，ℎ的值为0，即：0=v0sinθt−gt22 ⇒ v0sinθt=gt22将t表示为：t=2v0sinθg代入求解接触地面的位置d与时间t的关系：d=v0cosθ⋅t ⇒ d=v0cosθ⋅2v0sinθg化简得到：d=2v02sinθ⋅cosθg将上述方程转化为关于v0的二次方程形式：v02sin2θ−gd2=0解二次方程，并根据物理意义得到一个物理解：v 0=√gd 2sin2θ该解即为足球抛出时的最小速度。

示例计算假设 d =50 m ，θ=45∘，g =9.8 m/s²，代入上述公式可得：v 0=√9.8×502sin90∘≈22.142≈11.07 m/s 因此，足球抛出时的最小速度为约 11.07 m/s 。

总结本文使用物理学中的平抛运动公式，通过计算和代数运算的方法，解决了一个关于平抛运动临界问题的例题。

通过该例题，我们了解到通过解析方法可以推导出平抛运动的高度和水平距离与初速度和抛射角度之间的关系，并使用这个关系来解决实际问题。

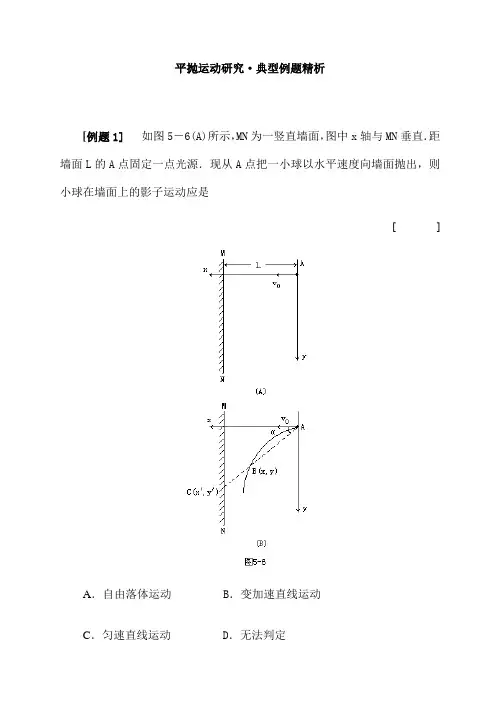
平抛运动研究·典型例题精析[例题1] 如图5－6(A)所示，MN为一竖直墙面，图中x轴与MN垂直．距墙面L的A点固定一点光源．现从A点把一小球以水平速度向墙面抛出，则小球在墙面上的影子运动应是[]A．自由落体运动 B．变加速直线运动C．匀速直线运动 D．无法判定[思路点拨] 小球抛出后为平抛运动，在图中x方向上为匀速直线运动，在y方向上为自由落体运动．故不少同学选择(A)项，而实际上该答案是错误的．问题在于我们研究的并不是小球在竖直方向上的运动，而是在点光源照射下小球在墙上影子的运动．[解题过程] 设小球从A点抛出后经过时间t，其位置B坐标为(x，y)，连接AB并延长交墙面于C(x′，y′)．显然C点就是此时刻小球影子的位置(如图5－6(B)所示)．令AB与x轴夹角为α，则依几何关系，影子位置y′＝L·tanα．故令 gL/2v0＝k，则y′＝k·t．即影子纵坐标y′与时间t是正比例关系，所以该运动为匀速直线运动，应选(C)项．[小结] (1)要认真审清题意：本题所研究的是“点光源照射下小球影子的运动”，否则会差之毫厘，谬之千里．(2)对选择题的分析判断，切莫主观猜测，要做到弃之有理，选之有据．对于需做出定量研究的问题，最好的方法就是将物理图景利用数学语言表达出来，例如在本题中就是写出位移随时间的函数关系．[例题2] 如图5－7所示，M和N是两块相互平行的光滑竖直弹性板．两板之间的距离为L，高度为H．现从M板的顶端O以垂直板面的水平速度v0抛出一个小球．小球在飞行中与M板和N板，分别在A点和B点相碰，并最终在两板间的中点C处落地．求：(1)小球抛出的速度v0与L和H之间满足的关系；(2)OA、AB、BC在竖直方向上距离之比．[思路点拨] 根据平抛运动规律，建立小球在MN之间的运动图景是本题关键之一．小球被水平抛出后，如果没有板面N的作用，其运动轨迹应如图5－8中虚线所示．由于板面光滑弹性良好，故在A点与N板碰后，应满足反射定律，反弹后运动轨迹与虚线，满足以N板为轴的左右对称．第二次在B点与M板相碰情况亦然．本题的另一难点是问题竖直方向运动为自由落体，所以不少同学会认为这三段在竖直方向上距离之比应为：1∶3∶2.5．你是否也有同样的结果呢？[解题过程] (1)分析可知运动的全过程中，小球始终保持其水平速度大小v0不变．设运动全过程飞行时间为t，水平全程长度为S，则又 S＝2.5L，(2)取小球由B到C为一个时间间隔Δt．小球从O抛出到C点落地共经过5个Δt．在此5个Δt中下落高度之比为：1∶3∶5∶7∶9．由于t OA包括第1个Δt和第2个Δt；t AB包括第3个Δt和第4个Δt，故三段竖直距离之比为h OA∶h AB∶h BC＝(1＋3)∶(5＋7)∶9＝4∶12∶9．[小结] (1)注意将平抛运动的一般规律与题目中特定物理条件相结合，才能正确描述题目的物理图景。

[例1] 在倾角为的斜面上的P点，以水平速度向斜面下方抛出一个物体，落在斜面上的Q点，证明落在Q点物体速度。

解析：设物体由抛出点P运动到斜面上的Q点的位移是，所用时间为，则由“分解位移法”可得，竖直方向上的位移为；水平方向上的位移为。

又根据运动学的规律可得竖直方向上，水平方向上，所以Q点的速度[例2] 如图3所示，在坡度一定的斜面顶点以大小相同的速度同时水平向左与水平向右抛出两个小球A和B，两侧斜坡的倾角分别为和，小球均落在坡面上，若不计空气阻力，则A 和B两小球的运动时间之比为多少？图3解析：和都是物体落在斜面上后，位移与水平方向的夹角，则运用分解位移的方法可以得到所以有同理则[例3] 如图6所示，在倾角为的斜面上以速度水平抛出一小球，该斜面足够长，则从抛出开始计时，经过多长时间小球离开斜面的距离的达到最大，最大距离为多少？图6解析：将平抛运动分解为沿斜面向下和垂直斜面向上的分运动，虽然分运动比较复杂一些，但易将物体离斜面距离达到最大的物理本质凸显出来。

取沿斜面向下为轴的正方向，垂直斜面向上为轴的正方向，如图6所示，在轴上，小球做初速度为、加速度为的匀变速直线运动，所以有① ②当时，小球在轴上运动到最高点，即小球离开斜面的距离达到最大。

由①式可得小球离开斜面的最大距离当时，小球在轴上运动到最高点，它所用的时间就是小球从抛出运动到离开斜面最大距离的时间。

由②式可得小球运动的时间为例4：在平直轨道上以20.5/m s 的加速度匀加速行驶的火车上，相继下落两个物体下落的高度都是2.45m ．间隔时间为1s ．两物体落地点的间隔是2.6m ，则当第一个物体下落时火车的速度是多大？（g 取210/m s ）分析：如图所示．第一个物体下落以0v 的速度作平抛运动，水平位移0s ，火车加速到下落第二个物体时，已行驶距离1s ．第二个物体以1v 的速度作平抛运动水平位移2s ．两物体落地点的间隔是2.6m ．解：由位置关系得 1202.6s s s =+-物体平抛运动的时间 20.7ht s g'=00021002000.710.252()(0.5)0.7s v t v s v t at v s v at t v '===+=+'=+⋅=+⨯由以上三式可得201sin 22sin 2/L gt L t gv m sαα===例5：光滑斜面倾角为θ，长为L ，上端一小球沿斜面水平方向以速度0v 抛出（如图所示），小球滑到底端时，水平方向位移多大？解：小球运动是合运动，小球在水平方向作匀速直线运动，有0s v t = ①沿斜面向下是做初速度为零的匀加速直线运动，有212L at =② 根据牛顿第二定律列方程sin mg ma θ= ③由①，②，③式解得0022sin L Ls v v a g θ==例6：某一物体以一定的初速度水平抛出，在某1s 内其速度方向与水平方向成37︒变成53︒，则此物体初速度大小是________/m s ，此物体在1s 内下落的高度是________m （g 取210/m s ） 选题目的：考查平抛物体的运动知识的灵活运用．解析：作出速度矢量图如图所示，其中1v ．2v 分别是ts 及(1)t s +时刻的瞬时速度．在这两个时刻，物体在竖直方向的速度大小分别为gt 及(1)g t +，由矢量图可知：037gt v tg =︒ 0(1)53g t v tg +=︒由以上两式解得017.1/v m s = 97t s =物体在这1s 内下落的高度2211(1)22y g t gt ∆=+- 221919(1)()2727g g =+-17.9m =例7如图，跳台滑雪运动员经过一段加速滑行后从O 点水平飞出，经过3.0s 落到斜坡上的A 点．已知O 点是斜坡的起点，斜坡与水平面的夹角θ=37°，运动员的质量m=50kg ．不计空气阻力．（取sin37°=0.60，cos37°=0.80；g 取10m/s 2）求：（1）A 点与O 点的距离L ；（2）运动员离开O 点时的速度大小；（1）从O点水平飞出后，人做平抛运动，根据水平方向上的匀速直线运动，竖直方向上的自由落体运动可以求得A点与O点的距离L；（2）运动员离开O点时的速度就是平抛初速度的大小，根据水平方向上匀速直线运动可以求得；设A点与O点的距离为L，运动员在竖直方向做自由落体运动，则有：Lsin37°=0.5gt2L=gt22sin37°=75m（2）设运动员离开O点的速度为v0，运动员在水平方向做匀速直线运动，即：Lcos37°=v0t解得：v0=20m/s答：（1）A点与O点的距离是75m；（2）运动员离开O点时的速度大小是20m/s．1：在倾角为的斜面上的P点，以水平速度向斜面下方抛出一个物体，落在斜面上的Q点，证明落在Q点物体速度。

平抛运动典型例题
1.从某高处以6m/s的初速度、30°抛射角斜向上方抛出一石子，落地时石子的速度方向和水平线的夹角为60°，求石子在空中运动的时间和抛出点离地面的高度。

（取g=10m/s2）
2.如图,可视为质点的小球,位于半径为半圆柱体左端点A的正上方某处,以一定的初速度水平抛出小球,其运动轨迹恰好能与半圆柱体相切于B点.过B点的半圆柱体半径与水平方向的夹角为,则初速度为:(不计空气阻力,重力加速度为多少。

3.如图所示，在倾角为45O 的斜面底端正上方高H=6.4m 处，将一小球以不同初速度水平抛出，若小球到达斜面时位移最小，重力加速度g=10m/s 2，求：
（1）小球平抛的初速度；
（2）小球落到斜面时的速度。

4如图所示，装甲车在水平地面上以速度s m v /200=沿直线前进，车上机枪的枪管水平，距地面高为h=1.8m 。

在车正前方竖直立一块高为两米的长方形靶，其底边与地面接触。

枪口与靶距离为时，机枪手正对靶射出第一发子弹，子弹相对于枪口的初速度为s m v /800=。

在子弹射出的同时，装甲车开始匀减速运动，行进s=90m 后停下。

装甲车停下后，机枪手以相同方式射出第二发子弹。

（不计空气阻力，子弹看成质点，重力加速度
）
（1）求装甲车匀减速运动时的加速度大小；
（2）当410m 时，求第一发子弹的弹孔离地的高度，并计算靶上两个弹孔之间的距离；
（3）若靶上只有一个弹孔，求L 的范围。

处越过A的壕沟，沟面如图1所示，某人骑摩托车在水平道路上行驶，要在[例1]，摩托车的速度至少要有多大？对面比A处低图1解析：在竖直方向上，摩托车越过壕沟经历的时间在水平方向上，摩托车能越过壕沟的速度至少为2. 从分解速度的角度进行解题对于一个做平抛运动的物体来说，如果知道了某一时刻的速度方向，则我们常常是“从分解速度”的角度来研究问题。

[例2] 如图2甲所示，以9.8m/s的初速度水平抛出的物体，飞行一段时间后，垂直地撞在为的斜面上。

可知物体完成这段飞行的时间是（倾角）D.B.A.C.图2和竖直分速度（如图解析：2先将物体的末速度乙所示）。

分解为水平分速度根据平抛运动的分解可知物体水平方向的初速度是始终不变的，所以；又因为与间的夹角等于斜面的倾角与水平面垂直，所以。

再根据平抛运动的斜面垂直、与分解可知物体在竖直方向做自由落体运动，那么我们根据了。

则就可以求出时间所以根据平抛运动竖直方向是自由落体运动可以写出所以所以答案为C。

3. 从分解位移的角度进行解题对于一个做平抛运动的物体来说，如果知道了某一时刻的位移方向（如物体从已知倾角的斜面上水平抛出，这个倾角也等于位移与水平方向之间的夹角），则我们可以把位移分解成水平方向和竖直方向，然后运用平抛运动的运动规律来进行研究问题（这种方法，暂且叫做“分解位移法”）点，以水平速度向斜面下方抛出一个物体，落在斜面上在倾角为的斜面上的P[例3]点物体速度Q的Q点，证明落在。

，所用时间为点的位移是P运动到斜面上的Q，则由“分解设物体由抛出点解析：位移法”可得，竖直方向上的位移为；水平方向上的位移为。

又根据运动学的规律可得，竖直方向上水平方向上，则点的速度所以Q所示，在坡度一定的斜面顶点以大小相同的速度同时水平向左与水平向右4] 如图3[例，小球均落在坡面上，两侧斜坡的倾角分别为若不计空气和，抛出两个小球A和B 两小球的运动时间之比为多少？B阻力，则A和图3和都是物体落在斜面上后，解析：位移与水平方向的夹角，则运用分解位移的方法可以得到所以有．同理则4. 从竖直方向是自由落体运动的角度出发求解在研究平抛运动的实验中，由于实验的不规范，有许多同学作出的平抛运动的轨迹，常常不能直接找到运动的起点（这种轨迹，我们暂且叫做“残缺轨迹”），这给求平抛运动的初速度带来了很大的困难。

平抛运动专题复习一、平抛运动规律复习二、平抛运动常见问题归纳1、飞机投弹类问题例1将一个小球以初速度v0水平抛出，落地时速度为vt，空气阻力不计，求：(1) 小球在空中飞行的时间；(2) 抛出点到地面的高度；(3) 水平射程；(4) 小球的位移。

例2如图所示，在一次地空演习中，离地H高处的飞机发射一颗炮弹，炮弹以水平速度v1飞出欲轰炸地面目标P，反应灵敏的地面拦截系统同时以速度v2竖直向上发射导弹进行拦截。

设飞机发射炮弹时与拦截系统的水平距离为s，若拦截成功，不计空气阻力，则v1、v2的关系应满足A．v1=v2B．v1= c. v1＝v2xH D．v1=2、斜面上的平抛运动例3如图所示，以10m/s的水平初速度v0抛出的物体，飞行一段时间后，垂直地撞在倾角θ为30°的斜面上，可知物体完成这段飞行的时间是( ) （g=10m/s2）s B．s C．s D．2s例4如图3所示，在坡度一定的斜面顶点以大小相同的速度v同时水平向左与水平向右抛出两个小球A和B，两侧斜坡的倾角分别为︒37和︒53，小球均落在坡面上，若不计空气阻力，则A和B两小球的运动时间之比为多少？3、与平抛运动有关的临界问题例5如图所示，水平屋顶高H＝5 m，墙高h＝3.2 m，墙到房子的距离L＝3 m，墙外马路宽D＝10 m，小球从屋顶水平飞出落在墙外的马路上，求小球离开屋顶时的速度v应该满足什么条件？(g＝10 m/s2)例6一带有乒乓球发射机的乒乓球台如图所示。

水平台面的长和宽分别为L1、L2，中间球网高度为h。

发射机安装于台面左侧边缘的中点，能以不同速率向右侧不同方向水平发射乒乓球，发射点距台面高度为3h。

不计空气的作用，重力加速度大小为g。

若乒乓球的发射速率v在某范围内，通过选择合适的方向，就能使乒乓球落到球网右侧台面上，则v的最大取值范围是4、类平抛运动问题例7如图6—4—21所示，有一倾角为30°的光滑斜面，斜面长L为10m，一小球从斜面顶端以10m/s的速度沿水平方向抛出，求：（1）小球沿斜面滑到底端时水平位移s；（2）小球到达斜面底端时的速度大小。

平抛运动的经典例题
1.一个小球以10m/s的初速度从距离地面15m高的地方平抛，求小球在水平方向上的运动时间和落点的高度。

解：小球在水平方向上做匀速直线运动，其速度vx=10m/s，方向水平向右。

小球在垂直方向上做自由落体运动，其速度
vy=gt=10m/s×2=20m/s，方向竖直向下。

由平抛运动的解析公式可知，水平位移
x=vx*t=10m/s×4s=40m，垂直位移
y=1/2gt^2=1/2×20m/s×4s=80m。

落点高度h=y-x=80m-40m=40m。

2.一个小球以10m/s的初速度从距离地面15m高的地方平抛，求小球到达地面时，竖直方向上的速度大小和方向。

解：小球在垂直方向上做自由落体运动，其速度
vy=gt=10m/s×2=20m/s，方向竖直向下。

小球到达地面时，速度为0，因此竖直方向上的速度大小为
20m/s，方向竖直向下。

3.一个小球以10m/s的初速度从距离地面20m高的地方平抛，求小球到达地面时，竖直方向上的速度大小和方向。

解：小球在垂直方向上做自由落体运动，其速度
vy=gt=10m/s×2=20m/s，方向竖直向下。

小球到达地面时，速度为0，因此竖直方向上的速度大小为
20m/s，方向竖直向下。

平抛运动1．常规题的解法【例题】如图所示，墙壁上落有两只飞镖，它们是从同一位置水平射出的，飞镖A 与竖直墙壁成530角，飞镖B 与竖直墙壁成370角，两者相距为d ，假设飞镖的运动是平抛运动，求射出点离墙壁的水平距离?(sin370=0.6，cos370＝0.8)★解析：设射出点离墙壁的水平距离为s ，A 下降的高度h 1，B 下降的高度h 2，根据平抛运动规律可知：（根据反向沿长线是中点）︒=53tan 21s h ︒=37tan 22sh答案：724ds =知识链接：本题的关键是理解箭头指向的含义——箭头指向代表这一时刻速度的方向，而不是平抛物体的位移方向。

理解两个重要的推论：推论1：做平抛(或类平抛)运动的物体在任一时刻任一位置处，设其末速度方向与水平方向的夹角为θ，位移与水平方向的夹角为α，则tanθ=2tanα推论2：做平抛(或类平抛)运动的物体任意时刻的瞬时速度的反向延长线一定通过此时水平位移的中点。

2．斜面问题 （1）分解速度【例题】如图所示，以水平初速度0v 抛出的物体，飞行一段时间后，垂直撞在倾角为θ的斜面上，求物体完成这段飞行的时间和位移。

★解析：gtv v v y x 0tan ==θ（分解速度），∴θtan 0⋅=g v tθθθθ222002tan 2)1tan 2(tan 21tan g v t v gt S S S x y +=⋅+=⋅+=上面的S 好象不对我做θθ222022tan 2tan 41g v y x S +=+=【例题】如图所示，在倾角为370的斜面底端的正上方H 处，平抛一小球，该小球垂直打在斜面上的一点，求小球抛出时的初速度。

★解析：小球水平位移为0x v t = 竖直位移为212y gt =由图可知，20012tan 37H gt v t-=， 又0tan 37v gt=（分解速度），消去t 解之得： 015317gHv =（2）分解位移【例题】在倾角为θ的斜面顶端A 处以速度0v 水平抛出一小球，落在斜面上的某一点B 处，设空气阻力不计，求(1)小球从A 运动到B 处所需的时间和位移。

高中物理：平抛运动习题及详解平抛运动可以看成是水平方向做匀速运动，竖直方向做自由落体运动的这两种运动的合运动。

解决问题的方法是：根据题意，正确地作出示意图，识别出运动性质后，将平抛运动分解成直线运动，运用相关的运动规律（公式），列出方程解出结果。

一、运用平抛运动规律解题例1、如图1所示，两个相对的斜面，倾角分别为37°和53°。

在顶点把两个小球以同样大小的初速度分别向左、右水平抛出，小球都落在斜面上。

若不计空气阻力，则A、B两个小球的运动时间之比为（）。

A. 1：1B. 4：3C. 16：9D. 9：16图1解析：设作平抛运动物体运动的时间为t，则位移的水平分量和竖直分量分别为而由图可知故所以有即D选项正确。

二、平抛运动问题正误辨析例2、如图2所示，AB为斜面，BC为水平面。

从A点以水平速度v向右抛出一小球，其落点与A的水平距离为S1；从A点以水平速度2v向右抛出另一小球，其落点与A 的水平距离为S2。

不计空气阻力，则S1：S2可能为（）。

图2A. 1：2B. 1：3C. 1：4D. 1：5分析：根据平抛运动的基本公式可推得水平位移与初速度成正比，所以误认为选项A正确。

此题对选项B的判断用到临界法，确定了两种情况平抛运动的解，介于两者之间的也是符合题意的解。

不要忽略了落点在斜面上的情况。

解：要考虑到落至斜面和落至平面上的不同情况。

若两次都落在平面上，则A对；若两次都落在斜面上，则C对；若第一次落在斜面上，第二次落在平面上，B就可能正确，其实只要介于1：2和1：4之间都可以，所以正确选项应为A、B、C。

例3、如图3所示，一高度为的水平面在A点处与一倾角为θ＝30°的面连接。

一小球以的速度在平面向右运动。

求小球从A点运动到地面所需要的时间（平面与斜面均光滑，取）。

图3某同学对此题的解法为：小球沿斜面运动，则由此可求得落地的时间t。

问：你同意上述解法吗？若同意，求出所需要的时间；若不同意，则说明理由并求出你认为正确的结果。

平抛运动临界问题、相遇问题、类平抛运和斜抛运动导练目标导练内容目标1平抛运动临界问题目标2平抛运动中的相遇问题目标3类平抛运动目标4斜抛运动【知识导学与典例导练】一、平抛运动临界问题擦网压线既擦网又压线由H−h=12gt2=12gx1v12得：v1=x1g2H−h由H=12gt2=12gx1+x2v22得：v2=x1+x2g2H由H−h=12gt2=12gx1v02和H=12gt2=12gx1+x2v02得：H−hH=x21x1+x221某天，小陈同学放学经过一座石拱桥，他在桥顶A处无意中把一颗小石子水平沿桥面向前踢出，他惊讶地发现小石子竟然几乎贴着桥面一直飞到桥的底端D处，但是又始终没有与桥面接触。

他一下子来了兴趣，跑上跑下量出了桥顶高OA=3.2m，桥顶到桥底的水平距离OD=6.4m。

这时小陈起一颗小石，在A 处，试着水平抛出小石头，欲击中桥面上两块石板的接缝B处(B点的正下方B′是OD的中点)，小陈目测小石头抛出点离A点高度为1.65m，下列说法正确的是()A.石拱桥为圆弧形石拱桥B.小陈踢出的小石头速度约为6.4m/sC.小陈抛出的小石头速度约为4.6m/sD.先后两颗小石子在空中的运动时间之比为2:1二、平抛运动中的相遇问题平抛与自由落体相遇水平位移：l=vt空中相遇：t<2hg平抛与平抛相遇（1）若等高(h1=h2)，两球同时抛；（2）若不等高(h1>h2)两球不同时抛，甲球先抛；（3）位移关系：x1+x2=L（1）A球先抛；（2）t A>t B；(3)v0A<v0B（1）A、B两球同时抛；(2)t A=t B；(3)v0A>v0B平抛与竖直上抛相遇（1）L=v1t；（2）12gt2+v2t−12gt2=h⇒t=hv2；（3）若在S2球上升时两球相遇，临界条件：t<v2g，即：hv2<v2g，解得：v2>gh；（4）若在S2球下降时两球相遇，临界条件：v2g<t< 2v2g，即v2g<hv2<2v2g，解得：gh2<v2<gh平抛与斜上抛相遇(1)v1t+v2cosθ⋅t=L；(2)12gt2+v2sinθt−12gt2=h⇒t=hv2sinθ；(3)若在S2球上升时两球相遇，临界条件：t<v 2sin θg ，即：hv 2sin θ<v 2sin θg ，解得：v 2>ghsin θ；(4)若在S 2球下降时两球相遇，临界条件：v 2sin θg <t <2v 2sin θg，即v 2sin θg <h v 2sin θ<2v 2sin θg ，解得：gh2sin θ<v 2<gh sin θ1如图所示，相距l 的两小球A 、B 位于同一高度h (l 、h 均为定值)。

5.2平抛运动典型例题分析题型一、平抛运动与科技实践相结合例1、某卡车司机在限速60km/h的公路上因疲劳驾驶而使汽车与路旁的障碍物相撞。

处理事故的警察在路旁的泥地中发现了卡车顶上的一个金属零件，可以判断，这是事故发生时该零件从车顶松脱后被抛出而陷在泥地里的。

警察测得该零件原位置与陷落点的水平距离为13.3m，车顶距泥地的竖起高度为 2.45m.请你根据这些数据来判断该车是否超速？（g=9.8m/s2）拓展：一水平放置的水管，距地面高h＝l.8m，管内横截面积S＝2.0cm2。

有水从管口处以不变的速度v＝2.0m/s源源不断地沿水平方向射出，设出口处横截面上各处水的速度都相同，并假设水流在空中不散开。

取重力加速度g＝10m／s2，不计空气阻力。

求水流稳定后在空中有多少立方米的水。

题型二、平抛运动与斜面结合的问题倾角为θ=300的斜面上,则可知小球的飞行时间是（）A．3/3B．23/3C．3D．2拓展：如图，在倾角为α的斜面上A点，以初速度v0水平抛出小球，小球落在斜面上的B点，不计空气阻力，求小球运动时间多长？落到B点的速度多大？题型三、平抛运动中的相遇问题例3、一艘敌舰正以V 1=40m/s 的速度逃跑，执行追击任务的飞机，在距水面高度h=320m 的水平面上以速度V 2=105m/s 同向飞行，未击中敌舰。

应“提前”投弹，若空气的阻力可以不计，重力加速度g=10m/s 2，飞机投弹时沿水平方向，则投弹时它与敌舰之间的水平距离应为多大？若投弹后飞机仍以原来的速度飞行，在炸弹击中敌舰时，飞机与敌舰的位置时怎样的？拓展：如图所示，在一次空地演习中，离地H 高处的飞机以水平速度，v 1 发射一颗炮弹欲轰炸地面目标P ，反应灵敏的地面拦截系统同时以速度v 2 竖直向上发射炮弹拦截．设拦截系统与飞机的水平距离为s ，若拦截成功，不计空气阻力，则v 1、v 2的关系应满足（ ）A.v 1=v 2B.v 1=H sv 2 C.v 1=H s v 2 D.v 1=s Hv 2题型四、类平抛运动的处理例4、如图所示，光滑斜面长为a ，宽为b ，倾角为θ。