(word完整版)高中函数典型例题.doc

高 中 数 学 函 数 的 凸 凹 性 例 讲山西忻州五寨一中 摄爱忠函数凹凸性问题是高考中的一种新题型．这种题情景新颖、背景公平，能考查学生的创新能力和潜在的数学素质.①掌握增量法解决凹凸曲线问题 ②函数的凹凸性定义及图像特征一、凸凹函数定义：设函数f 为定义在区间I 上的函数，若对（b a ,）上任意两点1x 、2x ，恒有：（1）1212()()()22x x f x f x f ++<，则称f 为（b a ,）上的下凸函数； （2）1212()()()22x x f x f x f ++>，则称f 为（b a ,）上的上凸函数。

二、凹凸函数的几何特征：1.形状特征图1（下凸函数） 图2（上凸函数）下凸函数的形状特征是：其函数曲线任意两点1A 与2A 之间的部分位于弦21A A 的下方;上凸函数的形状特征是：其函数曲线任意两点1A 与2A 之间的部分位于弦21A A 的上方。

2切线斜率特征图3（下凸函数） 图4（上凸函数）下凸函数的切线斜率特征是：切线的斜率)(x f y =随x 增大而增大；上凸函数的切线斜率特征是：切线的斜率)(x f y =随x 增大而减小； 简记为：斜率凹增凸减．．．．．．。

3增量特征：图5（下凸函数） 图6（凸函数）下凸函数的增量特征是：i y ∆越来越大；上凸函数的增量特征是：i y ∆越来越小； 简记为：增量下大上小．．．．．．。

弄清了上述两类凸函数及其图象的本质区别和变化的规律，就可准确迅速、简捷明了地解决有关凸的曲线问题． 三、凸函数与导数的关系定理1（可导函数与凹凸函数的等价命题）：（1） 设)(x f 为区间I 上的可导函数,则：)(x f 为I 上的下凸函数⇔)(x f '为I 上的增函数；（2） 设)(x f 为区间I 上的可导函数,则：)(x f 为I 上的上凸函数⇔)(/x f 为I 上的减函数；定理2（可导函数与二阶导数的关系）：（1）设)(x f 为区间I 上的可导函数,则：)(x f 为I 上的下凸函数⇔0)(≥''x f 且)(x f ''不在I 上的任一子区间上恒为零.（2）设)(x f 为区间I 上的可导函数,则：)(x f 为I 上的上凸函数⇔0)(≤''x f 且)(x f ''不在I 上的任一子区间上恒为零.四、函数凹凸性的应用题型1：图形与图像问题◇题目：一高为Ｈ满缸水量为Ｖ的鱼缸的截面如图7所示，其底部碰了一个小洞，满缸水从洞中流出．若鱼缸水深为ｈ时水的体积为Ｖ，则函数)(h f V =的大致图象可能是图8中的（ ）．解：据四个选项提供的信息（ｈ从Ｏ→Ｈ），我们可将水“流出”设想成“流入”，这样，每当ｈ增加一个单位增量Δｈ时，根据鱼缸形状可知V 的变化开始其增量越来越大，但经过中截面后则越来越小，故Ｖ关于ｈ的函数图象是先凹后凸的，因此，选Ｂ．练一练：◇题目：向高为Ｈ的水瓶中注水，注满为止，如果注水量V 与水深ｈ的函数关系的图象如图9所示，那么水瓶的形状是（图10中的）图7图8（）．（1998年全国高考题）图9 图10解：因为容器中总的水量（即注水量）V关于ｈ的函数图象是凸的，即每当ｈ增加一个单位增量Δｈ，V 的相应增量ΔＶ越来越小．这说明容器的上升的液面越来越小，故选Ｂ．讲一讲：◇题目：在某种金属材料的耐高温实验中，温度随着时间变化的情况由微机记录后再显示的图象如下图所示．现给出下面说法：①前5分钟温度增加的速度越来越快；②前5分钟温度增加的速度越来越慢；③5分钟以后温度保持匀速增加；④5分钟以后温度保持不变．其中正确的说法是（）．Ａ．①④Ｂ．②④Ｃ．②③Ｄ．①③解：因为温度ｙ关于时间ｔ的图象是先上凸后平行直线，即5分钟前每当ｔ增加一个单位增量Δｔ，则ｙ相应的增量Δｙ越来越小，而5分钟后是ｙ关于ｔ的增量保持为0，故选Ｂ．注：本题也选自《中学数学教学参考》2001年第1～2合期的《试题集绵》，用了增量法就反成了“看图说画”．练一练：◇题目：（06重庆理）如下图所示，单位圆中弧AB的长为x，f(x)表示弧AB与弦AB所围成的弓形面积的２倍，则函数y=f(x)的图象是（）C图17解：易得弓形AxB的面积的2倍为f(x)=ｘ-sinｘ．由于ｙ１＝ｘ是直线，每当ｘ增加一个单位增量Δｘ，ｙ１的对应增量Δｙ不变；而ｙ２＝sinｘ是正弦曲线，在［0，π］上是上凸的，在［π，2π］上是下凸的，故每当ｘ增加一个单位增量Δｘ时，ｙ２对应的增量ｉ（ｉ=1，2，3，…）在［0，π］上越来越小，在［π，2π］上是越来越大，故当ｘ增加一个单位增量Δｘ时，对应的f(x)的变化，在ｘ∈［0，π］上其增量Δf(x)ｉ（ｉ＝1，2，3，…）越来越大，在ｘ∈［π，2π］上，其增量Δf(x)ｉ则越来越小，故f(x)关于ｘ的函数图象，开始时在［0，π］上是下凸的，后来在［π，2π］上是上凸的，故选D．◇题目：（07 江西）四位好朋友在一次聚会上，他们按照各自的爱好选择了形状不同、内空高度相等、杯口半径相等的圆口酒杯，如图所示．盛满酒后他们约定：先各自饮杯中酒的一半．设剩余酒的高度从左到右依次为h1，h2，h3，h4，则它们的大小关系正确的是（）A．h2＞h1＞h4B．h1＞h2＞h3C．h3＞h2＞h4D．h2＞h4＞h1解：设内空高度为H, 剩余酒的高度关于酒杯中酒的体积函数从左到右依次为V1（h）、V2（h）、V3(h)、V4（h），根据酒杯的形状可知函数V1（h）、V2（h）、V4（h）的图象可为上右图.因为函数V 1（h ）、V 2（h ）为下凸函数, V 1（h ）当h 从Ｏ→H ，Δh 增加一个单位增量， ΔV ｉ（ｉ＝1，2，3，…）增大，则h 1> 0.5H =h 4；同理V 2（h ）当h 从Ｏ→H ，Δh 增加一个单位增量，ΔV ｉ（ｉ＝1，2，3，…）增大，则h 2> 0.5H =h 4；所以h 1> h 4、 h 2> h 4；由V 1（h ）、V 2（h ）图象可知，h 从H →h 2，ΔV 1（h ）>ΔV 2（h ）,而0.5 V 1（h ）>ΔV 1（h ）,ΔV 2（h ）=0.5 V 2（h ）,则当ΔV 1（h ）=0.5 V 1（h ）时h 1> h 2，所以答案为A.题型2：函数与图像问题◇题目： 在x y x y x y y x2cos ,,log ,222====这四个函数中,当210x x <<时，2)()()2(2121x f x f x x f +>+ 恒成立的函数的个数是( ). A.0 B.1 C.2 D.3【分析】：运用数形结合思想,考察各函数的图象.注意到对任意x 1,x 2∈I,且x 1<x 2,当f(x)总满足2)()()2(2121x f x f x x f +>+时,函数f(x)在区间I 上的图象是“上凸”的,由此否定y=2x ,y=x 2,y=cos2x ，应选B 。

函 数 练 习 题班级 姓名一、 求函数的定义域1、求下列函数的定义域：⑴y =⑵y =⑶01(21)111y x x =+-++-2、设函数f x ()的定义域为[]01，，则函数f x ()2的定义域为_ _ _；函数f x ()-2的定义域为________；3、若函数(1)f x +的定义域为[]-23，，则函数(21)f x -的定义域是 ；函数1(2)f x+的定义域为 。

4、 知函数f x ()的定义域为 [1,1]-，且函数()()()F x f x m f x m =+--的定义域存在，求实数m 的取值范围。

二、求函数的值域5、求下列函数的值域：⑴223y x x =+- ()x R ∈ ⑵223y x x =+- [1,2]x ∈ ⑶311x y x -=+ ⑷311x y x -=+ (5)x ≥⑸y = ⑹ 225941x x y x +=-＋ ⑺31y x x =-++ ⑻2y x x =-⑼y ⑽4y =⑾y x =-6、已知函数222()1x ax bf x x ++=+的值域为[1，3]，求,a b 的值。

三、求函数的解析式1、 已知函数2(1)4f x x x -=-，求函数()f x ，(21)f x +的解析式。

2、 已知()f x 是二次函数，且2(1)(1)24f x f x x x ++-=-，求()f x 的解析式。

3、已知函数()f x 满足2()()34f x f x x +-=+，则()f x = 。

4、设()f x 是R 上的奇函数，且当[0,)x ∈+∞时， ()(1f x x =+，则当(,0)x ∈-∞时()f x =____ _()f x 在R 上的解析式为5、设()f x 与()g x 的定义域是{|,1}x x R x ∈≠±且，()f x 是偶函数，()g x 是奇函数，且1()()1f xg x x +=-，求()f x 与()g x 的解析表达式四、求函数的单调区间6、求下列函数的单调区间：⑴ 223y x x =++ ⑵y = ⑶ 261y x x =--7、函数()f x 在[0,)+∞上是单调递减函数，则2(1)f x -的单调递增区间是8、函数236xy x -=+的递减区间是 ；函数y =的递减区间是五、综合题9、判断下列各组中的两个函数是同一函数的为 （ ） ⑴3)5)(3(1+-+=x x x y ， 52-=x y ； ⑵111-+=x x y ， )1)(1(2-+=x x y ；⑶x x f =)(， 2)(x x g = ； ⑷x x f =)(，()g x =； ⑸21)52()(-=x x f ， 52)(2-=x x f 。

高一经典函数练习题及完美解析函数练习1 函数（一）1．下列各组函数中，表示相同函数的是 （ ）A f(x)=x 与 g(x)=xx 2B f(x)=|x| 与 g(x)=2xC f(x)=12-x 与g(x)=1-x • 1+xD f(x)=x 0与g(x)=1 1． 函数y=x--113的定义域为 （ ）A （－∞，1]B (-∞，0) (0,1]C (-∞，0) (0,1)D [1,+ ∞)2． 下列函数中值域是R ＋的是 （ ）A y=2x+1 (x>0)B y=x 2C y=112-x D y=x2 3． 函数y=22++-x x 的定义域为__________,值域为_____________.4． 已知f(x)=x 2+1,则f[f(-1)]=______________________ 5． 求下列函数的定义域；（1）y=x111+； （2）y=xx x -+||)1(07．用可围成32m 墙的砖头，沿一面旧墙围猪舍四间（其平面图为連成一排大小相同的四个长方形，如图），应怎样围，才能使猪舍的总面积最大？最大面积是多少？函数练习2 函数（二）1． 下面四个函数：（1）y=1-x (2) y=2x-1 (3) y=x 2-1 (4) y=x5，其中定义域与值域相同的函数有 （ ）A 1个B 2个C 3个D 4个2． 下列图象能作为函数图象的是 （ ）A B C D 3． （1）数集｛x|4≤x<16｝用区间表示为_________；（2）数集｛x||x|≤3｝用区间表示为_______；（3）数集｛x|x ∈R ，且x ≠0｝用区间表示为_______；4． 已知f(x)=⎪⎩⎪⎨⎧--3210x )0()0()0(<=>x x x ，求f{f[f(5)]}的值。

5． 已知f(x)的定义域为（0,1）求f(x 2)的定义域 6．若2f(x)+f(-x)=3x+1，求f(x)的解析式。

函数的最值问题（高一）一．填空题：1. f ( x)3x 5, x[3,6] 的最大值是。

f ( x)11,3 的最小值是。

， xx2.函数 y 12 4x x 2 的最小值是，最大值是 3.函数 y1的最大值是，此时 x2 x 2 8x104.函数 y 2x 3 3, 2 的最小值是，最大值是x , x15.函数 y 3 2, 1 的最小值是，最大值是x , xx 16.函数 y= x 2 - 的最小值是。

y x 1 2x 的最大值是x 27.函数 y=|x+1| –|2-x| 的最大值是 最小值是.8.函数 f x2 在 [2,6] 上的最大值是 最小值是。

x 19.函数 y= 3x（ x ≥ 0）的值域是 ______________.1 2x10.二次函数 y=-x 2+4x 的最大值11. 函数 y=2x 2-3x+5 在[-2 ，2] 上的最大值和最小值 。

12.函数 y= -x 2 -4x+1 在 [-1 , 3] 上的最大值和最小值13.函数 f （ x ） =1 的最大值是y 2x 22x 5的最大值是1 x(1 x)x 2 x 114. 已知 f （ x ） =x 2－ 6x+8， x ∈［ 1，a ］并且 f （ x ）的最小值为 f （ a ），则 a 的取值范围是15.函数 y= –x 2–2ax(0 x 1)的最大值是 a 2,那么实数 a 的取值范围是16．已知 f （ x ）=x 2－2x+3 ，在闭区间［ 0， m ］上有最大值 3，最小值 2，则 m 的取值范围是17. 若 f(x)= x2+ax+3 在区间 [1,4] 有最大值 10，则 a 的值为：18.若函数 y=x 2 3x 4 的定义域为 [0,m], 值域为 [ 25/4, 4],则 m 的取值范围是19. 已知 f （ x ） =-x 2+2x+3 , x ∈［ 0， 4］ ,若 f （ x ）m 恒成立， m 范围是。

三角函数的诱导公式(一)【知识梳理】1. 诱导公式⑴角n+ a与角a的终边关于原点对称. 如图所示.10丿H(2)公式：sin( n+ a = —sin acos( n+ a) =—cos_ a.tan( n+ a = tan_ a2. 诱导公式三(1)角一a与角a的终边关于X轴对称. 如图所示.彳(2)公式：sin( —a = —sin _aCOs(— a) = COs_ atan(— a = —tan_ a3. 诱导公式四(1)角n— a与角a的终边关于y轴对称.如图所示.(2)公式：sin( n— a = sin __ acos( n— a = 一COS_a tan( n— a = —tan_ a.【常考题型】题型一、给角求值问题【例1】 求下列三角函数值:。

o 119 n⑴sin( — 1 200 °; (2)tan 945 ; (3)cos_^.［解］(1)si n( — 1 200 )=— sin 1 200 =—°si n(3 x 360 牛 120 ) =— sin 120 =— sin(180 — 60 )3=—sin 60 =——; 2(2)tan 945 =tan(2 x 360 °+ 225 °= tan 225 = tan( 180 4 45 °)= tan 45 = 1;【类题通法】【对点训练】求 sin 585 cos 1 290 4 cos( — 30°)sin 210 4 tan 135 的值.解：sin 585 °s 1 290 C cos(— 30°)sin 210 ° tan 135 = sin(360 ° 225°)cos(3x 360° 4 210) 4 cos 30 gin 210 半 tan(180 —45 ° = sin 225 c6s 210 半 cos 30 s °n 210 — tan 45 = sin( 180 半 45 °)cos(180 4 30 °)4 cos 30 sin(180 4 30 °— tan 45 =sin 45 cbs 30 — cos 30 s i n 30 — tan 45 = 返 x ©_ ?/3x 1—1 乎-也-42 2 2 2 4题型二、化简求值问题cos — a tan 7 n4 asin n — a(2)化简曲:豊4 " * "—1需°cos — 180 — a sin — a — 180 (3)cos 譽 =cos 20 n — n = cos 6 6n =cos ：= 6 【例2】 (1)化简:cos — a tan 7 n4 a 解析］sin n— a cos d an n4 asin acos a tan asin a心=1sin a［答案］1•••a+ 125°= 180°+ ( a — 55°),sin 4X 360 °+ a c os 3 x 360 °— a sin a c os — a (2)［解］原式=—— cos 180 + a ［ — sin 180 + a ］ COS a = =—1. —cos a sin a — COs a 【类题通法】 利用诱导公式一〜四化简应注意的问题(1)利用诱导公式主要是进行角的转化，从而达到统一角的目的;(2)化简时函数名没有改变，但一定要注意函数的符号有没有改变;(3)同时有切(正切)与弦(正弦、余弦)的式子化简，一般采用切化弦，有时也将弦化切. 化简： tan 2 n — 0 sin 2 n — 0 cos 6 n —tan — 0s in — 0cos — 0—cos 0sin n+ 0 tan Osin 0cos 0cos 0sin 0 =tan 0 题型三、给角(或式)求值冋题【例3】 1 (1)已知 sin 3= 3, cos(a+ 3=— 1,贝U sin( a+ 2 3)的值为( ) 3 A . 1 B . — 11 Ci 1D 「11⑵已知cos( a — 55 °)=— 3，且a 为第四象限角，求 sin( a+ 125°)的值.(1)［解析］ **cos( a+ 3) = — 1 ,• '•a+ 3= T H- 2k n, k , 1 •'sin( a+ 2 3) = sin ［(a+ 3］ = sin( n+ 3 = — sin 3= — 3.3［答案］D(2)［解］・.cos( a — 55 °)=— ］0,且a 是第四象限角.• a — 55°是第三象限角.sin( a — 55 °)= — i ： 1 — COS ? a — 55 =— 2.23【对点训练】解：原式=••sin( a- 125° = sin[180 — (a — 55°)] = — sin( a — 55°)=警.【类题通法】解决条件求值问题的策略(1)解决条件求值问题，首先要仔细观察条件与所求式之间的角、函数名称及有关运算之间 的差异及联系.(2)可以将已知式进行变形向所求式转化，或将所求式进行变形向已知式转化.【对点训练】1 、sin( n+ a=— 3,求 cos(5n+ a 的值. 3由诱导公式得，sin( n- a = — sin a,当a 是第一象限角时，cos a= - ；1 — Sin 2 a=彳^2 2A /2 此时，cos(5 n — %)= cos( n+ a = —cos a=— 3 . 3当 a 是第二象限角时，cos a=— • ：1— sin 2 a=— ^^2 ,2占 此时，cos(5 n — %)= cos( n+ a = — cos a= 3 .3 【练习反馈】1.如图所示，角0的终边与单位圆交于点 P ，晋，则cos(n — 的值为(B . — -5 52*5D. 50-五—5，送•'cos( n — ® = — cos 0= 5 .已知 解: 所以sin a= 3，所以a 是第一象限或第二象限角.解析: 选 C 行=1 ,「.cos答案：2 — 2n5.已知 cos 6"coS a+于的值.n —cos 6— a 2. 4 _ 已知 sin( n+%)= 5，且 a 是第四象限角，贝U COS （ a — 2冗）的值是（ ） 3 B.5D.5 4 解析：选 B sin a =-4, 又a 是第四象限角, • 'COS ( a — 2 n )= COS a= \ -1- Sin 2 a= 5. sin a — 3 n + COS n — a 3.设 tan(5 n+ a) = m ,贝U sin — a — COS n+ a 解析： '•ta n(5n+ a = tan a= m , —sin a — cos a — tan a — 1 — m — 1 m + 1 • • •原式= = = = —sin a+ cos a — tan a+ 1 — m + 1 m — 1 答案:cos — 585 ° sin 495 + sin — 570的值是解析: 原式= cos 360 °+ 225 ° sin 360 °+ 135 ° — sin 210 °+ 360 cos 225 cos 180 °+ 45 ° sin 135 — sin 210 °sin 180 °— 45° — sin 180 ° + 30° —cos 45sin 45 + sin 30 —2 .2 1 + _ 2 2 2 — 2.解：cos n+ =— cos n —6 5 n a+E。

集合根底训练A组一、选择题:1．以下各项中，不可以组成集合的是〔C〕A．所有的正数B．等于2的数C．接近于0的数D．不等于0的偶数2．以下四个集合中，是空集的是〔D〕A．{x|x33}B．{(x,y)|y2x2,x,yR}C．{x|x20}D．{x|x2x10,xR}3．以下表示图形中的阴影局部的是〔A〕A．(AUC)I(BUC)A B B．(AUB)I(AUC)C．(AUB)I(BUC)D．(AUB)I C C 4．下面有四个命题：〔1〕集合N中最小的数是1；〔2〕假设a不属于N，那么a属于N；〔3〕假设a N,b N,那么ab的最小值为2；〔4〕x212x的解可表示为1,1其中正确命题的个数为〔A〕A．0个B．1个C．2个D．3个5．假设集合M a,b,c中的元素是△ABC的三边长，那么△ABC一定不是〔D〕A．锐角三角形B．直角三角形C．钝角三角形D．等腰三角形二、填空题:1．假设集合2．设集合A x|3 x 7，B x|2 x 10，那么AUBx|2 x10 A {x 3 x 2},B {x2k 1 x 2k 1},且A B，那么实数k的取值范围是k|1k 1 23．Ayy x22x1,B yy2x1，那么AI B y|y0三、解答题:1．集合A8N，试用列举法表示集合A xN|6x解：由题意可知6x是8的正约数，当6x1,x5；当6x2,x4；当6x4,x2；当6x8,x2；而x0，∴x2,4,5，即A2,4,512A{x2x5}， B{xm1x2m1}，BA ,m 的取值范围．求 解：当m 1 2m1，即m 2时，B ,满足BA ，即m 2；当m12m1，即m2时，B3,满足BA ，即m2；当m12m 1，即m2时，由Bm 1 2即2m 3；A ，得1 52mm33A a,a1, 3,Ba 3,2a 1,a 1 ，假设AI B3，求实数a 的值．集合22解：∵AI B3 ，∴ 3 B ，而a 2 1 3，∴当a3 3,a 0,A0,1, 3,B3,1,1，这与AI B3 矛盾；当2a 1 3,a 1,符合AI B3∴a14．设全集，2有实数根，2有实数根,求CMINUR Mm|mxx10Nn|xxn0 U解：当m0时，x1，即0 M ；当m 0时， 14m0,即m 1 0，且m4∴m1 ，∴C U Mm|m1 , 而对于N ， 14n0,即n1 ，∴Nn|n14444∴(C U M)I Nx|x14综合训练B 组一、选择题1．以下命题正确的有〔A 〕〔1〕很小的实数可以构成集合；〔2〕集合 y|yx 2 1与集合 x,y|yx 2 1是同一个集合；3 61 5个元素；〔3〕1,,,这些数组成的集合有2 42〔4〕集合 x,y|xy0,x,yR 是指第二和第四象限内的点集。

（word完整版）⾼中三⾓函数最值问题难题⾼中三⾓函数最值问题难题⼀、直接应⽤三⾓函数的定义及三⾓函数值的符号规律解题例1：求函数y ＝xx x x x x x x cot |cot ||tan |tan cos |cos ||sin |sin +++的最值分析：解决本题时要注意三⾓函数值的符号规律，分四个象限讨论。

解：（1）当x 在第⼀象限时，有sin cos tan cot 4sin cos tan cot x x x xy x x x x =+++=（2）当x 在第⼆象限时，有sin cos tan cot 2sin cos tan cot x x x xy x x x x =+++=----（3）当x 在第三象限时，有sin cos tan cot 0sin cos tan cot x x x xy x x x x =+++=--（4）当x 在第四象限时，sin cos tan cot 2sin cos tan cot x x x xy x x x x=+++=----综上可得此函数的最⼤值为4，最⼩值为-2. ⼆、直接应⽤三⾓函数的有界性（sin 1,cos 1x x ≤≤）解题例1：（2003北京春季⾼考试题）设M 和m 分别表⽰函数cos 13x -1y=的最⼤值和最⼩值，则M m +等于（）（A ）32（B ）32-（C ） 34-（D ）-2解析：由于cos y x =的最⼤值与最⼩值分别为1,-1,所以,函数cos 13x -1y=的最⼤值与最⼩值分别为32-,34-,即M m +＝32-+（34-）=-2,选D.例2：求3sin 1sin 2x y x +=+的最值（值域）分析：此式是关于sin x 的函数式，通过对式⼦变形使出现12sin 3yx y -=-的形式，再根据sin 1x ≤来求解。

解：3sin 1sin 2x y x +=+，即有sin 23sin 1sin 3sin 12y x y x y x x y +=+?-=-12(3)sin 12sin 3yy x y x y --=-?=-。

函数压轴题 一、函数的性质1.已知函数)1()(xx e e x x f -=，若f （x 1)<f （x 2），则（ ） A ．x 1>x 2 B ．x 1＋x 2＝0 C ．x 1<x 2 D ．2221x x <2。

f (x )是定义在（0,＋∞）上的单调增函数，满足f (xy ）＝f (x ）＋f （y ），f （3）＝1，若f (x ）＋f （x －8)≤2，则x 的取值范围为________．3。

要使函数22)(-+=x kx x f 与y ＝log 3(x －2)在(3,＋∞)上具有相同的单调性，则实数k 的取值范围是________．4.已知函数f (x )是（－∞，＋∞）上的奇函数，且f （x ）的图象关于x ＝1对称，当x ∈［0，1］时，f （x )＝2x －1，①求证：f （x ）是周期函数；②当x ∈［1，2］时，求f （x )的解析式;③计算f (0）＋f （1)＋f （2）＋…＋f （2 017）的值．5.已知f （x )是定义在R 上的偶函数，g （x )是定义在R 上的奇函数，且g (x )＝f (x －1),则f (2 013）＋f (2 015)的值为( )A ．－1B ．1C ．0D ．无法计算6.设f (x )是定义在R 上的奇函数，且对任意实数x ，恒有f （x ＋2）＝－f (x ）．当x ∈［0,2]时,f (x )＝2x －x 2.(1)求证：f （x ）是周期函数；（2)当x ∈[2，4]时，求f （x ）的解析式； (3）计算f （0）＋f （1)＋f （2)＋…＋f (2 014)．7.奇函数f （x ）的定义域为R ，若f （x ＋2)为偶函数，且f （1）＝1，则f （8）＋f （9)＝( ）A ．－2B ．－1C ．0D ．18。

若函数)1ln()(2++=x x x x f 为偶函数，则a ＝________． 9.若函数))(12()(a x x xx f -+=为奇函数,则a ＝________10.已知f (x )是定义在R 上的奇函数，当x ≥0时,f (x )＝3x ＋m （m 为常数），则f (－log 35）的值为( )A ．4B ．－4C ．6D ．－611.已知函数f (x ）是定义在R 上的偶函数，且在区间［0，＋∞)上单调递增．若实数a 满足)1(2)(log )(log 212f a f a f ≤+,则a 的取值范围是( ）A ．［1，2］B 。

一、选择题（共6小题）1、在函数中，自变量x的取值范围是（）A、x≠0B、x≤﹣2C、x≥﹣3且x≠0D、x≤2且x≠02、函数的定义域是（）A、x≠2B、x≥﹣2C、x≠﹣2D、x≠03、（2006•黄石）函数y=的自变量x的取值范围是（）A、x≥﹣2B、x≥﹣2且x≠﹣1C、x≠﹣1D、x＞﹣14、（2010•苏州）在函数y=中，自变量x取值范围是（）A、x＞1B、x＜﹣1C、x≠﹣1D、x≠15、（2008•乐山）函数的自变量x的取值范围为（）A、x≥﹣2B、x＞﹣2且x≠2C、x≥0且≠2D、x≥﹣2且x≠26、能使有意义的x的取值范围是（）A、x＞﹣2B、x≥﹣2C、x＞0D、x≥﹣2且x≠0二、填空题（共6小题）7、（2011•黑龙江）函数y=中，自变量x的取值范围是_________．8、（2007•黄石）函数的自变量取值范围是_________．9、求使代数式有意义的x的整数值_________．10、函数y=+（x﹣1）0自变量的取值范围是_________．11、函数y=中，自变量x的取值范围是_________．12、写出一个y关于x的函数关系式，使自变量x的取值范围是x≥2且x≠3，则这个函数关系式可以是_________．答案与评分标准一、选择题（共6小题）1、在函数中，自变量x的取值范围是（）A、x≠0B、x≤﹣2C、x≥﹣3且x≠0D、x≤2且x≠0考点：函数自变量的取值范围。

专题：常规题型。

分析：根据被开方数x+3大于等于0，分母x不等于0，列式求解即可．解答：解：根据题意得，，解得x≥﹣3，且x≠0．故选C．点评：本题主要考查了函数自变量的取值范围，被开方数大于等于0，分母不等于0列式求解即可，是基础题，比较简单．2、函数的定义域是（）A、x≠2B、x≥﹣2C、x≠﹣2D、x≠0考点：函数自变量的取值范围；二次根式有意义的条件。

专题：计算题。

分析：本题主要考查自变量的取值范围，函数关系中主要有二次根式．根据二次根式的意义，被开方数是非负数．解答：解：根据题意得：x+2≥0，解得x≥﹣2．故选B．点评：函数自变量的范围一般从三个方面考虑：（1）当函数表达式是整式时，自变量可取全体实数；（2）当函数表达式是分式时，考虑分式的分母不能为0；（3）当函数表达式是二次根式时，被开方数为非负数．3、（2006•黄石）函数y=的自变量x的取值范围是（）A、x≥﹣2B、x≥﹣2且x≠﹣1C、x≠﹣1D、x＞﹣1考点：函数自变量的取值范围；分式有意义的条件；二次根式有意义的条件。

求证:恰有一个定义在所有非零实数上的函数f,满足:⑴对任意x MQ f(x)=x*f(1/x);(2)对所有的x=y 且xy 工0,有f(x)+f(y)=1+f(x+y)解：首先，令g(x)=f(x)-1 ，把条件写成g(x+y)=g(x)+g(y) ……⑴g(x)+1=xg(1/x)+x (2)(1)称为Cauchy 函数方程，一般来讲是需要额外条件(诸如连续性、单调性之类)才能得到g是线性函数，对于这个问题而言，(2)就是所谓的额外条件，所以不再需要连续性的条件。

首先，在(2)当中取x=-1 得到g(-1)=-1 。

再对(1)取y=-x-1 得-1=g(x-x-1)=g(x)+g(-x)+g(-1)，所以g(-x)=-g(x)，即g 是奇函数。

将(2)变形为g(x)-x=x[g(1/x)- 1/x] (3)如果存在a>0使得g(a)>a，那么g(1/a)>1/a，禾U用奇函数的性质，g(-a)=-g(a)<-a，继续在(3) 中取x=-a 得到g(-1/a)>-1/a ，这样g(1/a)=-g(-1/a)<1/a ，矛盾。

同理可以证明不存在a>0 使得g(a)<a，所以a>0时只能有g(a)=a。

再利用奇函数的性质得a<0时也有g(a)=a，即⑴和(2) 只有唯一解g(x)=x 。

已知定义在R上的函数f(x)对任意实数x, y都满足f(x+y)=f(x)+f(y)，且当x > 0时，f(x) > 0。

求：(1 )求f(0)；(2)判断函数f(x)的奇偶性，并证明；(3 )解不等式f(a-4)+f(2a+1) v 0。

解：(1)函数f (x)为R上的奇函数，下面证明：令y=x=0，由 f (x+y) =f (x) +f (y),得 f (0) =f (0) +f (0),所以 f (0) =0,令y=-x，由 f (x+y ) =f (x) +f (y)，得 f (0) =f (x) +f (-x),即0=f (x) +f (-x), 所以f(-x) =-f(x)，又f (x)定义域为R，关于原点对称，所以f (x)为奇函数；(2)任取x1, x2，且x1 v x2 ,则 f (x2) -f (x1 ) =f[ (x2-x1 ) +x1]-f (x1) =f (x2-x1) +f (x1) -f (x1) =f (x2-x1 ),因为x> 0 时，f( x)> 0，且x2-x1 > 0，所以f(x2-x1 )> 0，即f(x2) -f(x1)> 0，f(x2)> f(x1)，所以f (x)为R上的增函数，f(a-4) +f(2a+1)v 0? f(2a+1)v -f(a-4) =f(4-a)，由f (x)为增函数得，2a+1 v 4-a，解得a v 1.所以不等式的解集为{a|a v 1}．已知函数f ( x)是定义在R上的偶函数，且对任意的x€ R,都有f (x+2 ) =f (x).当0W x<1 时，f (x) =x2 .若直线y=x+a与函数y=f (x)的图象在[0, 2]内恰有两个不同的公共点，则实数 a 的值是( )解：由已知条件f(x)为R上的偶函数，且满足f(x+2)=f(x)，当0<x<时，f(x)=x2有：f(x) 为最小正周期为T=2 的周期函数f(x) 的图像草图如下直线y=x+a 表示的是斜率k=1 的一组平行直线当x€ ［0,2］时，显然在a=0时【如直线L1】直线与f(x)恰有两个交点(0,0)和(1,1) 当直线y=x+a与y= x2在［0,2］内相切时，联立得到：x2=x+a ===> x2-x-a=0由^ =b2-4ac=1+4a=0 有a=-1/4此时切点坐标为(1/2,1/4)在［0,2］内那么，直线L2与f(x)在［0,1］和［1,2］上分别有一个交点当a€ (-1/4,0)时【即直线位于L1、L2之间时】，它们就有3个交点当a€ ［-2,-1/4)时，它们就只有1个交点综上，满足条件的a的值有两个：a=-1/4，或者a=0.设f(x)是定义在R上的奇函数，且当x> 0时，f(x)=2 x-3，贝U f(-2)的值等于解：I f(x)是定义在R上的奇函数••• f(-2)= -f(2)=-(2 2-3)= -1.定义在区间(0, +R)上的函数f (x)满足：(1) f (x)不恒为零；(2)对任意a€ R+, b € R，都有f (ab) =bf (a).(I)求f (1)的值；(n)求证方程f (x) =0有且只有一个实数根；(川)若f (2)> 0,试证f (x )是(0, +8)上的增函数.(I)依题意，令a=1 , b=2，即可求得f (1)的值；4)由(1)知，存在x0 €( 0, +8),使得f( x0)工0 任取x1 €( 0, +8)且x1^1, 结合题意即可证得方程 f ( x) =0有且只有一个实数根；(川)对任意的0v x1 v x2 v +8,存在实数p1, p2，使得x1=2p1 , x2=2p2，且p1 v p2 , 作差判断即可证得结论.解答：(I)解：••• f (ab) =bf (a),令a=1, b=2 ,• f (1) =f (12) =2f (1),• f (1) =0. (3 分)(n)证明：由(1)知，存在x0 €( 0 , +8),使得f(x0) M0显然X0M1.任取x1 €( 0, +8)且x1^1,贝V必存在实数q,使得x1=x0q , q M0由(2)知 f ( x1) =f (x0q ) =qf ( x0) MQ故f (x) =0有且只有一个实数根x=1 . (8分)(川)证明：对任意的0v x1 v x2 v +8,存在实数 pl , p2，使得 x1=2p1 , x2=2p2，且 pl v p2,f (xl ) -f (x2) =f (2p1) -f ( 2p2) =p1f (2) -p2f (2)=(p1-p2 ) f (2)v 0, ••• f (xl )v f ( x2), •••函数f (乂)在(0, +s)上单调递增.(14分)点评：本题考查抽象函数及其应用，着重考查函数单调性的判断与证明，属于中档题. (1 )设f (x )是定义在 R 上奇函数，且当 x > 0时，f (x ) =2x-3，则当x v 0时，求f ( x ) 表达)x+3 (2)设 f (x )是定义在 R 上奇函数，且 f (x+1) =-f (x ),当 x € (0, 1)时，f ( x ) =2x-3 , 则x €( 3, 4)时，求f (x )表达式 解：(1 )设 x v 0,则-x >0 , • f (-x ) =2-x -3 ,•/ f (x )为定义在R 上的奇函数 1二 f (x ) =-f (-x ) =-2-x +3=-(2) 1 •••当 x v 0 时，f (x )二-^广 3; (2)因为 x €( 0, 1)时，f (x ) =2x -3, 设 x €( -1 , 0)时，-x €( 0, 1), • f (-x ) =2-x -3 ,••• f (x )为定义在 • f (x ) =-f (-x ) •••当 x €( -1 , 0)R 上的奇函数=-2-x -3=-(j )x1 x f ( x ) =-(2)x-4 €( -1 , 0) 时, 所以x €( 3, 4)时，1 • f (x-4 ) = (')4 x2 ••• f (x+1 ) =-f ( x ), • f (x+2 ) =-f (x+1 ) =f (x ), • f (x )是以2为周期的周期函数, 1 4 xf (x-4) =f (x ) = ( ) 3 ； 2 1 • x €( 3 , 4)时，f (x ) = (一)4 x。

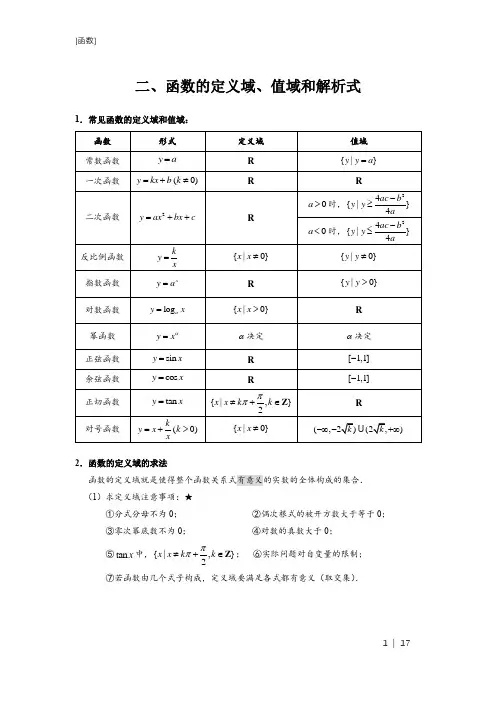
二、函数的定义域、值域和解析式1．常见函数的定义域和值域：2．函数的定义域的求法函数的定义域就是使得整个函数关系式有意义的实数的全体构成的集合． （1）求定义域注意事项：★①分式分母不为0； ②偶次根式的被开方数大于等于0；③零次幂底数不为0； ④对数的真数大于0； ⑤tan x 中，{|,}2x x k k ππ≠+∈Z ； ⑥实际问题对自变量的限制；⑦若函数由几个式子构成，定义域要满足各式都有意义（取交集）．（2）抽象函数的定义域：①定义域是x的取值范围★②括号内范围等同★3．函数值域的求法对于函数(),y f x x A =∈，与x 的值相对应的y 值叫做函数值．函数值的集合{()|}f x x A ∈叫函数的值域．（1）观察法：从自变量x 的范围出发，推出()y f x =的取值范围．（2）二次函数在区间上的值域：画出简图，找到对称轴和对应取值区间来求值域．（3）换元法：通过对函数解析式进行适当换元，通常把无理函数转化为有理函数，换元后应先确定新元的取值范围．（4）分离常数法：将形如ax by cx d+=+的有理分式转化为“反比例函数”的形式a k y c cx d =++，确定函数值域为{|}ay y c≠．（5）判别式法：把函数转化为关于x 的二次方程，通过方程有实根，判别式0∆≥，从而求得原函数的值域．（6）单调性法：确定函数在定义域（或某个定义域的子集）上的单调性，求出函数的值域．4．求函数解析式（1）配凑法：已知某区间上的解析式，求其他区间上的解析式，将待求变量转化到已知区间上，利用函数满足等量关系间接获得其解析式．（2）换元法：已知(())()f h x g x =求()f x 时，往往可设()h x t =，从中解出x ，带入()g x 进行换元，求出()f t 的解析式，再将t 替换为x 即可，注意新元t 的取值范围．（3）待定系数法：若已知函数类型（如一次函数、二次函数等），根据函数类型设出函数解析式，根据题设条件，列出方程组，解出待定系数即可．（4）解方程组法：已知关于()f x 与1()f x（或()f x -）的表达式，可根据已知条件再构造出另一个方程，构成方程组求出()f x ．练习题：答案解析：答案：153()888xf xx=+-29解析：()2()31f x f x x--=-…………①用x-替换x得()2()31f x f x x--=--……②两式联立解得()1f x x=+．答案：A数学浪子整理制作，侵权必究。

高一数学同步训练:1.3 三角函数的诱导公式一. 选择题A． 1. 下列各式不正确的是（）sin（α＋180°）=－sinα B. cos（－α＋β）=－cos（α－β）C. sin（－α－360°）=－sinαD. cos（－α－β）=cos（α＋β）2. 的值为（）A. B. C. D.3. 的值等于（）A. B. C. D.4. sin585°的值为()A. －B.C. －D.5. sin(－π)的值是()A. B. － C. D. －6. cos(－225°)＋sin(－225°)等于()A. B. － C. 0 D.7. cos2010°＝()A. －B. －C.D.8. 已知sin(α－)＝, 则cos( ＋α)的值为()A. B. － C. D. －9. 若则的值是（）A. B. C. D.10. 已知cos( ＋α)＝－, 且α是第四象限角, 则cos(－3π＋α)()A.B. －C. ±D.11. sin ·cos ·tan 的值是（）A. －B.C. －D.12. 若, 则的值为（）A. ；B. ；C. ；D.13. 已知cos( ＋φ)＝, 且|φ|< , 则tanφ＝()A. －B.C. －D.14. 设tan(5π＋α)＝m, 则的值等于()A. B. C. －1 D. 115. A.B.C 为△ABC 的三个内角, 下列关系式中不成立的是( )①cos(A ＋B )＝cos C ②cos B ＋C 2＝sin A2③tan(A ＋B )＝－tan C ④sin(2A ＋B ＋C )＝sin A A. ①② B. ③④ C. ①④ D. ②③ 16. 已知 , 则 值为（ ） A....B.—.. C.... D.—17. cos ( +α)= — , <α< ,sin( -α) 值为（ ） A... B... C....D.—18. tan110°＝k, 则sin70°的值为( ) A A. － B. C. D. －19. 化简: 得（ ）A....B...C....D.±20．已知 , , 那么 的值是（ ） A 231+- B 231+- C 231- D 231+21. (2011年潍坊高一检测)已知a ＝tan(－ ), b ＝cos π, c ＝sin(－ π), 则a 、b 、c 的大小关系是( )A. b>a>cB. a>b>cC. b>c>aD. a>c>b22. （2009.济南高一检测）若 , 则 等于（ ） A. B. C. D.23.（2009·福州高一检测）已知f(cosx)=cos3x,则f(sin30°)的值等于（ ） （A ）-1 （B ）1 （C ）12（D ）0 二. 填空题1.tan2010°的值为 . 2．sin （- ）....3. tan －cos(－ )＋sin(－ )的值为________.4. cos( -x)= , x ∈（- , ）, 则x 的值为 .5. 化简 ＝________.cos20°－sin20°6. 若P(－4,3)是角α终边上一点, 则 的值为________.7. 式子cos2 ＋cos2 ＝________. 18. 若tan(π－α)＝2, 则2sin(3π＋α)·cos ＋sin ·sin(π－α)的值为________.9. 化简: ＝______ ___. 10．已知 , 则 = ．11. 若 , 则 ＝ ____ ____.12. 如果 且 那么 的终边在第 象限13. 求值: 2sin(－1110º) －sin960º+ ＝ .14. 已知cos( ＋θ)＝ , 则cos( －θ)＝________.15.已知(),41cos -=-απ则=⎪⎭⎫⎝⎛+απ23sin16, 已知 , 则 的值是1、 三. 解答题求cos （－2640°）+sin1665°的值.2. 化简（1）（2）0sin(180)cos()tan()ααα+--3. 化简4. 已知f(α)＝ .(1)化简f(α)；(2)若α是第三象限角, 且cos(α－ )＝ , 求f(α)的值．5. 设 , 求 的值.6. 已知方程sin(( ( 3() = 2cos(( ( 4(), 求 的值。

函数的单调性一、选择题：1．在区间(0，＋∞)上不是增函数的函数是（ ）A ．y =2x ＋1B ．y =3x 2＋1C ．y =x2D ．y =2x 2＋x ＋12．函数f (x )=4x 2－mx ＋5在区间［－2，＋∞］上是增函数，在区间(－∞，－2)上是减函数，则f (1)等于 （ ） A ．－7 B ．1 C ．17 D ．253．函数f (x )在区间(－2，3)上是增函数，则y =f (x ＋5)的递增区间是 （ ） A ．(3，8) B ．(－7，－2) C ．(－2，3) D ．(0，5) 4．函数f (x )=21++x ax 在区间(－2，＋∞)上单调递增，则实数a 的取值范围是 （ ）A ．(0，21)B ．( 21，＋∞)C ．(－2，＋∞)D ．(－∞，－1)∪(1，＋∞)5．已知函数f (x )在区间[a ，b ]上单调，且f (a )f (b )＜0，则方程f (x )=0在区间[a ，b ]内（ ） A ．至少有一实根 B ．至多有一实根 C ．没有实根 D ．必有唯一的实根 6．已知函数f (x )=8＋2x －x 2，如果g (x )=f ( 2－x 2 )，那么函数g (x ) （ ） A ．在区间(－1，0)上是减函数 B ．在区间(0，1)上是减函数 C ．在区间(－2，0)上是增函数 D ．在区间(0，2)上是增函数7．已知函数f (x )是R 上的增函数，A(0，－1)、B(3，1)是其图象上的两点，那么不等式|f (x ＋1)|＜1的解集的补集是 （ ） A ．(－1，2) B ．(1，4)C ．(－∞，－1)∪[4，＋∞）D ．(－∞，－1)∪[2，＋∞）8．已知定义域为R 的函数f (x )在区间(－∞，5)上单调递减，对任意实数t ，都有f (5＋t )＝f (5－t )，那么下列式子一定成立的是 （ ） A ．f (－1)＜f (9)＜f (13) B ．f (13)＜f (9)＜f (－1) C ．f (9)＜f (－1)＜f (13) D ．f (13)＜f (－1)＜f (9) 9．函数)2()(||)(x x x g x x f -==和的递增区间依次是（ ）A ．]1,(],0,(-∞-∞B ．),1[],0,(+∞-∞C ．]1,(),,0[-∞+∞D ),1[),,0[+∞+∞10．已知函数()()2212f x x a x =+-+在区间(]4,∞-上是减函数，则实数a 的取值范围是（ ） A ．a ≤3 B ．a ≥－3 C ．a ≤5 D ．a ≥3 11．已知f (x )在区间(－∞，＋∞)上是增函数，a 、b ∈R 且a ＋b ≤0，则下列不等式中正确的是（ ） A ．f (a )＋f (b )≤－f (a )＋f (b )］ B ．f (a )＋f (b )≤f (－a )＋f (－b ) C ．f (a )＋f (b )≥－f (a )＋f (b )］ D ．f (a )＋f (b )≥f (－a )＋f (－b )12．定义在R 上的函数y =f (x )在(－∞，2)上是增函数，且y =f (x ＋2)图象的对称轴是x =0，则 （ ） A ．f (－1)＜f (3) B ．f (0)＞f (3) C ．f (－1)=f (－3) D ．f (2)＜f (3) 二、填空题：13．函数y =(x －1)-2的减区间是___ _． 14．函数y =x －2x -1＋2的值域为__ ___． 15、设()y f x =是R 上的减函数，则()3y fx =-的单调递减区间为 .16、函数f (x ) = ax 2＋4(a ＋1)x －3在[2，＋∞]上递减，则a 的取值范围是__ ． 三、解答题：17．f (x )是定义在( 0，＋∞)上的增函数，且f (yx) = f (x )－f (y ) （1）求f (1)的值．（2）若f (6)= 1，解不等式 f ( x ＋3 )－f (x1) ＜2 ．18．函数f (x )=－x 3＋1在R 上是否具有单调性？如果具有单调性，它在R 上是增函数还是减函数？试证明你的结论．19．试讨论函数f (x )=21x -在区间［－1，1］上的单调性．20．设函数f (x )=12+x －ax ，(a ＞0)，试确定：当a 取什么值时，函数f (x )在0，＋∞)上为单调函数．21．已知f (x )是定义在(－2，2)上的减函数，并且f (m －1)－f (1－2m )＞0，求实数m 的取值范围．22．已知函数f (x )=xax x ++22，x ∈［1，＋∞］（1）当a =21时，求函数f (x )的最小值；（2）若对任意x ∈[1，＋∞)，f (x )＞0恒成立，试求实数a 的取值范围．参考答案一、选择题： CDBBD ADCCA BA二、填空题：13. (1，＋∞)， 14. (－∞，3)，15.[)3,+∞， ⎥⎦⎤ ⎝⎛-∞-21,三、解答题：17.解析：①在等式中0≠=y x 令，则f (1)=0．②在等式中令x=36，y=6则.2)6(2)36(),6()36()636(==∴-=f f f f f 故原不等式为：),36()1()3(f xf x f <-+即f [x (x ＋3)]＜f (36)， 又f (x )在(0，＋∞)上为增函数，故不等式等价于：.23153036)3(00103-<<⇒⎪⎪⎩⎪⎪⎨⎧<+<>>+x x x xx18.解析： f (x )在R 上具有单调性，且是单调减函数，证明如下：设x 1、x 2∈(－∞，＋∞)， x 1＜x 2 ，则f (x 1)=－x 13＋1， f (x 2)=－x 23＋1．f (x 1)－f (x 2)=x 23－x 13=(x 2－x 1)(x 12＋x 1x 2＋x 22)=(x 2－x 1)［(x 1＋22x )2＋43x 22］．∵x 1＜x 2，∴x 2－x 1＞0而(x 1＋22x )2＋43x 22＞0，∴f (x 1)＞f (x 2)．∴函数f (x )=－x 3＋1在(－∞，＋∞)上是减函数．19.解析： 设x 1、x 2∈－1，1］且x 1＜x 2，即－1≤x 1＜x 2≤1．f (x 1)－f (x 2)=211x -－221x -=2221222111)1()1(x x x x -+----=2221121211))((x x x x x x -+-+-∵x 2－x 1＞0，222111x x -+-＞0，∴当x 1＞0，x 2＞0时，x 1＋x 2＞0，那么f (x 1)＞f (x 2)． 当x 1＜0，x 2＜0时，x 1＋x 2＜0，那么f (x 1)＜f (x 2)．故f (x )=21x -在区间［－1，0］上是增函数，f (x )=21x -在区间［0，1］上是减函数． 20.解析：任取x 1、x 2∈0，＋)∞且x 1＜x 2，则f (x 1)－f (x 2)=121+x －122+x －a (x 1－x 2)=1122212221+++-x x x x －a (x 1－x 2)=(x 1－x 2)(11222121++++x x x x －a )(1)当a ≥1时，∵11222121++++x x x x ＜1，又∵x 1－x 2＜0，∴f (x 1)－f (x 2)＞0，即f (x 1)＞f (x 2)∴a ≥1时，函数f (x )在区间［0，＋∞)上为减函数． (2)当0＜a ＜1时，在区间［0，＋∞］上存在x 1=0，x 2=212aa-，满足f (x 1)=f (x 2)=1 ∴0＜a ＜1时，f (x )在［０，＋)∞上不是单调函数 注： ①判断单调性常规思路为定义法； ②变形过程中11222121++++x x x x ＜1利用了121+x ＞|x 1|≥x 1;122+x ＞x 2；③从a 的范围看还须讨论0＜a ＜1时f (x )的单调性，这也是数学严谨性的体现．21.解析： ∵f (x )在(－2，2)上是减函数∴由f (m －1)－f (1－2m )＞0，得f (m －1)＞f (1－2m )∴⎪⎪⎪⎩⎪⎪⎪⎨⎧<<<-<<-⎪⎩⎪⎨⎧-<-<-<-<-<-32232131211,2212212m m m m m m m 即 解得3221<<-m ，∴m 的取值范围是(－32,21)22.解析： (1)当a =21时，f (x )=x ＋x21＋2，x ∈1，＋∞) 设x 2＞x 1≥1，则f (x 2)－f (x 1)=x 2＋1122121x x x --=(x 2－x 1)＋21212x x x x -=(x 2－x 1)(1－2121x x ) ∵x 2＞x 1≥1，x 2－x 1＞0，1－2121x x ＞0，则f (x 2)＞f (x 1) 可知f (x )在［1，＋∞)上是增函数．∴f (x )在区间［1，＋∞)上的最小值为f (1)=27． (2)在区间［1，＋∞)上，f (x )=xax x ++22＞0恒成立⇔x 2＋2x ＋a ＞0恒成立设y =x 2＋2x ＋a ，x ∈1，＋∞)，由y =(x ＋1)2＋a －1可知其在[1，＋∞)上是增函数， 当x =1时，y min =3＋a ，于是当且仅当y min =3＋a ＞0时函数f (x )＞0恒成立．故a ＞－3．。

§1.2.1 函数的概念¤知识要点：1. 设A、B是非空的数集，如果按某个确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数y和它对应，那么就称f：A→B为从集合A到集合B的一个函数，记作y=()f x，x A∈．其中，x叫自变量，x的取值范围A叫作定义域，与x的值对应的y值叫函数值，函数值的集合{()|}f x x A∈叫值域.2. 设a、b是两个实数，且a<b，则：{x|a≤x≤b}＝[a,b] 叫闭区间； {x|a<x<b}＝(a,b) 叫开区间；{x|a≤x<b}＝[,)a b， {x|a<x≤b}＝(,]a b，都叫半开半闭区间.符号：“∞”读“无穷大”；“－∞”读“负无穷大”；“+∞”读“正无穷大”. 则{|}(,)x x a a>=+∞，{|}[,)x x a a≥=+∞，{|}(,)x x b b<=-∞，{|}(,]x x b b≤=-∞，(,)R=-∞+∞.3. 决定函数的三个要素是定义域、值域和对应法则. 当且仅当函数定义域、对应法则分别相同时，函数才是同一函数.¤例题精讲：【例1】求下列函数的定义域：（1）121yx=+-；（2）y=.解：（1）由210x+-≠，解得1x≠-且3x≠-，所以原函数定义域为(,3)(3,1)(1,)-∞----+∞U U.（2）由3020x-≥⎧⎪≠，解得3x≥且9x≠，所以原函数定义域为[3,9)(9,)+∞U.【例2】已知函数1(1xf xx-=+. 求：（1）(2)f的值；（2）()f x的表达式解：（1）由121xx-=+，解得13x=-，所以1(2)3f=-.（2）设11xtx-=+，解得11txt-=+，所以1()1tf tt-=+，即1()1xf xx-=+.点评：此题解法中突出了换元法的思想. 这类问题的函数式没有直接给出，称为抽象函数的研究，常常需要结合换元法、特值代入、方程思想等.【例3】已知函数22(),1xf x x Rx=∈+.（1）求1()(f x fx+的值；（2）计算：111(1)(2)(3)(4)()(()234f f f f f f f++++++.解：（1）由2222222221111()(1111111x x xxf x fx x x x xx++=+=+==+++++.（2）原式11117(1)((2)(((3)(((4)(323422f f f f f f f=++++++=+=点评：对规律的发现，能使我们实施巧算. 正确探索出前一问的结论，是解答后一问的关键.§1.2.2 函数的表示法¤知识要点：1. 函数有三种表示方法：解析法（用数学表达式表示两个变量之间的对应关系，优点：简明，给自变量可求函数值）；图象法（用图象表示两个变量的对应关系，优点：直观形象，反应变化趋势）；列表法（列出表格表示两个变量之间的对应关系，优点：不需计算就可看出函数值）.2. 分段函数的表示法与意义（一个函数，不同范围的x ，对应法则不同）.3. 一般地，设A 、B 是两个非空的集合，如果按某一个确定的对应法则f ，使对于集合A 中的任意一个元素x ，在集合B 中都有唯一确定的元素y 与之对应，那么就称对应:f A B →为从集合A 到集合B 的一个映射（mapping ）．记作“:f A B →”.判别一个对应是否映射的关键：A 中任意，B 中唯一；对应法则f . ¤例题精讲：【例1】如图，有一块边长为a 的正方形铁皮，将其四个角各截去一个边长为x 的小正方形，然后折成一个无盖的盒子，写出体积V 以x 为自变量的函数式是_____，这个函数的定义域为_______．解：盒子的高为x ，长、宽为2a x －，所以体积为V ＝2(2)x a x －.又由20a x >－，解得2a x <.所以，体积V 以x 为自变量的函数式是2(2)V x a x =－，定义域为{|0}2a x x <<.【例2】已知f (x )=333322x x x x-⎧++⎪⎨+⎪⎩(,1)(1,)x x ∈-∞∈+∞，求f [f (0)]的值.解：∵ 0(,1)∈-∞， ∴ f (0)=32. 又 ∵ 32>1，∴ f (32)=(32)3+(32)-3=2+12=52，即f [f (0)]=52.【例3】画出下列函数的图象：（1）|2|y x =-； （教材P 26 练习题3） （2）|1||24|y x x =-++.解：（1）由绝对值的概念，有2,2|2|2,2x x y x x x -≥⎧=-=⎨-<⎩.所以，函数|2|y x =-的图象如右图所示.（2）33,1|1||24|5,2133,2x x y x x x x x x +>⎧⎪=-++=+-≤≤⎨⎪--<-⎩，所以，函数|1||24|y x x =-++的图象如右图所示.点评：含有绝对值的函数式，可以采用分零点讨论去绝对值的方法，将函数式化为分段函数，然后根据定义域的分段情况，选择相应的解析式作出函数图象.【例4】函数()[]f x x =的函数值表示不超过x 的最大整数，例如[ 3.5]4-=-，[2.1]2=，当( 2.5,3]x ∈-时，写出()f x 的解析式，并作出函数的图象.解：3, 2.522,211,10()0,011,122,233,3x x x f x x x x x --<<-⎧⎪--≤<-⎪--≤<⎪=≤<⎨⎪≤<⎪≤<⎪=⎩. 函数图象如右： 点评：解题关键是理解符号[]m 的概念，抓住分段函数的对应函数式.§1.3.1 函数的单调性¤知识要点：1. 增函数：设函数y =f (x )的定义域为I ，如果对于定义域I 内的某个区间D 内的任意两个自变量x 1，x 2，当x 1<x 2时，都有f (x 1)<f (x 2)，那么就说f (x )在区间D 上是增函数（increasing function ）. 仿照增函数的定义可定义减函数.2. 如果函数f (x )在某个区间D 上是增函数或减函数，就说f (x )在这一区间上具有（严格的）单调性，区间D 叫f(x )的单调区间. 在单调区间上，增函数的图象是从左向右是上升的（如右图1），减函数的图象从左向右是下降的（如右图2）. 由此，可以直观观察函数图象上升与下降的变化趋势，得到函数的单调区间及单调性.3. 判断单调性的步骤：设x 1、x 2∈给定区间，且x 1<x 2；→计算f (x 1)－f (x 2) →判断符号→下结论.¤例题精讲：【例1】试用函数单调性的定义判断函数2()1x f x x =-在区间（0，1）上的单调性.解：任取12,x x ∈(0,1)，且12x x <. 则1221121212222()()()11(1)(1)x x x x f x f x x x x x --=-=----. 由于1201x x <<<，110x -<，210x -<，210x x ->，故12()()0f x f x ->，即12()()f x f x >.所以，函数2()1xf x x =-在（0，1）上是减函数. 【例2】求下列函数的单调区间： （1）|1||24|y x x =-++；（2）22||3y x x =-++.解：（1）33,1|1||24|5,2133,2x x y x x x x x x +>⎧⎪=-++=+-≤≤⎨⎪--<-⎩，其图象如右.由图可知，函数在[2,)-+∞上是增函数，在(,2]-∞-上是减函数.（2）22223,02||323,0x x x y x x x x x ⎧-++≥⎪=-++=⎨--+<⎪⎩，其图象如右.由图可知，函数在(,1]-∞-、[0,1]上是增函数，在[1,0]-、[1,)+∞上是减函数.点评：函数式中含有绝对值，可以采用分零点讨论去绝对值的方法，将函数式化为分段函数. 第2小题也可以由偶函数的对称性，先作y 轴右侧的图象，并把y 轴右侧的图象对折到左侧，得到(||)f x 的图象. 由图象研究单调性，关键在于正确作出函数图象.【例3】已知31()2x f x x +=+，指出()f x 的单调区间.解：∵ 3(2)55()322x f x x x +--==+++，∴ 把5()g x x-=的图象沿x 轴方向向左平移2个单位，再沿y 轴向上平移3个单位，得到()f x 的图象，如图所示.由图象得()f x 在(,2)-∞-单调递增，在(2,)-+∞上单调递增.点评：变形后结合平移知识，由平移变换得到一类分式函数的图象. 需知()f x a b ++平移变换规律.§1.3.1 函数最大（小）值¤知识要点：1. 定义最大值：设函数()y f x =的定义域为I ，如果存在实数M 满足：对于任意的x ∈I ，都有()f x ≤M ；存在x 0∈I ，使得0()f x = M . 那么，称M 是函数()y f x =的最大值（Maximum Value ）. 仿照最大值定义，可以给出最小值（Minimum Value ）的定义.2. 配方法：研究二次函数2(0)y ax bx c a =++≠的最大（小）值，先配方成224()24b ac b y a x a a -=++后，当0a >时，函数取最小值为244ac b a-；当0a <时，函数取最大值244ac b a-.3. 单调法：一些函数的单调性，比较容易观察出来，或者可以先证明出函数的单调性，再利用函数的单调性求函数的最大值或最小值.4. 图象法：先作出其函数图象后，然后观察图象得到函数的最大值或最小值. ¤例题精讲：【例1】求函数261y x x =++的最大值.解：配方为2613()24y x =++，由2133()244x ++≥，得260813()24x <≤++. 所以函数的最大值为8.【例3】求函数21y x x =+-的最小值.解：此函数的定义域为[)1,+∞，且函数在定义域上是增函数， 所以当1x =时，min 2112y =+-=，函数的最小值为2.点评：形如y ax b cx d =+±+的函数最大值或最小值，可以用单调性法研究，也可以用换元法研究.【另解】令1x t -=，则0t ≥，21x t =+，所以22115222()48y t t t =++=++，在0t ≥时是增函数，当0t =时，min 2y =，故函数的最小值为2.【例4】求下列函数的最大值和最小值：（1）25332,[,]22y x x x =--∈-； （2）|1||2|y x x =+--.解：（1）二次函数232y x x =--的对称轴为2bx a=-，即1x =-.画出函数的图象，由图可知，当1x =-时，max 4y =； 当32x =时，min 94y =-. 所以函数25332,[,]22y x x x =--∈-的最大值为4,最小值为94-.（2） 3 (2)|1||2|2 1 (12)3 (1)x y x x x x x ≥⎧⎪=+--=--<<⎨⎪-≤-⎩.作出函数的图象，由图可知，[3,3]y ∈-. 所以函数的最大值为3, 最小值为-3.点评：二次函数在闭区间上的最大值或最小值，常根据闭区间与对称轴的关系，结合图象进行分析. 含绝对值的函数，常分零点讨论去绝对值，转化为分段函数进行研究. 分段函数的图象注意分段作出.。

高中数学必修一 3.1函数与方程练习题及答案上述函数是幕函数的个数是 ( A. 0个 B.1个 C.2个 D.3个A. 有且仅有一个根B. 至多有一个根C. 至少有一个根D.以上结论都不对A.14400亩B . 172800亩C .17280 亩D . 20736亩8. 若函数f x 既是幕函数又是反比例函数 ，则这个函数是f X = ________9. 幕函数f(x)的图象过点⑶丿27)，则f (x)的解析式是 ______________________2.已知f(x)唯一的零点在区间(1,3)、(1,4)、 (1,5)内，那么下面命题错误的(A.函数 f(x)在(1,2)或 2,3内有零点 B.函数 f(x)在(3,5)内无零点 C 屈数 f (X )在(2,5)内有零点 D.函数 f(x)在(2,4)内不一定有零点 3.若a0,b 0, ab 1 2 ，则l(log a b log 1 alog a blog 1 a A .2B. 2log a b log 1 alog a b log 1 aC . 2D.24. 求函数 f(x) 2x33x 1零点的个数为 D. 4C. 3( )ab与A. 1B. 2 log 1 a ln 2 log 】a2的关系是5.已知函数yf(x)有反函数，则方程f(x) 0(26.如果二次函数y x mx (m3)有两个不同的零点，则 m 的取值范围是(A. 2,6B. 2,6C.2,6D. , 2 U 6 ,7.某林场计划第一年造林10000亩,以后每年比前一年多造林 20%，则第四年造林(1.若y x2八八心i,y(x 1)2,y x,y a x (a 1)10. 用二分法”求方程X 3 2x 5 °在区间23］内的实根，取区间中点为 X 。

2.5，那么下一个有根的区间是 __________________11. 函数f （x ） lnx X 2的零点个数为 _________________ 12.设函数y f （x ）的图象在a,b 上连续，若满足 ________________ ，方程f （x ） °在a,b 上有实根.1f （x ） x — x 113.用定义证明：函数x在减少1个，为了获得最大利润，则此商品的最佳售价应为多少?上是增函数14.设x1与x 2分别是实系数方程ax 2 bx c ° 禾a 2OX 0，求证：方程畀bx C°有仅有一根介于x1和x2之间.15.函数f(x)x 22ax 1 a在区间°」上有最大值2，求实数a 的值16.某商品进货单价为 4°元，若销售5°元，可卖出5°个，如果销售单价每涨1元，销售量就17.函数y xA.是奇函数，且在R 上是单调增函数B. 是奇函数，且在R 上是单调减函数C.是偶函数，且在R 上是单调增函数D. 是偶函数，且在R 上是单调减函数18.已知a log2 °.3,b2,c 0.2 ，则a,b,c 的大小关系是（22. 一个高中研究性学习小组对本地区2000年至2002年快餐公司发展情况进行了调查，制成了该地区快餐公司个数情况的条形图和快餐公司盒饭年销售量的平均数情况条形图（如图） ，根据图中提供的信息可以得出这三年中该地区每年平均销售盒饭 ___________ 万盒.A . a b cB . cC.a c bD.b19.函数f(x) x 5x 3的实数解落在的区间是（20.函数 根的和为C 」2,3]D .【3,4]f（x ）对一切实数x ），并且方程f （x ）有三个实根，则这三个实21.若函数f(x) 4x x 2a的零点个数为3，则a126. 函数y = x +1的单调区间为 _____________ .27. 函数f （x ）= 2X 2— 3 | x |的单调减区间是 ____________x log 2 x23.已知 2x 256且2 ,求函数住） x 仮 log22 g’T 的最大值和最小值.224.函数y = = x - 6x + 10在区间( 2, 4）上是（A.递减函数B .递增函数 C. 先递减再递增D. 选递增再递减.25.函数 f (x )=- x 2 + 2 (a - 1) x + 2在（―汽 4） 上是增函数，则a 的范围是（ A. a >5B . a > 3C. a w 3D. a w- 528. 确定函数y = x + x（x >0）的单调区间，并用定义证明.29. 快艇和轮船分别从A地和C地同时开出，如右图，各沿箭头方向航行，快艇和轮船的速度分别是45千米/时和15千米/时，已知AO 150千米，经过多少时间后，快艇和轮船之间的距离最短？30. 设f (x)是定义在R上的增函数，f (xy)= f (x) + f(y), f (3)= 1,求解不等式f (x) + f(x- 2)> 1.2答案1. C. y x ,y X 是幕函数 2. C •唯一的零点必须在区间（1,3），而不在3,5log 1 a ln 2 0,得0 a 1,b1log a b 0,log 1 a 03. A. 224 C f (x) 2x 33x 1 2x 32x x21 2x(x 1) (x 1)(x 1)(2x 2 2x 1), 2x 2 2x1 0显然有两个实数根，共二个;5. B.可以有一个实数根，例如 y X 1，也可以没有实数根,例如y2X6. D. 2m 4(m 3)0,m 6或 m 237 C 10000(1 0.2)1728018. x 设 f (x) x ,则 139f(x)仮3 f (x) x ,图象过点(3,^27)，3丁27 3,3310. [2,2.5)令 f (x) x 2x 5, f(2) 1 0, f (2.5) 2.5 1011. 2分别作出f(x) ln x , g(x) x 2的图象；12. f （a ）f （b ）0见课本的定理内容1 f(X 2)(捲 X 2)(1 )x-|x 2即 f(x 1) f (X 2)1 x-i13.证明：设X 2, f (xj2f(x) X —• ••函数X在上是增函数xa 14.解：令 f(x) -X2bx c,由题意可知2ax1bx 1 c 2 0, ax 2bx2c 0ax 22, f(x 1) a 2bx 1 ca 2 2a 2bx 1 c ax 12, bx 2 c尹2X1ax 1尹f(X 2)a 2 ,a 223a 2x 2 bxcx 2 ax 2 2~2 X2,因为a0,X 1 0,X 215.解：对称轴x a ，所以a40x 50017. A. 18. C. 19. B.当x 20时,y取得最大值，所以应定价为f( x) ( x)3a log 2 0.3 0,b f (0) 3 0, f(1) 70元X 3 f (x)为奇函数且为增函数2°11,c 1 0, f(2)0.21.3 131 0, f(1)f(2)320. 2对称轴为1x _2，可见 2是个实根，另两个根关于1 2对称21. 4 作出函数x 2 4x与函数y 4的图象，发现它们恰有3个交点.f (X 1)f(X 2)0，即方程 2-x 2 bx有仅有一根介于X 2之间.当a 0, 0,1是f(x)的递减区间,f (x)max f(0) 当a 1, 0,1是f (X )的递增区间,f(x)maxf(1) a 2f (x)max f (a) aa 1 2,a1矛盾;16•解: 设最佳售价为(50 x)元,最大利润为y 元,y (50x)(50 x)(50 x) 4022. 85 2000年 30 1.0 30 (万) ； 2001 年 45 2.0 90 (万)；-30 90 135 x ------------------- 2002年：90 匸5 135 (万) ;31 23.解：由 2x 256 得 x 8 , log 2x 3 即 2f(x) (log 2 x 1)(log 2X 2) (log 2 x 3)222 _____________________24. C 解析：本题可以作出函数 y = x - 6x + 10的图象，根据图象可知函数在(2, 4) 上是先递减再递 增. 25. A 解析：本题作出函数 f ( x )=- x 2 + 2 ( a - 1) x + 2的图象，可知此函数图象的对称轴是x = a—1,由图象可知，当 a -1 >4，即当 a >5时，函数 f (x )=- x 2 + 2 (a - 1) x + 2在(一^, 4)上 是增函数.26. ( — 8, — 1) , (- 1 ,+◎3327. :0,4L (-m ,- 4 )28. 解：本题可利用计算机作出该函数的图象，通过图象求得单调区间，最后用单调性的定义证明. 答案：增区间(1,+8)，减区间(0, 1).29. 解：设经过x 小时后快艇和轮船之间的距离最短，距离设为 y ,y = .. (150-45x)2 + (15x)2 (0<x3 ，可求得当x = 3时，y 有最小值.答案：3小时.30. 解：由条件可得 f (x )+ f (x - 2)= f : x (x - 2)], 1 = f (3).所以 f [ x (x - 2) > f (3), 又f ( x )是定义在R 上的增函数，所以有x ( x - 2) > 3，可解得x > 3或x <- 1. 答案：x > 3或x <- 1.当log2x3f (x ) imil 2min14 当 log 2 x 3, f (X )max285 (万)log 2x 3。

〔数学 1 必修〕函数及其表示一、选择题1．判断以下各组中的两个函数是同一函数的为〔 〕⑴ y 1(x 3)( x 5)x 5 ；x 3 ， y 2⑵ y 1 x 1 x 1， y 2( x 1)( x 1) ；⑶ f ( x)x ，g( x)x 2 ；⑷f ( x)3x 4 x3，F ( x) x 3 x 1 ；⑸ f 1 ( x)( 2x 5) 2 ， f 2 (x) 2x 5 。

A ．⑴、⑵B ．⑵、⑶C ．⑷D ．⑶、⑸2f ( x) 的图象与直线x 1的公共点数目是〔〕．函数 yA ． 1B ． 0C ． 0或 1 1 2D ． 或3．会集A1,2,3, k , B4,7, a 4 , a 23a ，且 aN * , x A, y B使 B 中元素 y 3x1 和 A 中的元素 x 对应，那么 a, k 的值分别为〔 〕A ． 2,3B ． 3,4C ． 3,5D ． 2,5x 2( x1)4． f ( x)x 2 ( 1 x 2) ，假设 f (x) 3 ，那么 x 的值是〔〕2x( x2)A ． 1B ．1或3C ．1， 3或3D ．3225．为了获取函数 yf ( 2x) 的图象，可以把函数y f (1 2x) 的图象合适平移，这个平移是〔〕11个单位A ．沿 x 轴向右平移个单位B ．沿 x 轴向右平移2C1D1个单位．沿 x 轴向左平移个单位．沿 x 轴向左平移26．设 f ( x)x 2,(x 10)那么 f(5)的值为〔〕f [ f ( x 6)], ( x 10)A ．10B ． 11C ． 12D ．13二、填空题1 x1(x0),1．设函数f (x)2假设 f (a)a. 那么实数 a 的取值范围是。

1( x0).x2．函数y x2的定义域。

x243．假设二次函数y ax2bx c 的图象与x轴交于 A( 2,0), B(4,0)，且函数的最大值为9，那么这个二次函数的表达式是。

高一数学必修一函数专题(教师版)一.函数的奇偶性.(1)具有奇偶性的函数的定义域的特征：定义域必须关于原点对称！为此确定函数的奇偶性时，务必先判定函数定义域是否关于原点对称•(2)确定函数奇偶性的常用方法(若所给函数的解析式较为复杂，应先化简，再判断其奇偶性)：①定义法；f(x) f( x) 0②利用函数奇偶性定义的等价形式：f( x) 1( f(x) 0).f (x)③图像法：奇函数的图象关于原点对称;偶函数的图象关于y轴对称.(3)函数奇偶性的性质：①奇函数在关于原点对称的区间上若有单调性，则其单调性完全相同；偶函数在关于原点对称的区间上若有单调性，则其单调性恰恰相反•②若f (x)为偶函数，贝U f( x) f (x) f (| x |).③若奇函数f(x)定义域中含有0,则必有f(0) 0.④奇函数的图象关于原点对称;偶函数的图象关于y轴对称.二.函数的单调性1. 函数单调性的定义：(1)如果函数f x对区间D内的任意x-! ,x2，当x1 x2时都有f % f x2，则f x在D内是增函数；当x1 x2时都有f为f x2，则f x在D内是减函数.(2)设函数y f (x)在某区间D内可导，若f X 0，则y f (x)在D内是增函数；若f x 0，则y f (x)在D内是减函数.2•单调性的定义的等价形式：(1)设x1 ,x2 a,b，那么匚勺——^-x^ 0 f x在a,b上是增函数；x1 x2(2) --------------------------------------- 设x1 ,x2 a,b，那么f x2 0 f x 在a,b 上是减函数；x1 x23.证明或判断函数单调性的方法：(1) 定义法：设元作差变形判断符号给出结论•其关键是作差变形，为了便于判断差的符号，通常将差变成因式连乘积、平方和等形式，再结合变量的范围，假设的两个变量的大小关系及不等式的性质作出判断；⑵复合函数单调性的判断方法：即“同增异减”法，即内层函数和外层函数的单调性相同，则复合函数为增函数；若相反，则复合函数为减函数•解决问题的关键是区分好内外层函数，掌握常用基本函数的单调性；(3)图象法：利用数形结合思想，画出函数的草图，直接得到函数的单调性；(4)导数法：利用导函数的正负来确定原函数的单调性，是最常用的方法.(5)利用常用结论判断：①奇函数在对称的单调区间内有相同的单调性，偶函数在对称的单调区间内有相反的单调性；②互为反函数的两个函数具有相同的单调性；③在公共定义域内，增函数f(x)增函数g(x)是增函数；减函数f(x)减函数g(x)是减函数；增函数f (x)减函数g(x)是增函数；减函数f (x)增函数g(x)是减函数；④复合函数法：复合函数单调性的特点是同增异减,特别提醒：求单调区间时，勿忘定义域，三.函数的周期性.(1)类比“三角函数图像”得：①若y f (x)图像有两条对称轴x a,x b(a b)，则y f (x)必是周期函数，且一周期为T 2|a b| ；②若y f (x)图像有两个对称中心A(a,O), B(b,O)(a b)，则y f(x)是周期函数，且一周期为T 2|a b| ；③如果函数y f (x)的图像有一个对称中心A(a,O)和一条对称轴x b(a b)，则函数y f(x)必是周期函数，且一周期为T 4|a b| ；(2)由周期函数的定义“函数f(x)满足f x f a x (a 0)，则f(x)是周期为a的周期函数”得：函数f (x)满足 f x f a x，则f(x)是周期为2a的周期函数。