设有一以理想气体为工作物质的热机循环

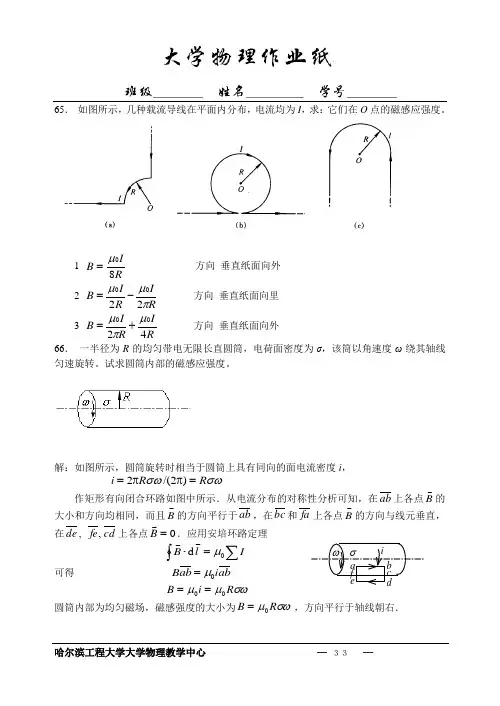
65． 如图所示，几种载流导线在平面内分布，电流均为I ，求：它们在O 点的磁感应强度。

1 RIB 80μ=方向 垂直纸面向外2 R I R I B πμμ2200-= 方向 垂直纸面向里 3 RI R I B 4200μπμ+= 方向 垂直纸面向外 66． 一半径为R 的均匀带电无限长直圆筒，电荷面密度为σ，该筒以角速度ω绕其轴线匀速旋转。

试求圆筒内部的磁感应强度。

解：如图所示，圆筒旋转时相当于圆筒上具有同向的面电流密度i ， σωσωR R i =ππ=)2/(2作矩形有向闭合环路如图中所示．从电流分布的对称性分析可知，在ab 上各点B的大小和方向均相同，而且B 的方向平行于ab ，在bc 和fa 上各点B的方向与线元垂直，在de , cd fe ,上各点0=B．应用安培环路定理∑⎰⋅=I l B 0d μ 可得 ab i ab B 0μ= σωμμR i B 00==圆筒内部为均匀磁场，磁感强度的大小为σωμR B 0=，方向平行于轴线朝右．i ω σc deab f67．在半径为R 的长直金属圆柱体内部挖去一个半径为r 的长直圆柱体，两柱体轴线平行，其间距为a （如图）。

今在此导体内通以电流I ，电流在截面上均匀分布，求：空心部分轴线上O ' 点的磁感应强度的大小。

解：)(22r R IJ -=π10121r k J B ⨯=μ 20221r k J B ⨯-=μj Ja O O k J r r k J B B B 021********21)(21μμμ=⨯=-⨯=+=j r R IaB )(2220-=πμ68．一无限长圆柱形铜导体,半径为R ,通以均匀分布的I 今取一矩形平面S （长为L ，宽为2R ），位置如图，求：通过该矩形平面的磁通量。

解：在圆柱体内部与导体中心轴线相距为r 处的磁感强度的大小，由安培环路定律可得：)(220R r r R IB ≤π=μ因而，穿过导体内画斜线部分平面的磁通Φ1为⎰⎰⋅==S B S B d d 1 Φr rL R I Rd 2020⎰π=μπ=40LIμ在圆形导体外，与导体中心轴线相距r 处的磁感强度大小为 )(20R r rIB >π=μ因而，穿过导体外画斜线部分平面的磁通Φ2为⎰⋅=S B d 2Φr r IL R Rd 220⎰π=μ2ln 20π=ILμ穿过整个矩形平面的磁通量 21ΦΦΦ+=π=40LIμ2ln 20π+ILμ69．如图所示，载有电流I 1和I 2的无限长直导线相互平行，相距3r ，今有载有电流I 3的导线MN = r 水平放置，其两端M 、N 分别与I 1、I 2距离均为r ，三导线共面，求：导线MN 所受的磁场力的大小与方向。

第五章 热力学基础5－1 在水面下50.0 m 深的湖底处（温度为4.0℃），有一个体积为1.0×10-5 m 3的空气泡升到湖面上来，若湖面的温度为17.0℃，求气泡到达湖面的体积。

（大气压P 0 = 1.013×105 Pa ） 分析：将气泡看成是一定量的理想气体，它位于湖底和上升至湖面代表两个不同的平衡状态。

利用理想气体物态方程即可求解本题。

位于湖底时，气泡内的压强可用公式gh p p ρ+=0求出，其中ρ为水的密度（常取ρ = 1.0⨯103 kg·m -3）。

解：设气泡在湖底和湖面的状态参量分别为（p 1，V 1，T 1）和（p 2，V 2，T 2）。

由分析知湖底处压强为ghp gh p p ρρ+=+=021。

利用理想气体的物态方程可得空气泡到达湖面的体积为()3510120121212m 1011.6-⨯=+==T p V T gh p T p V T p V ρ5－2 氧气瓶的容积为3.2×10-2 m 3，其中氧气的压强为1.30×107 Pa ，氧气厂规定压强降到1.00×106 Pa 时，就应重新充气，以免经常洗瓶。

某小型吹玻璃车间，平均每天用去0.40 m 3 压强为1.01×105 Pa 的氧气，问一瓶氧气能用多少天？（设使用过程中温度不变） 分析：由于使用条件的限制，瓶中氧气不可能完全被使用。

从氧气质量的角度来分析。

利用理想气体物态方程pV = mRT /M 可以分别计算出每天使用氧气的质量m 3和可供使用的氧气总质量（即原瓶中氧气的总质量m 1和需充气时瓶中剩余氧气的质量m 2之差），从而可求得使用天数321/)(m m m n -=。

解：根据分析有RT V Mp m RT V Mp m RT V Mp m 333122111===；；则一瓶氧气可用天数()()5.933121321=-=-=V p V p p m m m n5－3 一抽气机转速ω=400r ּmin -1，抽气机每分钟能抽出气体20升。

以实际气体为工作物质的卡诺循环卡诺循环是一种热力学循环，用于描述理想的热机工作原理。

该循环是由19世纪法国物理学家尼古拉·卡诺提出的，通过理论上的推导说明了热机的最大效率与热机内部参数之间的关系。

卡诺循环的一个关键要素是工作物质，它需要是可逆的理想气体。

本文将介绍使用实际气体作为工作物质的卡诺循环。

实际气体的特性：实际气体通常具有非理想气体的特性，这意味着它们的行为不能完全符合理想气体定律。

实际气体的特性包括：1. 对压缩和膨胀的数据不敏感。

也就是说，在相同压力水平下，实际气体的体积变化比理想气体小。

2. 具有摩擦和黏合力，从而导致能量损失。

3. 在高压和低温下，实际气体不一定保持气态状态。

在卡诺循环中，使用理想气体和实际气体的最大区别是可逆过程和不可逆过程之间的关系。

理论上，只有可逆过程才存在于理想气体中。

而实际气体不完全符合这一点，因为存在着一些不可逆过程，导致热能的损失。

卡诺循环的理论原理：卡诺循环是一种理想的热力学循环，其目的在于说明热机最大化工作所达到的效率。

卡诺循环由四个过程组成：等温膨胀、绝热膨胀、等温压缩和绝热压缩。

这些过程描述了热机如何从热源吸收热能和向热源放热。

在卡诺循环中，使用的工作物质通常是理想气体，因为它是一种可逆热机。

但如果使用实际气体作为工作物质，卡诺循环的效率就会降低，因为实际气体通常包含不可逆过程。

卡诺循环的性能参数：卡诺循环的性能参数包括效率和热机内部温度。

1. 效率：卡诺循环的效率是指热机工作过程中所利用的热能与热源提供的总能量之比。

效率公式为：η = (T1 - T2) / T1其中，T1为热机工作时的高温热源温度，T2为热机工作时的低温热源温度。

2. 温度：在卡诺循环中，热机内部有两种温度。

一个是热源的温度，另一个是热机的内部温度。

热机内部的温度高于低温热源，但低于高温热源。

温度公式为：T1 - T2 = Q1 / C1= Q2 / C2其中，Q1为高温热源提供的能量，Q2为低温热源提供的能量，C1和C2分别为热机工作过程中的两个热容。

第1章 温度习题答案一、 选择题 1. D 2. B二、填空题1. Pa 31008.9⨯ K 4.90 C 08.182-三、计算题1. 解：漏掉的氢气的质量kg T Vp T V p R M m m m 32.0)(22211121=-=-=∆第2章 气体分子动理论答案一、选择题1. B解：两种气体开始时p 、V 、T 均相同，所以摩尔数也相同。

现在等容加热 V C MQ μ=△T ，R C R C V V 25,232H He ==由题意 μM Q =HeR 23⋅△T ＝ 6 J 所以 R M Q 252H ⋅=μ△T ＝(J)1063535H =⨯=e Q 。

2. C 解：由,)(,)(,He 222O 1112R MT V p R M T V p R MT pV ⋅=⋅==μμμ,,2121T T p p ==又 所以,21)()21He O 2==V V MM μμ（ 根据内能公式,2RT i M E ⋅=μ得二者内能之比为65352121=⋅=E E 3. B解：一个分子的平均平动动能为,23kT w =容器中气体分子的平均平动动能总和为3210410523232323-⨯⨯⨯⨯===⋅==pV RT M kT N Mw N W A μμ ＝3(J)。

4. C解：由RpVC E RT MpV T C ME VV ===得 ,μμ， 可见只有当V 不变时，E ~ p 才成正比。

5. D解：因为)(d v f NN =d v ，所以)(21212v f N mv v v ⋅⋅⎰d ⎰=21221v v mv v d N 表示在1v ~2v 速率间隔内的分子平动动能之和。

6. D 解：由,2,2122v n d z nd ππλ==体积不变时n 不变，而v ∝T ， 所以, 当T 增大时，λ不变而z 增大。

二、填空题1. 27.8×10-3 kg ⋅mol -1 解：由RT MpV μ=可得摩尔质量为523mol10013.1100.130031.8103.11⨯⨯⨯⨯⨯⨯====--p RT pV MRT M ρμ )m o l (k g 108.2713--⋅⨯=2. 1.28×10-7K 。

2019级电子信息工程学院物理学（师范）专业核心课程热学期末复习题解析1.定体温度计的测温泡浸在水的三相点槽内时，其中气体的压强为：pa 3106.7⨯。

（1）用温度计测量300K 得温度时，气体的压强是多少？ （2）当气体的压强为：Pa 3109.1⨯，待测温度是多少？ 解：（1）K p pp T tr16.273)(⨯=,pa p tr 3107.6⨯=，当K T 300=时带入解得： pa p 32.7358=；（2）当pa p 3101.9⨯=时，带入公式得：K T 371=。

2. 图示的两条曲线分别表示在相同温度下氧气和氢气分子的速率分布曲线。

请问哪一条曲线表示氧气分子的速率分布曲线？ 解：M RTmkTv p 22==，22H O M M >a 为氧气。

3.麦克斯韦速度分布函数是)(x f ，则s m v /100>的气体分子的平均速率v 为（⎰∞=100)(dv v f vv ）。

4.半径为r 密度为ρ的小球在黏度系数为η，密度为σ的液体中自由下沉，求稳定后小球的速度是（g r v )(922σρη-=）。

解析：稳定后受力平衡则：.)(92,346623g r v mg g r vr mg gV vr σρηπσπηρπη-=⇒=+⇒=+排液体 5. 如果理想气体按照C pV =3（C 为正数常量）的规律从1V 膨胀到2V ，则做功为（)11(22221V V C A -=）。

解析：).11(2222132121V V C A dV V C pdV A V V V V -=−−−→−==⎰⎰解出方程得：OEA B6. 某理想气体状态变化时，内能随体积的变化关系如图中AB 直线所示．A →B 表示的过程是（等压）过程。

解析：ννpVi U RT pV RT i U ⨯=⇒==2,2，从图中得出：aV U =，故为等压。

7. 有23molH (可视为理想气体），由423K 298K 加热到则此过程中U ∆为（7790.625J ）。

热学部分大练习一、填空题1. 相同温度下的1摩尔氧和2摩尔二氧化碳，对这两份气体，比较它们下列诸量的大小： （1）分子平均动能之比为_________________；（氧：二氧化碳） （2）分子平均平动动能之比为________________； （3）内能之比为____________________．2. 假设有一种气体，构成它的粒子服从以下速率分布率()()()⎩⎨⎧≥<<-=000 00)(v v v v v v Av v f式中A 为常量。

则用 v 0 定出的A =____________，平均速率=v __________________．3. 假设有N 个电子组成的电子气，其速率分布函数为f （v ）与v 的关系如图所示。

则A 的大小为________________，在速率0～900 m /s 间电子的平均速率为_____________。

4. 已知f (v )为麦克斯韦速率分布函数，N 为总分子数，则(1) 速率v > 100 m ·s -1的分子数占总分子数的百分比的表达式为_________；(2) 速率v > 100 m ·s -1的分子数的表达式为__________________．5. 图示曲线为处于同一温度T 时氦(原子量4)、氖(原子量20)和氩(原子量40)三种气体分子的速率分布曲线。

其中 曲线 (a) 是 气体分子的速率分布曲线； 曲线 (c) 是 气体分子的速率分布曲线．6. 当理想气体处于平衡态时，若气体分子速率分布函数为f (v )，则分子速率处于最概然速率v p 至∞范围内的概率△N / N ＝________________．7. 某理想气体，在温度T 1和T 2（T 1>T 2）时的麦克斯韦速率分布曲线如图所示，对应T 2的曲线应是__________，已知v 0是曲线Ⅱ的最可几速率，则曲线Ⅰ的最可几速率为____________。

Carnot cycle两个绝热过程和两个等温过程组成的循环。

1824年法国工程师S.卡诺在研究提高热机效率的过程中，设想了一种热机。

假定工作物质只同两个热源（高温热源和低温热源）交换热量，既没有散热也不存在摩擦，这种热机称为卡诺热机。

其循环过程称为卡诺循环。

卡诺循环的工作物质可以是理想气体，气、液二相系统，磁介质等。

循环若是可逆的，就称为可逆卡诺循环；若是不可逆的，就称为不可逆卡诺循环。

通常提到的卡诺循环，是指可逆卡诺循环。

卡诺循环中能量的转换情况可用图1表示。

工作物质从高温热源吸收热量Q1，一部分用于对外作功A，一部分热量Q2放给低温热源。

因为卡诺循环只同两个热源交换热量，所以可逆卡诺循环是由两个准静态等温过程和两个准静态绝热过程组成的。

图2是理想气体可逆卡诺循环的p－V图。

①等温膨胀，工作物质从温度为T1的热源吸收热量Q1，由状态(T1，V A)膨胀到状态(T1，V B)；②绝热膨胀，由状态(T1，V B)到状态(T2，V C)；③等温压缩，由状态(T2，V C)到状态(T2，V2)，工质放出热量Q2;④绝热压缩，由状态(T2，V2)到状态(T1，V A)，完成一个循环。

在此循环过程中，卡诺热机所作的功为A＝Q1-Q2，循环的效率而理想气体卡诺循环的效率则为，仅同两个热源的温度有关。

卡诺进一步提出：①在相同的高温热源和相同的低温热源之间工作的一切可逆热机，其效率都是，同工作物质无关。

②在相同的高温热源和相同的低温热源之间工作的一切不可逆热机，其效率都不可能大于可逆热机的效率。

以上两条统称为卡诺定理。

卡诺对该定理的证明是根据热质说理论和制造永动机不可能原理作出的。

直到开尔文和R.克劳修斯建立了热力学第二定律之后，卡诺定理才得到正确的证明。

卡诺循环和卡诺定理都具有很重要的理论和实践意义，对热力学第二定律的建立起了重要作用。

在卡诺定理的基础上还建立了同测温质以及测温属性无关的热力学温标，使温度测量建立在客观的基础上。

第1章 《热力学》习题解答1-1若一打足气的自行车内胎在7.0C 时轮胎中空气压强为54.010Pa ⨯，则在温度变为37.0C 时，轮胎内空气压强为多少？（设内胎容积不变）[解]：轮胎内的定质量空气做等容变化状态1 Pa P K T 511100.4,280⨯== 状态2：?,28022==P K T 由查理定律得Pa Pa P T T P T T P P 55112212121043.4100.4280310⨯=⨯⨯==⇒= 1-2 氧气瓶的容积为233.210m -⨯，其中氧气的压强为71.310Pa ⨯，氧气厂规定压强降到61.010Pa ⨯时，就应重新充气，以免经常洗瓶. 某小型吹玻璃车间平均每天用去30.40m 在51.0110Pa ⨯压强下的氧气，问一瓶氧气能用多少天？（设使用过程中温度不变）[解]：设氧气瓶的容积为320102.3m V -⨯=，使用过程的温度T 保持不变使用前氧气瓶中，氧气的压强为Pa P 71103.1,⨯= 根据克拉帕龙方程nRT PV =得： 使用前氧气瓶中，氧气的摩尔数为RTV P n 011,=氧气压强降到Pa P 62100.1,⨯=时，氧气瓶中，氧气的摩尔数为RTV P n 022,=所以能用的氧气摩尔数为()21021,P P RTV n n n -=-=∆ 平均每天用去氧气的摩尔数RTV P n 333,=故一瓶氧气能用的天数为()()5.91001.140.010113102.3,562332103=⨯⨯⨯-⨯=-=∆=-P V P P V n n N 1-3在湖面下50.0m 深处（温度为4.0C ），有一个体积为531.010m -⨯的空气泡升到湖面上来. 若湖面的温度为17.0C ，求气泡到达湖面的体积.（取大气压为50 1.01310Pa p =⨯）[解]：空气泡在湖面下50.0m 深处时，3511100.1,277m V K T -⨯==Pa P gh P 5530110013.610013.15010100.1⨯=⨯+⨯⨯⨯=+=ρ气泡到达湖面时，Pa P K T 522100.1,290⨯==由理想气体状态方程222111T V P T V P =得： 35351122121029.6100.12772900.1013.6m m V T T P P V --⨯=⨯⨯⨯=⋅=1-4如图所示，一定量的空气开始时在状态为A ，压力为2atm ，体积为l 2, 沿直线AB 变化到状态B 后，压力变为1 atm ，体积变为l 3. 求在此过程中气体所作的功。

大学物理2-1第九章(热力学基础)习题答案习 题 九9-1 一系统由图示的状态a 经acd 到达状态b ，系统吸收了320J 热量，系统对外作功126J 。

(1)若adb 过程系统对外作功 42J ，问有多少热量传入系统? (2)当系统由b 沿曲线ba 返回状态a ，外界对系统作功84 J ，试问系统是吸热还是放热? 热量是多少?[解] 由热力学第一定律A E Q +∆= 得AQ E -=∆在a <b 过程中，E E E a b∆=-JA Q 19412632011=-=-= 在adb 过程中 JA E Q 236421942=+=+∆=在ba 过程中 JA E A E E Q b a 27884194333-=--=+∆-=+-=本过程中系统放热。

9-2 2mol 氮气由温度为 300K ，压强为510013.1⨯Pa(1atm)的初态等温地压缩到 510026.2⨯Pa(2atm)。

求气体放出的热量。

[解] 在等温过程中气体吸收的热量等于气体对外做的功，所以J P P RT M m A Q mol T 3211046.321ln 30031.82ln ⨯-=⨯⨯⨯===即气体放热为J 31046.3⨯。

9-3 一定质量的理想气体的内能E 随体积的变化关系为E - V 图上的一条过原点的直线，如图所示。

试证此直线表示等压过程。

[证明] 设此直线斜率为k ，则此直线方程为kvE =又E 随温度的关系变化式为Tk T C M M E v mol'=⋅=所以T k kV '=因此C kk T V ='=(C 为恒量) 又由理想气体的状态方程知，C TpV '= (C '为恒量)所以 p 为恒量 即此过程为等压过程。

9-4 2mol 氧气由状态1变化到状态2所经历的过程如图所示：(1)沿l →m →2路径。

(2)1→2直线。

试分别求出两过程中氧气对外作的功、吸收的热量及内能的变化。

热学部分大练习一、填空题1. 相同温度下的1摩尔氧和2摩尔二氧化碳，对这两份气体，比较它们下列诸量的大小： （1）分子平均动能之比为_________________；（氧：二氧化碳） （2）分子平均平动动能之比为________________； （3）内能之比为____________________．2. 假设有一种气体，构成它的粒子服从以下速率分布率()()()⎩⎨⎧≥<<-=000 00)(v v v v v v Av v f式中A 为常量。

则用 v 0 定出的A =____________，平均速率=v __________________．3. 假设有N 个电子组成的电子气，其速率分布函数为f （v ）与v 的关系如图所示。

则A 的大小为________________，在速率0～900 m/s 间电子的平均速率为_____________。

4. 已知f (v )为麦克斯韦速率分布函数，N 为总分子数，则 (1) 速率v > 100 m ·s 1的分子数占总分子数的百分比的表达式为_________；(2) 速率v > 100 m ·s 1的分子数的表达式为__________________．5. 图示曲线为处于同一温度T 时氦(原子量4)、氖(原子量20)和氩(原子量40)三种气体分子的速率分布曲线。

其中 曲线 (a) 是 气体分子的速率分布曲线； 曲线 (c) 是 气体分子的速率分布曲线．6. 当理想气体处于平衡态时，若气体分子速率分布函数为f (v )，则分子速率处于最概然速率v p 至∞范围内的概率 △N / N ＝________________．7. 某理想气体，在温度T 1和T 2（T 1>T 2）时的麦克斯韦速率分布曲线如图所示，对应T 2的曲线应是__________，已知v 0是曲线Ⅱ的最可几速率，则曲线Ⅰ的最可几速率为____________。

第十六章习题16.8 氧气瓶的容积为32L ，其中氧气的压强为1.27⨯107P а，氧气厂规定压强降到9.8⨯105P а时，就应重新充气，以免经常洗瓶。

某小型吹玻璃车间，平均每天用400L ，1个工程大气压下的氧气，问一瓶氧气能用多少天？（设使用过程中，温度不变，1个工程大气压=9.8⨯104 P а）。

分析：由于使用条件的限制，瓶中氧气不能完全被使用，因此可通过两条不同的思路进行分析和求解； 解法（一）从氧气质量的角度来分析：设原瓶中氧气的总质量为1m ，需充气时瓶中剩余氧气的质量为2m ，每天使用氧气的质量为3m 。

由理想气体的状态方程MpV RT μ=可得：111p V m RT μ= ： 212p V m RT μ= 333p V m RT μ= 则一瓶氧气可用天数321)(m m m n -= 12133()p p V p V =-6.9≈天解法（二）从体积的角度来分析。

利用等温膨胀条件，将原瓶中氧气由初态，pa p 711027.1(⨯=，331323210V L m ==⨯) 膨胀到需充气条件下的终态，5229.810,p pa V =⨯待求），比较可得2p 状态下实际使用掉的氧气的体积为21V V -，同样将每天的氧气由初态41333(9.810,400410)p Pa V L m -=⨯==⨯等温压缩到压强为2p 的终态，并算出此的体积'2V ，由此可得使用天数为：212()n V V V '=-。

对等温膨胀过程利用理想气体的状态方程可得压强为pa p 52108.9⨯=时体积为 2112V p V p =每天使用相同状态的氧气的体积为 2332V p V p '= 可得瓶内氧气的可用天数为212n V V V '=- =12133()p p V p V - 5.9≈天16.9 水银气压计重混进了一个空气泡，因此它的读数比实际的气压要小一些。