基于MATLAB软件中SIMULINK的机构运动仿真

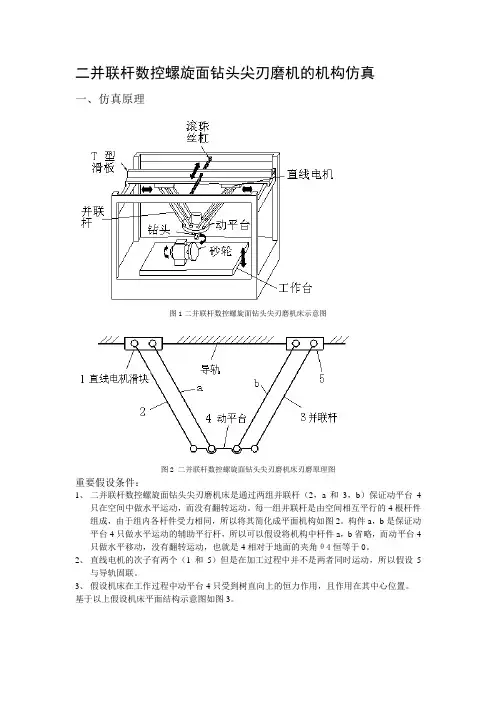
二并联杆数控螺旋面钻头尖刃磨机的机构仿真一、仿真原理图1二并联杆数控螺旋面钻头尖刃磨机床示意图图2 二并联杆数控螺旋面钻头尖刃磨机床刃磨原理图重要假设条件：1、二并联杆数控螺旋面钻头尖刃磨机床是通过两组并联杆（2，a和3，b）保证动平台4只在空间中做水平运动，而没有翻转运动。

每一组并联杆是由空间相互平行的4根杆件组成，由于组内各杆件受力相同，所以将其简化成平面机构如图2。

构件a，b是保证动平台4只做水平运动的辅助平行杆，所以可以假设将机构中杆件a，b省略，而动平台4只做水平移动，没有翻转运动，也就是4相对于地面的夹角θ4恒等于0。

2、直线电机的次子有两个（1和5）但是在加工过程中并不是两者同时运动，所以假设5与导轨固联。

3、假设机床在工作过程中动平台4只受到树直向上的恒力作用，且作用在其中心位置。

基于以上假设机床平面结构示意图如图3。

图3二并联杆数控螺旋面钻头尖刃磨机床简化机构平面结构示意图二、建立仿真方程C2=cos(θ2) S2=sin(θ2) C3=cos(θ3) S3=sin(θ3)一）力方程（分别对各个杆件进行受力分析）对动平台4：受力分析如图4F24x+F43x=m4*Ac4x （1）F24y+F43y=m4*Ac4y （2）F24y*rc4-F43y*rc4=0 （3）图4动平台4的受力分析对并联杆2：受力分析如图5F12x+F24x=-m2*Ac2x （4）F12y+F24y=-m2*Ac2y （5）F12x*rc2*S2+F12y*rc2*C2-F24x*rc2*S2-F24y*rc2*C2=I2*α2 （6）图5并联杆2的受力分析对直线电机滑块1：受力分析如图6Fm+F12x=m1*r1_dot_dot （7）Fy=F12y （8）图6直线电机滑块1的受力分析对并联杆3：受力分析如图7图7并联杆3的受力分析二）闭环矢量运动方程（矢量图如图8）图8 闭环矢量图矢量方程为：R1+R2=R3+R4将上述矢量方程分解为x和y方向，并分别对方程两边对时间t求两次导数得：r1_dot_dot+r2*α2*S2+r2*w2^2*C2=r3*α3*S3+r3*w3^2*C3 （12）r2*α2*C2-r2*w2^2*S2=r3*α3*C3-r3*w3^2*S3 （13）三）质心加速度的矢量方程F13x+F43x=-m3*Ac3x （9）F13y+F43y=-m3*Ac3y （10）F43x*r3*C3+F43y*r3*S3= I3*α3 （11）图9质心加速度的矢量示意图矢量关系：Ac3=Rc3_dot_dotAc4=R3_dot_dot+ Rc4_dot_dotAc2=R3_dot_dot+ R4_dot_dot+ Rc2_dot_dot (_dot_dot 表示对时间求两次导数)将上述三个矢量方程分别分解为x 和y 方向，则它们等效为以下六个方程；Ac3x=-rc3*w3^2*C3-rc3*α3*S3 (14) Ac3y=-rc3*w3^2*S3+rc3*α3*C3 (15) Ac4x=-r3*w3^2*C3-r3*α3*S3 (16) Ac4y=-r3*w3^2*S3+r3*α3*C3 (17) Ac2x=-r3*w3^2*C3-r3*α3*S3-rc2*w2^2*C2-rc2*α2*S2 (18) Ac2y=-r3*w3^2*S3+r3*α3*C3-rc2*w2^2*S2+rc2*α2*C2 (19) 力未知量为：F12x,F12y,F24x,F24y,F43x,F43y,F13x,F13y,Fy,Fm 引入的加速度有：α2，α3，r1_dot_dot ，Ac3x ，Ac3y ，Ac4x ，Ac4y ，Ac2x ，Ac2y三、系统方程的组装将所有19个方程组装成矩阵形式1010000000000200000010100000000002002222222200000020000000000101000000000000400001010000000000004000101000000000000010000000010010000000100000010000000000000010100000000m m rc S rc C rc S rc C I m m m ⋅⋅-⋅-⋅-----300000000101000000003000000333300003000000000000000002233100000000000000002233000000000000000002233010000000000000002233001000000000000000330001000000000000m m r C r S I r S r S r C r C rc S r S rc C r C rc S ⋅⋅-⋅-⋅⋅-⋅⋅⋅⋅⋅-⋅003300001000000000000033000001000000000000330001rc C r S r C ⎛⎫⎪ ⎪⎪⎪⎪ ⎪⎪⎪ ⎪⎪⎪ ⎪ ⎪ ⎪⎪⎪ ⎪⎪⎪ ⎪⎪⎪ ⎪⎪⎪⋅-⎪⋅ ⎪⎪ ⎪⋅-⎝⎭120120240240434301301300020333^2322^2222^2233^2322^222233441F x F y F x F y F x p F y F x F y Fy Fm r w C r w C r w S r w S rc w C Ac x Ac y Ac x Ac y Ac x Ac y r αα••⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⨯= ⎪ ⎪ ⎪⋅⋅-⋅⋅ ⎪ ⎪⋅⋅-⋅⋅ ⎪-⋅⋅ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭33^2322^2233^2333^2333^2333^2333^23r w S rc w S r w S rc w C rc w S r w C r w S ⎛⎫ ⎪⎪⎪ ⎪⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪⎪⎪ ⎪ ⎪ ⎪-⋅⋅ ⎪⋅⋅+⋅⋅ ⎪ ⎪-⋅⋅ ⎪ ⎪⋅⋅ ⎪-⋅⋅ ⎪⎪ ⎪⋅⋅⎝⎭ 四、初始条件的设定假设图3位置就是初始位置。

如何使用MATLABSimulink进行动态系统建模与仿真如何使用MATLAB Simulink进行动态系统建模与仿真一、引言MATLAB Simulink是一款强大的动态系统建模和仿真工具，广泛应用于各个领域的工程设计和研究中。

本文将介绍如何使用MATLAB Simulink进行动态系统建模与仿真的方法和步骤。

二、系统建模1. 模型构建在MATLAB Simulink中，可以通过拖拽模块的方式来构建系统模型。

首先，将系统的元件和子系统模块从库中拖拽到模型窗口中，然后连接这些模块，形成一个完整的系统模型。

2. 参数设置对于系统模型的各个组件，可以设置对应的参数和初始条件。

通过双击模块可以打开参数设置对话框，可以设置参数的数值、初始条件以及其他相关属性。

3. 信号连接在模型中，各个模块之间可以通过信号连接来传递信息。

在拖拽模块连接的同时，可以进行信号的名称设置，以便于后续仿真结果的分析和显示。

三、系统仿真1. 仿真参数设置在进行系统仿真之前，需要设置仿真的起止时间、步长等参数。

通过点击仿真器界面上的参数设置按钮，可以进行相关参数的设置。

2. 仿真运行在设置好仿真参数后，可以点击仿真器界面上的运行按钮来开始仿真过程。

仿真器将根据设置的参数对系统模型进行仿真计算，并输出仿真结果。

3. 仿真结果分析仿真结束后，可以通过查看仿真器界面上的仿真结果来分析系统的动态特性。

Simulink提供了丰富的结果显示和分析工具，可以对仿真结果进行绘图、数据处理等操作，以便于对系统模型的性能进行评估。

四、参数优化与系统设计1. 参数优化方法MATLAB Simulink还提供了多种参数优化算法，可以通过这些算法对系统模型进行优化。

可以通过设置优化目标和参数范围，以及定义参数约束条件等，来进行参数优化计算。

2. 系统设计方法Simulink还支持用于控制系统、信号处理系统和通信系统等领域的特定设计工具。

通过这些工具，可以对系统模型进行控制器设计、滤波器设计等操作，以满足系统性能要求。

[研究・设计]收稿日期:2007204209作者简介:赵小刚(1981-),男,陕西户县人,助教,主要研究方向为机械工程CAD CAM 。

MA TLAB S i m ulink 软件的曲柄导杆机构运动学仿真赵小刚1,李永春2 (1.陕西国防工业职业技术学院机械系,陕西户县　710302; 2.陕西科技大学机电工程学院,陕西西安　710021) 摘　要:为了求解曲柄导杆机构的运动学规律,运用矢量法进行了分析,建立了曲柄导杆机构的运动学数学模型。

使用M A TLAB Si m ulink 仿真软件对曲柄导杆机构进行了运动学仿真,得到了导杆及滑块的位移、速度、加速度的运动曲线。

使用这种方法求解机构的运动学参数具有精度高、速度快等特点。

关　键　词:曲柄导杆机构;运动学;M A TLAB Si m ulink 软件;仿真中图分类号:TH 112;T P 391.9 文献标志码:A 文章编号:100522895(2007)06200392030　引　言曲柄导杆机构是一种应用比较广泛的平面连杆机构,它可以将曲柄的旋转运动转换成为导杆的往复摆动(摆动导杆机构)或整周旋转运动(转动导杆机构)[1]。

曲柄导杆机构还可以与别的基本四杆机构组合在一起,构成一些实用的组合机构,如刨床,车床的主运动机构等。

机构的运动参数是分析评价机构工作性图1　曲柄摆动导杆机构简图能,优化新机构的基本依据[2]。

对曲柄导杆机构的运动分析,即构件上特定点的位移、速度和加速度分析,常用的方法有图解法和解析法。

图解法较直观、方便,但是精度不高,需要反复作图;而解析法人工计算运算量大,容易出错[3]。

本文以曲柄摆动导杆为例,提出用M A TLAB 软件仿真工具箱Si m u link 对曲柄导杆机构进行运动学仿真,得到曲柄导杆机构的运动曲线,该方法使解析法获得更高的精度。

1　曲柄摆动导杆机构运动学数学模型的建立图1所示为一曲柄摆动导杆机构,曲柄OA 为原动件,导杆B A 是从动件,通过滑块,曲柄的连续转动转变为导杆的往复摆动。

simulink建模及动态仿真的一些实验步骤Simulink是MATLAB中的一种可视化仿真工具，可以用于动态系统建模、仿真和分析。

以下是一些Simulink建模及动态仿真的实验步骤：启动Simulink：首先，需要打开MATLAB，然后在MATLAB 的命令窗口中输入“simulink”命令，或者点击工具栏中的Simulink 图标来启动Simulink。

新建模型：在Simulink的启动界面中，可以选择“Blank Model”来新建一个空白的模型。

也可以选择其他预设的模型模板来开始建模。

构建系统模型：在新建的模型窗口中，可以通过从Simulink 的模块库中拖拽模块到模型窗口中来构建系统模型。

模块库中包含了各种类型的模块，如源模块、接收模块、处理模块等。

将这些模块按照系统的结构和功能连接起来，形成一个完整的系统模型。

设置模块参数：对于模型中的每个模块，都可以双击打开其参数设置对话框，设置其参数和初始条件。

这些参数和初始条件将决定模块在仿真中的行为。

设置仿真参数：在模型窗口的工具栏中，可以点击“Simulation”->“Model Configuration Parameters”来打开仿真参数设置对话框。

在这个对话框中，可以设置仿真的起始和结束时间、仿真步长、求解器类型等参数。

开始仿真：完成以上步骤后，可以点击模型窗口工具栏中的“Run”按钮来开始仿真。

在仿真过程中，可以实时观察模型中各个模块的状态和输出。

分析结果：仿真结束后，可以使用Simulink提供的各种分析工具来分析仿真结果。

例如，可以使用示波器模块来显示仿真过程中某个模块的输出波形，也可以使用MATLAB的工作空间来查看和处理仿真数据。

以上步骤是一个基本的Simulink建模和动态仿真的过程。

在实际使用中，可能还需要根据具体的需求和系统特点进行一些额外的设置和调整。

基于MATLAB/Simulink的平面四连杆机构仿真一、题目及自由度分析如图1所示，该平面四杆机构中有三根运动的均质钢杆，其中有两根钢杆的一端与接地点连接，第三根杆就与这两根杆剩下的端点连接起来，两个接地点就可认为是第四杆，机构中相关尺寸如图2所示。

计算结构自由度，三个运动杆被限制到平面内运动，因此每个杆都有两个移动和一个转动，即在考虑约束之前，自由度为：3×(2+1)=9但是由于每个杆都受到约束，所以并不是每个自由度都是独立的。

在二维状态下，刚体间的连接或者刚体与接地点的连接就会增加两个约束。

这样就会使得刚体其中一端不能够作为独立的自由运动点，而是要受到邻近刚体的约束。

该题中有四个刚体--刚体或刚体—接地点的连接，这就隐含8个约束。

那么最后的自由度为9-8=1.虽然有四个转动自由度，但是，其中三个都是非独立的，只要确定其中一个，就可确定其余三个。

二、模型建立及参数设置1应用MATLAB/Simulink建立初始模型2在初始模型的基础上添加Joint Sensor模块3依题意设置相关参数⑴配置Ground模块由图2可得系统的基本尺寸为：①固定构件长86.7厘米②Ground_1表示接地点，在World CS坐标轴原点右边43.3cm处③Ground_2表示接地点，在World CS坐标轴原点左边43.4cm处④最下端的铰处于X-Z平面内原点以上4cm图5Ground_1模块参数设置图6Ground_2模块参数设置4配置Joint模块三个没有接地的联杆都是在X-Y平面内的，所以Revolute轴必须是Z轴。

⑴依次打开Revolute参数对话框，保持默认值，即Axis of rotation[x y z]默认设置为[001]，Reference csys都是WORLD。

图7Revolute坐标设置⑵根据连接情况依次设置Revolute参数对话框中的Connection parameters参数图8Revolute模块参数对话框Connection parameters参数图9Revolute模块参数对话框Connection parameters参数图10Revolute模块参数对话框Connection parameters参数图11Revolute模块参数对话框Connection parameters参数5配置Body模块本题中Body模块（即Bar）定位方式不是直接相对于WORLD坐标系统，而是采用相对坐标形式，Bar1的CS1相对于Ground_1，Bar2的CS1相对于Bar1，以此类推。

基于MATLAB/Simulink的平面四连杆机构仿真一、题目及自由度分析如图1所示，该平面四杆机构中有三根运动的均质钢杆，其中有两根钢杆的一端与接地点连接，第三根杆就与这两根杆剩下的端点连接起来，两个接地点就可认为是第四杆，机构中相关尺寸如图2所示。

计算结构自由度，三个运动杆被限制到平面内运动，因此每个杆都有两个移动和一个转动，即在考虑约束之前，自由度为：3×(2+1)=9但是由于每个杆都受到约束，所以并不是每个自由度都是独立的。

在二维状态下，刚体间的连接或者刚体与接地点的连接就会增加两个约束。

这样就会使得刚体其中一端不能够作为独立的自由运动点，而是要受到邻近刚体的约束。

该题中有四个刚体--刚体或刚体—接地点的连接，这就隐含8个约束。

那么最后的自由度为9-8=1.虽然有四个转动自由度，但是，其中三个都是非独立的，只要确定其中一个，就可确定其余三个。

二、模型建立及参数设置1应用MATLAB/Simulink建立初始模型2在初始模型的基础上添加Joint Sensor模块3依题意设置相关参数⑴配置Ground模块由图2可得系统的基本尺寸为：①固定构件长86.7厘米②Ground_1表示接地点，在World CS坐标轴原点右边43.3cm处③Ground_2表示接地点，在World CS坐标轴原点左边43.4cm处④最下端的铰处于X-Z平面内原点以上4cm图5Ground_1模块参数设置图6Ground_2模块参数设置4配置Joint模块三个没有接地的联杆都是在X-Y平面内的，所以Revolute轴必须是Z轴。

⑴依次打开Revolute参数对话框，保持默认值，即Axis of rotation[x y z]默认设置为[001]，Reference csys都是WORLD。

图7Revolute坐标设置⑵根据连接情况依次设置Revolute参数对话框中的Connection parameters参数图8Revolute模块参数对话框Connection parameters参数图9Revolute模块参数对话框Connection parameters参数图10Revolute模块参数对话框Connection parameters参数图11Revolute模块参数对话框Connection parameters参数5配置Body模块本题中Body模块（即Bar）定位方式不是直接相对于WORLD坐标系统，而是采用相对坐标形式，Bar1的CS1相对于Ground_1，Bar2的CS1相对于Bar1，以此类推。

基于MATLAB软件中SIMULINK的机构运动仿真
武娟;任家骏;吴凤林;刘群
【期刊名称】《机械工程与自动化》
【年(卷),期】2004(000)003
【摘要】给定机构的尺寸参数,列出所要分析机构加速度关系的闭环矢量方程,使用MATLAB软件中SIMULINK仿真工具可以方便地求出机构在所计时间域内连续运动中各个构件的瞬时位置、速度和加速度.作为一种运动分析的新方法,改变尺寸参数,可以方便地观察到机构运动特性的变化.使用这种方法分析了一种无级变速器机构.
【总页数】3页(P4-6)
【作者】武娟;任家骏;吴凤林;刘群
【作者单位】太原理工大学,机械工程学院,山西,太原,030024;太原理工大学,机械工程学院,山西,太原,030024;太原理工大学,机械工程学院,山西,太原,030024;太原第二热电厂,山西,太原,030041
【正文语种】中文
【中图分类】TB115
【相关文献】
1.基于Pro/E和Simulink正切机构擦鞋机的运动仿真 [J], 周欣;马兵
2.基于MATLAB软件对ULF车辆门架式转向架径向机构通过曲线的运动仿真分析[J], 张德乾;王伯铭;曹恺;李天一
3.基于Simulink的偏置摇杆滑块机构运动仿真分析 [J], 曾鹏; 李永平
4.基于Simulink的偏置摇杆滑块机构运动仿真分析 [J], 曾鹏;李永平
5.基于MATLAB/Simulink四轮转向机构的运动仿真与分析 [J], 严晟凯;黄博熠因版权原因，仅展示原文概要，查看原文内容请购买。