下载文档原格式
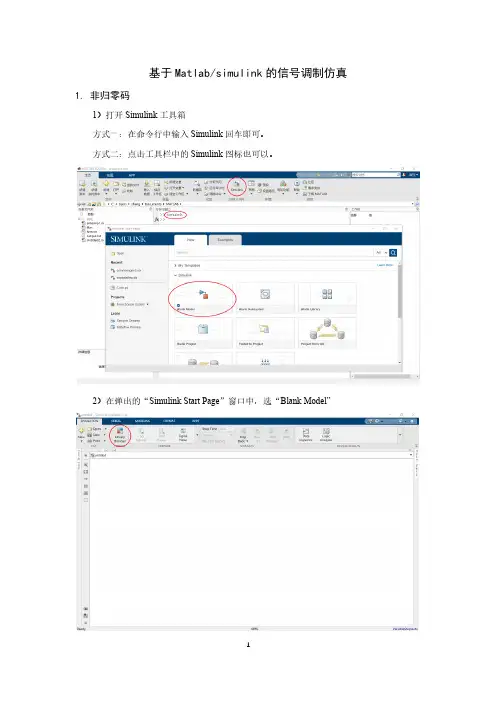
基于Matlab/simulink的信号调制仿真1.非归零码1）打开Simulink工具箱方式一：在命令行中输入Simulink回车即可。
方式二：点击工具栏中的Simulink图标也可以。
2）在弹出的“Simulink Start Page”窗口中，选“Blank Model”3）点击“Library Brower”，选Communications Toolbox ----> Comm Sources ----> Random Data Sources，将Random Integer Generator（随机整数发生器）模块拖入工作区。
双击Random Integer Generator，设置参数。
Set size 设为2，输出为0, 1两个值。
4）在“Library Brower”中，选Simulink ----> Signal Attributes，将Rate Transition（随机整数发生器）模块拖入工作区。
Rate Transition模块用于在不同采样率之间的转换。
双击Rate Transition模块进行参数设置。
提高输出采样率便于之后的频谱分析。
5）在“Library Brower”中，选Simulink ----> Sinks，将Scope（示波器）模块拖入工作区。
6）在“Library Brower”中，选DSP System Toolbox ----> Sinks，将Spectrum Analyzer（频谱分析仪）模块拖入工作区。
7）将各模板连接。
注意Stop Time的设置，必须满足有多于1024个采样点，否则无法进行傅里叶分析。
点击“Run”开始仿真。
8）双击Scope，观察时域波形。
9）双击Spectrum Analyzer，观察频谱。
点击左上角按纽，可进行设置。
点击工具，可放大/缩小、或平移图形。
2.数字调制1）ASK如下图。
各模块可在Simulink Library Browser中搜索得到。
一软件安装和破解
1.安装simlorer8软件，安装过程都为默认选择。
2.软件破解方法：破解文件夹下有下面三个文件：
1)复制license.lic文件到Ansoft\Admin文件夹下，替换原文件。
2)复制Ansoft2008Fix.exe文件到Ansoft\simplorer8folder，替换原文件，并运行。
3)复制simplorer8fix.exe文件到Ansoft\Simplorer8folder，替换原文件，并运行。
3.软件安装和破解完成，可以使用软件了。
二Simplore和Matlab的联合仿真实例
matlab_simplore文件夹为联合仿真的例子，文件夹下有三个文件：
1.仿真实例的路径名只能为英文，把matlab_simplore文件夹，拷贝到D盘或E 盘的根目录。
2.打开tosimulink文件，打开图1的，可以看到联合仿真的图形如图2。
图1图2
3.加载Simulink模块。
右击模块，打开一项，弹出如图3所示的对话框。
图3
4.点击，弹出4所示对话框。
图4
5.点击，弹出图5所示对话框。
图5
6.点击，选择sim2sim所在路径，并且给图6所示的两个复选框前选为。
图6
7.点击、、，回到simplore界面，点击图标，就可以运行了。
8.点击图1中的，可以查看仿真结果。
9.结束。
下面用一个简单的例子作介绍：（本例不是特别针对实现什么功能，只是为了介绍方便）第一部分创建一个模糊逻辑（.fis文件）第一步：打开模糊推理系统编辑器步骤：在Commond Window 键入fuzzy回车打开如下窗口，既模糊推理系统编辑器第二步：使用模糊推理系统编辑器本例用到两个输入，两个输出，但默认是一个输人，一个输出步骤：1、添加一个输入添加一个输出得如下图2、选择Input、output(选中为红框)，在Name框里修改各输入的名称并将And method 改为prod，将Or method 改为 probor提示：在命名时’_’在显示时为下标，可从上图看出。
第三步：使用隶属函数编辑器该编辑器提供一个友好的人机图形交互环境，用来设计和修改模糊推理系中各语言变量对应的隶属度函数的相关参数，如隶属度函数的形状、范围、论域大小等，系统提供的隶属度函数有三角、梯形、高斯形、钟形等，也可用户自行定义。
步骤：1、双击任何一个输入量（In_x、In_y）或输出量打开隶属度函数编辑器。
2、在左下处Range和Display Range处添加取值范围，本例中In_x和In_y的取值范围均为[0 10], Out_x和Out_y的取值范围均为[0 1]3、默认每个输入输出参数中都只有3个隶属度函数，本例中每个输入输出参数都需要用到五个，其余几个需要自己添加：选中其中一个输入输出参数点击Edit菜单，选Add MFS…打开下列对话框将MF type设置为trimf(三角形隶属度函数曲线，当然你也需要选择其他类型) 将Number of MFs 设置为2点击OK按钮同样给其他三个加入隶属度函数4、选中任何一个隶属度函数（选中为红色），在Name 中键入名称，在Type中选择形状，在Params中键入范围，然后回车如下图：5、关闭隶属函数编辑器第四步：使用规则编辑器通过隶规则编辑器来设计和修改“IF...THEN”形式的模糊控制规则。
如何使用MATLABSimulink进行动态系统建模与仿真如何使用MATLAB Simulink进行动态系统建模与仿真一、引言MATLAB Simulink是一款强大的动态系统建模和仿真工具，广泛应用于各个领域的工程设计和研究中。
本文将介绍如何使用MATLAB Simulink进行动态系统建模与仿真的方法和步骤。
二、系统建模1. 模型构建在MATLAB Simulink中，可以通过拖拽模块的方式来构建系统模型。
首先，将系统的元件和子系统模块从库中拖拽到模型窗口中，然后连接这些模块，形成一个完整的系统模型。
2. 参数设置对于系统模型的各个组件，可以设置对应的参数和初始条件。
通过双击模块可以打开参数设置对话框，可以设置参数的数值、初始条件以及其他相关属性。
3. 信号连接在模型中，各个模块之间可以通过信号连接来传递信息。
在拖拽模块连接的同时，可以进行信号的名称设置，以便于后续仿真结果的分析和显示。
三、系统仿真1. 仿真参数设置在进行系统仿真之前，需要设置仿真的起止时间、步长等参数。
通过点击仿真器界面上的参数设置按钮，可以进行相关参数的设置。
2. 仿真运行在设置好仿真参数后，可以点击仿真器界面上的运行按钮来开始仿真过程。
仿真器将根据设置的参数对系统模型进行仿真计算，并输出仿真结果。
3. 仿真结果分析仿真结束后，可以通过查看仿真器界面上的仿真结果来分析系统的动态特性。
Simulink提供了丰富的结果显示和分析工具，可以对仿真结果进行绘图、数据处理等操作，以便于对系统模型的性能进行评估。
四、参数优化与系统设计1. 参数优化方法MATLAB Simulink还提供了多种参数优化算法，可以通过这些算法对系统模型进行优化。
可以通过设置优化目标和参数范围，以及定义参数约束条件等，来进行参数优化计算。
2. 系统设计方法Simulink还支持用于控制系统、信号处理系统和通信系统等领域的特定设计工具。
通过这些工具，可以对系统模型进行控制器设计、滤波器设计等操作，以满足系统性能要求。
下面用一个简单的例子作介绍：（本例不是特别针对实现什么功能，只是为了介绍方便）第一部分创建一个模糊逻辑（.fis文件）第一步：打开模糊推理系统编辑器步骤：在Commond Window 键入fuzzy回车打开如下窗口，既模糊推理系统编辑器第二步：使用模糊推理系统编辑器本例用到两个输入，两个输出，但默认是一个输人，一个输出步骤：1、添加一个输入添加一个输出得如下图2、选择Input、output(选中为红框)，在Name框里修改各输入的名称并将And method 改为prod，将Or method 改为probor提示：在命名时’_’在显示时为下标，可从上图看出。
第三步：使用隶属函数编辑器该编辑器提供一个友好的人机图形交互环境，用来设计和修改模糊推理系中各语言变量对应的隶属度函数的相关参数，如隶属度函数的形状、范围、论域大小等，系统提供的隶属度函数有三角、梯形、高斯形、钟形等，也可用户自行定义。
步骤：1、双击任何一个输入量（In_x、In_y）或输出量打开隶属度函数编辑器。
2、在左下处Range和Display Range处添加取值范围，本例中In_x和In_y的取值范围均为[0 10], Out_x和Out_y的取值范围均为[0 1]3、默认每个输入输出参数中都只有3个隶属度函数，本例中每个输入输出参数都需要用到五个，其余几个需要自己添加：选中其中一个输入输出参数点击Edit菜单，选Add MFS…打开下列对话框将MF type设置为trimf(三角形隶属度函数曲线，当然你也需要选择其他类型) 将Number of MFs设置为2点击OK按钮同样给其他三个加入隶属度函数4、选中任何一个隶属度函数（选中为红色），在Name中键入名称，在Type 中选择形状，在Params中键入范围，然后回车如下图：5、关闭隶属函数编辑器第四步：使用规则编辑器通过隶规则编辑器来设计和修改“IF...THEN”形式的模糊控制规则。
MATLAB基础与应用简明教程张明等编著北京航空航天大学出版社(2001.01)MATLAB软件环境是美国New Mexico大学的Cleve Moler博士首创的，全名为MATrix LABoratory（矩阵实验室）。
它建立在20世纪七八十年代流行的LINPACK（线性代数计算）和ESPACK（特征值计算）软件包的基础上。
LINPACK和ESPACK软件包是从Fortran语言开始编写的，后来改写为C语言，改造过程中较为复杂，使用不便。
MA TLAB是随着Windows环境的发展而迅速发展起来的。
它充分利用了Windows环境下的交互性、多任务功能语言，使得矩阵计算、数值运算变得极为简单。
MA TLAB语言是一种更为抽象的高级计算机语言，既有与C语言等同的一面，又更为接近人的抽象思维，便于学习和编程。
同时，它具有很好的开放性，用户可以根据自己的需求，利用MA TLAB提供的基本工具，灵活地编制和开发自己的程序，开创新的应用。
本书重点介绍了MA TLAB的矩阵运算、符号运算、图形功能、控制系统分析与设计、SimuLink仿真等方面的内容。
Chap1 MATLAB入门与基本运算本章介绍MATLAB的基本概念，包括工作空间；目录、路径和文件的管理方式；帮助和例题演示功能等。
重点介绍矩阵、数组和函数的运算规则、命令形式，并列举了可能得到的结果。
由于MA TLAB的符号工具箱是一个重要分支，其强大的运算功能在科技领域有特殊的帮助作用。
1.1 MATLAB环境与文件管理1.2 工作空间与变量管理1.2.1 建立数据x1=[0.2 1.11 3]; y1=[1 2 3;4 5 6]建立一维数组x1和二维矩阵y1。
分号“；”表示不显示定义的数据。
MATLAB还提供了一些简洁方式，能有规律地产生数组：xx=1:10 %xx从1到10，间隔为1xx=-2:0.5:1 %xx从-2到1，间隔为0.5linespace命令等距离产生数组，logspace在对数空间中等距离产生数组。
MATLAB基础与应用简明教程张明等编著北京航空航天大学出版社(2001.01)MATLAB软件环境是美国New Mexico大学的Cleve Moler博士首创的，全名为MATrix LABoratory（矩阵实验室）。
它建立在20世纪七八十年代流行的LINPACK（线性代数计算）和ESPACK（特征值计算）软件包的基础上。
LINPACK和ESPACK软件包是从Fortran语言开始编写的，后来改写为C语言，改造过程中较为复杂，使用不便。
MA TLAB是随着Windows环境的发展而迅速发展起来的。
它充分利用了Windows环境下的交互性、多任务功能语言，使得矩阵计算、数值运算变得极为简单。
MA TLAB语言是一种更为抽象的高级计算机语言，既有与C语言等同的一面，又更为接近人的抽象思维，便于学习和编程。
同时，它具有很好的开放性，用户可以根据自己的需求，利用MA TLAB提供的基本工具，灵活地编制和开发自己的程序，开创新的应用。
本书重点介绍了MA TLAB的矩阵运算、符号运算、图形功能、控制系统分析与设计、SimuLink仿真等方面的内容。
Chap1 MATLAB入门与基本运算本章介绍MATLAB的基本概念，包括工作空间；目录、路径和文件的管理方式；帮助和例题演示功能等。
重点介绍矩阵、数组和函数的运算规则、命令形式，并列举了可能得到的结果。
由于MA TLAB的符号工具箱是一个重要分支，其强大的运算功能在科技领域有特殊的帮助作用。
1.1 MATLAB环境与文件管理1.2 工作空间与变量管理1.2.1 建立数据x1=[0.2 1.11 3]; y1=[1 2 3;4 5 6]建立一维数组x1和二维矩阵y1。
分号“；”表示不显示定义的数据。
MATLAB还提供了一些简洁方式，能有规律地产生数组：xx=1:10 %xx从1到10，间隔为1xx=-2:0.5:1 %xx从-2到1，间隔为0.5linespace命令等距离产生数组，logspace在对数空间中等距离产生数组。
对于这一类命令，只要给出数组的两端数据和维数就可以了。
xx=linespace(d1,d2,n) %表示xx从d1到d2等距离取n个点xx=logspace(d1,d2,n) %表明xx从10d1到10d2等距离取n个点1.2.2 who和whos命令who: 查看工作空间中有哪些变量名whos: 了解这些变量的具体细节1.2.3 exist命令查询当前的工作空间内是否存在一个变量，可以调用exist()函数来完成。
调用格式：i=exist(…A‟);式中，A为要查询的变量名。
返回的值i表示A存在的形式：i=1 表示当前工作空间内存在一个变量名为A的矩阵；i=2 表示存在一个名为A.m的文件；i=3 表示MATLAB的工作路径下存在一个名为A.mex的文件；i=4 表示存在一个编译好的名为A.mdl的SimuLink的文件；i=5 表示存在一个内部的MATLAB函数A()；i=0 表示不存在和A有关的变量和文件1.2.4 clear命令删除一些不再使用的变量。
变量之间用空格分开，不能加逗号。
1.2.5 format命令1.help命令help sqrt: 了解求平方根命令的功能和使用方式。
2 lookfor命令通过搜索所有MATLAB help标题，以及MATLAB搜索路径中M文件的第一行，返回包含所指定关键词的那些项。
Lookfor riccati: 得到所有解riccati方程的命令和解释语句3. 菜单驱动的帮助1.3 变量、数据与函数1.3.1 变量变量名必须是不含空格的单个词，其命名规则如下：变量名区分大小写；变量名最多不超过19个字符；必须以字母打头，之后可以是任意字母、数字或下划线。
标点符号在MATLAB中具有特殊含义，所以变量名中不允许使用标点符号。
1.3.2 注释和标点百分号后所有的文字为注释。
多条命令可以放在同一行，中间用逗号或分号隔开。
逗号要求显示结果，分号禁止显示结果。
1.3.3 复数表示用,i j 和()sqrt x （x 是任意整数、实数）表示。
复数和数学运算可以写成与实数相同的形式。
MATLAB 还可以用real,imag,abs,angle 命令来表示一个复数的实部、虚部、幅值和相角。
1.3.41.4 数据的输入与输出1.4.1 save和load命令(1) save: 以二进制格式将所有变量存入到matlab.mat文件中；(2) save data: 以二进制格式将所有变量存入到data.mat文件中；(3) save data x y z: 以二进制格式将变量x,y,z存入到data.mat文件中1.4.2 低级文件输入输出MATLAB提供了基于C语言的低级文件I/O命令，可以读写任意格式文件。
1.5 数组与矩阵运算由于数组可以定义为只有一行（或一列）的矩阵，因此，所有有关矩阵的运算可以用于数组运算。
1.5.1 矩阵表示与块操作1. 矩阵表达式MATLAB的数组与矩阵用[ ]表示，程序可以自行解读矩阵的行、列标志和元素。
定义矩阵的原则是：矩阵元素间用空格或逗号隔开，行用分号隔开。
如：a=[1 2 3;4 5 6],b=[7 8 9]2. 矩阵转置矩阵的转置（行、列互换）用'A表示。
若矩阵为复数矩阵，求转置时首先对矩阵元素进行转置，然后再逐项求取其共轭数值，这种转置方式双称为Hermit转置。
若x=[5.0000+1.0000i -2.0000+1.000i; 4.0000 +3.0000i]则xx=x‟=[5.0000-1.0000i 4.0000; -2.0000-1.0000i 0-3.0000i]3. 矩阵大小size: 格式为：[n,m]=size(A)。
n和m分别为A矩阵的行数与列数。
length: 格式为：n=length(A)。
n为A数组的元素个数或A矩阵的行、列数之最大值。
该函数等效于max(size(A))。
find命令：进行特殊要求的矩阵元素的定位。
如[i,j]=find(A>3)指出矩阵元素中大于3的元素的行、列位置。
4. 矩阵的块操作MATLAB提供了很多简便、智能的方式，可以对矩阵进行元素更改、插入子块、提取子块、重排子块、扩大维数等操作。
冒号“：”表示“全部”。
a(1,:)=b %将a的第1行中所有元素用b的元素替代。
a(:,:)=1 %将a的所有元素设为1。
a(2,3)=10 %第2行第3列元素等于10。
MATLAB已定义的矩阵的维数可以扩大，但不能缩小，除非利用clear命令删除该矩阵。
如果输入的同名矩阵的维数小于矩阵维数，MATLAB认为是原矩阵矩阵修改了部分元素或子块。
增加矩阵的维数时，可以只给出非零元素，MATLAB 自动将未定义元素设为0。
5. 矩阵的翻转操作矩阵上下翻转：flipud 命令将n 行矩阵作上下翻转，将A 的行按照n....1的顺序重新排列，A 的列保持不变。
如a=[1 2 3; 4 5 6; 7 8 9; 10 11 12]，则b=flipud(a)=[10 11 12; 7 8 9; 4 5 6; 1 2 3]矩阵左右翻转：fliplr 命令将m 列矩阵A 作左右翻转，将A 的列按照m...1的顺序重新排列，A 的行保持不变。
如c=fliplr(a)=[3 2 1; 6 5 4; 9 8 7; 12 11 10]矩阵逆时针90°旋转：如d=rot90(a)=[3 6 9 12; 2 5 8 11; 1 4 7 10]1.5.2 矩阵运算矩阵运算包括矩阵与标量、矩阵与矩阵的运算；矩阵函数和稀疏矩阵应用等。
1. 矩阵与标量的运算运算包括+、-、×、÷和乘方等运算。
矩阵与标量运算完成矩阵的每个元素对该标量的运算。
MATLAB 用符号“^”表示乘方。
求矩阵乘方时要求矩阵为方矩阵。
已知矩阵： b=[2 4; 1 5]，则b^2=[8 28; 7 29]（其平方为b×b ）；b^(-1)=[0.8333 -0.6667; -0.1667, 0.3333]（实际是求b 的逆矩阵）p=b^(0.2)=[1.0862 0.3448; 0.0862 1.3448]（将b 矩阵开5次方，即b=p 5） 2. 矩阵与矩阵的运算矩阵加减法运算：矩阵A 和B 的维数完全相同时，可以进行矩阵加减法运算。
它会自动地使得A 和B 矩阵的相应元素相加减。
如果A 和B 维数不相等，则给出错误信息。
矩阵乘法运算：两个矩阵A,B 的维数相容时（A 的列数等于B 的行数），可以进行C=A×B 的运算矩阵除法运算：包括左除和右除两种，其中： 左除：A\B=A -1B ，A 为方矩阵 右除：A/B=AB -1，B 为方矩阵矩阵的除法运算实际上是求AX=B 的解的过程。
当A 为非奇异矩阵时，结果是最小二乘解，即矩阵除法可找到使AX B -误差绝对值最小的X 。
矩阵的点运算：两个矩阵之间的点运算是该矩阵对应元素的直接运算，如C=A. ×B 表示A 和B 矩阵的相应元素之间直接进行乘法运算，然后将结果赋给C 。
点乘积运算要求A 和B 的维数相同。
这种点乘积又称为Hadamard 乘积。
矩阵求幂：包括矩阵与常数和矩阵与矩阵的幂运算。
3.^3[]ij a a =: a 矩阵的3次方—A 矩阵的每个元素的3次方形成的新矩阵；3.^[3]ij aa =: 3的a 次方—新矩阵的每个元素都是以3为底，以A 矩阵的对应元素为幂指数，形成的新矩阵； .^[]ijb ija b a =: a 的b 次方—新矩阵的每个元素都以A 的元素为底，以B 的对应元素为幂指数。
1.5.3 矩阵函数MATLAB 定义了一些特殊矩阵，不必一一赋值。
特殊矩阵定义见下表：MATLAB 还提供了很多用于求解线性代数数值问题的矩阵函数，见下表：1.5.4 稀疏矩阵稀疏矩阵是一个阶数很高，只有极小部分元素非零的矩阵。
a=speye(5) %建立5阶单位稀疏矩阵sparse(i,j,s)命令可以产生最大行数为i ，最大列数为j ，最后一个元素为s 的稀疏矩阵。
aa=sparse(10,10,1) %建立10×10阶稀疏矩阵，最后一个元素为1 ap=sparse(1:5,6,0.5) %建立5×6稀疏矩阵，第6列元素为0.5 as=sparse(1:5,1:5,0.5) %建立5×5稀疏矩阵，对角线元素为0.5 1.6 M 函数与M 文件全局变量：global a b c 1.7 多项式运算多项式用一个向量表示，多项式的系数降幂排列。
如多项式43()256p x x x x =+-+在MATLAB 工作空间输入为：p=[1 2 0 -5 6] 1.7.1 求根及其求逆运算roots 命令可以求解多项式p 的根，求出的根按列向量存储，如rr=roots(p)。
