【配套K12】[学习]河北省石家庄市2019年中考数学总复习 第六章 圆 第三节 与切线有关的证明与

单元测试(六)范围:圆限时:60分钟满分:100分一、选择题(每小题5分,共45分)1.如图D6-1,☉O的半径为5,AB为弦,半径OC⊥AB,垂足为E,若OE=3,则AB的长是()图D6-1A.4B.6C.8D.10⏜的度数别为88°,32°,则∠P的度数为⏜,AA2.如图D6-2,P是☉O外一点,PA,PB分别交☉O于C,D两点,已知AA()图D6-2A.26°B.28°C.30°D.32°3.某数学研究性学习小组制作了如图D6-3所示的三角函数计算图尺:在半径为1的半圆形量角器中,画一个直径为1的圆,把刻度尺CA的0刻度固定在半圆的圆心O处,刻度尺可以绕点O旋转.从图中所示的图尺可读出sin∠AOB的值是()图D6-3A.58 B.78C.710D.454.如图D6-4,四边形ABCD内接于☉O,已知∠ADC=130°,则∠AOC的度数是()图D6-4A.80°B.100°C.60°D.40°5.如图D6-5,在平面直角坐标系xOy中,已知点A(0,3),点B(2,1),点C(2,-3),则经画图操作可知△ABC的外心坐标应是()图D6-5A.(0,0)B.(1,0)C.(-2,-1)D.(2,0)6.在△ABC中,∠C=90°,AC=4,AB=5,以点C为圆心,R为半径画圆,若☉C与边AB只有一个公共点,则R的取值范围是()A.R=125B.3≤R≤4C.0<R<3或R>4D.3<R≤4或R=1257.将直径为60 cm的圆形铁皮,做成三个相同的圆锥容器的侧面(不浪费材料,不计接缝处的材料损耗),那么每个圆锥容器的底面半径为()A.10 cmB.30 cmC.45 cmD.300 cm8.如图D6-6,半径为1的☉O与正五边形ABCDE相切于点A,C,劣弧AC的长度为()图D6-6A .35πB .45πC .34πD .23π9.如图D6-7,正六边形螺帽的边长是2 cm,这个扳手的开口a 的值应是 ( )图D6-7A .2√3 cmB .√3 cmC .2√33cm D .1 cm二、 填空题(每小题5分,共20分)10.已知圆柱的侧面积是20π cm 2,高为5 cm,则圆柱的底面圆半径为 .11.如图D6-8,☉O 与AB 相切于点A ,BO 与☉O 交于点C ,∠BAC=24°,则∠B 等于 .图D6-812.如图D6-9,AB 是☉O 的直径,点E 为BC 的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和是 .图D6-913.如图D6-10,直线l 与x 轴,y 轴分别相交于A ,B 两点,已知B (0,√3),∠BAO=30°,圆心P 的坐标为(1,0).☉P 与y 轴相切于点O,若将☉P沿x轴向左移动,当☉P与直线l相交时,点P的横坐标为整数的个数是.图D6-10三、解答题(共35分)14.(10分)如图D6-11,AB是半圆的直径,O是圆心,C是半圆上一点,D是AA⏜中点,OD交弦AC于E,连接BE,若AC=8,DE=2,求:图D6-11(1)半圆的半径长;(2)BE的长度.⏜的中点,作DE⊥AC,交AB的延长线于点F,连接15.(12分)如图D6-12,AB为半圆O的直径,AC是☉O的一条弦,D为AADA.(1)求证:EF为半圆O的切线;(2)若DA=DF=6√3,求阴影部分的面积.(结果保留根号和π)图D6-1216.(13分)如图D6-13,菱形ABCD中,对角线AC,BD相交于点O,AC=12 cm,BD=16 cm,动点N从点D出发,沿线段DB以2 cm/s 的速度向点B运动,同时动点M从点B出发,沿线段BA以1 cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也随之停止.设运动时间为t(s)(t>0).以点M为圆心,MB的长为半径的☉M与射线BA,线段BD分别交于点E,F,连接EN.图D6-13(1)求BF的长(用含有t的代数式表示),并求出t的取值范围.(2)当t为何值时,线段EN与☉M相切?(3)若☉M与线段EN只有一个公共点,求t的取值范围.参考答案1.C2.B [解析] 由题意,知AA ⏜,AA ⏜所对的圆心角的度数分别为88°和32°,∴∠A=12×32°=16°,∠ADB=12×88°=44°.∵∠P+∠A=∠ADB ,∴∠P=∠ADB-∠A=44°-16°=28°.3.D [解析] 如图,连接AD.∵OD 是直径,∴∠OAD=90°,∵∠AOB+∠AOD=90°,∠AOD+∠ADO=90°,∴∠AOB=∠ADO ,∴sin ∠AOB=sin ∠ADO=810=45,故选D .4.B [解析] ∵四边形ABCD 内接于☉O ,∠ADC=130°,∴∠B=180°-130°=50°. 由圆周角定理,得∠AOC=2∠B=100°.故选B .5.C [解析] △ABC 的外心即三角形三边垂直平分线的交点,由此可作图如下:EF 与MN 的交点O'即为所求的△ABC 的外心,∴△ABC 的外心坐标是(-2,-1).6.D [解析] 过点C 作CD ⊥AB 于点D ,由题意,知AC=4,BC=3,AB=5.当边AB 与☉C 相切时,☉C 与斜边AB 只有一个公共点,由CD ·AB=AC ·BC ,可得CD=R=125;如图所示,当3<R ≤4时,☉C 与斜边AB 也只有一个公共点.故R 的取值范围为3<R ≤4或R=125.7.A [解析] 根据将直径为60 cm 的圆形铁皮,做成三个相同的圆锥容器的侧面(不浪费材料,不计接缝处的材料损耗),得直径为60 cm 的圆形铁皮被分成三个圆心角是120°,半径为30 cm 的扇形,假设每个圆锥容器的底面半径为r ,∴120×π×30180=2πr ,解得r=10(cm).故选A .8.B [解析] 正五边形ABCDE 的内角和是(5-2)×180°=540°,其每一个内角的度数为540°÷5=108°.连接OA ,OB ,OC ,∵☉O 与正五边形ABCDE 相切于点A ,C , ∴∠OAE=∠OCD=90°,∴∠OAB=∠OCB=108°-90°=18°, ∴∠AOC=144°. ∴劣弧AC 的长度为144π×1180=45π.9.A [解析] 连接AC ,作BD ⊥AC 于点D.根据正六边形的特点求出∠ABC 的度数,再由等腰三角形的性质求出∠BAD 的度数,由特殊角的三角函数值求出AD 的长,进而可求出AC 的长.10.2 cm11.42° [解析] 连接OA ,则OA ⊥AB.∵∠BAC=24°,∴∠OAC=90°-24°=66°. ∵OA=OC ,∴∠OCA=∠OAC=66°, ∴∠B=66°-24°=42°.12.√3 [解析] 首先证明△ABC 是等边三角形,则△EDC 是等边三角形,边长是2.通过观察,可知AA ⏜和弦BE 围成的部分的面积=AA ⏜和弦DE 围成的部分的面积,据此即可求解. 13.3个 [解析] 如图,作☉P'与☉P″分别切AB 于D ,E.∵B(0,√3),∠BAO=30°,∴OA=AA=3,则A点坐标为(-3,0).连接P'D,P″E,则P'D⊥AB,P″E⊥AB,则在Rt△ADP'tan30°中,AP'=2×DP'=2,同理可得,AP″=2,则P'的横坐标为-3+2=-1,P″的横坐标为-3-2=-5,∴P的横坐标x的取值范围为-5<x<-1,∴横坐标为整数的点P坐标为(-2,0),(-3,0),(-4,0),共3个.14.解:(1)设半圆的半径为r,AC=4,∵D是AA⏜中点,∴OD⊥AC,AE=EC=12在Rt△AOE中,OA2=OE2+AE2,即r2=(r-2)2+42,解得,r=5,即半圆的半径长为5.(2)连接BC,由(1)知OE=3,∵AO=OB,AE=EC,∴BC=2OE=6,∵AB是半圆的直径,∴∠ACB=90°,∴BE=√AA2+AA2=2√13.⏜的中点,∴∠CAD=∠BAD.15.解:(1)证明:连接OD,∵D为AA∵OA=OD,∴∠BAD=∠ADO.∴∠CAD=∠ADO.∵DE⊥AC,∴∠E=90°.∴∠CAD+∠EDA=90°,即∠ADO+∠EDA=90°.∴OD⊥EF.∴EF为半圆O的切线.(2)连接OC ,CD.∵DA=DF ,∴∠BAD=∠F ,∴∠BAD=∠F=∠CAD.又∵∠BAD+∠CAD+∠F=90°,∴∠F=30°,∠BAC=60°. ∵OC=OA ,∴△AOC 为等边三角形. ∴∠AOC=60°,∠COB=120°. ∵OD ⊥EF ,∠F=30°,∴∠DOF=60°.在Rt △ODF 中,DF=6√3,∴OD=DF ·tan30°=6.在Rt △AED 中,DA=6√3,∠CAD=30°,∴DE=DA ·sin30°=3√3,EA=DA ·cos30°=9.∵∠COD=180°―∠AOC ―∠DOF=60°,由CO=DO 得△COD 为等边三角形,∴∠OCD=60°,∴∠AOC=∠OCD , ∴CD ∥AB.故S △ACD =S △COD .∴S 阴影=S △AED -S 扇形COD =12×9×3√3-60360×π×62=27√32-6π.16.解:(1)如图①所示,连接EF.∵四边形ABCD 为菱形,AC=12 cm,BD=16 cm, ∴AC ⊥BD ,OA=6 cm,OB=8 cm, ∴AB=√2+2=10(cm), ∴cos ∠ABO=45. ∵BE 为☉M 的直径, ∴∠EFB=90°,∴BF=BE ·cos∠ABO=2t ·45=85t.∵101=10 s,162=8 s,∴t 的取值范围为0<t ≤8.(2)如图②所示,∵EN 为☉M 的切线,∴BE ⊥EN ,∴cos ∠ABO=AA AA =45.又∵BN=BD-ND=(16-2t )cm,BE=2t cm, ∴2A 16-2A =45,解得t=329.∴当t=329 时,线段EN 与☉M 相切.(3)如图③所示,在EN 与☉M 相切或相切前,EN 与☉M 只有一个公共点. 由(2)可知此时0<t ≤329.如图④所示,当点N 与点F 重合时,EN 与☉M 恰好有两个公共点.∵BF=BD-DN ,∴85t=16-2t ,解得t=409.当点N 位于点F 的左侧时,EN 与☉M 只有一个公共点, ∴409<t<8.综上所述,当0<t ≤329或409<t<8时,☉M 与线段EN 只有一个公共点.。

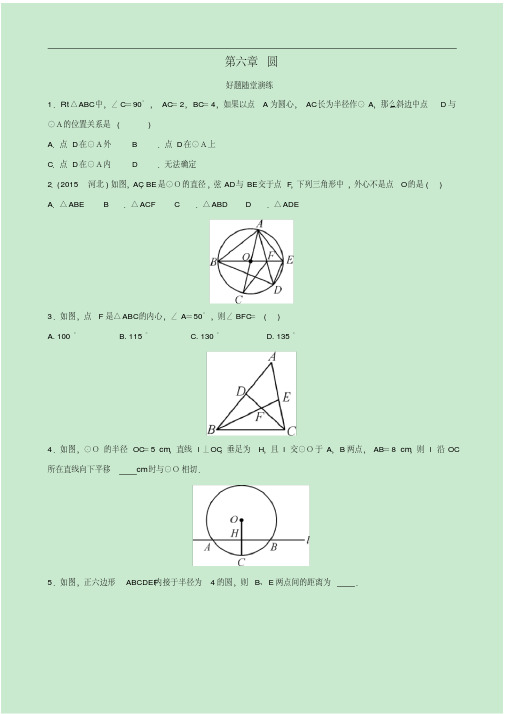
第六章圆好题随堂演练1．Rt△ABC中，∠C＝90°，AC＝2，BC＝4，如果以点A为圆心，AC长为半径作⊙A，那么斜边中点D与⊙Ａ的位置关系是( )A．点D在⊙Ａ外 B．点D在⊙Ａ上C．点D在⊙Ａ内 D．无法确定2．(2015·河北)如图，AC，BE是⊙Ｏ的直径，弦AD与BE交于点F，下列三角形中，外心不是点O的是( ) A．△ABE B．△ACF C．△ABD D．△ADE3．如图，点F是△ABC的内心，∠A＝50°，则∠BFC＝( )A. 100°B. 115°C. 130°D. 135°4．如图，⊙Ｏ的半径OC＝5 cm，直线l⊥OC，垂足为H，且l交⊙Ｏ于A，B两点，AB＝8 cm，则l沿OC 所在直线向下平移cm时与⊙Ｏ相切．5．如图，正六边形ABCDEF内接于半径为4的圆，则B、E两点间的距离为．6．(2017·宜宾)如图，⊙Ｏ的内接正五边形ABCDE 的对角线AD 与BE 相交于点G ，AE ＝2，则EG 的长是．7．如图，正方形ABCD 内接于⊙O ，M 为AD ︵的中点，连接BM ，CM.(1)求证：BM ＝CM ；(2)当⊙Ｏ的半径为2时，求∠BOM 的度数．参考答案1．A 2.B 3.B 4.2 5.8 6.5－17．(1)证明：∵四边形ABCD 是正方形，∴AB ＝CD ，∴AB ︵＝CD ︵，∵Ｍ为AD ︵的中点，∴AM ︵＝DM ︵，∴AB ︵＋AM ︵＝CD ︵＋DM ︵，即BM ︵＝CM ︵，∴BM ＝CM ；(2)解：如解图，连接OM ，OB ，OC ，∵BM ︵＝CM ︵，∴∠BOM ＝∠COM ，∵正方形ABCD 内接于⊙O ，∴∠BOC ＝360°4＝90°，∴∠BOM ＝12×(360°－90°)＝135°.。

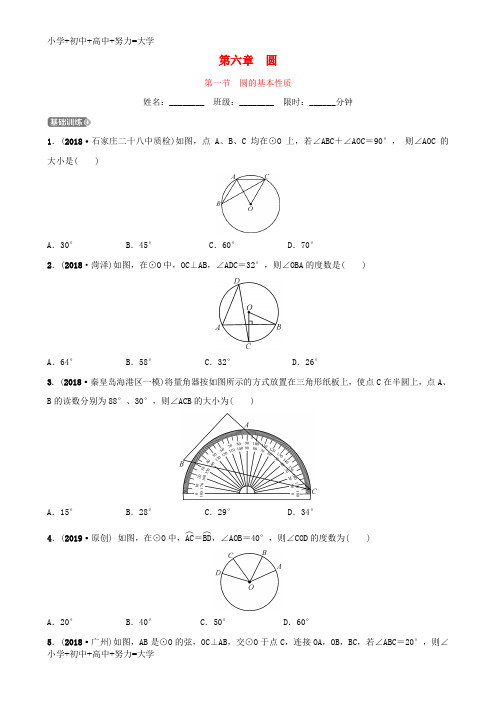
第六章 圆第一节 圆的基本性质姓名：________ 班级：________ 限时：______分钟1．(2018·石家庄二十八中质检)如图，点 A 、B 、C 均在⊙O 上，若∠ABC＋∠AOC＝90°， 则∠AOC 的大小是( )A ．30°B ．45°C ．60°D ．70°2．(2018·菏泽)如图，在⊙O 中，OC⊥AB，∠ADC＝32°，则∠OBA 的度数是( )A ．64°B ．58°C ．32°D ．26°3．(2018·秦皇岛海港区一模)将量角器按如图所示的方式放置在三角形纸板上，使点C 在半圆上，点A 、B 的读数分别为88°、30°，则∠ACB 的大小为( )A ．15°B ．28°C ．29°D ．34°4．(2019·原创) 如图，在⊙O 中，AC ︵＝BD ︵，∠AOB ＝40°，则∠COD 的度数为( )A ．20°B ．40°C ．50°D ．60°5．(2018·广州)如图，AB 是⊙O 的弦，OC⊥AB，交⊙O 于点C ，连接OA ，OB ，BC ，若∠ABC＝20°，则∠AOB的度数是( )A．40° B．50° C．70° D．80°6．(2018·聊城)如图，⊙O 中，弦BC与半径OA相交于点D，连接AB，OC.若∠A＝60°，∠ADC＝85°，则∠C的度数是( )A．25° B．27.5° C．30° D．35°7．(2019·原创)如图，在半径为4的⊙O中，弦AB∥OC，∠BOC＝30°，则AB的长为( )A．2 B．2 3 C．4 D．4 38．(2018·陕西改编)如图，△ABC的顶点A，B，C均在⊙O上，AB＝AC，∠BCA＝65°，作CD∥AB，并与⊙O相交于点D，连接BD，则∠DBC的大小为( )A．15° B．25° C．35° D．45°9．(2018·甘肃省卷)如图，⊙A过点O(0，0)，C(3，0)，D(0，1)，点B是x轴下方⊙A上的一点，连接BO，BD，则∠OBD的度数是( )A ．15°B ．30°C ．45°D ．60°10．(2018·张家口桥东区模拟)如图，半径为5的⊙A 中，弦BC ，ED 所对的圆心角分别是∠BAC，∠EAD，若DE ＝6，∠BAC＋∠EAD＝180°，则弦BC 的长等于( )A ．8B ．10C ．11D ．1211．(2018·保定二模)“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”将其抽象为数学问题大致如下：如图所示，CD 垂直平分弦AB ，CD ＝1寸，AB ＝1尺，求圆的直径．(1尺＝10寸)，根据题意可知直径长为( )A ．10寸B ．20寸C ．13寸D ．26寸12．(2018·泰安)如图，⊙O 是△ABC 的外接圆，∠A＝45°，BC ＝4，则⊙O 的直径为________．13．(2018·无锡)如图，点A 、B 、C 都在⊙O 上，OC⊥OB，点A 在劣弧BC ︵上，且OA ＝AB ，则∠ABC＝________．14．(2019·原创)如图，等腰△ABC 内接于⊙O，已知AB ＝AC ，∠ABC＝30°，BD 是⊙O 的直径，如果CD＝433，则AD ＝________．15．(2018·杭州)如图，AB 是⊙O 的直径，点C 是半径OA 的中点，过点C 作DE⊥AB，交⊙O 于D 、E 两点，过点D 作直径DF ，连接AF ，则∠DFA＝________． 16．(2019·原创)如图，AB 是⊙O 的直径，CD 是⊙O 的弦，且CD⊥AB 于点E. (1)求证：∠BCO＝∠D；(2)若CD ＝8，AE ＝3，求⊙O 的半径r.1．(2017·广安)如图，AB 是⊙O 的直径，且经过弦CD 的中点H ，已知cos ∠C DB ＝45，BD ＝5，则OH 的长度为( )A.23B.56 C ．1 D.762．(2018·河北第7次联考)如图，点D 、E 分别是⊙O 的内接正三角形ABC 的AB 、AC 边上的中点，若⊙O 的半径为2，则DE 的长等于( )A. 3B. 2 C ．1 D.323．(2019·原创)如图，△ABC 是等腰直角三角形，其中AB ＝AC ，∠BAC＝90°，⊙O 经过点B ，C ，连接OA ，若AO ＝1，BC ＝6，则⊙O 的半径为________．4．(2019·原创)如图，已知△ABC 内接于⊙O，AB 是直径，点D 在⊙O 上，OD∥BC，过点D 作DE⊥AB，垂足为E ，连接CD 交OE 于点F. (1)求证：△DOE∽△ABC；(2)连接OC ，设△DOE 的面积为S 1，四边形BCOD 的面积为S 2，若S 1S 2＝27，求sin A 的值．参考答案【基础训练】1．C 2.D 3.C 4.B 5.D 6.D 7.D 8.A 9.B 10.A 11．D 12.4 2 13.15° 14.4 15.30° 16．(1)证明：∵OB＝OC ，∴∠OBC＝∠OCB， ∵∠ADC＝∠ABC，∴∠BCO＝∠D ；(2)解：∵OA⊥CD，∴CE＝DE ＝4，设⊙O 的半径为r ，则OE ＝OA －AE ＝r －3，在Rt △OCE 中，由勾股定理得OC 2＝CE 2＋OE 2，即r 2＝42＋(r －3)2，解得r ＝256.【拔高训练】 1．D 2.A 3.134．(1)证明：∵AB 是⊙O 的直径，∴∠ACB＝90°， ∵DE⊥AB，∴∠DEO＝90°， ∴∠DEO＝∠ACB，∵OD∥BC，∴∠DOB＝∠ABC， ∴△DOE∽△ABC.(2)解：∵△DOE∽△ABC，∴S △DOE S △ABC ＝(DO AB )2＝14，∴S △ABC ＝4S △DOE ＝4S 1，∵OA＝OB ，∴S △BOC ＝12S △ABC ＝2S 1，∵S 四边形BCOD ＝S △BCO ＋S △DOE ＋S △BDE ，S 1S 2＝27，∴S 1S 1＋2S 1＋S △DBE ＝27，解得S △DBE ＝S 12，∴S △ODE ＝2S △DBE ， ∴OE＝2BE ，∴OD＝32OE ，∴sin A ＝sin ∠ODE＝OE OD ＝23.。

第六单元 圆命题点1 垂径定理1．(2012·河北T5·2分)如图，CD 是⊙O 的直径，AB 是弦(不是直径)，AB ⊥CD 于点E ，则下列结论正确的是(D)A ．AE>BEB.AD︵＝BC ︵ C ．∠D ＝12∠AECD ．△ADE ∽△CBE命题点2 圆周角定理2．(2011·河北T16·3分)如图，点O 为优弧AB ︵所在圆的圆心，∠AOC ＝108°，点D 在AB 的延长线上，BD ＝BC ，则∠D ＝27°．重难点1 垂径定理及其应用已知AB 是半径为5的⊙O 的直径，E 是AB 上一点，且BE ＝2. (1)如图1，过点E 作直线CD⊥AB，交⊙O 于C ，D 两点，则CD ＝8；图1 图2 图3 图4探究：如图2，连接AD ，过点O 作OF⊥AD 于点F ，则OF(2)过点E 作直线CD 交⊙O 于C ，D 两点．①若∠AED＝30°，如图3，则CD ②若∠AED＝45°，如图4，则CD【思路点拨】 由于CD 是⊙O 的弦，因此利用圆心到弦的距离(有时需先作弦心距)，再利用垂径定理，结合勾股定理，求出弦的一半，再求弦．【变式训练1】 (2018·襄阳)如图，点A ，B ，C ，D 都在半径为2的⊙O 上．若OA⊥BC，∠CDA＝30°，则弦BC 的长为(D )A ．【变式训练2】 AB ＝16 cm ，CD ＝方法指导123．事实上，重难点2(1)如图1(2)如图2①求BC ②若点C 是(3)如图3图1 图2 图3【思路点拨】 连接OB ，OC ，利用同弧所对的圆心角等于圆周角的2倍，构建可解的等腰三角形求解． 【自主解答】 解：(1)连接OB ，OC.∵∠BOC＝2∠A＝60°，OB ＝OC ，∴△OBC 是等边三角形． ∴BC＝OB ＝4.(2)①连接OB ，OC.∵∠BOC＝2∠A＝90°，OB ＝OC ，∴△OBC 是等腰直角三角形． ∵OB＝OC ＝4，∴BC＝4 2.②∵点C 是AB ︵的中点，∴∠ABC＝∠A＝45°. ∴∠ACB＝90°.∴AB 是⊙O 的直径．∴AB＝8.(3)在优弧BC ︵上任取一点D ，连接BD ，CD ，连接BO ，CO. ∵∠A＝135°，∴∠D＝45°.∴∠BOC＝2∠D＝90°.∵OB ＝OC ＝4，∴BC＝4 2.【变式训练3】 (2018·南充)如图，BC 是⊙O 的直径，A 是⊙O 上的一点，∠OAC＝32°，则∠B 的度数是(A )A ．58°B ．60°C ．64°D ．68°【变式训练4】 (2018·秦皇岛海港区一模)将量角器按如图所示的方式放置在三角形纸板上，使点C 在半圆上．点A ，B 的读数分别为88°，30°，则∠ACB 的大小为(C )A ．15°B ．28°C ．29°D ．34°方法指导1．在圆中由已知角求未知角，同(等)弧所对的圆心角和圆周角的关系是一个重要途径，其关键是找到同一条弧．2．弦的求解可以通过连接圆心与弦的两个端点，构建等腰三角形来解决． 3．一条弦所对的两种圆周角互补，即圆内接四边形的对角互补．模型建立在半径已知的圆内接三角形中，若已知三角形一内角，可以求得此角所对的边． 易错提示注意同弧所对的圆心角是圆周角的2倍，避免把数量关系弄颠倒．重难点3 圆内接四边形(2017·潍坊)如图，四边形ABCD 为⊙O 的内接四边形．延长AB 与DC 相交于点G ，AO⊥CD，垂足为E ，连接BD ，∠GBC＝50°，则∠DBC 的度数为(C )A ．50°B ．60°C ．80°D ．90°【思路点拨】 延长AE 交⊙O 于点M ，由垂径定理可得CD ︵＝2DM ︵，所以∠CBD＝2∠EAD.由圆内接四边形的对角互补，可推得∠ADE＝∠GBC，而∠ADE 与∠EAD 互余，由此得解．【变式训练5】 (2018·邵阳)如图所示，四边形ABCD 为⊙O 的内接四边形，∠BCD＝120°，则∠BOD 的大小是(B )A．80° B．120° C．100° D．90°【变式训练6】(2018·曲靖)如图，四边形ABCD内接于⊙O，E为BC延长线上一点．若∠A＝n°，则∠DCE＝n°方法指导1．找圆内角外)2．Ｋ1．如图，在⊙OA．AB＝AC2中，弦AB∥OC，∠BOC＝30°，则A． 3 C．4 D3．(2017·承德模拟)如图，在平面直角坐标系中，⊙O′经过原点O，并且分别与x轴、y轴交于点B，C，分别作O′E⊥OC于点E，O′D⊥OB于点D.若OB＝8，OC＝6，则⊙O′的半径为(C)A．7 B．6 C．5 D．44．(2018·聊城)如图，在⊙O中，弦BC与半径OA相交于点D，连接AB，OC.若∠A＝60°，∠ADC＝85°，则∠C 的度数是(D)A．25° B．27.5° C．30° D．35°5．(2018·陕西)如图，△ABC是⊙O的内接三角形，AB＝AC，∠BCA＝65°，作CD∥AB，并与⊙O相交于点D，连接BD，则∠DBC的大小为(A)A．15° B．35° C．25° D．45°6．(2018·河北模拟)如图，分别延长圆内接四边形ABDE的两组对边，延长线相交于点F，C.若∠F＝27°，∠A＝53°，则∠C的度数为(C)A．30° B．43° C．47° D．53°相切，另一边与圆盘边缘两个交点处的读数分别是“4”和“16”(单位：cm)，请你帮小华算出圆盘的半径是10cm.8．(2017·临沂)如图，∠BAC的平分线交△ABC的外接圆于点D，∠ABC的平分线交AD于点E.(1)求证：DE＝DB；(2)若∠BAC＝90°，BD＝4，求△ABC外接圆的半径．解：(1)证明：∵AD 平分∠BAC，BE 平分∠ABC， ∴∠BAE＝∠CAD，∠ABE＝∠CBE. ∴BD ︵＝CD ︵.∴∠DBC＝∠BAE.∵∠DBE＝∠CBE＋∠DBC，∠DEB＝∠ABE＋∠BAE, ∴∠DBE＝∠DEB. ∴DE＝DB. (2)连接CD.∵BD ︵＝CD ︵，∴CD＝BD ＝4. ∵∠BAC＝90°，∴BC 是直径． ∴∠BDC＝90°.9BD 为直径的圆交AC 于点A ．3 5 D ．，利用△ADF∽△CAB，△DEF∽△DBA 10︵交AC 于点F ，DB 交AC 于点11．(2是小明制作的一副弓箭，点A ，D 分别是弓臂BAC BC ＝60 cm .沿AD 方向拉动弓弦的过程中，假设弓臂BAC 始终保持圆弧形，弓弦不伸长．如图2，当弓箭从自然状态的点D 拉到点D 1时，有AD 1＝30 cm ，∠B 1D 1C 1＝120°.(1)图2中，弓臂两端B 1，C 1的距离为3cm ；(2)如图3，将弓箭继续拉到点D 2，使弓臂B 2AC 2为半圆，则D 1D 2.12．如图所示，AB 为⊙O 的直径，CD 为弦，且CD⊥AB，垂足为H.(1)如果⊙O 的半径为4，CD ＝43，求∠BAC 的度数； (2)若点E 为ADB ︵的中点，连接OE ，CE.求证：CE 平分∠OCD；(3)在(1)的条件下，圆周上到直线AC 的距离为3的点有多少个？并说明理由．解：(1)∵AB 为⊙O 的直径，CD⊥AB，∴CH＝12CD ＝2 3.在Rt △COH 中，sin ∠COH＝CH OC ＝32，∴∠COH＝60°.∴∠BAC＝12∠COH＝30°.(2)证明：∵点E 是ADB ︵的中点，∴OE⊥AB. 又∵CD⊥AB，∴OE∥CD.∴∠ECD＝∠OEC. 又∵OE＝OC ，∴∠OEC＝∠OCE. ∴∠OCE＝∠DCE，即CE 平分∠OCD.(3)圆周上到直线AC 的距离为3的点有2个．因为AC ︵上的点到直线AC 的最大距离为2，ADC ︵上的点到直线AC 的最大距离为6，2＜3＜6，根据圆的轴对称性，ADC ︵到直线AC 的距离为3的点有2个．。