空间直线与平面平行的判定PPT

格式：ppt
大小：710.50 KB
文档页数：13

下载文档原格式

直线、平面平行的判定及其性质课件

思考6：设直线a，b为异面直线，经过
直线a可作几个平面与直线b平行？过a，
b外一点P可作几个平面与直线a，b都
平行？
a
b
p
b a a
p b
理论迁移
例1 在空间四边形ABCD中，E，F分别是 AB，AD的中点，求证：EF//平面BCD.
A E B
F D
C
例2 在长方体ABCD—A1B1C1D1中. （1）作出过直线AC且与直线BD1平行的
思考4：有一块木料如图，
E
P为面BCEF内一点，要求过点P在平面BCEF内画一
F
P D
条直线和平面ABCD平行，
那么应如何画线？
A
C B
思考5：如图，设直线b在平面α内，直线a在平面α外，猜想在什么条件下直线 a与平面α平行？
a
a//b
α
b
探究（二）：直线与平面平行的判断定理
思考1：如果直线a与平面α内的一条直线b平行，则直线a与平面α一定平行吗？
D′
A′
P
C′
B′ D
C
A
B
例2 已知平面外的两条平行直线中的一条平行于这个平面，求证另一条也平行于这个平面.
如图，已知直线a，b
和平面α ，a∥b，
a
b
a∥α , a，b都在平面α外 .
c α
求证：b∥α .
作业: P61练习，习题2.2A组：1，2. （做在书上） P62习题2.2A组：5，6. P63习题2.2B组：1，2.
由此可得什么推论？
推论如果一个平面内有两条相交直线分别平行于另一
a
b
α
个平面内的两条直
线，那么这两个平 β

7.3空间直线平面的平行课件高三数学一轮复习

训练1 如图所示，已知四边形ABCD是正方形，四边形 ACEF是矩形，M是线段EF的中点. (1)求证：AM∥平面BDE；
证明如图，记AC与BD的交点为O，连接OE. 因为O，M分别为AC，EF的中点，四边形ACEF是矩形，所以四边形AOEM是平行四边形，所以AM∥OE. 又因为OE⊂平面BDE，AM⊄平面BDE，所以AM∥平面BDE.
(2)平面BDE∥平面MNG. 证明因为N，G分别为平行四边形ADEF的边AD，EF的中点，所以DE∥NG，又DE⊄平面MNG，NG⊂平面MNG，所以DE∥平面MNG. 因为M为AB的中点，N为AD的中点，所以MN为△ABD的中位线，所以BD∥MN，又BD⊄平面MNG，MN⊂平面MNG，所以BD∥平面MNG，又DE与BD为平面BDE内的两条相交直线，所以平面BDE∥平面MNG.
行
图形表示
符号表示
a⊂β，b⊂β， a∩b＝P，a∥α， b∥α⇒α∥β
两个平面平行，则其中一性质个平面内的直线__平__行__于
另一个平面
两个平面平行，如果另一性质个平面与这两个平面_相__交__，定理那么两条__交__线__平行
α∥β， a⊂α⇒a∥β
α∥β，α∩γ＝a， β∩γ＝b⇒a∥b
例 4 如图，在四棱锥 P－ABCD 中，AD∥BC，AB＝BC＝21AD，E，F，H 分别
为线段 AD，PC，CD 的中点，AC 与 BE 交于 O 点，G 是线段 OF 上一点.
(1)求证：AP∥平面 BEF；
证明如图，连接 EC，因为 AD∥BC，BC＝12AD，所以BC∥AE，BC＝AE，所以四边形ABCE是平行四边形，所以O为AC的中点. 又因为F是PC的中点，所以FO∥AP，因为FO⊂平面BEF，AP⊄平面BEF，所以AP∥平面BEF.

直线和平面平行的判定定理ppt课件

直线和平面平行的判定定理ppt课件
2024/1/28
1
目录
2024/1/28
• 直线与平面平行基本概念 • 判定定理一：斜率相等法 • 判定定理二：向量共线法 • 判定定理三：距离相等法 • 综合应用与拓展 • 总结回顾与课堂互动
2
直线与平面平行基
01
本概念
2024/1/28
3
直线与平面定义
及特殊情况的处理。
15
判定定理三：距离
04
相等法
2024/1/28
16
距离相等法原理
直线与平面平行时，直线上任意一点到平面的距离都相等。
利用这一性质，可以通过比较直线上不同点到平面的距离是否相等来判断直线与平面是否平行。
2024/1/28
17
点到直线距离公式
点$P(x_0, y_0, z_0)$到平面 $Ax + By + Cz + D = 0$的距离公式为
2024/1/28
$d = frac{|Ax_0 + By_0 + Cz_0 + D|}{sqrt{A^2 + B^2 + C^2}}$
其中，$A, B, C$是平面方程中的系数，$D$是常数项。
18
实例分析与讨论
实例1
已知直线$l$的方程为$frac{x-1}{2} = frac{y-2}{3} = frac{z-3}{4}$，平面$pi$的方程为$x + y + z = 6$，判断直线$l$与平面$pi$是否平行。
解
在直线$m$上任取两点$Q_1(-1,2,0)$和$Q_2(0,1,1)$，分别计算它们到平面 $alpha$的距离$d_3$和$d_4$。根据点到平面的距离公式，有

直线与平面平行及性质课件-高一下学期数学人教A版(2019)必修第二册

D C
O
A
B
技巧点拨：中点问题可考虑利用中位线的性质解决.
例3、如图，四棱锥P-ABCD中，底面ABCD是平行四边形，E、F 分别是AB，PC的中点，求证：EF//平面PAD
技巧点拨：可通过构造平行四边形寻找平行线.
如果一条直线和一个平面平行，那么这条直线和这个平面内的直线有怎样的位置关系？
•CD//AB →→ •CD//平面α
直线与平面平行的判定定理：
如果平面外一条直线与此平面内的一条直线平行，那么该直线与此平面平行
例2、求证：空间四边形相邻两边中点的连线,平行于经过另两边的平面. 解题流程：画图→写出已知求证→作出辅助线→证明
已知:空间四边形ABCD中，E、F分别是AB，AD的中点. 求证：EF∥平面BCD.
点，求证:四边形EFGH是平行四边形.
A
EH // GF
H E
D
B
G
F C
探究：若加上条件AC=BD,那么四边形EFGH为什么图形?
2.等角定理
A’
E’
D’
A
E
D
如果空间中两个角的两条边分别对应平行，那么这两个角相等或互补.
推论：
如果两条相交直线和另两条相交直线分别平行，那么这两组直线所成的锐角（或直角）相等.
a
α
平行或异面
三、直线与平面平行的性质定理
一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行.
βa
αb
线面平行
先找平面再线找线两平平行面的交线
例4、有一块木料如图，已知棱BC平行于面A′C′ （1）要经过木料表面A′B′C′D′内的一点P和棱BC将木料
锯开，应怎样画线？（2）所画的线和面AC有什么关系？

直线与平面平行的判定说课课件_图文

随堂练习
活动:
①让学生准备一张便于折叠的三角形的纸,沿顶点任意折叠,做成空间四边形,并标出相邻两边的中点,观察连线与另外一个三角形所在平面的位置关系. ②再让学生标出相邻两边的三等分点、四等分点,观察连线与另外一个三角形所在平面的位置关系.
例1:
求证：空间四边形相邻两边中点的连线平行于经过另外两边所在的平面．
变式:
1.如图，在空间四边形ABCD中，E、F分
别为AB、AD上的点，若
，则EF
与平面BCD的位置关系是_E_F_/_/平__面__B_C__D__.
A
F E
D
B
C
1．证明直线与平面平行的方法：
（1）利用定义；
（2）利用判定定理．
线线平行
线面平行
2．数学思想方法：直线与直线平行
平面与平面平行
直线与平面平行
承上启下
说学情说教材说目标说教法说学法
教师教法
启发式
问
题
引导式
为
载
探究式
体
学生学法
活
观察猜想
动
方法探究
为
主
小组合作
线
归纳总结
问题引入
作业布置
实例感受
探究结论
说过程
回顾反思
数学应用
根据公共点的情况，空间中直线a和平面有哪几种位置关系？
直线与平面平行的判定说课课件_图文.ppt
说学情说教材说目标说教法说学法
初步了解
空间点、线、面及其位置关系
基本熟悉直观感知操作确认
提供丰富和直观的观察材料
解决方法
恰当的教学方式和方法

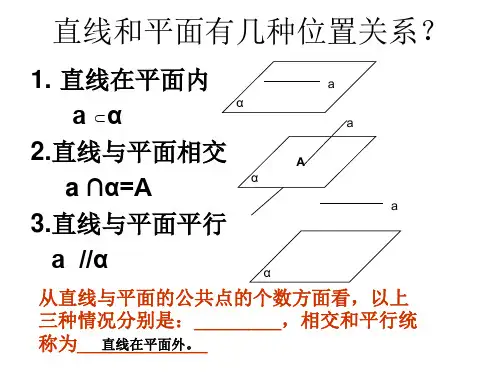
直线与平面平行判定定理课件

A
平面CC’D’D 答：1）平面）平面A’B’C’D’, 平面答：2）平面）平面A’B’C’D’，平面，平面ADD’A’
答：3）平面）平面ADD’A’
问问1 问问2 问问3
D' B'
M D N
C'
若 M， N分分，分为 D'A，D'B的，的中中，则 MN 与平平_____ 平平？
如何判断直线与平面平行？如何判断直线与平面平行？
• 思考1：请大家利用手中的模型，思考1 请大家利用手中的模型，看看有哪些直线与平面是平行的，看看有哪些直线与平面是平行的，理由又是什么？理由又是什么？
如何判断直线与平面平行？如何判断直线与平面平行？
• 思考2：观察门扇转动，或者翻动思考2 观察门扇转动，书的封面这一运动变化过程中，书的封面这一运动变化过程中，有没有某些直线与某些平面平行？没有某些直线与某些平面平行？为什么？什么？ • 观察演示，想想在转动过程中，橡观察演示，想想在转动过程中，皮筋所在的直线与底面是否平行？皮筋所在的直线与底面是否平行？如何摆就能使它们平行？如何摆就能使它们平行？
• 例1、求证：空间四边形相邻两、求证：边中点的连线平行于经过另外两边所在的平面。两边所在的平面。
A E B C F D
例2：P是平行四边形ABCD所在平面外是平行四边形ABCD所在平面外 ABCD 一点， PA的中点求证：PC//平的中点，一点，Q是PA的中点，求证：PC//平面BDQ.
如何判断直线与平面平行？如何判断直线与平面平行？
a
• 思考4：思考4 如果平面外 b α 的一条直线a 的一条直线a与平面内的直线b 平面内的直线b 平行，那么a 平行，那么a平行于平面α吗？

8.5空间直线、平面的平行(1)PPT课件(人教版)

形,BD∩AC=G,∴G是BD的中点.又∵E是
BB1的中点,∴DB1∥GE.又DB1⊄平面
ACE,GE⊂平面ACE,∴B1D∥平面ACE.
变式 (1)如图,四棱锥P-ABCD的底面为平行四边形,M为棱PC的中点.
求证:(1)BC∥平面PAD;
(2)AP∥平面MBD.
证明:(1)因为四棱锥P-ABCD的底面为平行四边形,所以BC∥AD,又BC⊄平面
意可知四边形ABC1D1为平行四边形,则AD1∥BC1.又AD1∥EF,所以EF∥BC1.因
为EF⊄平面BCC1B1,BC1⊂平面BCC1B1,所以EF∥平面BCC1B1.显然正方体的其
余4个面都不与EF平行.故选B.
变式 (3)如图所示,四棱锥S - ABCD的底面是平行四边

形,M,N分别是SA,BD上的点,且 = .求证:MN∥平面

SBC.

证明:连接AN并延长,使之交BC于点P,连接SP.因为AD∥BC,所以 = .又

= ,所以 = ,所以MN∥SP.

因为MN⊄平面SBC,SP⊂平面SBC,所以MN∥平面SBC.
小结
1.利用直线与平面平行的判定定理证明线面平行的一般步骤
解析
思考►►►
如何判定一条直线与一个平面平行？
【解析】如果平面外一条直线与此平面内的一条直线平行，那么该直线与此平面
平行．
解析
直线与平面平行的判定定理：
表示定理
直线与平面
平行的
判定定理
图形
文字
符号
如果平面外一条直线
a⊄α，
与此平面内的一条直
b⊂α，
线平行，那么该直线

空间直线平面的平行课件-2024届高三数学一轮复习

D.A1B1∥NE
)
答案 B
解析 ∵在▱AA1B1B中,AM=MA1,BN=NB1,∴AM=BN.又AM∥BN,
∴四边形ABNM是平行四边形,∴MN∥AB.
又MN⊄平面ABC,AB⊂平面ABC,∴MN∥平面ABC.又MN⊂平面MNEF,平面
MNEF∩平面ABC=EF,∴MN∥EF,∴EF∥AB.在△ABC中,EF≠AB,
∴EF≠MN,∴四边形MNEF为梯形.故选B.
3.设m,n是不同的直线,α,β是不同的平面,则下列命题正确的是(
A.若m∥α,n∥α,则m∥n
B.若m∥α,m∥β,则α∥β
C.若m⊥α,α⊥β,则m∥β
D.若m⊥α,m⊥β,则α∥β
答案 D
解析 A选项,若m∥α,n∥α,则m∥n,或m,n相交或m,n异面,A错误;
EMGHIJ∥平面ACD1,EF∥平面ACD1,则F⊂平面EMGHIJ,观察各选项,ACD
满足.
考点二
线面平行的判定与性质(多考向探究)
考向1.直线与平面平行的判定
典例突破
例2.(2023江西南昌三模)如图,在多面体ABCDEF中,四边形ABCD与ABEF
均为直角梯形,AD∥BC,AF∥BE,DA⊥平面

∴BB1=2CD, =2,
∴OE∥GD,又OE⊄平面AA1C1C,GD⊂平面AA1C1C,
∴OE∥平面AA1C1C.
(2)解连接AC1,则GD∥AC1,OE∥AC1,
∴A,C1,O,E四点共面.
又AO∩BC=F,∴F∈AO,F∈平面AC1EO.
又F∈BC,BC⊂平面BB1C1C,
∴F∈平面BB1C1C.
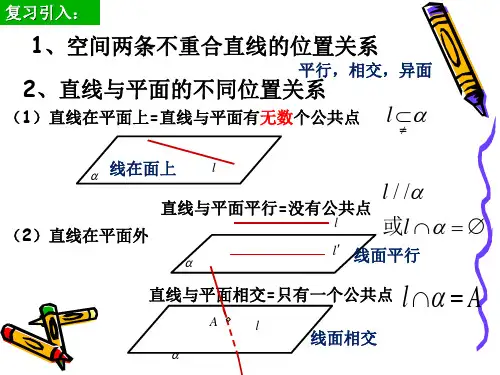
系如何?
提示平行或异面.
2.面面平行的判定与性质

221222直线与平面平面与平面平行的判定定理PPT课件

D1
N
A1
M
F
B1
C1
E
D1 M
A1
N
C1 B1
D A
C B
D
K
A
Q
C
P B
变式
例如图，在棱长为2的正方体ABCD-A1B1C1D1中，E，F 分别为DD1，DB的中点.求证：EF//平面ABC1D1.
证明：如图，连接BD1 ，
D1
C1
在△DBD1中，EF为三角形中位线，
所以EF//BD1 ，
又EF
故A1B//平面ADC1
A1
C1
B1
E
A
C
D B
例如图，四棱锥P-ABCD中，底面ABCD是正方形，M，N分别是 AB，PC的中点,求证：MN//平面PAD.
证明：取PD的中点H，连接HN，AH ， P
在三角形△PDC中，HN为三角形中位线，所以HN//DC且 HN= 1 DC
H
2
D
又因为底面为正方形，且M为AB中点，
②从中你能得出什么结论？
A
B
猜想：如果平面外一条直线和这个平面内的一条直线平行，那么这条直线和这个平面平行.
1.直线与平面平行的判定定理
若平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行.
(1)用该定理判断直线a和平面平行，须具备三个条件：
“面外、面内、平行”
a
a
即
b
a
//
a // b
EF和面BCD哪一条直线平行呢？直线BD
EF D
C
证明：连接BD，
B
∵在△ABD中，E、F分别是AB、AD的中点

空间直线和平面的位置关系ppt课件

a
④求异面直线A1B与B1C1的距离
2a 2Biblioteka 例３：如图，已知长方体ABCD-A’B’C’D’的
棱长AA’=3cm,AB=4cm,AD=5cm.
(1)求点A和C’的距离；
(2)求点A到棱B’C’的距离；
(3)求棱AB和平面A’B’C’D’的距离；
(4)求异面直线AD和A’B’的距离．
D
C
A
B
D’
C’
取一点M，我们把__点__M___到___平__面____的___距___离_____
叫做直线l 和平面的距离。
3)平面和平面的距离：设平面平行于平面β,在平面上任取一点M,我
们把_点__M__到_平__面__β_的__距__离__叫做平面和平面β
的距离。
M
MN
N
4)异面直线的距离
思考:和两条异面直线都垂直的直线有多少条？
练习:1. 选择题:
(1) 直线 m 与平面平行的充分条件是 ( )
A. 直线 m 与平面内一条直线平行;
B. 直线 m 与平面内无数条直线平行; C. 直线 m 与平面内所有直线平行; D. 直线 m 与平面没有公共点;
(2) 过直线 l 外两点,作与 l 平行的平面,这样的平面 ( ) A. 能作无数个; B. 只能作一个;
(2) 过一点有且只有一个平面和一条直线垂直 .
(3) 平面的垂线一定与平面相交,交点就是垂足 .
A
直线和平面垂直，记作
l
2、判定直线和平面垂直的方法（1）根据定义
直线l与平面上的任何直线都垂直
（2）直线和平面垂直的判定定理
定理2:如果直线l与平面上的两条相交直线a,b都垂直，那么直线l与平面垂直.

2022-2023学年高一数学：空间中直线、平面的平行教学课件

l1
l2
2
思考2：如何由直线的方向向量与平面的法向
量表示直线与平面平行关系？
l
设u是直线l的方向向量，
n是平面的法向量，
l , 则l // u n u n 0.
n

思考3：由平面与平面的平行关系，可以得到
平面的法向量有什么关系？
设n1 , n 2分别是平面，的法向量，则
则点 N,E 的坐标分别是
所以 = -
2
2
,-
2
2
2
2
,
2
2
,0 ,(0,0,1).
,1 .
又点 A,M 的坐标分别是( 2, 2,0),
所以 = -
2
2
,-
2
2
2
2
,
,1 .
所以 = ,且 A∉NE,所以 NE∥AM.
又因为NE⊂平面BDE,AM⊄平面BDE,
所以AM∥平面BDE.
则 P(3,0,1),Q(0,2,2),R(3,2,0),S(0,4,1),=(-3,2,1),=(-3,2,1),
∴ = ,∴ ∥ ,
即 PQ∥RS.
(方法 2) = +
1
1
=2 − + 2 1 ,
1
1
= 1 + 1 = 2 1 + 2 − ,
人教A版2019选修第一册
第 1 章空间向量与立体几何
1.4.1 空间中直线、平面的平行
（第2课时）
目
录
01证明面面平行
02证明线面平行
03证明线线平行
学习目标
1、掌握用方向向量，法向量
2、证明线线、线面、面面间的平行关系.

人教A版高中数学必修第二册教学课件PPT-第八章 -8-5-2直线与平面平行

A.1个
B.2个
C.3个
D.4个
D解析由题图知正方体的前、后、左、右四个面都与EF平行.
高中数学必修第二册 RJ·A
4.如图所示，在空间四边形ABCD中，E，F，G，H分别是AB，BC，CD，
DA上的点(不与端点重合)，EH∥FG，则EH与BD的位置关系是
A.平行
B.相交
C.异面
D.不确定
A解析 ∵EH∥FG，EH⊄平面BDC，FG⊂平面BDC， ∴EH∥平面BDC，又EH⊂平面ABD且平面ABD∩平面BDC＝BD， ∴EH∥BD.
高中数学必修第二册 RJ·A
反思感悟
利用直线和平面平行的判定定理证明线面平行的关键是在平面内找一条直线与已知直线平行，常利用平行四边形、三角形中位线、基本事实4等.
高中数学必修第二册 RJ·A
跟踪训练
如图，四边形ABCD是平行四边形，P是平面ABCD外一点，M，N分别是AB，PC的中点.求证：MN∥平面PAD.
所以 a∥EG，即 BD∥EG，所以AACF＝AAEB.
又EBGD＝AAEB，所以AACF＝EBGD，于是 EG＝AFA·CBD＝55×＋44＝290.
高中数学必修第二册 RJ·A
反思感悟
(1)利用线面平行的性质定理找线线平行，利用线线平行得对应线段成比例即可求线段长度. (2)通过定理的运用和平行的性质，提升直观想象和逻辑推理素养.
高中数学必修第二册 RJ·A
典例剖析
一、直线与平面平行的判定定理的应用
例1 如图，在正方体ABCD－A1B1C1D1中，E，F，G分别是BC，CC1，BB1的中点，求证：EF∥平面AD1G.
高中数学必修第二册 RJ·A

直线与平面平行的判定定理(公开课)ppt课件

若两向量的点积为零，则它们垂直。
应用
通过计算直线方向向量与平面法向量的点积，可以判断直线与平面是否平行。
判定定理三：法向量垂直
定义
若一直线与一平面平行，则该直线的法向量与该平面的法向量平行。
推论
若两向量平行，则它们的分量成比例。
应用
通过比较直线法向量与平面法向量的分量比例，可以判断直线与平面是否平行。
直线与平面平行的定义
阐述直线与平面平行的基本概念，为后续判定定理的引入做铺垫。
判定定理的重要性
说明直线与平面平行判定定理在几何学中的地位和作用，以及在实际应用中的价值。
教学目标
80%
知识与技能
掌握直线与平面平行的判定定理及其证明方法，理解相关概念，能够运用所学知识解决相关问题。
100%
过程与方法
应用举例二：判断两平面是否平行
方法一
利用平行平面的性质，通过证明一个平面内有两条相交直线分别与另一个平面平行，从而判定两个平面平行。
方法二
利用向量法，通过计算两个平面的法向量是否共线，从而判定两个平面是否平行。
应用举例三：解决实际问题中的平行问题
1 2
实例一
在建筑设计中，利用直线与平面平行的性质，确保建筑物的立面、地面等各部分保持平行，以达到美观和稳定的效果。
定义
应用
若一直线与一平面平行，则该直线与该平面内任意一条直线的斜率相等。
通过比较直线与平面内某一直线的斜率，可以判断直线与平面是否平行。
推论
若两直线的斜率相等，则它们或者平行或者重合。
判定定理二：方向向量平行
01
02
03
定义
若一直线与一平面平行，则该直线的方向向量与该平面的法向量垂直。

必修第二册8.5.2直线与平面平行课件共18张PPT

线面平行空间问题
例1、求证：空间四边形相邻两边中点的连线平行于经过另外两边所在的平面
已知：如图，空间四边形ABCD中，E、F分别是AB，AD的中点.
求证：EF∥平面BCD.
A
证明：连接BD. 因为AE EB, AF FD 所以EF // BD
E
F
D
B
C
因为EF 平面BCD，BD 平面BCD，
面有没有公共点．
但是，直线无限延长，平面无限延展，如何保证直线与平面没有公共点呢
a
三、观察探究
1、门扇转动的一边与门框所在的平面之间的位置关系．
观察在门扇的旋转过程中: 直线AB在门框所在的平面外直线CD在门框所在的平面内直线AB与CD始终是平行的
A1
A
B1
B
三、观察探究
2、将一本书平放在桌面上，翻动书的封面，封面边缘AB所在直线与桌面所在平面具有什么样的位置关系？
课堂练习
利用平行线分线段成比例定理
1、平面与ABC的两边AB, AC分别交于D, E，且 AD AE ,
DB EC
如图所示，则BC与平面的关系是( A )
A、平行
B、相交
C、异面 D、BC
C
B
E
D
α
A
2、在空间四边形ABCD中，E、F分别是AB和BC上的点，
复习
基本事实4 ：平行于同一条直线的两条直线互相平行。
基本事实4表述的性质通常叫做空间平行线的传递性
b
用符号语言表示如下：
c
a
已知a、b、c三条直线，若a//c，且b//c，则a//b
等角定理：空间中如果有两个角的两边分别对应平行，那么这两个角相等或互补.

数学：2.2.1《直线和平面平行判定》(新人教A版必修2)30张幻灯片

解. 提高学生学习的兴趣，以达到良好的教学效果。
教学过程
单击此处编辑母版标题样式
知识回顾：
1、位置关系
（1）有无数个公共点
直线在平面内
（2）有且只有一个公共点直线与平面相交
（3）没有公共点
直线与平面平行
教学过程
2、直线和平面位置关系的图形表示、符
号表示
a
a
a
α
α
A
α
a aA
a//
教学过程
D A
D A
C B
C B
随堂练习：
课本P56： 2. 如下图，正方体AC1中，E为DD1的中点，试判断BD1与
平面AEC的位置关系，并说明理由。
根据空间问题平面化的思
想，因此把找空间平行直
D1
C1 线问题转化为找平行四边
形或三角形中位线问题，A1这样自然想到了找中点。B1
平行问题找中点解决是个
B1 B
境
为了让学生更清楚地看到线
感
面平行与否的关键因素是什
知
么，使学生学在情境中，思
概
天在花情板理平中面，感悟在内心中，
念
学自己身边的数学，领悟空
间观念与空间图形性质
教学过程
1
创
设
情
境
感受生活中线面平行的例子
感知概念
提出本节学习内容，
·
留下悬念，激发探索求知欲望
球场地面
思考：如何判断一条直线与一个平面平行？
E
F
析证明：连接BD
D
加
深因为 AE=EB，AF=FD，
B
理
C
解所以 EF//BD
又因为 E F 平B面 C ,BD D 平B面 C , D

空间中的平行关系PPT精品课件

答案：平行 5．过三棱柱ABC－A1B1C1任意两条棱的中点作直线，其中与平面ABB1A1平行的直线共有__________条．
答案：6
课堂互动讲练
考点一直线与平面平行的判定
判定直线与平面平行，主要有三种方法：
(1)利用定义(常用反证法)． (2)利用判定定理：关键是找平面内与已知直线平行的直线．可先直观判断平面内是否已有，若没有，则需作出该直线，常考虑三角形的中位线、平行四边形的对边或过已知直线作一平面找其交线．
规律方法总结
2．在解决线面、面面平行的判定时，一般遵循从“低维”到“高维”的转化，即从“线线平行”到“线面平行”，再到“面面平行”；而在应用性质定理时，其顺序恰好相反，但也要注意，转化的方向总是由题目的具体条件而定，决不可过于“模式化”．
规律方法总结
3．在应用有关定理、定义等解决问题时，应当注意规范性训练，即从定理、定义的每个条件开始，培养一种规范、严密的逻辑推理习惯，切不可只求目标，不顾过程，或言不达意，出现推理“断层”的错误．
课堂互动讲练
∴PQ∥EK. 又 PQ⊄平面 BEC，EK⊂面 BEC， ∴PQ∥平面 BEC. 法三：如图所示，作 PH∥EB 交 AB 于 H，连结 HQ，则AHHB＝APEP， ∵AE＝BD，AP＝DQ， ∴PE＝BQ，
∴AH＝AP＝DQ， HB PE BQ
课堂互动讲练
∴HQ∥AD，即HQ∥BC. 又PH∩HQ＝H，BC∩EB＝B， ∴平面PHQ∥平面BCE，而PQ⊂平面PHQ， ∴PQ∥平面BCE.
课堂互动讲练
【名师点评】法一、法二均是依据线面平行的判定定理在平面BCE 内寻找一条直线l，证得它与PQ平行．
特别注意直线l的寻找往往是通过过直线PQ的平面与平面BCE相交的交线来确定．

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

D1
C1
A1
E
B1
F
G
D C
A B
11
练习 3. 如图，已知公共边为 AB 的两个全等的矩形 ABCD 和 ABEF 不在同一平面内，P，Q 分别是对角线 AE，BD 上的点，且 AP＝DQ．求证：PQ∥平面 CBE.
G H
12
反思~领悟
1.线面平行,通常可以转化为线线平行来处理.
2.寻找平行直线可以通过三角形的中位线、梯形的中位线、平行线的判定等来完成。 3.证明的书写三个条件“内”、“外”、“平行”，缺一不可。
直线与平面平行的判定定理：
平面外的一条直线与此平面内的一条直线平行，
则该直线与号表示：
b
①内 b
②外
a
a / /
③平行 a / / b
5
线面平行的判定定理的理解
例1 下列说法中正确的是( ) A．若直线l平行于平面α内的无数条直线，则l∥α B．若直线a在平面α外，则a∥α C．若直线a∥b，b⊂α，则a∥α
例1. 如图，空间四边形ABCD中，E、F分别是
AB，AD的中点.
A
求证：EF∥平面BCD.
分析：只要证一个平面内有
两条相交直线和另一个平面平行即可．
F
E
D
B
线线平行
线面平行
8
线面平行的判定定理的运用
例 2.如图，空间四边形 ABCD 中，E、F、G、H 分别是 AB、BC、CD、 DA 的中点．
13
求证：(1)EH∥平面 BCD；(2)BD∥平面 EFGH.
9
练习 1.如图，P 是▱ABCD 所在平面外一点，E，F 分别为 AB，PD 的中点，求证：AF∥平面 PEC.
P
A BE
F
G
D
C
10
练习 2.如图，在长方体 ABCD-A1B1C1D1中，E, F, G 分别是棱 A1B1, B1C1, DD1 的中点，求证：EF∥平面 ACG.
D．若直线a∥b，b⊂α， a ⊄ α，那么直线a平行于平面α
内的无数条直线
6
线面平行的判定定理的理解
若直线 a 不平行于平面 α，则下列结论成立的是( ) A．α 内的所有直线均与 a 异面 B．α 内不存在与 a 平行的直线 C．α 内直线均与 a 相交 D．直线 a 与平面 α 有公共点
7
线面平行的判定定理的运用
2.2.1
直线与平面平行的判定
1
复习旧知
直线和平面的位置关系
位置关系
公共点
直线 a 在平面α内
有无数个
公共点
直线 a 与平面 α 相交
直线 a 与平面 α 平行
有且只有一个
公共点
没有
公共点
符号表示
a⊂α
a∩α＝A
a∥α
图形表示
2
新课导入
【问题导思】如图，一块矩形木板ABCD的一边AB在平面α内，把这
块木板绕AB转动，在转动过程中，AB的对边CD(不落在α内) 是否都和平面α平行？
3
探究问题，归纳结论
如图，平面外的直线 a平行于平面内的直线b。
（1）这两条直线共面吗？
（2）直线 a与平面相交吗？
a
b
猜想：如果平面外一条直线和这个平面内的一条直线平行，那么这条直线和这个平面平行。 4
归纳结论