平面与平面平行的判定

平面与平面平行的判定和性质第一章：教案简介本章将介绍教案平面与平面平行的判定和性质。

通过本章的学习，学生将能够理解并应用平面与平面平行的判定条件，掌握平面与平面平行的性质，并能够运用这些知识解决实际问题。

第二章：平面与平面平行的判定1. 判定条件一：如果两个平面的法向量互相平行，则这两个平面平行。

2. 判定条件二：如果一个平面经过另一个平面的法向量，则这两个平面平行。

3. 判定条件三：如果两个平面相交于一条直线，且这条直线垂直于两个平面的法向量，则这两个平面平行。

第三章：平面与平面平行的性质1. 性质一：平面与平面平行时，它们的法向量互相平行。

2. 性质二：平面与平面平行时，它们的法向量垂直于它们的交线。

3. 性质三：平面与平面平行时，它们的交线平行于它们的法向量。

第四章：应用举例1. 例一：给定两个平面，如何判断它们是否平行？2. 例二：给定一个平面和一条直线，如何判断这条直线是否与平面平行？3. 例三：给定两个平面和它们的交线，如何判断这两个平面是否平行？第五章：练习题1. 判断题：如果两个平面的法向量互相垂直，则这两个平面平行。

（对/错）2. 判断题：如果一个平面经过另一个平面的法向量，则这两个平面平行。

（对/错）3. 判断题：如果两个平面相交于一条直线，且这条直线垂直于两个平面的法向量，则这两个平面平行。

（对/错）4. 应用题：给定两个平面，它们的法向量分别为向量A和向量B。

判断这两个平面是否平行，并说明理由。

5. 应用题：给定一个平面P和一条直线L。

已知平面P的法向量为向量A，直线L的方向向量为向量B。

判断直线L是否与平面P平行，并说明理由。

第六章：教案平面与平面平行的判定和性质的综合应用1. 综合应用一：如何判断一个平面是否平行于另一个平面的交线？2. 综合应用二：如何判断一条直线是否与另一个平面平行？3. 综合应用三：如何判断两个平面是否平行，并确定它们的交线？第七章：教案平面与平面平行的判定和性质的证明题1. 证明题一：已知平面P和Q，证明平面P与平面Q平行的条件是它们的法向量互相平行。

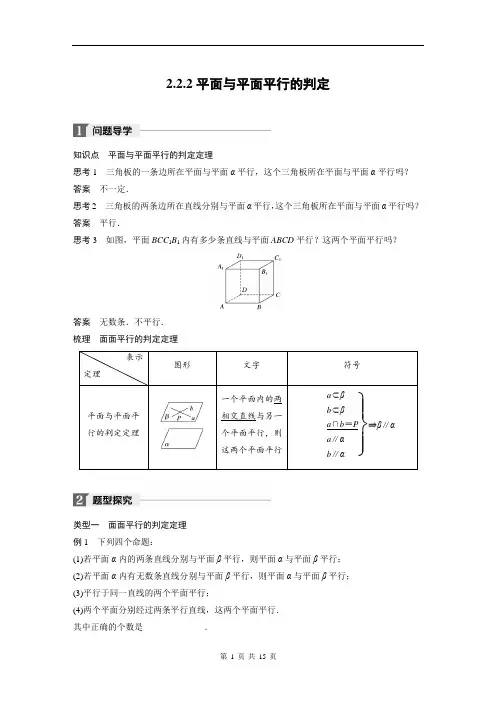
2.2.2平面与平面平行的判定知识点平面与平面平行的判定定理思考1三角板的一条边所在平面与平面α平行，这个三角板所在平面与平面α平行吗？答案不一定．思考2三角板的两条边所在直线分别与平面α平行，这个三角板所在平面与平面α平行吗？答案平行．思考3如图，平面BCC1B1内有多少条直线与平面ABCD平行？这两个平面平行吗？答案无数条．不平行．梳理面面平行的判定定理表示定理图形文字符号平面与平面平行的判定定理一个平面内的两相交直线与另一个平面平行，则这两个平面平行⎭⎪⎬⎪⎫a⊂βb⊂βa∩b＝Pa∥αb∥α⇒β∥α类型一面面平行的判定定理例1下列四个命题：(1)若平面α内的两条直线分别与平面β平行，则平面α与平面β平行；(2)若平面α内有无数条直线分别与平面β平行，则平面α与平面β平行；(3)平行于同一直线的两个平面平行；(4)两个平面分别经过两条平行直线，这两个平面平行．其中正确的个数是______________．答案0反思与感悟在判定两平面是否平行时，一定要强调一个平面内的“两条相交直线”这个条件，线不在多，相交就行．跟踪训练1设直线l, m, 平面α，β，下列条件能得出α∥β的有()①l⊂α，m⊂α，且l∥β，m∥β；②l⊂α，m⊂α，且l∥m，l∥β，m∥β；③l∥α，m∥β，且l∥m；④l∩m＝P, l⊂α，m⊂α，且l∥β，m∥β.A．1个B．2个C．3个D．0个答案 A解析①错误，因为l, m不一定相交；②错误，一个平面内有两条平行直线平行于另一个平面，这两个平面可能相交；③错误，两个平面可能相交；④正确．类型二平面与平面平行的证明例2如图所示，在正方体AC1中，M，N，P分别是棱C1C，B1C1，C1D1的中点，求证：平面MNP∥平面A1BD.证明如图，连接B1C.由已知得A1D∥B1C，且MN∥B1C，∴MN∥A1D.又∵MN⊄平面A1BD，A1D⊂平面A1BD，∴MN∥平面A1BD.连接B1D1，同理可证PN∥平面A1BD.又∵MN⊂平面MNP，PN⊂平面MNP，且MN∩PN＝N，∴平面MNP∥平面A1BD.引申探究若本例条件不变，求证：平面CB1D1∥平面A1BD.证明因为ABCD－A1B1C1D1为正方体，所以DD1綊BB1，所以BDD1B1为平行四边形，所以BD∥B1D1.又BD⊄平面CB1D1，B1D1⊂平面CB1D1，所以BD∥平面CB1D1，同理A1D∥平面CB1D1.又BD∩A1D＝D，所以平面CB1D1∥平面A1BD.反思与感悟判定平面与平面平行的四种常用方法(1)定义法：证明两个平面没有公共点，通常采用反证法．(2)利用判定定理：一个平面内的两条相交直线分别平行于另一个平面．证明时应遵循先找后作的原则，即先在一个平面内找到两条与另一个平面平行的相交直线，若找不到再作辅助线．(3)转化为线线平行：平面α内的两条相交直线与平面β内的两条相交直线分别平行，则α∥β.(4)利用平行平面的传递性：若α∥β，β∥γ，则α∥γ.跟踪训练2如图所示，在三棱柱ABC－A1B1C1中，E，F，G，H分別是AB，AC，A1B1，A1C1的中点，求证：(1)B，C，H，G四点共面；(2)平面EF A1∥平面BCHG.证明(1)因为G，H分别是A1B1，A1C1的中点，所以GH是△A1B1C1的中位线，所以GH∥B1C1.又因为B1C1∥BC，所以GH∥BC，所以B，C，H，G四点共面．(2)因为E，F分别是AB，AC的中点，所以EF∥BC.因为EF⊄平面BCHG，BC⊂平面BCHG，所以EF∥平面BCHG.因为A1G∥EB，A1G＝EB，所以四边形A1EBG是平行四边形，所以A1E∥GB.因为A1E⊄平面BCHG，GB⊂平面BCHG，所以A 1E ∥平面BCHG . 因为A 1E ∩EF ＝E ， 所以平面EF A 1∥平面BCHG .类型三 线线平行与面面平行的综合应用命题角度1 线线、线面、面面平行的相互转化的证明问题例3 如图，在正方体ABCD －A 1B 1C 1D 1中，S 是B 1D 1的中点，E ，F ，G 分别是BC ，DC 和SC 的中点，求证： (1)直线EG ∥平面BDD 1B 1； (2)平面EFG ∥平面BDD 1B 1.证明 (1)如图，连接SB .∵E ，G 分别是BC ，SC 的中点， ∴EG ∥SB .又∵SB ⊂平面BDD 1B 1，EG ⊄平面BDD 1B 1， ∴EG ∥平面BDD 1B 1. (2)连接SD .∵F ，G 分别是DC ，SC 的中点， ∴FG ∥SD .又∵SD ⊂平面BDD 1B 1，FG ⊄平面BDD 1B 1， ∴FG ∥平面BDD 1B 1.又EG ∥平面BDD 1B 1，且EG ⊂平面EFG ，FG ⊂平面EFG ，EG ∩FG ＝G ， ∴平面EFG ∥平面BDD 1B 1.反思感悟 解决线线平行与面面平行的综合问题的策略(1)立体几何中常见的平行关系是线线平行、线面平行和面面平行，这三种平行关系不是孤立的，而是相互联系、相互转化的．(2)线线平行――→判定线面平行――→判定面面平行所以平行关系的综合问题的解决必须灵活运用三种平行关系的判定定理．跟踪训练3 如图所示，在正方体ABCD －A 1B 1C 1D 1中，E ，F ，G ，H 分别为BC ，CC 1，C 1D 1，A 1A 的中点．求证：(1)BF ∥HD 1； (2)EG ∥平面BB 1D 1D ； (3)平面BDF ∥平面HB 1D 1.证明 (1)如图，取BB 1的中点M ，连接C 1M ，HM ，易知HMC 1D 1是平行四边形，∴HD 1∥MC 1， 又由已知可得MC 1∥BF ，∴BF ∥HD 1.(2)取BD 的中点O ，连接OE ，D 1O ，则OE 綊12DC .又D 1G 綊12DC ，∴OE 綊D 1G ，∴四边形OEGD 1是平行四边形，∴GE ∥D 1O . 又D 1O ⊂平面BB 1D 1D ，EG ⊄平面BB 1D 1D ， ∴EG ∥平面BB 1D 1D .(3)由(1)知HD 1∥BF ，又BD ∥B 1D 1，B 1D 1，HD 1⊂平面HB 1D 1，BF ，BD ⊂平面BDF ， 且B 1D 1∩HD 1＝D 1，BD ∩BF ＝B ， ∴平面BDF ∥平面HB 1D 1.命题角度2 线线与面面平行的探索性问题例4 如图所示，在正方体ABCD －A 1B 1C 1D 1中，O 为底面ABCD 的中心，P 是DD 1的中点，设Q 是CC 1上的点，问：当点Q 在什么位置时，平面D 1BQ ∥平面P AO ?解 当Q 为CC 1的中点时，平面D 1BQ ∥平面P AO .∵Q 为CC 1的中点，P 为DD 1的中点，连接PQ ，如图，易证四边形PQBA 是平行四边形，∴QB ∥P A .又∵AP ⊂平面APO ，QB ⊄平面APO ，∴QB ∥平面APO .∵P ，O 分别为DD 1，DB 的中点，∴D 1B ∥PO . 同理可得D 1B ∥平面P AO ， 又D 1B ∩QB ＝B ， ∴平面D 1BQ ∥平面P AO .反思感悟 对于探索性问题，一是可直接运用题中的条件，结合所学过的知识探求；二是可先猜想，然后证明猜想的正确性．跟踪训练4 在底面是平行四边形的四棱锥P －ABCD 中，点E 在PD 上，且PE ∶ED ＝2∶1，M 为PE 的中点，在棱PC 上是否存在一点F ，使平面BFM ∥平面AEC ？并证明你的结论．解 当F 是棱PC 的中点时，平面BFM ∥平面AEC . ∵M 是PE 的中点，∴FM ∥CE . ∵FM ⊄平面AEC ，CE ⊂平面AEC ， ∴FM ∥平面AEC . 由EM ＝12PE ＝ED ，得E 为MD 的中点，连接BM ，BD ，如图所示，设BD ∩AC ＝O ，则O 为BD 的中点． 连接OE ，则BM ∥OE .∵BM⊄平面AEC，OE⊂平面AEC，∴BM∥平面AEC.又∵FM⊂平面BFM，BM⊂平面BFM，FM∩BM＝M，∴平面BFM∥平面AEC.1．下列命题中正确的是()A．一个平面内两条直线都平行于另一平面，那么这两个平面平行B．如果一个平面内任何一条直线都平行于另一个平面，那么这两个平面平行C．平行于同一直线的两个平面一定相互平行D．如果一个平面内的无数多条直线都平行于另一平面，那么这两个平面平行答案 B解析如果一个平面内任何一条直线都平行于另一个平面，即两个平面没有公共点，则两平面平行，所以B正确．2．在正方体中，相互平行的面不会是()A．前后相对侧面B．上下相对底面C．左右相对侧面D．相邻的侧面答案 D解析由正方体的模型知前后面、上下面、左右面都相互平行，所以选D.3．在正方体EFGH－E1F1G1H1中，下列四对截面彼此平行的一对是()A．平面E1FG1与平面EGH1B．平面FHG1与平面F1H1GC．平面F1H1H与平面FHE1D．平面E1HG1与平面EH1G答案 A解析如图，∵EG∥E1G1，EG⊄平面E1FG1，E1G1⊂平面E1FG1，∴EG∥平面E1FG1.又G1F∥H1E，同理可证H1E∥平面E1FG1，又H1E∩EG＝E，∴平面E1FG1∥EGH1.4．如图，已知在三棱锥P－ABC中，D，E，F分别是棱P A，PB，PC的中点，则平面DEF 与平面ABC的位置关系是________．答案平行解析在△P AB中，因为D，E分别是P A，PB的中点，所以DE∥AB.又DE⊄平面ABC，因此DE∥平面ABC.同理可证EF∥平面ABC.又DE∩EF＝E，所以平面DEF∥平面ABC.5．如图，在正方体ABCD－A1B1C1D1中，P为DD1中点．能否同时过D1，B两点作平面α，使平面α∥平面P AC？证明你的结论．解能作出满足条件的平面α，其作法如下：如图，连接BD1，取AA1的中点M，连接D1M，则BD1与D1M所确定的平面即为满足条件的平面α.证明如下：连接BD交AC于O，连接PO，则PO∥D1B，故D1B∥平面P AC.又因为M为AA1的中点，所以D1M∥P A，从而D1M∥平面P AC.又因为D1M∩D1B＝D1，D1M⊂α，D1B⊂α，所以α∥平面P AC.证明面面平行的方法：(1)面面平行的定义；(2)面面平行的判定定理：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行；(3)两个平面同时平行于第三个平面，那么这两个平面平行．课时作业一、选择题1．直线l∥平面α，直线m∥平面α，直线l与m相交于点P，且l与m确定的平面为β，则α与β的位置关系是()A．相交B．平行C．异面D．不确定答案 B解析因为l∩m＝P，所以过l与m确定一个平面β.又因l∥α，m∥α，l∩m＝P，所以β∥α.2．α、β是两个不重合的平面，a、b是两条不同的直线，则在下列条件下，可判定α∥β的是()A．α、β都平行于直线a、bB．α内有三个不共线的点到β的距离相等C．a，b是α内两条直线，且a∥β，b∥βD．a，b是两条异面直线且a∥α，b∥α，α∥β，b∥β答案 D解析A错，若a∥b，则不能断定α∥β；B错，若三点不在β的同一侧，α与β相交；C错，若a∥b，则不能断定α∥β.故选D.3．已知m，n是两条直线，α，β是两个平面，有以下命题：①m，n相交且都在平面α，β外，m∥α，m∥β，n∥α，n∥β，则α∥β；②若m∥α，m∥β，则α∥β；③若m∥α，n∥β，m∥n，则α∥β.其中正确命题的个数是()A．0 B．1 C．2 D．3答案 B解析设m∩n＝P，记m与n确定的平面为γ.由题意知：γ∥α，γ∥β，则α∥β.故①正确．②、③均错误．4．在正方体ABCD－A1B1C1D1中，M为棱A1D1的动点，O为底面ABCD的中心，E、F分别是A1B1、C1D1的中点，下列平面中与OM扫过的平面平行的是()A．面ABB1A1B．面BCC1B1C．面BCFE D．面DCC1D1答案 C解析取AB、DC的中点分别为E1和F1，OM扫过的平面即为面A1E1F1D1(如图)，故面A1E1F1D1∥面BCFE.5．六棱柱ABCDEF－A1B1C1D1E1F1的底面是正六边形，则此六棱柱的面中互相平行的有()A．1对B．2对C．3对D．4对答案 D解析由图知平面ABB1A1∥平面EDD1E1，平面BCC1B1∥平面FEE1F1，平面AFF1A1∥平面CDD1C1，平面ABCDEF∥平面A1B1C1D1E1F1，∴此六棱柱的面中互相平行的有4对．6．在正方体ABCD－A1B1C1D1中，E，F，G分别是A1B1，B1C1，BB1的中点，给出下列四个推断：①FG∥平面AA1D1D；②EF∥平面BC1D1；③FG∥平面BC1D1；④平面EFG∥平面BC1D1.其中推断正确的序号是()A．①③B．①④C．②③D．②④答案 A解析∵在正方体ABCD－A1B1C1D1中，E，F，G分别是A1B1，B1C1，BB1的中点，∴FG∥BC1. ∵BC1∥AD1，∴FG∥AD1，∵FG⊄平面AA1D1D，AD1⊂平面AA1D1D，∴FG∥平面AA1D1D，故①正确；∵EF∥A1C1，A1C1与平面BC1D1相交，∴EF与平面BC1D1相交，故②错误；∵FG∥BC1，FG⊄平面BC1D1，BC1⊂平面BC1D1，FG∥平面BC1D1，故③正确；∵EF与平面BC1D1相交，∴平面EFG与平面BC1D1相交，故④错误．故选A.7．如图是四棱锥的平面展开图，其中四边形ABCD为正方形，E，F，G，H分别为P A，PD，PC，PB的中点，在此几何体中，给出下面四个结论：①平面EFGH∥平面ABCD；②平面P AD∥BC；③平面PCD∥AB；④平面P AD∥平面P AB. 其中正确的有()A．①③B．①④C．①②③D．②③答案 C解析把平面展开图还原为四棱锥如图所示，则EH∥AB，所以EH∥平面ABCD.同理可证EF∥平面ABCD，所以平面EFGH∥平面ABCD；平面P AD，平面PBC，平面P AB，平面PDC 均是四棱锥的四个侧面，则它们两两相交．∵AB∥CD，∴平面PCD∥AB.同理平面P AD∥BC.二、填空题8．已知平面α、β和直线a、b、c，且a∥b∥c，a⊂α，b、c⊂β，则α与β的关系是_____．答案相交或平行解析b、c⊂β，a⊂α，a∥b∥c，若α∥β，满足要求；若α与β相交，交线为l，b∥c∥l，a∥l，满足要求，故答案为相交或平行．9．已知平面α和β，在平面α内任取一条直线a，在β内总存在直线b∥a，则α与β的位置关系是________．答案平行解析假若α∩β＝l，则在平面α内，与l相交的直线a，设a∩l＝A，对于β内的任意直线b，若b过点A，则a与b相交，若b不过点A，则a与b异面，即β内不存在直线b∥a.故α∥β. 10．已知a和b是异面直线，且a⊂平面α，b⊂平面β，a∥β，b∥α，则平面α与β的位置关系是________．答案平行解析在b上任取一点O，则直线a与点O确定一个平面γ，设γ∩β＝l，则l⊂β，∵a∥β，∴a与l无公共点，∴a∥l，∴l∥α.又b∥α，根据面面平行的判定定理可得α∥β.三、解答题11．如图，在正方体ABCD－A1B1C1D1中，M，N，P分别是C1C，B1C1，C1D1的中点，求证：平面PMN∥平面A1BD.证明连接B1D1，B1C.∵P，N分别是D1C1，B1C1的中点，∴PN∥B1D1.又B1D1∥BD，∴PN∥BD.又PN⊄平面A1BD，BD⊂平面A1BD，∴PN∥平面A1BD.同理，MN∥平面A1BD.又PN∩MN＝N，∴平面PMN∥平面A1BD.12．已知四棱锥P－ABCD中，底面ABCD为平行四边形，点M，N，Q分别在P A，BD，PD 上，且PM∶MA＝BN∶ND＝PQ∶QD.求证：平面MNQ∥平面PBC.证明∵PM∶MA＝BN∶ND＝PQ∶QD，∴MQ∥AD，NQ∥BP，而BP⊂平面PBC，NQ⊄平面PBC，∴NQ∥平面PBC.又∵四边形ABCD为平行四边形，∴BC∥AD，∴MQ∥BC，而BC⊂平面PBC，MQ⊄平面PBC，∴MQ∥平面PBC.易知MQ∩NQ＝Q，根据平面与平面平行的判定定理，可知平面MNQ∥平面PBC.13．如图，在四棱锥C－ABED中，四边形ABED是正方形，G，F分别是线段EC，BD的中点．(1)求证：GF∥平面ABC；(2)若点P为线段CD的中点，平面GFP与平面ABC有怎样的位置关系？并证明．(1)证明如图，连接AE，由F是线段BD的中点得F为AE的中点，∴GF为△AEC的中位线，∴GF∥AC.又∵AC⊂平面ABC，GF⊄平面ABC，∴GF∥平面ABC.(2)解平面GFP∥平面ABC，证明如下：在CD上取中点P，连接FP，GP.∵F，P分别为BD，CD的中点，∴FP为△BCD的中位线，∴FP∥BC.又∵BC⊂平面ABC，FP⊄平面ABC，∴FP∥平面ABC，又GF∥平面ABC，FP∩GF＝F，FP⊂平面GFP，GF⊂平面GFP，∴平面GFP∥平面ABC.四、探究与拓展14．已知l，m是两条不同的直线，α，β是两个不同的平面，有下面四个命题：①若l⊂α，m⊂α，l∥β，m∥β，则α∥β；②若l⊂α，l∥β，α∩β＝m，则l∥m；③若α∥β，l∥α，则l∥β；④若l∥α，m∥l，则m∥α.其中所有真命题的序号是________．答案②解析当l∥m时，平面α与平面β不一定平行，故①错误；②正确；若α∥β，l∥α，则l⊂β或l∥β，故③错误；④中直线m有可能在平面α内，故④错误．15．如图，在直四棱柱ABCD－A1B1C1D1中，底面ABCD为等腰梯形，AB∥CD，且AB＝2CD，在棱AB上是否存在一点F，使平面C1CF∥ADD1A1？若存在，求点F的位置，若不存在，请说明理由．解当F为AB的中点时，平面C1CF∥ADD1A1.理由如下：∵在直四棱柱ABCD－A1B1C1D1中，底面ABCD为等腰梯形，AB∥CD，且AB＝2CD，F为AB的中点，∴CD綊AF綊C1D1，∴AFCD是平行四边形，且AFC1D1是平行四边形，∴CF∥AD，C1F∥AD1.又CF∩C1F＝F，CF，C1F都在平面C1CF内，∴平面C1CF∥平面ADD1A1.。

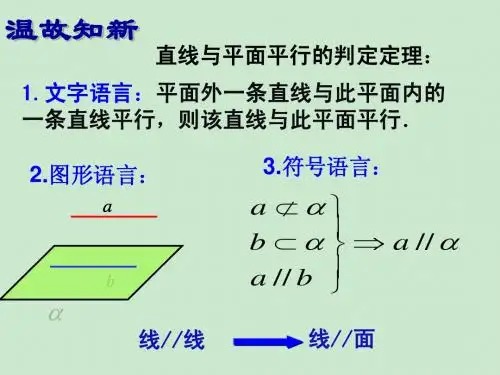
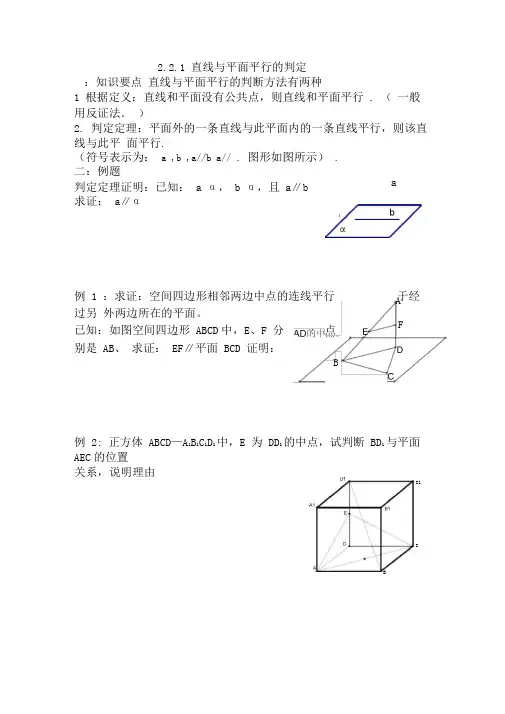
2.2.1 直线与平面平行的判定：知识要点 直线与平面平行的判断方法有两种1 根据定义：直线和平面没有公共点，则直线和平面平行 . （ 一般用反证法． ）2. 判定定理：平面外的一条直线与此平面内的一条直线平行，则该直线与此平 面平行.（符号表示为： a ,b ,a//b a// . 图形如图所示） . 二：例题判定定理证明：已知： a α， b α，且 a ∥b求证： a∥α例 1 ：求证：空间四边形相邻两边中点的连线平行于经过另 外两边所在的平面。

已知：如图空间四边形 ABCD 中，E 、F 分别是 AB 、 求证： EF ∥平面 BCD 证明：例 2: 正方体 ABCD —A 1B 1C 1D 1中，E 为 DD 1的中点，试判断 BD 1与平面AEC 的位置 关系，说明理由a AF点 BC1CB三练习：1. 判断下列说法是否正确，并说明理由．○1 平面 外的一条直线 a 与平面 内的无数条直线平行则直线 a 和平面 平行；○2平面 外的两条平行直线 a,b ，若 a// ，则b// ；○3 直线a 和平面 平行，则直线 a 平行于平面 内任意一条直线； ○4 直线 a 和平面 平行，则平面 中必定存在直线与直线 a 平行． A. l 1 ∥α B. l 2 α C. l 2 ∥α或l 2 α D. l 2 与α相交 3．以下说法（其中 a ，b 表示直线， 表示平面）①若 a ∥b ， b ，则 a ∥ ②若 a ∥ ，b ∥ ，则 a ∥b ③若 a ∥b ， b ∥ ，则 a ∥ ④若 a ∥ ，b ，则 a ∥b 其中正确说法的个数是（ ） .A. 0 个B. 1 个C. 2 个D. 3 个4.已知a ，b 是两条相交直线， a ∥ ，则 b 与 的位置关系是（ ）. A. b ∥ B. b 与 相交 C. b α D. b ∥ 或 b 与 相交5. 如果平面 外有两点 A 、B ，它们到平面 的距离都是 a ，则直线 AB 和平面 的 位置关系一定是（ ） .A. 平行B. 相交C. 平行或相交D. AB 6．平面 与△ ABC 的两边 AB 、 AC 分别交于 D 、E ，且 AD ∶DB=AE ∶EC ，求证： BC ∥平面 .7．P 是平行四边形 ABCD 所在平面外一点， E 为PB 的中点， O 为 AC ，BD 的交点. （1）求证：EO ‖平面PCD ； （2）图中EO 还与哪个平 面平行？8. 在正方体 ABCD- A 1B 1C 1D 1中， E 、F 分别为棱 BC 、C 1D 1的中点. 求证： EF ∥平面 BB 1D 1D2. 已知直线 l 1、l 2 , 平面α, l 1 ∥l 2 , l 1∥α 那么 l 2 与平面 α 的关系是（ ）.2.2 平面与平面平行的判定：知识要点平面与平面平行的判断方法有三种 1. 定义：两平面没有公共点，则两平面平行2. 判定定理：如果一个平面内有两条相交直线都平行于另一个平面， 那么这两个平面平行． 用符号表示为： a ,b ,a b P // a// ,b// 图形如图所示图形如图所示 3. 推论：①如果一个平面内有两条相交直线分别平行于 另一个平面内的两条直线，那么这两个平面平行 ②垂直于同一条直线的两个平面平行 . ③平行与同一平面的两个平面平行 . 二：例题 判定定理证明 : 已知：如图， m ， n ， 求证：//mn ( 思考 1 ：如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线， 那么这两个平面平行吗 ?为什么？ )(思考 2：.在判断一个平面是否水平时，把水准器在这个平 面内交叉地放两次，如果水准器的气泡都是居中的，就 可以判定这个平面和水平面平行，你能说出理由吗？) 例 2：已知正方体 ABCD-A 1B 1C 1D 1, 求证：平面 AB 1D 1 // 平面 C 1BD 。

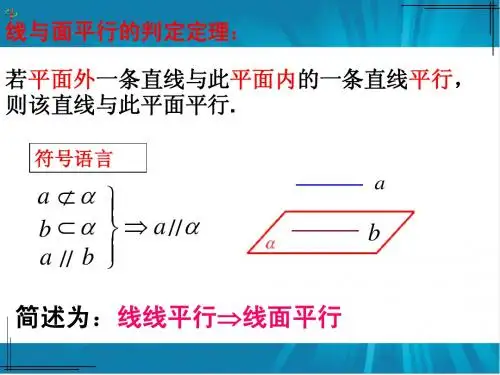
8.5.3 平面与平面平行第一课时平面与平面平行的判定课标要求素养要求1.借助长方体，通过直观感知，归纳出平面与平面平行的判定定理，并加以证明.2.会应用平面与平面平行的判定定理证明平面与平面平行.在发现、推导和应用平面与平面平行的判定定理的过程中，发展学生的数学抽象素养、逻辑推理素养和直观想象素养.教材知识探究贴瓷砖的工人在检验地面是否水平时，只需将水准器交叉放两次，若水准器的气泡都居中就能判定地面是水平的.问题(1)这个实例给出了判断两平面平行的一种怎样的方法？(2)若一个平面内有两条直线平行于另一个平面，那么这两个平面平行吗？提示(1)在一个平面内找两条相交线，分别平行于另一个平面即可.(2)不一定，这两个平面也可能相交.平面与平面平行的判定定理注意定理条件中直线a和b相交文字语言如果一个平面内的两条相交直线与另一个平面平行，那么这两个平面平行符号语言a⊂β，b⊂β，a∩b＝P，a∥α，b∥α⇒β∥α图形语言教材拓展补遗[微判断]1.若一个平面内有无数条直线都与另一个平面平行，则这两个平面平行.(×)2.若一个平面内任何一条直线都平行于另一个平面，则这两个平面平行.(√)3.若α∥β，β∥γ，则α∥γ.(√)4.若a⊂α，α∥β，则a∥β.(√)提示 1.两平面也可能相交.[微训练]在正方体EFGH－E1F1G1H1中，下列四对截面彼此平行的一对是()A.平面E1FG1与平面EGH1B.平面FHG1与平面F1H1GC.平面F1H1H与平面FHE1D.平面E1HG1与平面EH1G解析如图，∵EG∥E1G1，EG平面E1FG1，E1G1⊂平面E1FG1，∴EG∥平面E1FG1.又G1F∥H1E，同理可证H1E∥平面E1FG1，又H1E∩EG＝E，H1E，EG⊂平面EGH1，∴平面E1FG1∥平面EGH1.答案 A[微思考]1.三角板的一条边所在平面与平面α平行，这个三角板所在平面与平面α平行吗？提示不一定.2.三角板的两条边所在直线分别与平面α平行，这个三角板所在平面与平面α平行吗？提示平行.3.如果一个平面内的两条相交直线与另一个平面内的两条相交直线分别对应平行，那么这两个平面平行吗？提示平行(请自己试着证明).题型一面面平行判定定理的理解抓住面面平行判定定理的5个条件，缺一不可【例1】α，β是两个不重合的平面，在下列条件下，可判定α∥β的是()A.α，β都平行于直线l，mB.α内有三个不共线的点到β的距离相等C.l，m是α内的两条直线且l∥β，m∥βD.l，m是异面直线且l∥α，m∥α，l∥β，m∥β解析对A，当α∩β＝a，l∥m∥a时，不能推出α∥β；对B，当α∩β＝a，且在平面α内同侧有两点，另一侧有一个点，三点到平面β的距离相等时，不能推出α∥β；对C，当l∥m时，不能推出α∥β；对D，∵l，m是两条异面直线，且l∥α，m∥α，l∥β，m∥β，∴α内存在两条相交直线与平面β平行，故可得α∥β.答案 D规律方法(1)在判定两个平面是否平行时，一定要强调一个平面内的“两条相交直线”这个条件，线不在多，相交就行.(2)借助于常见几何体(如正方体)进行分析.【训练1】如果一个锐角的两边与另一个角的两边分别平行，下列结论一定成立的是()A.这两个角相等B.这两个角互补C.这两个角所在的两个平面平行D.这两个角所在的两个平面平行或重合答案 D题型二平面与平面平行的证明线∥面⇒面∥面【例2】如图，在多面体ABCDEF中，底面ABCD是平行四边形，点G和点H 分别是CE和CF的中点.证明：平面BDGH∥平面AEF.证明在△CEF中，因为G，H分别是CE，CF的中点，所以GH∥EF，又因为GH平面AEF，EF⊂平面AEF，所以GH∥平面AEF.设AC∩BD＝O，连接OH，在△ACF中，因为OA＝OC，CH＝HF，所以OH∥AF，又因为OH平面AEF，AF⊂平面AEF，所以OH∥平面AEF.又因为OH∩GH＝H，OH，GH⊂平面BDGH，所以平面BDGH∥平面AEF.规律方法平面与平面平行的判定方法(1)定义法：两个平面没有公共点.(2)判定定理：一个平面内的两条相交直线分别平行于另一个平面.(3)转化为线线平行：平面α内的两条相交直线与平面β内的两条相交直线分别平行，则α∥β.(4)利用平行平面的传递性：若α∥β，β∥γ，则α∥γ.【训练2】在正四棱台ABCD－A1B1C1D1中，A1B1＝a，AB＝2a，AA1＝2a，E，F分别是AD，AB的中点.证明：平面EFB1D1∥平面BDC1.证明 连接A 1C 1，AC ，分别交B 1D 1，EF ，BD 于M ，N ，P ，连接MN ，C 1P .由题意，BD ∥B 1D 1. ∵BD平面EFB 1D 1，B 1D 1⊂平面EFB 1D 1， ∴BD ∥平面EFB 1D 1， 又∵A 1B 1＝a ，AB ＝2a ， ∴MC 1＝12A 1C 1＝22a .又∵E ，F 分别是AD ，AB 的中点， ∴NP ＝14AC ＝22a . ∴MC 1＝NP .又∵AC ∥A 1C 1，∴MC 1∥NP . ∴四边形MC 1PN 为平行四边形. ∴PC 1∥MN . ∵PC 1平面EFB 1D 1，MN ⊂平面EFB 1D 1，∴PC 1∥平面EFB 1D 1，∵PC 1∩BD ＝P ，PC 1，BD ⊂平面BDC 1， ∴平面EFB 1D 1∥平面BDC 1.题型三 线面平行与面面平行的综合应用 探究1 面面平行中点的位置的确定【例3－1】 在正方体ABCD －A 1B 1C 1D 1中，O 为BD 的中点，P 是DD 1的中点，设Q 是CC 1上的点，问：当点Q 在什么位置时，平面D 1BQ ∥平面P AO?解当Q为C1C的中点时，平面D1BQ∥平面P AO.证明如下：在△DBD1中，P是DD1中点，O为DB中点，∴PO∥D1B，又∵PO⊂平面P AO，D1B平面P AO，∴D1B∥平面P AO.在正方体中，BQ∥AP，BQ平面P AO，P A⊂平面P AO，∴BQ∥平面P AO，又∵D1B∩BQ＝B，D1B，BQ⊂平面D1BQ，∴平面D1BQ∥平面P AO，即当点Q为C1C的中点时，平面D1BQ∥平面P AO. 探究2平行关系的探究【例3－2】已知点S是正三角形ABC所在平面外的一点，且SA＝SB＝SC，SG 为△SAB中AB上的高，D，E，F分别是AC，BC，SC的中点，试判断SG与平面DEF的位置关系，并给予证明.证明分析可知SG∥平面DEF.证明如下：法一连接CG，交DE于点H，连接FH.∵DE 是△ABC 的中位线， ∴DE ∥AB .在△ACG 中，D 是AC 的中点，且DH ∥AG ， ∴H 为CG 的中点.∵F 是SC 的中点，∴FH 是△SCG 的中位线，∴FH ∥SG . 又SG平面DEF ，FH ⊂平面DEF ，∴SG ∥平面DEF .法二 ∵EF 为△SBC 的中位线，∴EF ∥SB . ∵EF平面SAB ，SB ⊂平面SAB ，∴EF ∥平面SAB .同理可得DF ∥平面SAB .又EF ∩DF ＝F ，EF ，DF ⊂平面DEF ， ∴平面SAB ∥平面DEF .又SG ⊂平面SAB ，∴SG ∥平面DEF .规律方法 解决线面平行与面面平行的综合问题的策略(1)立体几何中常见的平行关系是线线平行、线面平行和面面平行，这三种平行关系不是孤立的，而是相互联系、相互转化的. (2)线线平行――→判定线面平行――→判定面面平行所以平行关系的综合问题的解决必须灵活运用三种平行关系的判定定理.【训练3】 如图所示，P 是△ABC 所在平面外的一点，点A ′，B ′，C ′分别是△PBC ，△PCA ，△P AB 的重心.(1)求证：平面ABC ∥平面A ′B ′C ′； (2)求△A ′B ′C ′与△ABC 的面积之比.(1)证明 分别连接P A ′，PB ′，PC ′并延长交BC ，AC ，AB 于点D ，E ，F ，连接DE ，EF ，DF .∵点A′，C′分别是△PBC，△P AB的重心，∴P A′＝23PD，PC′＝23PF，∴A′C′∥DF.∵A′C′平面ABC，DF⊂平面ABC，∴A′C′∥平面ABC.同理，A′B′∥平面ABC. 又A′C′∩A′B′＝A′，A′C′，A′B′⊂平面A′B′C′，∴平面ABC∥平面A′B′C′.(2)解由(1)知A′C′∥DF且A′C′＝23DF，又DF∥AC且DF＝12AC，∴A′C′∥AC且A′C′＝13AC.同理，A′B′∥AB且A′B′＝13AB，B′C′∥BC且B′C′＝13BC，∴△A′B′C′∽△ABC，∴S△A′B′C′∶S△ABC＝1∶9.一、素养落地1.通过探索发现平面与平面平行的判定定理，重点培养数学抽象素养，通过应用平面与平面平行的判定定理，提升逻辑推理素养及直观想象素养.2.平面与平面平行的判定定理的理解(1)平面内两条相交直线a，b，即a⊂α，b⊂α，a∩b＝P.(2)两条相交直线a，b都与平面β平行，即a∥β，b∥β.这两个条件缺一不可.二、素养训练1.在正方体中，相互平行的面不会是()A.前后相对侧面B.上下相对底面C.左右相对侧面D.相邻的侧面解析由正方体的模型知前后面、上下面、左右面都相互平行，故选D.答案 D2.下列命题中正确的是()A.一个平面内三条直线都平行于另一平面，那么这两个平面平行B.如果一个平面内所有直线都平行于另一个平面，那么这两个平面平行C.平行于同一直线的两个平面一定相互平行D.如果一个平面内有几条直线都平行于另一平面，那么这两个平面平行解析如果一个平面内所有直线都平行于另一个平面，即两个平面没有公共点，则两平面平行，故选B.答案 B3.如图，已知在三棱锥P－ABC中，D，E，F分别是棱P A，PB，PC的中点，则平面DEF与平面ABC的位置关系是________.解析在△P AB中，因为D，E分别是P A，PB的中点，所以DE∥AB.又DE平面ABC，AB⊂平面ABC，因此DE∥平面ABC.同理可证EF∥平面ABC. 又DE∩EF＝E，DE，EF⊂平面DEF，所以平面DEF∥平面ABC.答案平行4.如图，在正方体ABCD－A1B1C1D1中，P为DD1中点.能否同时过D1，B两点作平面α，使平面α∥平面P AC？证明你的结论.解能作出满足条件的平面α，其作法如下：如图，连接BD1，取AA1中点M，连D1M，则BD1与D1M所确定的平面即为满足条件的平面α.证明如下：连接BD交AC于O，连接PO，则O为BD的中点，又P为DD1的中点，则PO∥D1B.∵BD1平面P AC，OP⊂平面P AC，故D1B∥平面P AC.又因为M为AA1的中点，故D1M∥P A，又D1M平面P AC，P A⊂平面P AC，从而D1M∥平面P AC.又因为D1M∩D1B＝D1，D1M⊂α，D1B⊂α，所以平面α∥平面P AC.基础达标一、选择题1.下列四个说法中正确的是()A.平面α内有无数个点到平面β的距离相等，则α∥βB.α∩γ＝a，α∩β＝b，且a∥b(α，β，γ分别表示平面，a，b表示直线)，则γ∥βC.平面α内一个三角形三边分别平行于平面β内的一个三角形的三条边，则α∥βD.平面α内的一个平行四边形的两边与平面β内的一个平行四边形的两边对应平行，则α∥β解析由面面平行的判定定理知C正确.答案 C2.如图所示，设E，F，E1，F1分别是长方体ABCD－A1B1C1D1的棱AB，CD，A1B1，C1D1的中点，则平面EFD1A1与平面BCF1E1的位置关系是()A.平行B.相交C.异面D.不确定解析∵A1E∥BE1，A1E平面BCF1E1，BE1⊂平面BCF1E1，∴A1E∥平面BCF1E1. 同理，A1D1∥平面BCF1E1.又A1E∩A1D1＝A1，A1E，A1D1⊂平面EFD1A1，∴平面EFD1A1∥平面BCF1E1.答案 A3.六棱柱ABCDEF－A1B1C1D1E1F1的底面是正六边形，则此六棱柱的面中互相平行的有()A.1对B.2对C.3对D.4对解析由图知平面ABB1A1∥平面EDD1E1，平面BCC1B1∥平面FEE1F1，平面AFF1A1∥平面CDD1C1，平面ABCDEF∥平面A1B1C1D1E1F1，∴此六棱柱的面中互相平行的有4对.答案 D4.在正方体ABCD－A1B1C1D1中，M为棱A1D1上的动点，O为底面ABCD的中心，点E，F分别是A1B1，C1D1的中点，下列平面中与OM扫过的平面平行的是() A.平面ABB1A1 B.平面BCC1B1C.平面BCFED.平面DCC1D1解析取AB，DC的中点分别为点E1和点F1，连接E1F1，则E1F1过点O，OM 扫过的平面即为平面A1E1F1D1(如图)，故平面A1E1F1D1∥平面BCFE.答案 C5.经过平面α外两点，作与α平行的平面，则这样的平面可以作()A.1个或2个B.0个或1个C.1个D.0个解析①当经过两点的直线与平面α平行时，可作出一个平面β使β∥α.②当经过两点的直线与平面α相交时，由于作出的平面与平面α至少有一个公共点，故经过两点的平面都与平面α相交，不能作出与平面α平行的平面.故满足条件的平面有0个或1个.答案 B二、填空题6.已知平面α，β和直线a，b，c，且a∥b∥c，a⊂α，b，c⊂β，则α与β的关系是________________.解析b，c⊂β，a⊂α，a∥b∥c，若α∥β，满足要求；若α与β相交，交线为l，b∥c∥l，a∥l，满足要求，故答案为相交或平行.答案相交或平行7.已知平面α和β，在平面α内任取一条直线a，在β内总存在直线b∥a，则α与β的位置关系是________(填“平行”或“相交”).解析若α∩β＝l，则在平面α内，与l相交的直线a，设a∩l＝A，对于β内的任意直线b，若b过点A，则a与b相交，若b不过点A，则a与b异面，即β内不存在直线b∥a，矛盾.故α∥β.答案平行8.如图是正方体的平面展开图.在这个正方体中，①BM∥平面DE；②CN∥平面AF；③平面BDM∥平面AFN；④平面BDE∥平面NCF.以上四个命题中，正确命题的序号是________.解析以ABCD为下底面还原正方体，如图：则易判定四个命题都是正确的.答案①②③④三、解答题9.在如图所示的几何体中，三个侧面AA1B1B，BB1C1C，CC1A1A都是平行四边形.求证：平面ABC∥平面A1B1C1.证明∵四边形AA1B1B是平行四边形，∴A1B1∥AB，又A1B1平面ABC，AB⊂平面ABC.∴A1B1∥平面ABC，同理B1C1∥平面ABC，而A1B1∩B1C1＝B1，A1B1，B1C1⊂平面A1B1C1，∴平面A1B1C1∥平面ABC.10.如图，已知在四棱锥P－ABCD中，底面ABCD为平行四边形，点M，N，Q 分别在P A，BD，PD上，且PM∶MA＝BN∶ND＝PQ∶QD.求证：平面MNQ∥平面PBC.证明∵PM∶MA＝BN∶ND＝PQ∶QD，∴MQ∥AD，NQ∥BP，而BP⊂平面PBC，NQ平面PBC，∴NQ∥平面PBC. 又∵四边形ABCD为平行四边形，∴BC∥AD，∴MQ∥BC，而BC⊂平面PBC，MQ平面PBC，∴MQ∥平面PBC.又MQ∩NQ＝Q，MQ，NQ⊂平面MNQ，∴平面MNQ∥平面PBC.能力提升11.如图所示，在正方体ABCD－A1B1C1D1中，E，F，G，H分别是棱CC1，C1D1，D1D，CD的中点，N是BC的中点，点M在四边形EFGH的边上及其内部运动，则M满足________时，有MN∥平面B1BDD1.解析连接HN，FH，FN.∵HN∥DB，FH∥D1D，HN∩HF＝H，BD∩DD1＝D，HN，HF⊂平面FHN，DB，DD1⊂平面B1BDD1，∴平面FHN∥平面B1BDD1.∵点M在四边形EFGH的边上及其内部运动，∴M∈FH.答案M在线段FH上12.如图，在四棱锥C－ABED中，四边形ABED是正方形，点G，F分别是线段EC，BD的中点.(1)求证：GF∥平面ABC；(2)若点P为线段CD的中点，平面GFP与平面ABC有怎样的位置关系？并证明.(1)证明如图，连接AE，由F是线段BD的中点，四边形ABED为正方形得F 为AE的中点，∴GF为△AEC的中位线，∴GF∥AC.又∵AC⊂平面ABC，GF平面ABC，∴GF∥平面ABC.(2)解平面GFP∥平面ABC，证明如下：连接FP，GP.∵点F，P分别为BD，CD的中点，∴FP为△BCD的中位线，∴FP∥BC.又∵BC⊂平面ABC，FP平面ABC，∴FP∥平面ABC，又GF∥平面ABC，FP∩GF ＝F，FP⊂平面GFP，GF⊂平面GFP，∴平面GFP∥平面ABC.创新猜想13.(多选题)在正方体ABCD－A1B1C1D1中，点E，F，G分别是棱A1B1，B1C1，BB1的中点，则()A.FG∥平面AA1D1DB.EF∥平面BC1D1C.FG∥平面BC1D1D.平面EFG∥平面BC1D1解析∵在正方体ABCD－A1B1C1D1中，点E，F，G分别是棱A1B1，B1C1，BB1的中点，∴FG∥BC1.∵BC1∥AD1，∴FG∥AD1，又∵FG平面AA1D1D，AD1⊂平面AA1D1D，∴FG∥平面AA1D1D，故选项A正确；∵EF∥A1C1，A1C1与平面BC1D1相交，∴EF与平面BC1D1相交，故选项B错误；∵FG∥BC1，FG平面BC1D1，BC1⊂平面BC1D1，∴FG∥平面BC1D1，故选项C正确；∵EF与平面BC1D1相交，∴平面EFG与平面BC1D1相交，故选项D错误.答案AC14.(多选题)如图是四棱锥的平面展开图，其中四边形ABCD为正方形，点E，F，G，H分别为P A，PD，PC，PB的中点，则在原四棱锥中()A.平面EFGH∥平面ABCDB.BC∥平面P ADC.AB∥平面PCDD.平面P AD∥平面P AB解析把平面展开图还原为四棱锥如图所示，则EH∥AB，又EH平面ABCD，AB⊂平面ABCD，所以EH∥平面ABCD.同理可证EF∥平面ABCD，又EF∩EH＝E，EF，EH⊂平面EFGH，所以平面EFGH∥平面ABCD，故选项A正确；平面P AD，平面PBC，平面P AB，平面PDC是四棱锥的四个侧面，则它们两两相交，故选项D错误；∵AB∥CD，AB平面PCD，CD⊂平面PCD，∴AB∥平面PCD，同理BC∥平面P AD，故选项B，C正确.答案ABC。