模糊控制器汇总
- 格式:docx
- 大小:933.70 KB
- 文档页数:14


摘要交流伺服电机现广泛应用于机械结构的驱动部件和各种数控机床。
PID控制是伺服系统中使用最多的控制模式之一。
尽管传统的PID控制系统构造简单、运转稳定,但交流伺服电机存在非线性的、强耦合。
当参数变动或非线性因素的影响发生变化时,控制不能实时改动,不能满足系统高性能、高精度的要求。
结合模糊控制和传统PID控制成一种新的控制方法--模糊PID控制是解决上述问题的一种很好的途径。
模糊控制器不需要被控对象的数学模型,而是根据之前人为设定的控制要求设计用来控制的决策算法,使用此方式确定控制量。
模糊控制和传统PID控制融合的结果,不单具有模糊控制的高性能,还具备传统PID控制精准度高的长处。
本文对PID控制算法的原理和模糊控制算法作了简要的描述和比较。
指出模糊PID混合控制法,在误差很大时使用模糊控制,在不大时使用PID控制,在MATLAB软件中,对交流伺服系统的位置控制进行了仿真。
结果表明,该控制系统仿真结果与理论上差距较小。
关键词:PID控制;模糊控制;模糊PID控制器;MATLAB第1章绪论1.1 研究课题的任务本课题的任务是了解交流伺服系统,比较并结合两种控制的优点,结合成一种新的控制方式--模糊PID控制。
该控制法在系统输出差距大时采用模糊控制,而在差距较小时采用PID控制。
文章最后给出了模糊PID位置控制的MATLAB响应图,同时给出了常规PID控制下的效果图,并比较分析。
1.3 交流伺服系统工作原理相对单一的系统,其一般是根据位置检测反馈组成闭环位置伺服系统。
其组成框图参考图1-1内容[14]。
此类系统主要原理是对比输入的目标位置信号和位置检测设备测试的真实位置信号统计其偏差且使用功率变换器的输入端弱化误差。
控制量被信号转换和功率放大驱动,驱动伺服组织,促使误差不断缩减少,一直到最佳值。
(1)位置检测装置是此类系统的关键构成方面,完整系统的动态功能是否可以满足需求,关键的是位置检测传感器的科学选择以及精度。





1.模糊控制器的输入、输出变量分别为偏差、偏差的变化率和控制量的增量。
实际论域e、ec、u[-30,30],[-24,24],[-36,36]。
对应的模糊语言变量E、EC、UC的论域均为{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}2.定义模糊子集及隶属函数对语言变量偏差E定义八个模糊集分别表示PL(正大),PM(正中),PS(正小),PZ(正零),NZ(负零),NS(负小),NM(负中),NL(负大)。
语言变量偏差的变化率EC定义七个模糊集,分别表示PL,PM,PS,Z,NS,NM,NL。
控制量的增量UC定义七个模糊集UC1,…,UC8,分别表示PL,PM,PS,Z,NS,NM,NL。
隶属度函数分别如下面3张表。
E i的隶属函数表ECi的隶属函数表UCi的隶属函数表模糊控制规则如下表试计算控制表。
计算结果如下;设已知输入为0x 和0y ,模糊化运算采用单点模糊集合,则相应的输入量模糊集合'A 和'B 分别为:()()⎩⎨⎧≠==⎩⎨⎧≠==000001,01''y y y y y x x x x x B A μμ通过模糊推理方法及性质,可求得输出量的模糊集合'C 为:()()()()[]()[]()[]561'561''561''561''561'''''=======→→=→⨯⨯=⨯=⨯=i i i iB iA i i i i i i i i i i C C C C A B C A A C B A B A B A B A C iR R首先根据书上的表2-8、2-9、2-10如上面三个表所示,建立三个矩阵A 、B 、C 分别对应三个表中的数据,为了便于计算表2-10的数据自行规定为:NB=1,NM=2,NS=3,NZ=4,PS=5,PM=6,PB=7。

模糊控制器是一种基于模糊逻辑理论的控制系统,它利用模糊集合的概念来描述模糊输入和输出,通过模糊规则和模糊推理实现对系统的控制。
模糊控制器的组成主要包括模糊化、模糊推理、解模糊和规则库四个部分,每个部分都有其独特的用途。
1. 模糊化模糊化是将系统的实际输入转化为模糊集合的过程。
在模糊控制系统中,输入往往是模糊的、不确定的,因此需要将这些模糊的输入转化为模糊集合。
模糊化的主要目的是将具体的输入转化为模糊语言值,如“很冷”、“冷”、“适中”、“热”、“很热”等,以便更好地描述系统的输入状态。
2. 模糊推理模糊推理是模糊控制器的核心部分,它用于根据模糊规则和模糊输入来得出模糊输出。
模糊推理的过程是基于一系列的模糊规则,这些规则描述了系统输入和输出之间的关系。
通过模糊推理,模糊控制器能够根据输入的模糊语言值,利用模糊规则进行推理,从而得出模糊输出的模糊语言值。
3. 解模糊解模糊是将模糊输出转化为具体的控制量的过程。
在模糊控制系统中,输出往往是模糊的语言值,需要通过解模糊将其转化为具体的控制量。
解模糊的方法有很多种,常见的方法包括最大隶属度法、加权平均法和中心平均法等。
解模糊的目的是将模糊输出转化为可以直接应用于控制系统的具体输出值。
4. 规则库规则库是模糊控制器中存储的一系列模糊规则的集合。
模糊规则描述了系统输入和输出之间的关系,它通常采用“如果…那么…”的形式来表示。
在模糊控制器中,规则库起着至关重要的作用,它包含了系统的专业知识和经验,是模糊控制器能够有效进行模糊推理的基础。
总体来说,模糊控制器的组成部分分别完成了模糊输入的转化、模糊推理的实现、模糊输出的转化和存储的模糊规则,这些部分相互协作,共同实现了对模糊、不确定系统的精确控制。
模糊控制器在工业控制、汽车控制、电力系统控制等领域有着广泛的应用,其独特的优势使其成为一种不可忽视的控制方法。
模糊控制器作为一种基于模糊逻辑理论的控制系统,在实际应用中具有诸多优势。

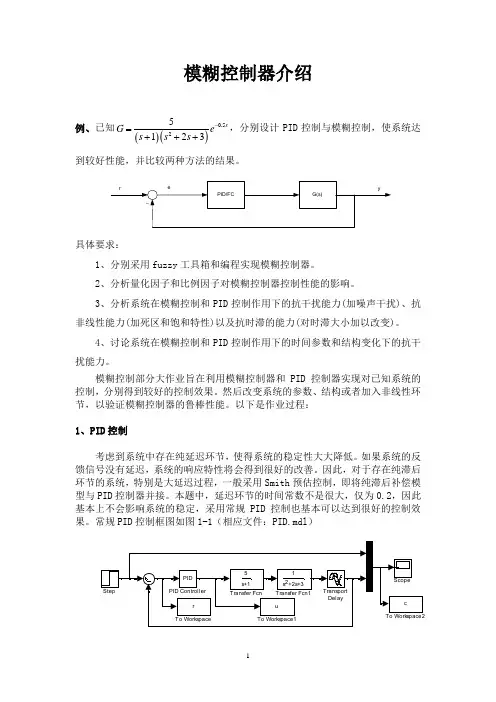
模糊控制器介绍例、已知()()0.525123s G e s s s -=+++,分别设计PID 控制与模糊控制,使系统达到较好性能,并比较两种方法的结果。
具体要求:1、分别采用fuzzy 工具箱和编程实现模糊控制器。
2、分析量化因子和比例因子对模糊控制器控制性能的影响。
3、分析系统在模糊控制和PID 控制作用下的抗干扰能力(加噪声干扰)、抗非线性能力(加死区和饱和特性)以及抗时滞的能力(对时滞大小加以改变)。
4、讨论系统在模糊控制和PID 控制作用下的时间参数和结构变化下的抗干扰能力。
模糊控制部分大作业旨在利用模糊控制器和PID 控制器实现对已知系统的控制,分别得到较好的控制效果。
然后改变系统的参数、结构或者加入非线性环节,以验证模糊控制器的鲁棒性能。
以下是作业过程:1、PID 控制考虑到系统中存在纯延迟环节,使得系统的稳定性大大降低。
如果系统的反馈信号没有延迟,系统的响应特性将会得到很好的改善。
因此,对于存在纯滞后环节的系统,特别是大延迟过程,一般采用Smith 预估控制,即将纯滞后补偿模型与PID 控制器并接。
本题中,延迟环节的时间常数不是很大,仅为0.2,因此基本上不会影响系统的稳定,采用常规PID 控制也基本可以达到很好的控制效果。
常规PID 控制框图如图1-1(相应文件:PID.mdl )图1-1 常规PID 控制框图PID 参数选取:38.0=p K ,285.0=i K ,1.0=d K 常规PID 控制的单位阶跃响应曲线:图1-2 常规PID 控制响应曲线2.模糊控制模糊控制规则(相应文件:zdh.fis )各变量论域输入变量:E :[-6 6];EC :[-6 6]; 输出变量:U :[0 7] 语言变量E : NB 、NM 、NS 、NZ 、PZ 、PS 、PM 、PB (8个) EC :NB 、NM 、NS 、ZE 、PS 、PM 、PB (7个) U : NB 、NM 、NS 、ZE 、PS 、PM 、PB (7个)。
目录摘要 (1)1 模糊控制简介 (1)1.1 模糊控制方法的研究现状 (2)1.2 模糊控制的特点 (2)1.3模糊控制的研究对象 (3)1.4模糊控制的展望 (3)2 模糊控制器的结构与工作原理 (4)2.1基本结构与组成 (4)2.2一般模糊控制器各主要环节的功能 (4)2.3隶属函数的确定原则和基本确定方法 (5)2.4模糊条件语句与模糊控制规则 (6)2.5模糊量的判决方法 (6)2.6模糊控制规则的设计和模糊化方法 (8)2.7解模糊化 (8)3 模糊控制器的设计 (9)4 关于模糊(及智能)控制理论与技术发展的思考 (11)参考文献 (12)摘要摘要:本文主要介绍了模糊控制系统的研究现状、特点,以及模糊控制器的结构与工作原理。
同时对模糊控制器的设计进行了介绍和分析,对于其基本步骤和过程进行陈述,最后就模糊(及智能)控制理论与技术发展进行总结性的思考。
关键词:模糊控制;模糊控制器;模糊量;模糊化方法引言模糊控制是近代控制理论中的一种基于语言规则与模糊推理的高级控制策略和新颖技术,它是智能控制的一个重要分支,发展迅速,应用广泛,实效显著,引人关注[13]。
随着科学技术的进步,现代工业过程日趋复杂,过程的严重非线性、不确定性、多变量、时滞、未建模动态和有界干扰,使得控制对象的精确数学模型难以建立,单一应用传统的控制理论和方法难以满足复杂控制系统的设计要求。
而模糊控制则无需知道被控对象的精确数学模型,且模糊算法能够有效地利用专家所提供的模糊信息知识,处理那些定义不完善或难以精确建模的复杂过程。
因此,模糊控制成为了近年来国内外控制界关注的热点研究领域。
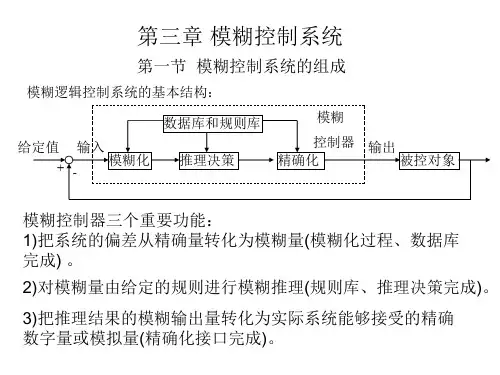
1 模糊控制简介模糊控制是一种以模糊集合论、模糊语言变量以及模糊推理为数学基础的新型计算机控制方法。
显然,模糊控制的基础是模糊数学,模糊控制的实现手段是计算机。
本章着重介绍模糊控制的基本思想、模糊控制的基本原理、模糊控制器的基本设计方法和模糊控制系统的性能分析。
实验二模糊控制实验实验目的matlab中的模糊工具箱的使用及模糊控制器的应用1)用fuzzy工具箱计算P82 2-14,要求求出控制器输出。
2)用FUZZY工具箱完成洗衣机模糊控制器设计要求求出控制器输出。
完成模糊控制决策表。
一、用fuzzy工具箱计算P82 2-14,并与手算结果对比。
实验结果如图1-1所示,图1-1题目2-14的实验结果二、用FUZZY工具箱完成洗衣机模糊控制器设计。
(1)题目分析:洗衣时间长短实际与衣物的脏污程度有关,太脏了就洗久点,不脏就可以洗快点。
人类的操作经验是由模糊的自然语言描述的,在洗衣机的调节中,人类的操作经验是:(1)“如果污泥越多,且油脂越多,洗涤时间就越长;”(2)“如果污泥适中,且油脂适中,洗涤时间就适中;”(3)“如果污泥越少,且油脂越少,洗涤时间就越短;”通过分析可以知道这实际是一个开环的控制决策过程:输入是污泥度x与油污度y,输出是洗涤时间z。
在该规则中对这些量进行衡量的是一些模糊词语,“多”、“少”、“长”、“短”。
(2)定义输入、输出模糊集将污泥x 分为3个模糊集:{SD (污泥少),MD (污泥中),LD (污泥多)} 论域:{0,50,100}将油脂分为3个模糊集:{NG (油脂少),MG (油脂中),LG (油脂多)} 论域:{0,50,100} 输出模糊集:将洗涤时间分为5个模糊集:{VS (很短),S (短),M (中等),L (长),VL (很长)}。
论域:{0,10,25,40,60} 单位s 例如:(3)建立模糊控制器求:假设当前传感器测得信息为:x0(污泥)=90,y0(油脂)=90 观察控制器的输出。
(4)建立控制决策表 x0=10,20,30,40,50,60,70,80,90,y0=10,20,30,40,50,60,70,80,90,分别取值时,控制器的输出。
(5)改变输入输出变量的模糊值、隶属度函数的曲线、解模糊的方法等,观察控制器三维图以及控制器输出, Maltlab 提供5种反模糊化方法:1.centroid :面积重心法;2.bisector :面积等分法;3.mom :最大隶属度平均法;4.som :最大隶属度取小法;5.lom :最大隶属度取大法 三、按照上述要求完成洗衣机模糊控制器设计。
1.下图1-2为洗衣机输入为[90 90]时的输出结果xD e g r e e o f m e m b e r s h ipzD e g r e e o f m e m b e r s h i p图1-2洗衣机模糊控制器输出结果2.建立控制决策表3. 改变输入输出变量的模糊值、隶属度函数的曲线、解模糊的方法等,观察控制器三维图以及控制器输出。
1)centroid:面积重心法2)bisector:面积等分法3)mom:最大隶属度平均法4)som:最大隶属度取小法5)lom:最大隶属度取大法模糊控制实验报告学院:电气与信息工程学院专业:控制理论与控制工程学号:20140201051 姓名:张延丽实验一模糊控制的理论基础实验实验目的:1 练习matlab中隶属函数程序的编写,同时学习matlab数据的表达、格式、文件格式、存盘2 学习matlab中提供的典型隶属函数及参数改变对隶属度曲线的影响3 模糊矩阵合成仿真程序的学习4 模糊推理仿真程序1隶属函数编程(1)要求自己编程求非常老,很老,比较老,有点老的隶属度函数。
clear all;close all;for k=1:1:1001x(k)=(k-1)*0.10;if x(k)>=0&x(k)<50y1(k)=0; y2(k)=0; y3(k)=0; y4(k)=0; y5(k)=0;elsey1(k)=1/(1+(1/((x(k)-50)/5)^2));y2(k)=1/(1+(1/((x(k)-50)/5)^2))^3;y3(k)=1/(1+(1/((x(k)-50)/5)^2))^2;y4(k)=1/(1+(1/((x(k)-50)/5)^2))^(0.8);y5(k)=1/(1+(1/((x(k)-50)/5)^2))^(0.2);endendhold onplot(x,y,'k');plot(x,y,'r');plot(x,y,'b');plot(x,y,'g');plot(x,y,'y');xlabel('X Years');ylabel('Degree of membership');运行结果见图1图1(2)思考题P80 2-2 写出W及V两个模糊集的隶属函数,并绘出四个仿真后的曲线。
%membership function for old peopleclear all;close all;for k=1:1:2001x(k)=(k-1)*0.10;if x(k)>=0&x(k)<50y1(k)=0;elsey1(k)=1/(1+(1/((x(k)-50)/5)^2));endendplot(x,y1,'b');xlabel('x years');ylabel('degree of membership');hold onfor k=1:1:2001x(k)=(k-1)*0.10;if x(k)>=0&x(k)<25y2(k)=1;elsey2(k)=1/(1+((x(k)-25)/5)^2);endendplot(x,y2,'g');xlabel('x years');ylabel('degree of membership');for k=1:1:2001x(k)=(k-1)*0.10;if x(k)>=0&x(k)<25y3(k)=1;elsey3(k)=1/(1+((x(k)-25)/5)^2)^2;endendplot(x,y3,'m');xlabel('x years');ylabel('degree of membership');hold onfor k=1:1:2001x(k)=(k-1)*0.10;if x(k)>=0&x(k)<25y(k)=0;else if x(k)>25&x(k)<50y4(k)=1-1/(1+((x(k)-25)/5)^2)^2;elsey4(k)=1-1/(1+(1/((x(k)-50)/5)^2))^2;endendendplot(x,y4,'r');xlabel('x years');ylabel('degree of membership');仿真结果见图2图2 3 模糊矩阵合成仿真程序(1)(P。
Q)oR;clear all;close all;P=[0.6,0.9;0.2,0.7];Q=[0.5,0.7;0.1,0.4];R=[0.2,0.3;0.7,0.7];S=[0.1,0.2;0.6,0.5];%Compound of P and Q and Rfor i=1:2for j=1:2PQ(i,j)=max(min(P(i,:),Q(:,j)'));endendfor i=1:2for j=1:2PQR(i,j)=max(min(PQ(i,:),R(:,j)'))endend结果见图3图3(2)(PUQ)。
S;clear all;close all;P=[0.6,0.9;0.2,0.7];Q=[0.5,0.7;0.1,0.4];R=[0.2,0.3;0.7,0.7];S=[0.1,0.2;0.6,0.5];for i=1:2for j=1:2PQ(i,j)=max(P(i,j),Q(i,j)')endendfor i=1:2for j=1:2PQS(i,j)=max(min(PQ(i,:),S(:,j)')) endend运行结果见图4图4(3)(PoS)U(QoS);clear all;close all;P=[0.6,0.9;0.2,0.7];Q=[0.5,0.7;0.1,0.4];R=[0.2,0.3;0.7,0.7];S=[0.1,0.2;0.6,0.5];%Compound of A and B and Cfor i=1:2for j=1:2PS(i,j)=max(min(P(i,:),S(:,j)')); endendfor i=1:2for j=1:2QS(i,j)=max(min(Q(i,:),S(:,j)')); endendfor i=1:2for j=1:2PSQS(i,j)=max(PS(i,j),QS(i,j)')endend运行结果见图5图5 4 模糊推理仿真程序思考题2-9clear allclose alla=[0.5;1;0.1]b=[0.1;1;0.6]c=[0.4;1]for i=1:3for j=1:3ab(i,j)=min(a(i),b(j));%求Dendendt1=[];for i=1:3t1=[t1;ab(i,:)'];end%求DT;for i=1:9for j=1:2r(i,j)=min(t1(i),c(j));endend%求Ra1=[1;0.5;0.1]b1=[0.1;0.5;1]for i=1:3for j=1:3ab1(i,j)=min(a1(i),b1(j)); %求D1 endendt2=[];for i=1:3t2=[t2;ab1(i,:)'];endfor i=1:9for j=1:2d(i,j)=min(t2(i),r(i,j));c1(j)=max(d(:,j))endendc1运行结果见图6图6。