当前位置：文档之家 › 模糊控制器设计实例

模糊控制器设计实例

  • 格式：ppt
  • 大小：202.50 KB
  • 文档页数：38

下载文档原格式

  / 38

合集下载

模糊控制案例001

模糊控制案例001

10) 11) 12) 13) 14) 15) 16) 17) 18) 19)
If E=Z and EC=PB or PS then U=PS If E=Z and EC=Z then U=Z If E=NS and EC=NB or NS then U=Z If E=NS and EC=Z or PS then U=PS If E=NS and EC=PB then U=PM If E=NM and EC=NB then U=PS If E=NM and EC=Z or NS then U=PM If E=NB and EC=NS or NB then U=PM If E=NM and EC=PB or PS then U=PB If E=NB and EC=Z or PS or PB then U=PB
以不是，甚至可以不是一个整数，经变
换后，是基本论域上的元素。
• 模糊控制的特点 所谓的模糊控制，既不是指被控制的 对象是模糊的，也不是模糊控制器是不确 定的，模糊控制有着自己的一套精确的理 论和算法。所谓的模糊是指在表示知识， 概念上的模糊性。虽然模糊控制器的算法 是通过模糊语言描述的，但它所完成的是 一项完全确定性的工作。
表4 模糊控制规则表格
E Ai
U Ck EC Bj
A1 PB
NM C6 R2 NB C7
A2 PM
NS C5 R4 NM C6 R5 NB C7 R3
A3 PS
Z C4 R6 NS C5 R7 NM C6 R6
A4 Z
PS C3 R10 Z C4 R11 NS C5 R9
A5 NS
PM C2 R14 PS C3 R13 Z C4 R12
A6 NM
PB C1 R18 PM C2 R16 PS C3 R15

模糊控制程序实例

模糊控制程序实例

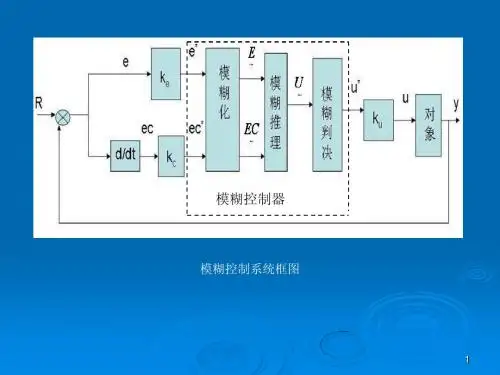
5.2.2 .6 模糊控制器设计实例1 、单输入模糊控制器的设计【例 5.12 】已知某汽温控制系统结构如图 5.10 所示，采用喷水减温进行控制。

设计单输入模糊控制器，观察定值扰动和内部扰动的控制效果。

图 5.10 单回路模糊控制系统按表 5-2 确定模糊变量 E 、 U 的隶属函数，按表 5-3 确定模糊控制规则，选择温度偏差 e 、控制量 u 的实际论域：，则可得到该系统的单输入模糊控制的仿真程序如 FC_SI_main.m 所示，仿真结果如图 5.11 所示。

设温度偏差 e 、控制量 u 的实际论域：，选择 e 、 u 的等级量论域为量化因子。

选择模糊词集为 { NB,NS,ZO,PS,PB } ，根据人的控制经验，确定等级量 E ， U 的隶属函数曲线如图 5-8 所示。

根据隶属函数曲线可以得到模糊变量 E 、 U 的赋值表如表 5-3 所示。

图5-8 E ，U 的隶属函数曲线表 5-3 模糊变量 E 、 U 的赋值表( μ )-3 -2 -1 0 1 2 3 等级量μE 、 UPB 0 0 0 0 0 0.5 1 PS 0 0 0 0 1 0.5 0 ZO 0 0 0.5 1 0.5 0 0 NS 0 0.5 1 0 0 0 0 NB 1 0.5 0 0 0 0 0依据人手动控制的一般经验，可以总结出一些控制规则，例如：若误差 E 为 O ，说明温度接近希望值，喷水阀保持不动；若误差 E 为正，说明温度低于希望值，应该减少喷水；若误差 E 为负，说明温度高于希望值，应该增加喷水。

若采用数学符号描述，可总结如下模糊控制规则：若 E 负大，则 U 正大；若 E 负小，则 U 正小；若 E 为零，则 U 为零；若 E 正小，则 U 负小；若 E 正大，则 U 负大。

写成模糊推理句 :if E =NB then U =PBif E =NS then U =PSif E=ZO then U=ZOif E =PS then U =NSif E =PB then U =NB由上述的控制规则可得到模糊控制规则表，如表 5-4 所示。

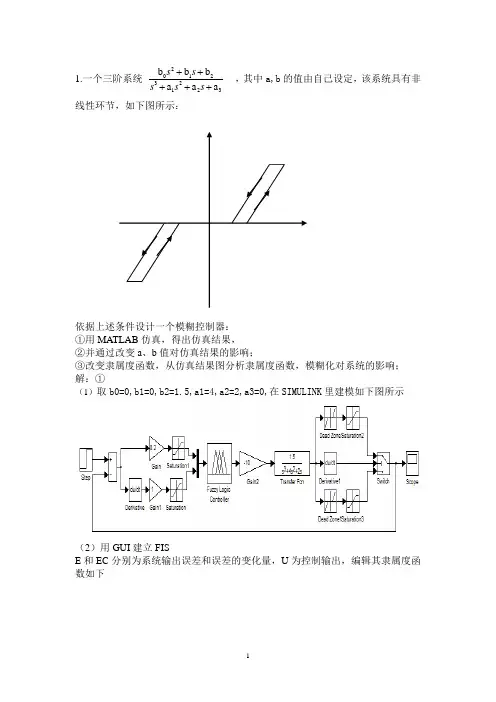
模糊控制设计及仿真实例智能控制作业

模糊控制设计及仿真实例智能控制作业

1.一个三阶系统201232123b b b a a a s s s s s +++++ ，其中a,b 的值由自己设定，该系统具有非线性环节，如下图所示：依据上述条件设计一个模糊控制器： ①用MATLAB 仿真，得出仿真结果， ②并通过改变a 、b 值对仿真结果的影响；③改变隶属度函数，从仿真结果图分析隶属度函数，模糊化对系统的影响； 解：①（1）取b0=0,b1=0,b2=1.5,a1=4,a2=2,a3=0,在SIMULINK 里建模如下图所示（2）用GUI 建立FISE 和EC 分别为系统输出误差和误差的变化量，U 为控制输出，编辑其隶属度函数如下编辑模糊推理规则如下(3)仿真结果如下2自己选定一个对象，设计一个神经网络控制系统。

解：被控对象为y(k)=0.3y(k-1)+0.2y(k-2)+0.1u(k-1)+0.6u(k-2),采用单神经元PID 控制，控制结构如下图所示：采用有监督的Hebb 学习规则，控制算法及学习算法如下：3131111222333()(1)()()()()/()()(1)()()()()(1)()()()()(1)()()()i i i i i i i I P D u k u k K w k x k w k w k w k w k w k z k u k x k w k w k z k u k x k w k w k z k u k x k ηηη=='=-+'==-+=-+=-+∑∑式中，2123()();()()(1);()()()2(1)(2);x k e k x k e k e k x k e k e k e k e k ==--=∆=--+-K K >0I P D ηηη﹑﹑分别为积分﹑比例﹑微分的学习速率，为神经元比例系数，。

输入信号为方波：()rin k 0.5sgn (sin (4t))π=仿真程序如下：clear all ; close all ;x=[0,0,0]';xiteP=0.40; xiteI=0.35; xiteD=0.40;wkp_1=0.10;wki_1=0.10;wkd_1=0.10;error_1=0;error_2=0;y_1=0;y_2=0;y_3=0;u_1=0;u_2=0;u_3=0;ts=0.001;for k=1:1:1000time(k)=k*tsrin(k)=0.5*sign(sin(4*pi*k*ts));yout(k)=0.3*y_1+0.2*y_2+0.1*u_1+0.6*u_2;error(k)=rin(k)-yout(k);wkp(k)=wkp_1+xiteP*error(k)*u_1*x(1);%Pwki(k)=wki_1+xiteI*error(k)*u_1*x(2);%Iwkd(k)=wkd_1+xiteD*error(k)*u_1*x(3);%DK=0.12;x(1)=error(k)-error_1;x(2)=error(k);x(3)=error(k)-2*error_1+error_2;wadd(k)=abs(wkp(k))+abs(wki(k))+abs(wkd(k)); w11(k)=wkp(k)/wadd(k);w22(k)=wki(k)/wadd(k);w33(k)=wkd(k)/wadd(k);w=[w11(k),w22(k),w33(k)];u(k)=u_1+K*w*x;%Control lawif u(k)>10u(k)=10;endif u(k)<-10u(k)=-10;endu_3=u_2;u_2=u_1;u_1=u(k);y_3=y_2;y_2=y_1;y_1=yout(k);wkp_1=wkp(k);wkd_1=wkd(k);wki_1=wki(k);endfigure(1);plot(time,rin,'b',time,yout,'r');xlabel('time(s)');ylabel('rin,yout'); figure(2);plot(time,error,'r');xlabel('time(s)');ylabel('error');figure(3);plot(time,u,'r');xlabel('time(s)');ylabel('u');仿真结果如下：3.前向神经网络拟合一个函数y=sin(x)*cos(10x),取n个样本，神经网络的层数和每层的点数可自定。

模糊控制器设计实例

模糊控制器设计实例

模糊控制器在智能家居中的应用
总结词
提升家居舒适度
详细描述
智能家居系统中的温度、湿度、光照等环境因素的控制可以通过模糊控制器实 现。通过将传感器采集的环境参数进行模糊化处理，根据模糊逻辑规则进行推 理，实现对家居环境的智能调节，提升家居的舒适度。
模糊控制器在智能家居中的应用
总结词：节能环保
详细描述：在智能家居中，模糊控制器能够根据家庭成员的生活习惯和环境参数，智能调节家电的运 行状态，实现节能环保。例如，根据室内外温度和光照强度，模糊控制器可以智能调节空调和照明设 备的运行状态，减少能源的浪费。
进方向。
模糊控制器性能优化
算法优化
改进模糊控制器的核心算法，提高响 应速度和控制精度。
参数调整
根据实际应用需求，调整模糊控制器 的参数，以优化控制效果。
抗干扰设计
增强模糊控制器的抗干扰能力，提高 系统的稳定性和鲁棒性。
人机交互优化
改进用户界面和操作方式，提高模糊 控制器的易用性。
05
模糊控制器发展趋势与展望
高医疗设备的安全性和可靠性。
模糊控制器在医疗设备中的应用
总结词
辅助医生诊断
VS
详细描述
在医疗影像诊断中，模糊控制器可以对医 学影像数据进行处理和分析，辅助医生进 行疾病诊断。通过对医学影像数据进行模 糊化处理，提取病变特征，并根据模糊逻 辑规则进行推理，帮助医生快速准确地判 断病情。
04
模糊控制器性能评估
02
模糊控制器设计实例
模糊控制器实例选择
实例选择
选择一个适合的模糊控制器实例，例 如温度控制器、速度控制器等，需要 考虑控制对象的特性和控制要求。
实例分析
对所选实例进行详细分析，了解其输 入输出变量、控制规则等，为后续设 计提供基础。

模糊pid控制实例

模糊pid控制实例

模糊pid控制实例以下是一个模糊PID控制的简单实例：假设我们要控制一台电机的转速，目标是使电机转速尽可能稳定在设定值附近。

根据模糊PID控制器的工作原理，我们可以进行以下步骤：1. 设定目标值和初始设定值：设定电机转速的目标值，例如1000转/分钟。

同时设置初始的PID参数。

- 设定值（SP，Set Point）= 1000 RPM- 比例增益 (Kp) = 1- 积分时间(Ti) = 1- 微分时间(Td) = 0.12. 测量电机转速：使用传感器或编码器来测量电机当前的转速，得到当前的反馈值。

3. 模糊控制规则建立：基于当前误差（设定值减去反馈值）和误差的变化率，建立一组模糊逻辑规则，例如： - 如果误差为"NB"并且误差变化率为"PB"，则输出为"NB"。

- 如果误差为"NB"并且误差变化率为"NM"，则输出为"NM"。

- ...4. 模糊推理和模糊输出：根据模糊逻辑规则，进行模糊推理，即将当前的误差和误差变化率映射到模糊输出的隶属度值上。

5. 解模糊：将模糊输出映射回具体的控制量，例如根据模糊输出计算PID控制器的输出量。

6. 更新PID参数：根据误差的变化和模糊输出的结果来更新PID控制器的参数，例如根据误差的大小和变化率来调整PID参数，以使控制更加精确。

7. 反馈控制：将PID控制器的输出量应用于电机，调整电机的转速。

8. 循环控制：循环执行上述步骤，不断更新PID参数和反馈控制，使得电机转速尽可能稳定在设定值附近。

需要注意的是，以上是一个简单的示例，实际的模糊PID控制根据具体的应用情况和系统特点会有所差异。

参数的选择和模糊规则的建立都需要根据具体的控制对象进行优化和调整。

此外，在实际应用中，还需要考虑到系统的鲁棒性、性能指标等因素。

3.3模糊控制器设计举例

3.3模糊控制器设计举例

2
模糊控制器设计方案： 一、确定模糊控制器的结构及输入、输出语言变量 采用双输入单输出的二维模糊控制器。 输入语言变量：偏差E、偏差变化率EC。 e=r-y e为偏差，r为温度设定值，y为温度测量值。 输出语言变量：可控硅触发电路中的偏置电压的变化 量U
3
模糊控制器
模糊控制系统框图
4
二、输入语言变量偏差E、偏差变化EC和输出语言 变量控制量变化U的语言值的确定
模糊控制器
模糊控制系统框图
1
3.3
模糊控制器设计举例
某电热炉用于金属零件的热处理，要求保持炉温600℃
不变。电热炉的供电电压是由可控硅整流电源提供的，它 的电压连续可调。调整可控硅触发电路中的偏置电压，即 改变可控硅的导通角时，可控硅整流电源的电压可根据需 要调整。
因为炉温受被处理零件多少、体积大小以及电网电压 波动等因素影响，难以建立精确的数学模型。因此采用模 糊控温方案。
化值 u 。
u
16
模糊控制器
模糊控制系统框图
17
模糊控制查询表
e
*
u
*
ec
*
18
以上为初步设计，需到现场调试最终确 定控制参数。 控制规则 隶属函数 量化因子
19
e* , ec* ，且 e* X {-6,-5,,-0,0,,5,6} ec* Y {-6,-5,,0,,5,6}
*
量化后得
将 e* 则
, ec
* ~
模糊化得模糊子集 E * , EC *
~ ~
U ( E EC ) R
* * ~ ~ ~
13
五、解模糊与模糊控制表的生成
-6, ..., 0, …, +6, +7 } ) 上的元素与之一一对应，

模糊控制器设计例子


负最大值 (u ) e 正最大值 (u ) e
( u 5) 2 ( u 5) 2
, 零 (u ) e ,
u2
,
应用中心平均解模糊器和乘积推理机，可以得到如下 的模糊控制器u fuzz： u fuzz x）= （ 1 1 1 1 5 5 30x 30x 1+e-30x1 1+e-30x2 1+e 1 1+e 2 1 1 1 1 1 1 1+e-30x1 1+e30x2 1+e30x1 1+e-30x2 1+e-30x1 1+e-30x2
0
1
2
Hale Waihona Puke 345 t(sec)
6
7
8
9
10
14
12
10
8
6
4
2
0 0
1
2
3
4
5 t(sec)
6
7
8
9
10
非常感谢各位同学！ 祝大家期末愉快！ 谢谢！
仿真实验：倒立摆系统的动态方程为：
x1 x2
2 mlx2 cos x1 sin x1 cos x1 g sin x1 mc m mc m x2 u 2 2 4 m cos x1 4 m cos x1 l l 3 mc m 3 mc m 其中，g =9.8m/s 2是重力加速度，mc =1kg是小车的
假设：存在可确定函数f ( x )和g L ( x)，使得
U
f ( x ) f U ( x )，0<g L ( x ) g ( x )。 即，假设 f ( x ) 的上界和g ( x )的下界是已知的。

实验二 典型模糊控制器的设计1

实验二典型模糊控制器的设计实验内容解析：实验1：（1）步骤：1.确定观测量和控制量定义理想液位O点的水位为，实际测得液位为h，液位差为e=Δh=—h2.输入量和输出量的模糊化将偏差e分为5个模糊集：负大（NB）、负小（NS）、零（Z）、正小（PS）、正大(PB)。

将偏差e的变化分为7个等级:-3，-2，-1,0,1,2,3。

控制量u为调节阀门开度的变化。

将其分为5个模糊集：负大（NB）、负小（NS）、零（Z）、正小（PS）、正大(PB)。

将u的变化分为9个模糊集：-4，-3，-2，-1,0,1,2,3,4。

3.模糊规则的描述将规则用“IF A THEN B ”的形式来描述。

4.求模糊关系（求模糊关系R）5.模糊决策模糊控制器的输出为误差向量和模糊关系的合成，即u= e o R6.控制量的反模糊化（2）设计程序如下：%Fuzzy Control for water tankclear all;close all;a= newfis('fuzz_tank');a= addvar(a,'input','e',[-3,3]); %Parameter ea= addmf(a,'input',1,'NB','zmf',[-3,-1]);a= addmf(a,'input',1,'NS','trimf',[-3,-1,1]);a= addmf(a,'input',1,'Z','trimf',[-2,0,2]);a= addmf(a,'input',1,'PS','trimf',[-1,1,3]);a= addmf(a,'input',1,'PB','smf',[1,3]);a= addvar(a,'output','u',[-4,4]); %Parameter ua= addmf(a,'output',1,'NB','zmf',[-4,-1]);a= addmf(a,'output',1,'NS','trimf',[-4,-2,1]);a= addmf(a,'output',1,'Z','trimf',[-2,0,2]);a= addmf(a,'output',1,'PS','trimf',[-1,2,4]);a= addmf(a,'output',1,'PB','smf',[1,4]);rulelist=[1 1 1 1; %Edit rule base2 2 1 1;3 3 1 1;4 4 1 1;5 5 1 1];a= addrule(a,rulelist);a1= setfis(a,'DefuzzMethod','mom'); %Defuzzywritefis(a1,'tank'); %Save to fuzzy file "tank.fis" a2= readfis('tank');figure(1);plotfis(a2);figure(2);plotmf(a2,'input',1);figure(3);plotmf(a2,'output',1);flag=1;if flag==1showrule(a2);ruleview('tank');enddisp('...............................................................');disp(' fuzzy control table:e = [-3,+3],u=[-4,+4]' ); disp('...............................................................');for i = 1:1:7e(i) = i-4;Ulist(i) = evalfis([e(i)],a2);endUlist = round(Ulist)e= -3; %Erroru= evalfis([e],a2); %Using fuzzy interference （3）实验结果：...............................................................fuzzy controller table:e = [-3,+3],ec=[-3,+3] ..............................................................................................................................fuzzy control table:e = [-3,+3],u=[-4,+4] ...............................................................Ulist =-4 -2 -2 0 2 2 4System tank: 1 inputs, 1 outputs, 5 rulese (5)-3-2-1012300.20.40.60.81eD e g r e e o f m e m b e r s h i p-4-3-2-10123400.20.40.60.81uD e g r e e o f m e m b e r s h i p实验2：（1）步骤1．模糊控制器的结构单变量二维模糊控制器是常见的结构形式。

模糊控制器设计实例


de e
模糊PD
U PD
U1
图3-15 模糊PD＋精确积分
Ki e
Ui
3）以上两种混合结构由于包含了确定性的比例环节和积分环
节，因此实质上不是纯粹的模糊PID控制器。如果将类型2）中
的分增益Ki 进行模糊化就变成了类型3）的模糊PID控制器。其
中控制器的总输出值为
U3 U PD Fuzzy(Ki ) e
PS NM NS ZE PS PM PB PB
PM NS ZE PS PM PB PB PB
PB ZE PS PM PM PB PB PB
控制值U PD
由上表可知，对于一个二维的PD控制器规则库在7个语言值条
件下共有7×7＝49条规则，如果要实现模糊PID控制器的规 则库，则需要7×7×7＝343条规则。因此入语言变量的增 加会导致规则库的迅速增加。再则，如果系统为二输入二 输出的多输入多输出系统时 其模糊PID控制器的规则库将 达到117649条。
二、常规PID参数的模糊自整定技术
要为求，了利满用足模在糊不控同制误规差则e 在和线误对差变PID化参数e 进对行PI修D正参，数便自构整成定了的
参数模糊自整正PID控制器，其控制系统的结构如下图。图略
这种技术的设计思想是先找出PID三个参数与误差 和误差变
化 之间的模糊关系，在运行中通过不断检测 和e ，再根据
PM
0
0
0
0
0
0.1 0.4 0.7 1 0.7 0.4
PS
0
0
0
0.1 0.4 0.7
1
0.7 0.4 0.1 0
ZE
0
0
0.1 0.4 0.7
1
0.7 0.4 0.1 0

模糊控制在matlab中的实例

模糊控制在matlab中的实例模糊控制是一种应用广泛的控制方法，它可以处理那些难以精确建立数学模型的系统。

在Matlab中，使用Fuzzy Logic Toolbox工具箱可以方便地实现模糊控制系统。

以下是一个简单的模糊控制器示例，控制一个小车的速度和方向，使得其能够沿着预设的轨迹行驶。

1. 首先，定义输入和输出变量。

这里我们需要控制小车的速度和转向角度。

代码如下：```speed = newfis("speed");speed = addvar(speed,"input","distance",[0 10]);speed = addmf(speed,"input",1,"slow","trimf",[0 0 5]);speed = addmf(speed,"input",1,"fast","trimf",[5 10 10]); speed = addvar(speed,"output","velocity",[-10 10]);speed = addmf(speed,"output",1,"reverse","trimf",[-10-10 -2]);speed = addmf(speed,"output",1,"stop","trimf",[-3 0 3]); speed = addmf(speed,"output",1,"forward","trimf",[2 10 10]);angle = newfis("angle");angle = addvar(angle,"input","position",[-1 1]);angle = addmf(angle,"input",1,"left","trimf",[-1 -1 0]);angle = addmf(angle,"input",1,"right","trimf",[0 1 1]); angle = addvar(angle,"output","steering",[-1 1]);angle = addmf(angle,"output",1,"hard_left","trimf",[-1 -1 -0.5]);angle = addmf(angle,"output",1,"soft_left","trimf",[-1 -0.5 0]);angle = addmf(angle,"output",1,"straight","trimf",[-0.5 0.5 0.5]);angle = addmf(angle,"output",1,"soft_right","trimf",[0 0.5 1]);angle = addmf(angle,"output",1,"hard_right","trimf",[0.5 1 1]);```2. 然后，定义模糊规则。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

⑤确定模糊关系Rl
E Ai U Ck EC Bj
A1 PB NM C6 R2 NB C7 R1
A2 PM NS C5 R4 NM C6 R5 NB C7 R3
A3 PS Z C4 R6 NS C5 R7 NM C6 R6
A4 Z PS C3 R10 Z C4 R11 NS C5 R9
A5 NS PM C2 R14 PS C3 R13 Z C4 R12
3. 确定语言值隶属度函数。对上面各语 言之给定其模糊化的隶属度函数，这 里为简单起见选择三角形函数。
B5
NB
B4
NS
B3 B2 Z PS
B1
PB
0.1 -3 -2 -1 0 (b) 1 2 3
ec Y
C7
NB
C6
NM
C5
NS
C4 C3 C2 C1 Z PS PM PB
0.1 -3 -2 -1 0 (c) 1 2 3
模糊控制技术
模糊控制器设计实例
上水箱
• 考虑 右图 液位 系统 的模 糊控 制器 设计。
V1
倒锥形容器 V2 h 下水箱 泵
测量装置
模糊控制器 操作台
p
• 受控对象：倒锥形容器的液位高度h • 检测装置：测量容器底部压力来间接测 量液位 • 执行机构：为保持液位高度h为设定值， 控制进水电磁阀V1的开启度，因此系统 V 的执行机构就是电磁阀V1 • 模糊控制器：从硬件角度看，是计算机 控制系统；从软件角度看，应设计合适 的模糊控制算法。
10) 11) Biblioteka 2) 13) 14) 15) 16) 17) 18) 19)
If E=Z and EC=PB or PS then U=PS If E=Z and EC=Z then U=Z If E=NS and EC=NB or NS then U=Z If E=NS and EC=Z or PS then U=PS If E=NS and EC=PB then U=PM If E=NM and EC=NB then U=PS If E=NM and EC=Z or NS then U=PM If E=NB and EC=NS or NB then U=PM If E=NM and EC=PB or PS then U=PB If E=NB and EC=Z or PS or PB then U=PB
② 系统液位误差前后两次采样值变化量 是ec=e2-e1=(hd-h1)-(hd-h2)=h2-h1，取 其语言变量为EC，论域Y={-3，-2，-1， 0，+1，+2，+3}，论域上的模糊子集 是Bj（j=1,2,3,…,5），相应语言值为 {正大（PB），正小（PS），零（Z）， 负小（NS），负大（NB）}。分别表 示当前水位变化h2-h1为：“快速上 升”、“上升”、“不变”、“下 降”、“快速下降”。
• 为简单起见，假设电磁阀V1的开启度与进水 量间呈线性关系。 • 注意：受控对象是倒锥形容器，其液位高度 h和进水量Q间的关系不是线性关系，且有 实质性，因此是较为复杂的控制对象。此类 控制对象采用模糊控制器是可取的方案。
1. 首先确定模糊控制器结构。为得到良 好的控制性能，观测液位误差e和误差 变化ec，控制量只有一个——电磁阀 V1的开启电压u。因此，模糊控制器采 用两输入单输出的二维结构。 2. 确定语言变量。需要确定的语言变量 有3个：误差e、误差变化ec和输出控 制电压u。
① 设液位给定高度hd，实际高度h，则液 位误差e=hd-d，取其语言变量为E，论 域X={-3，-2，-1，0，+1，+2，+3}， 论域上模糊子集是Ai(i=1,2,…,7)，相应 语言值为{正大（PB），正中（PM）， 正小（PS），零（Z），负小（NS）， 负中（NM），负大（NB）}。分别表 NM NB } 示当前水位h相对设定值hd为：“极 低”、“很低”、“偏低”、“正 好”、“偏高”、“很高”、“极 高”。
u Z
④
1) 2) 3) 4) 5) 6) 7) 8) 9)
建立模糊控制规则
If E=PB and EC=NB or NS or Z then U=NB If E=PB and EC=PB or PS then U=NM If E=PM and EC=NB or NS then U=NB If E=PM and EC=PB then U=NS If E=PM and EC=PS or Z then U=NM If E=PS and EC=NB then U=NM If E=PS and EC=NS or Z then U=NS If E=PS and EC=PB or PS then U=Z If E=Z and EC=NB or NS then U=NS
A6 NM PB C1 R18 PM C2 R16 PS C3 R15
A7 NB PB C1 R19 PM C2 R17
B1 PB B2 PS B3 Z B4 NS B5 NB
⑥ 模糊推理和解模糊
③ 系统输出控制量u，取其语言变量为U，论域 Z={-3，-2，-1，0，+1，+2，+3}，论域上 模糊子集是Ck(k=1,2,3,…,7)，相应语言值为 {正大（PB），正中（PM），正小（PS）， 零（Z），负小（NS），负中（NM），负 大（NB）}。分别表示控制执行机构动作为： “发水位高限报警，并全关闭阀门V1”、 “阀门V1开度减小量大”、“阀门V1开度减 小量小”、“阀门V1开度不变”、“阀门V1 开度增加量小”、“阀门V1开度增加量大”、 “发水位低限报警，并阀门V1开度为最大”。