下载文档原格式
第6章分离性公理§6、1 ,Hausdorff空间本节重点:掌握空间的定义及它们之间的不同与联系;掌握各空间的充要条件;熟记常见的各种空间、现在我们回到我们在第二章中提出来的什么样的拓扑空间的拓扑可以由它的某一个度量诱导出来这一问题.为了回答这个问题势必要求我们对度量空间的拓扑性质有充分的了解.读者将会发现,本章中所提到的诸分离性公理,实际上就是模仿度量空间的拓扑性质逐步建立起来的.对诸分离性的充分研究使我们在§6、5中能够对于前述问题作一个比较深刻的(虽然不就是完全的)回答.定义6.1.1 设X就是一个拓扑空间,如果X中的任意两个不相同的点中必有一个点有一个开邻域不包含另一个点(即如果x,y∈X,x≠y,则或者x有一个开邻域U使得y U,或者y有一个开邻域V使得x V),则称拓扑空间X就是一个空间.拓扑空间自然不必都就是空间,例如包含着不少于两个点的平庸空间就不就是空间.定理6.1.1 拓扑空间X就是一个空间当且仅当X中任意两个不同的单点集有不同的闭包.(即如果x,y∈X,x≠y,则.)证明充分性:设定理中的条件成立.则对于任何x,y∈X,x≠y,由于,因此或者成立,或者成立.当前者成立时,必定有.(因为否则)、这推出x有一个不包含y的开邻域.同理,当后者成立时,y有一个不包含x的开邻域.这证明X就是一个空间.必要性:设X就是一个空间.若x,y∈X,x≠y,则或者x有一个开邻域U使得或者y有一个开邻域V使得.若属前一种情形,由于,若属后一种情形,同样也有.定义6.1.2 设X就是一个拓扑空间.如果X中的任意两个不相同的点中每一个点都有一个开邻域不包含另一个点,则称拓扑空间X就是一个空间.空间当然就是空间.但反之不然.例如设X={0,1},T={,{0},X},则T就是X的一个拓扑,并且拓扑空间(X,T)就是的但不就是的.(请读者自己验证,) 定理6.1.2 设X就是一个拓扑空间,则以下条件等价:(1)X就是一个空间;(2)X中每一个单点集都就是闭集;(3)X中每一个有限子集都就是闭集.证明(1)蕴涵(2).设x∈X.当X就是一个空间时,对于任何y∈X,y≠x,点x有一个邻域U使得,即、这证明单点集{x}就是一个闭集.(2)蕴涵(3).这就是显然的、因为有限个闭集的并仍然就是闭集、(3)蕴涵(1).设x,y∈X,x≠y,当(3)成立时单点集{x}与{y}都就是闭集.从而分别就是y与x的开邻域,前者不包含x,后者不包含y.这就证明了X就是一个空间、下面的两个定理表明,空间中关于凝聚点与序列收敛的性质与我们在数学分析中熟知的多了一些类似之处.定理6.1.3 设X就是一个空间.则点x∈X就是X的子集A的一个凝聚点当且仅当x的每一个邻域U中都含有A中的无限多个点,即U∩A就是一个无限集.证明定理充分性部分就是明显的.以下证明必要性部分.假设x∈X,x∈d(A).如果x有一个开邻域U使得U∩A就是一个有限集,则集合B=U∩A-{x}也就是一个有限集,因此就是一个闭集.因此U－B就是一个开集,并且就是x的一个邻域.此外易见(U－B)∩(A-{x})=、这蕴含着x不就是A的凝聚点,与假设矛盾.定理6.1.4 设X就是一个空间.则X中的一个由有限个点构成的序列{}(即集合{|i∈Z+}就是一个有限集)收敛于点x∈X当且仅当存在N＞0使得=x对于任何i≥N成立.证明由于X就是一个空间,集合A＝{|≠x,i=1,2…}就是一个有限集,所以就是一个闭集.从而就是x的一个开邻域.于就是存在N＞0使得当i≥N有,因而=x、定义6.1.3 设X就是一个拓扑空间.如果X中任何两个不相同的点各自有一个开邻域使得这两个开邻域互不相交(即如果x,y∈X,x≠y,则点x有一个开邻域U,点y有一个开邻域V,使得U∩V=),则称拓扑空间X就是一个Hausdorff空间,或空间.hausdorff空间一定就是空间,但反之不然.例6.1.1 非Hausdorff的空间的例子.设X就是一个包含着无限多个点的有限补空间.由于X中的每一个有限子集都就是闭集,因此它就是一个空间.然而在拓扑空间X中任何两个非空的开集一定会有非空的交.这就是因为X中每一个非空开集都就是X中的有限子集的补集,而X又就是一个无限集的缘故.由此易见X必然不就是一个空间.定理6.1.5 Hausdorff空间中的任何一个收敛序列只有一个极限点.证明设{}就是Hausdorff空间X中的一个序列,并且有于就是对于j＝1,2,点有一个开邻域,使得.故存在＞O使得当i≥时有.任意选取M＞max{}.可见,这就是一个矛盾.但在空间中定理6.1.5却可以不成立.例如设拓扑空间X如例6、1、1中所述,{}就是X中的任何一个由两两不同的点构成的序列,即当i≠j时有、此时对于任何y∈X与y的任一邻域U,由于U的补集就是一个有限集,所以存在N＞0使得当i≥N时有∈U.于就是lim=y.也就就是说,序列{}收敛于X中的任何一个点.作业:P155 3.4.5、。
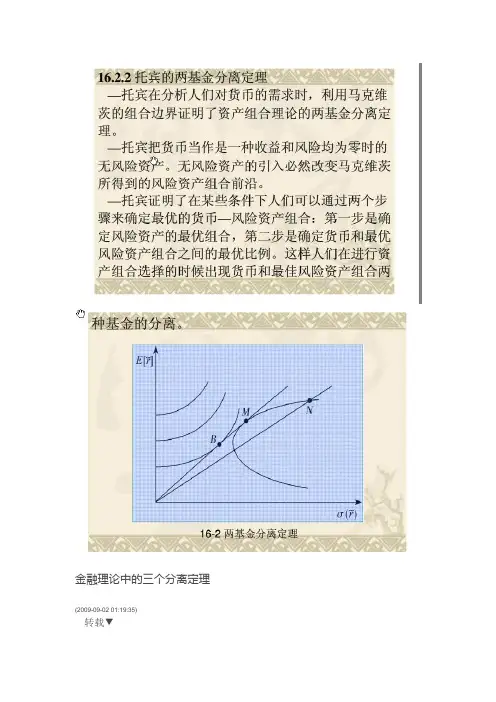
金融理论中的三个分离定理(2009-09-02 01:19:35)转载▼标签：财经分类：经济学咖啡——先天下之忧最近读文献，发现金融货币理论中有三个非常著名的分离定理（seperation theorem）,不应该混淆。
第一个是费雪的分离定理，意思是指在完全的金融市场中，生产技术的时间次序和个人的时间偏好无关。
这样，企业家可以独立的按照生产技术的时间约束来进行生产，而不用顾及消费问题，因为有完美的金融市场可以提供借贷。
第二个是托宾的分离定理，风险投资组合的选择与个人风险偏好无关。
这样基金经理就不用顾及客户的风险偏好特点，只选择最优的投资组合即可（风险既定下收益最大）。
第三个是，法玛的分离定理（两基金分离），风险投资组合的数量和构成与货币（无风险资产）无关。
这体现了法玛的“新货币经济学”思想——在经济体系中，货币是不重要的，物物交换的瓦尔拉斯世界可以在金融市场中实现。
这三个定理是非常重要的。
费雪定理告诉了人们金融市场是重要的；托宾分离告诉基金经理不要在乎客户的个人差异；法玛分离定理告诉人们货币对风险投资组合本身没有影响，并且任意投资组合都可以用一个无风险资产和风险资产组合的线性组合来表示。
▪表述：▪在均方效率曲线上任意两点的线性组合，都是具有均方效率的有效组合。
▪或：有效组合边界上任意两个不同的点代表两个不同的有效投资组合，而其他任意点均可由该两点线性组合生成▪几何含义：过两点生成一条双曲线。
▪定理的前提：两基金（有效资产组合）的期望收益是不同的，即两基金分离。
▪金融含义：若有两家基金都投资于风险资产，且经营良好(即达到有效边界)，则按一定比例投资于该两基金，可达到投资于其他基金的同样结果。
这就方便了投资者的选择。
▪CAL、CML实际上是在有风险资产组合和无风险资产组合之间又进行了一次两基金分离。
此时投资者仅需确定一个有风险组合，即可达到各种风险收益水准的组合。
资本配置更加方便。
分离定理对组合选择的启示❖若市场是有效的，由分离定理，资产组合选择问题可以分为两个独立的工作，即资本配置决策（Capital allocation decision）和资产选择决策（Asset allocation decision）。
分离定律教案高中数学
1. 理解分离定律的定义
2. 掌握分离定律的运用方法
3. 能够解决相关的数学问题
教学重点：
1. 理解分离定律的概念
2. 掌握使用分离定律解决问题的方法
教学难点：
1. 运用分离定律解决复杂的数学问题
2. 理解分离定律在代数运算中的作用
教学准备：
1. 教师准备分离定律的相关知识和例题
2. 学生准备笔记和课后习题
教学过程：
1. 引入：通过一个简单的例题引入分离定律的概念，让学生了解分离定律是什么以及它的
作用。
2. 讲解：讲解分离定律的定义和基本概念，通过示例详细说明分离定律的运用方法。
3. 练习：让学生进行练习，熟练掌握分离定律的运用技巧。
4. 拓展：给学生一些拓展问题，让他们应用所学知识解决更为复杂的问题。
5. 总结：对本节课所学内容进行总结，并强调分离定律在代数运算中的重要性。
教学评价：
1. 在课堂上观察学生的表现，及时纠正他们的错误。
2. 布置课后习题，检查学生对分离定律的掌握情况。
教学反思：
教师要不断总结教学经验，改进教学方法，使学生能够更好地理解和掌握分离定律的运用。
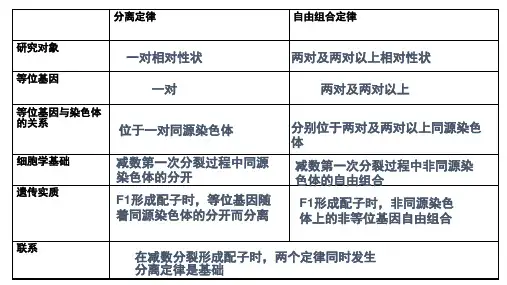
分离定律教案高中数学版
一、教学目标
1.理解分离定律的概念，掌握定律的运用方法。
2.能够灵活应用分离定律解决实际问题。
3.能够通过练习巩固分离定律的运用技巧。
二、教学重点
1.理解分离定律的概念及基本原理。
2.掌握分离定律在数学问题中的运用方法。
三、教学难点
1.理解并运用分离定律求解复杂问题。
2.能够灵活运用分离定律解决实际问题。
四、教学内容及过程安排
1.导入
通过一道简单的例题引入分离定律的概念，引导学生思考如何运用分离定律解决问题。
2.讲解
详细讲解分离定律的定义及运用步骤，通过几个实例讲解分离定律的具体运用方法。
3.练习
让学生自主进行练习，巩固分离定律的运用技巧，提高应用能力。
4.拓展
引导学生思考更复杂、更具挑战性的问题，拓展学生的思维深度。
五、教学总结
总结本节课的内容，强调分离定律的重要性和实际应用价值，激发学生学习的兴趣和积极性。
六、作业布置
布置相关作业，要求学生巩固今天所学内容，并提出问题以促进学生思考和进一步学习。
七、反馈与评价
对学生的表现进行评价，并根据学生的情况进行及时调整和反馈，帮助学生及时发现问题并改进。
两对相对性状的遗传学实验自由组合定律(类型题)班级: ___________ 姓名: ___________ 学号: ___________ 成绩: ___________ 一、应用分离定律解决自由组合问题---“分解组合法”例1、 1.正推: 依据亲本的基因型, 分析配子种类, 杂交后代的基因型、表现型种类及比例现有三种杂交组合甲为AA×Aa；乙为AABb×Aabb；丙为AABbCc×AabbCc, 求:甲亲本中的Aa, 乙亲本中的Aabb, 丙亲本中的AabbCc所产生的配子的种类（几种）分别是：甲乙丙②后代基因型种类（几种）分别是: 甲乙丙③后代表现型种类（几种）分别是: 甲乙丙④后代基因型分别为Aa、AaBb、AaBbcc的几率为: 甲乙丙规律总结：“单独处理、彼此相乘”所谓“单独处理、彼此相乘”法, 就是将多对性状, 分解为单一的相对性状然后按基因的分离规律来单独分析, 最后将各对相对性状的分析结果相乘。
其理论依据是概率理论中的乘法定理。
乘法定理是指：如某一事件的发生, 不影响另一事件发生, 则这两个事件同时发生的概率等于它们单独发生的概率的乘积。
课本案例:例1变式: a. 基因型为的个体进行测交, 后代中不会出现的基因型是（）A. B. C. D.b．（遗传遵循自由组合定律）, 其后代中能稳定遗传的占（）A. 100％B. 50％C. 25％D. 0自主完成同类题: 练习册P14 水平测试（3.4.5）素能提升（3,、4.5.7）2.倒推: 依据杂交后代表现型种类及比例, 求亲本的基因型例2、番茄紫茎（A）对绿茎（a）是显性, 缺刻叶（B）对马铃薯叶（b）是显性。
让紫茎缺刻叶亲本与绿茎缺刻叶亲本杂交, 后代植株数是：紫缺321, 紫马101, 绿缺310, 绿马107。
如果两对等位基因自由组合, 问两亲本的基因型是什么?豌豆种子子叶黄色（Y）对绿色为显性, 形状圆粒（R）对皱粒为显性, 某人用黄色圆粒和绿色圆粒进行杂交, 发现后代出现4种表现型, 对性状的统计结果如图所示, 问亲本的基因型为_________________。
