声波方程有限差分正演

声波方程有限元声波方程有限元方法是一种数值计算方法，用于模拟声波在介质中的传播和传输过程。

本文将介绍声波方程有限元方法的基本原理和应用。

声波方程是描述声波传播的方程，通常采用声压和粒子速度作为变量。

声波方程有限元方法是将声波方程离散化为有限个节点和单元，通过求解节点上的声压和粒子速度来模拟声波在空间中的传播。

声波方程有限元方法的基本原理是将连续的介质分割成有限个小单元，每个单元内部的声场可以用简单的函数进行逼近，从而将连续的声场离散化为有限个节点上的声场。

通过定义适当的边界条件和初始条件，可以建立起有限元方程组。

在声波方程有限元方法中，通常采用Galerkin方法对方程进行离散化。

Galerkin方法是将方程的解表示为一组基函数的线性组合，通过将方程两边与基函数进行内积得到离散方程。

常用的基函数包括分片线性函数和分片二次函数等。

一旦建立起有限元方程组，就可以通过求解方程组得到声波在空间中的传播。

常用的求解方法包括直接法和迭代法。

直接法是通过高斯消元法或LU分解等方法直接求解方程组，适用于规模较小的问题。

而迭代法则是通过迭代计算逼近方程组的解，适用于规模较大的问题。

声波方程有限元方法在声学领域有广泛的应用。

例如，可以用于模拟声波在海洋中的传播和反射，从而研究海洋声学现象；也可以用于模拟声波在地下中的传播和散射，从而研究地震勘探和岩石力学等问题。

声波方程有限元方法还可以用于声波在结构中的传播分析。

例如，可以用于模拟声波在建筑物中的传播和吸音效果，从而优化建筑物的声学设计；也可以用于模拟声波在机械设备中的传播和振动，从而优化机械设备的噪声控制。

声波方程有限元方法是一种重要的数值计算方法，可以用于模拟声波在介质中的传播和传输过程。

通过将声波方程离散化为有限个节点和单元，可以求解声波在空间中的传播并得到声场的分布。

声波方程有限元方法在声学领域和工程实践中有广泛的应用，对于研究声学现象和优化声学设计具有重要意义。

交错网格有限差分正演模拟的联合吸收边界胡建林;宋维琪;张建坤;邢文军;徐文会【摘要】三维声波方程交错网格有限差分正演模拟中的边界问题一直是热点问题.完全匹配层吸收边界(PML)具有较强且稳定的吸收效果,但必须具有一定的边界厚度才能吸收干净,这就增大了三维正演模拟的模型空间,即增加了运算量;Higdon边界能消除任意角度入射波的边界反射,也具有较强稳定性,但该高阶吸收边界离散化后过于复杂,而低阶时吸收效果不如PML边界.因此,基于对PML吸收层中的平面波传播规律的研究,重新推导PML最外层的Higdon吸收边界条件,得到含PML吸收系数的新的Higdon吸收边界条件.联合吸收边界不仅可使用较小厚度(相对于单纯PML边界)的PML层对分量进行衰减,而且在PML边界外层,能应用新推导的Higdon吸收边界条件对反射波进行匹配吸收.在相同吸收效果下,联合吸收边界大幅度降低了PML厚度,减小了运算量,得到精确的模拟结果.【期刊名称】《石油地球物理勘探》【年(卷),期】2018(053)005【总页数】7页(P914-920)【关键词】三维声波方程;交错网格有限差分;正演;PML边界;Higdon边界;联合吸收边界【作者】胡建林;宋维琪;张建坤;邢文军;徐文会【作者单位】中国石油大学(华东)地球科学与技术学院,山东青岛266555;中国石油大学(华东)地球科学与技术学院,山东青岛266555;中国石油冀东油田公司勘探开发研究院,河北唐山063004;中国石油冀东油田公司勘探开发研究院,河北唐山063004;中国石油冀东油田公司勘探开发研究院,河北唐山063004【正文语种】中文【中图分类】P6311 引言复杂地下介质中，地震波的传播过程繁冗，难以得到解析解，因此，一般是通过正演模拟探究地下地震波的传播。

在地震波正演模拟中，利用波动方程的正演模拟比用运动学的射线追踪法可获得更丰富的动力学信息，因此地震波场的数值模拟是地震波场传播研究中的重要手段之一[1-8]。

有限差分波动方程正演模拟中的吸收边界条件王开燕1，周妍1，刘丹1，郝菲2【摘要】在地震波传播的数值模拟过程中，在有限的区域内建立吸收边界条件是一个很重要的问题。

主要运用有限差分的方法对二维声波方程进行正演模拟，介绍并分析了利用有限差分的方法进行波动方程正演模拟过程中的几种吸收边界条件。

先通过理论阐述，然后通过建立均质模型和层状介质模型来研究不同吸收边界条件下的边界吸收效果，得到对应的波场快照和单炮记录，并加以比较。

通过实际验证得知当运用完全匹配层(PML)吸收边界条件时吸收效果最好，基本上不产生虚假反射。

【期刊名称】当代化工【年(卷),期】2014(000)005【总页数】4【关键词】关键词：有限差分法；正演模拟；吸收边界条件；二维声波方程；虚假反射模拟与计算地震数值模拟是地震勘探和地震学的重要基础，并已经在地震勘探和天然地震勘探中得到广泛的应用。

地震勘探过程中，我们只能得到地表和地下很少部分的数据，不可能得到波场的全部信息，只能通过波场正演模拟来获得波场的全部信息，从而全面地反映地震波在地下介质中的分布与传播情况。

地震数值模拟[1]是在已知地下介质结构情况下，研究地震波在地下各种介质中传播规律的一种地震模拟方法，其理论基础就是表征地震波在地下各种介质中传播的地震波传播理论。

本文主要采用有限差分的方法进行正演模拟[2]，但实际地震波是在无限介质中传播的，由于受计算机内存和计算时间的限制，有限差分法只能得到有限数量网格点上的波场值，所有就必须截断计算空间并设置边界条件，得到有限的计算模型，所以边界吸收条件就非常重要，如果处理不好就会产生虚假反射，影响得到的结论。

近年来，国内外许多学者在吸收边界条件方面做了大量的工作，提出了各种边界条件[3-6]。

本文通过声波方程有限差分方法，验证不同吸收边界条件下的正演模拟效果，优选出效果好的吸收边界条件。

1 二维声波方程二阶精度有限差分算法二维声波波动方程的表达式为:其中：c—声波波速；u（x，z，t）—声波波场值；f（x，z，t）—震源项。

高精度傅里叶有限差分法模型正演刘文革 3 ① 贺振华 ①② 黄德济 ① 杜增利 ③( ①成都理工大学信息工程学院 ; ②成都理工大学“油气藏地质与开发工程”国家重点实验室 ; ③西南石油大学)刘文革 ,贺振华 , 黄 德 济 , 杜 增 利 . 高 精 度 傅 里 叶 有 限 差 分 法 模 型 正 演 . 石 油 地 球 物 理 勘 探 , 2007 , 42( 6 ) : 629～633摘要 波动方程数值模拟方法分为有限差分法和频率 —波数域法两类 ,其中有限差分法的计算精度取决于波场外推算子的近似程度 、离散网格间距及差分方程阶数 ,它能适应速度任意横向变化 ,但在大倾角处易出现频 散现象及背景噪声 。

频率 —波数域法算法简单 、精度高 、噪声小 ,能适应任意地层倾角情况 ,但不适于速度场的 任意横向变化 。

文中结合有限差分法和频率 —波数域法的优点 ,应用傅里叶有限差分法 ( F F D) 实现在多域用高 精度延拓算子对模型进行地震记录的数值模拟 ,其波场外推算子由相移项 、折射项 ( 时移项) 和有限差分补偿项 组成 。

对 F F D 法进行了理论与误差分析 ,并用单程声波方程分别进行了层状模型和 SE G / EA GE 盐丘模型的数 值模拟试验 。

数值试验的对比分析表明 , F F D 法适用于速度场横向剧烈变化情形 ,且具有精度高 、无频散 、背景 噪声弱等优点 ,模拟结果反射特征清楚 ,能对复杂地质构造进行准确的地震数值模拟 。

关键词 波动方程 地震数值模拟 有限差分法 频率 —波数域法 傅里叶有限差分法提高微分方程对单平方根算子的逼近程度 ,改善了 成像效果[ 3 ]; C lae r b o u t 在研究时 —空域和频率 —空间域中的有限差分法后 ,认为有限差分法可以适应横向速度的任意变化 ,但是单平方根算子展开引起 了高波数近似 ,使得对大倾角构造的成像误差较大 , 易出现频散现象及背景噪声[ 4 ] 。

有限差分法地震正演模拟程序一．二阶公式推导1．二维的弹性波动方程22222222x x x ZU U U U t x z x z λμμλμρρρ∂∂∂∂++=++∂∂∂∂∂ 22222222xz z z U U U U t z x x zλμμλμρρρ∂∂∂∂++=++∂∂∂∂∂ 2．对方程进行中间差分（1）首先对时间进行二阶差分()()()()()112,,,22222n n n xi k xi k xi kx x x x U U U U t t U t U t t U t t t +--++-+-∂==∂ ()()()()()112,,,22222n n n zi k zi k zi kz z z z U U U U t t U t U t t U t t t +--++-+-∂==∂ （2）对x 方向进行二阶差分()()()()()21,,1,22222n n n xi k xi k xi kx x x x U U U U x x U x U x x U x x x +--++-+-∂==∂ ()()()()()21,,1,22222n n n zi k zi k zi kz z z z U U U U x x U x U x x U x x x +--++-+-∂==∂ （3）对z 方向进行二阶差分()()()()()2,1,,122222n n nxi k xi k xi k x x x x U U U U z z U z U z z U z z z +--++-+-∂==∂ ()()()()()2,1,,122222n n nzi k zi k zi k z z z z U U U U z z U z U z z U z z z +--++-+-∂==∂ （4）对xz 进行差分2,1,11,11,11,11,111,11,11,11,122224n nzi k zi k z zn n n nzi k zi k zi k zi k n n n n zi k zi k zi k zi k U U U U x z x zx z U U U U U U U U x x z z x+-++-++--++-++---⎛⎫-∂∂∂∂⎛⎫== ⎪ ⎪ ⎪∂∂∂∂∂⎝⎭⎝⎭-----+==2,1,11,11,11,11,111,11,11,11,122224n nxi k xi k x x n n n n xi k xi k xi k xi k n n n n xi k xi k xi k xi k U U U U x z x z x z U U U U U U U U x x z z x+-++-++--++-++---⎛⎫-∂∂∂∂⎛⎫== ⎪ ⎪ ⎪∂∂∂∂∂⎝⎭⎝⎭-----+==（5）把（1）（2）（3）（4）得到的结果带入波动方程3．写出差分方程()()()11,,,1,,1,22,1,,11,11,11,11,12222=2++4n n n n n nxi k xi k xi kxi k xi k xi k nnnnnnnxi k xi k xi k zi k zi k zi k zi k U U U U U U t x U U UU UUUz xz λμρμλμρρ+-+-+-++-++----+-++-+--++()()()11,,,1,,1,22,1,,11,11,11,11,12222=2++4n n n nnnzi k zi k zi kzi k zi k zi knn n nnnnzi k zi k zi k xi k xi k xi k xi k U U U U U U t x U UUU UUUz xz λμρμλμρρ+-+-+-++-++----+-++-+--++即得到()()1,,1,,1,,122112,,,1,11,11,11,1222+=2-++4n n n n n nxi k xi k xi kxi k xi k xi k n n n xi k xi k xi k n n n nzi k zi k zi k zi k U U U U U U x z U U U t U U U U z x λμμρρλμρ+-+-+-++-++---⎛⎫-+-++ ⎪ ⎪ ⎪--++ ⎪ ⎪⎝⎭()()1,,1,,1,,122112,,,1,11,11,11,1222+=2-++4n n n n n nzi k zi k zi k zi k zi k zi k n n n zi k zi k zi k n n n nxi k xi k xi k xi k U U U U U U x z U U U t U U U U z x λμμρρλμρ+-+-+-++-++---⎛⎫-+-++ ⎪ ⎪ ⎪--++ ⎪ ⎪⎝⎭二．MATLAB 程序 clear; clc;Nx=200; Nz=300;fi=30;%%%主频t_step=300;%%%%时间采样点dx=10.0;%空间采样间隔——x 方向 dz=10.0;%空间采样间隔——z 方向 dt=0.001;%时间采样间隔——1mslambda=66*1e9;%砂岩拉梅常数lamdamu=44*1e9;%砂岩拉梅常数murho=2650;%砂岩密度%%%%%%模型扩展%%%%%vp=zeros(Nz+2,Nx+2);%纵波速度vs=zeros(Nz+2,Nx+2);%横波速度c=zeros(Nz+2,Nx+2);%交叉项系数for i=1:Nz+2for j=1:Nx+2vp(i,j)=sqrt((lambda+2*mu)/rho);vs(i,j)=sqrt((mu)/rho);c(i,j)=sqrt((lambda+mu)/rho);endend%%%%%% 震源%%%%%%%t_wavelet=[1:t_step]*dt-1.0/fi;source=((1-2*(pi*fi*t_wavelet).^2).*exp(-(pi*fi*t_wavelet).^2));% 雷克子波amp=sqrt(2.0);% 振幅source_x=floor(Nx/2)+1;% 震源位置——x坐标source_z=2;% 震源位置——z坐标source_amp=zeros(Nz+2,Nx+2);% 震源振幅初始化（所有点处均为0）source_amp(source_z,source_x)=amp;% 震源振幅，在位置source_z,source_x处振幅为amp，其它位置为0 %%%%%%%%%%%%%%%%%%%%%%%%%%%U=zeros(Nz,Nx);% 弹性波x分量V=zeros(Nz,Nx);% 弹性波z分量U0=zeros(Nz+2,Nx+2);% 前一时刻的UU1=zeros(Nz+2,Nx+2);% 当前时刻的UU2=zeros(Nz+2,Nx+2);% 下一时刻的UV0=zeros(Nz+2,Nx+2);% 前一时刻的VV1=zeros(Nz+2,Nx+2);% 当前时刻的VV2=zeros(Nz+2,Nx+2);% 下一时刻的Vrecord_u=zeros(t_step,Nx);% x方向接收到的地震记录——Urecord_v=zeros(t_step,Nx);% x方向接收到的地震记录——V%%%%%% 有限差分计算U V %%%%%%for it=1:t_stepfor x=2:Nx+1for z=2:Nz+1U2(z,x)=2*U1(z,x)-U0(z,x)+(dt*dt)*(vp(z,x)^2*(1.0/(dx*dx))*(U1(z,x+1)-2*U1(z,x) +U1(z,x-1))+vs(z,x)^2*(1.0/(dz*dz))*(U1(z+1,x)-2*U1(z,x)+U1(z-1,x))+c(z,x)^2*(1. 0/(4*dx*dz))*(V1(z+1,x+1)-V1(z+1,x-1)-V1(z-1,x+1)+V1(z-1,x-1)))+source(it)*sour ce_amp(z,x)*dt*dt;V2(z,x)=2*V1(z,x)-V0(z,x)+(dt*dt)*(vs(z,x)^2*(1.0/(dx*dx))*(V1(z,x+1)-2*V1(z,x) +V1(z,x-1))+vp(z,x)^2*(1.0/(dz*dz))*(V1(z+1,x)-2*V1(z,x)+V1(z-1,x))+c(z,x)^2*(1. 0/(4*dx*dz))*(U1(z+1,x+1)-U1(z+1,x-1)-U1(z-1,x+1)+U1(z-1,x-1)));endendU0=U1;U1=U2;V0=V1;V1=V2;record_u(it,:)=U2(2,[2:201]);record_v(it,:)=V2(2,[2:201]);U=U2(2:301,2:201);V=V2(2:301,2:201);end%%%%% 绘制U 和V 的波场图%%%%%%figureimagesc(U(1:300,1:200));title('U');xlabel('x');ylabel('z');figureimagesc(V(1:300,1:200));title('V');xlabel('x');ylabel('z');%%%%% 绘制U 和V 的地震记录%%%%%%figureimagesc(record_u(1:300,1:200));title('U');xlabel('x');ylabel('t_step');figureimagesc(record_v(1:300,1:200));title('V');xlabel('x');ylabel('t_step');U分量波场图V分量波场图U分量地震记录V分量地震记录。

波动方程有限差分一、引言波动方程是自然界中许多现象的数学模型，如声波、地震波等。

为了解决波动方程的数值解，有限差分方法是一种常用的数值计算方法。

本文将详细介绍波动方程有限差分的原理、方法和应用。

二、波动方程波动方程描述了介质中物理量随时间和空间变化的规律。

具体来说，假设介质中某个物理量为u(x, t)，其中x表示空间坐标，t表示时间，则波动方程可以表示为：∂²u/∂t² = c²∇²u其中c表示介质中的传播速度，∇²表示拉普拉斯算子。

该方程描述了一个在介质中传播的二阶偏微分方程。

三、有限差分方法有限差分方法是一种常用的数值计算方法，其基本思想是将连续函数离散化为离散点上的函数值，并通过差商逼近导数或偏导数，从而得到原问题的近似解。

对于波动方程，在空间上进行网格剖分，并在每个网格点处离散化u(x, t)和其导数，可以得到如下形式的差分格式：(u(i, j+1) - 2u(i, j) + u(i, j-1)) / Δt² = c²((u(i+1, j) - 2u(i, j) + u(i-1, j)) / Δx² + (u(i, j+1) - 2u(i, j) + u(i, j-1)) / Δy²)其中i表示空间网格点的横坐标，j表示纵坐标，Δt、Δx和Δy分别为时间和空间上的步长。

这个差分方程可以通过迭代求解得到波动方程的数值解。

具体来说，可以使用显式差分法或隐式差分法进行求解。

四、应用波动方程有限差分方法在地震勘探、声学建模等领域得到广泛应用。

例如，在地震勘探中，可以通过模拟地震波传播过程得到地下岩层的结构信息；在声学建模中，可以计算音场传播过程，并预测噪声污染等问题。

五、总结本文介绍了波动方程有限差分方法的原理、方法和应用。

有限差分方法是一种常用的数值计算方法，在许多领域都有广泛应用。

对于波动方程这类偏微分方程，有限差分方法是一种有效的求解方法。

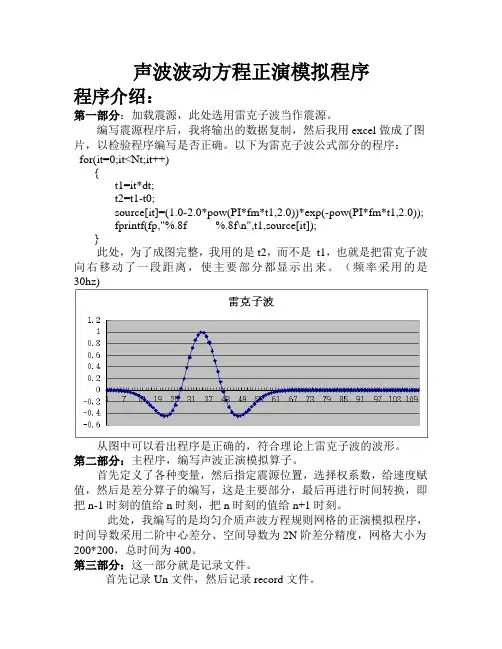
声波波动方程正演模拟程序程序介绍：第一部分：加载震源，此处选用雷克子波当作震源。

编写震源程序后，我将输出的数据复制，然后我用excel做成了图片，以检验程序编写是否正确。

以下为雷克子波公式部分的程序：for(it=0;it<Nt;it++){t1=it*dt;t2=t1-t0;source[it]=(1.0-2.0*pow(PI*fm*t1,2.0))*exp(-pow(PI*fm*t1,2.0));fprintf(fp,"%.8f %.8f\n",t1,source[it]);}此处，为了成图完整，我用的是t2，而不是t1，也就是把雷克子波向右移动了一段距离，使主要部分都显示出来。

（频率采用的是30hz)从图中可以看出程序是正确的，符合理论上雷克子波的波形。

第二部分：主程序，编写声波正演模拟算子。

首先定义了各种变量，然后指定震源位置，选择权系数，给速度赋值，然后是差分算子的编写，这是主要部分，最后再进行时间转换，即把n-1时刻的值给n时刻，把n时刻的值给n+1时刻。

此处，我编写的是均匀介质声波方程规则网格的正演模拟程序，时间导数采用二阶中心差分、空间导数为2N阶差分精度，网格大小为200*200，总时间为400。

第三部分：这一部分就是记录文件。

首先记录Un文件，然后记录record文件。

模型构建与试算：1、我首先建立了一个均匀介质模型，首先利用不同时间，进行了数值模拟，得到波场快照如图所示：100ms 200ms 300ms此处，纵波速度为v=3000m/s。

模型大小为200×200，空间采样间隔为dx=dz=10m。

采用30Hz的雷克子波作为震源子波，时间采样间隔为1ms，图中可以看出，波场快照中的同相轴是圆形的，说明在均匀各向同性介质中，点源激发的波前面是一个圆，这与理论也是吻合的。

并且随着时间的增大，波前面的面积逐渐增大，说明地震波从震源中心向外传播。

傅里叶变换法是利用空间的全部信息对波场函数 进行三角函数插值，能更加精确地模拟地震波的传播 规律，同时，利用快速傅里叶变换(FFT)进行计算，还 可以提高运算效率，其主要优点是精度高，占用内存 小，但缺点是计算速度较慢，对模型的适用性差，尤 其是不适应于速度横向变化剧烈的模型。
波动方程有限元法的做法是：将变分法用于单元分 析，得到单元矩阵，然后将单元矩阵总体求和得到总体 矩阵，最后求解总体矩阵得到波动方程的数值解；其主 要优点是理论上可适宜于任意地质体形态的模型，保证 复杂地层形态模拟的逼真性，达到很高的计算精度，但 有限元法的主要问题是占用内存和运算量均较大，不适 用于大规模模拟，因此该方法在地震波勘探中尚未得到 广泛地应用。
i 1, i, j 2 j 2
i 2, j2
x
图4-1 差分网格划分示意图
网格间隔长度
h
时间采，样步长
t
x ih
z jh
t kt
uk
uk i, j
i, j
表示(i,j)点k时刻的波场值
时间二阶、空间二阶差分格式推导如下：
将 uik,在j1 (i,j)点k时刻用Taylor展式展开：
u k 1 i, j
(4-8)
s(k为) 震源函数，
一般使用一个理论的雷克型子波代替，即：
e s(t) (2f / )2t2 cos 2ft
t 为时间
f 为中心频率，一般取为20-40HZ
为控制频带宽度的参数，一般取2-5
(i i0 ) * ( j j0 ) 确定震源位置
4.1 稳定性条件
对于特定的偏微分方程只有特定的几种有限差分 格式是无条件或有条件稳定的，（4-7）、（4-8）式即 是已被证明的有条件稳定格式，其稳定性条件分别为：

二维声波方程有限差分求解1. 引言声波方程是描述声波传播的基本方程之一，它在许多领域中都有重要的应用，如声学、地震学和无损检测等。

有限差分法是一种常用的数值求解方法，可以将连续的偏微分方程转化为离散形式进行计算。

本文将介绍二维声波方程的有限差分求解方法，并给出相应的代码实现。

2. 二维声波方程模型二维声波方程可以表示为：)其中，u是声压场强度，t是时间，x和y是空间坐标，c是介质中的声速。

为了进行数值求解，我们需要将上述偏微分方程转化为离散形式。

3. 有限差分离散化为了将二维声波方程离散化，我们可以使用中心差分法。

将时间和空间坐标分别离散化，可以得到如下的差分方程：)其中，是时间步长，和是空间步长。

根据初始条件和边界条件，我们可以使用上述差分方程进行迭代计算，从而得到声波场在不同时间步的数值解。

4. 代码实现下面给出使用Python编写的二维声波方程有限差分求解的代码示例：import numpy as npimport matplotlib.pyplot as plt# 参数设置c = 343 # 声速L = 1 # 空间长度T = 1 # 总时间Nx = 100 # 空间网格数Nt = 1000 # 时间步数dx = L / Nx # 空间步长dt = T / Nt # 时间步长# 初始化声压场矩阵u = np.zeros((Nx+1, Nx+1))u_prev = np.zeros((Nx+1, Nx+1))# 初始条件：声压场在t=0时刻为正弦波形状x = np.linspace(0, L, Nx+1)y = np.linspace(0, L, Nx+1)X, Y = np.meshgrid(x, y)u_prev[:,:] = np.sin(X*np.pi/L) * np.sin(Y*np.pi/L)# 迭代计算声压场的数值解for n in range(1, Nt+1):for i in range(1, Nx):for j in range(1, Nx):u[i,j] = (2*(1-c**2*dt**2/dx**2)*(u_prev[i,j]) - u[i,j]) + (c**2*d t**2/dx**2) * (u_prev[i-1,j] + u_prev[i+1,j] + u_prev[i,j-1] + u_prev[i,j+1])# 边界条件：固定边界上的声压为零（反射边界）u[0,:] = 0u[Nx,:] = 0u[:,0] = 0u[:,Nx] = 0# 更新声压场矩阵u_prev[:,:] = u# 绘制声波场的数值解plt.imshow(u, cmap='hot', origin='lower', extent=[0, L, 0, L])plt.colorbar()plt.xlabel('x')plt.ylabel('y')plt.title('Numerical Solution of 2D Acoustic Wave Equation')plt.show()5. 结果与讨论运行上述代码，我们可以得到二维声波方程的数值解。

三维波动方程有限差分正演方法三维波动方程有限差分正演方法是地球物理勘探领域中常用的数值计算方法之一，其主要应用于地震波传播与反演等领域。

一、三维波动方程有限差分正演方法原理三维波动方程的一般形式可以表示为：\[ \frac{\partial^2 p}{\partial t^2} = \nabla^2 p +f(x,y,z,t) \]其中$p$表示波场，$f(x,y,z,t)$表示源项函数，$\nabla^2$表示拉普拉斯算子。

对于三维波动方程的有限差分正演方法，其基本的数值离散形式如下：\[ \frac{p_{i,j,k}^{n+1} - 2p_{i,j,k}^n + p_{i,j,k}^{n-1}}{\Delta t^2} = c_x^2 \frac{p_{i+1,j,k}^n - 2p_{i,j,k}^n + p_{i-1,j,k}^n}{\Delta x^2} + c_y^2 \frac{p_{i,j+1,k}^n -2p_{i,j,k}^n + p_{i,j-1,k}^n}{\Delta y^2} + c_z^2\frac{p_{i,j,k+1}^n - 2p_{i,j,k}^n + p_{i,j,k-1}^n}{\Delta z^2} + f_{i,j,k}^n \]其中$p_{i,j,k}^n$表示波场在离散网格点$(i,j,k)$处的值，$\Delta t,\Delta x,\Delta y,\Delta z$分别表示时间和空间的离散步长，$c_x,c_y,c_z$分别表示波速在$x,y,z$方向上的离散形式，$f_{i,j,k}^n$表示源项在离散网格点$(i,j,k)$处的值。

该有限差分正演方法可以通过迭代求解，即根据当前时刻$t^n$的波场值$p_{i,j,k}^n$，计算当前时刻$t^{n+1}$的波场值$p_{i,j,k}^{n+1}$。

在迭代过程中，需要进行边界条件处理和源项的更新等操作，以确保该方法的数值计算精度和稳定性。

2P
x2
1 x2
[
5 2
Pn i, j,k
4 3
P P n i 1, j,k
n i 1, j,k
1 12
P P n i2, j,k
n i2, j,k
]
2P y2
1 y2
[
5 2
Pn i, j,k
4 3
P P n i, j 1,k
n i, j 1,k
1 12
P P n i, j 2,k
u(xΒιβλιοθήκη a)a2 2!2u x2
a4 4!
4u x4
(n为偶数)
an n!
nu xn
o(an )
（2-4）
二、声波方程的差分近似
（2-4）中分别取 a x a 2 x a 3 x
并做 o(a6 ) 误差截断得：
u(x x) 2u(x) u(x x) x2 2u x4 4u x6 6u
用类似的方法可以求得
2u 的四阶误差截断表达式：
x2
2u
x2
1 x2
{
5 2
u(x)
4 3
u(x
x) u(x
x) 1 u(x 2
12
x) u(x 2
x)}
2u 的二阶误差截断表达式：
x2
（2-8） （2-9）
2u
x2
1 x
2
u
(
x
x) 2u(x) u(x x)
（2-10）
二、声波方程的差分近似
2u x2
b1 x2
1 x2
3r1
3 10
r2
1 45
r3
二、声波方程的差分近似
2u

三维波动方程有限差分正演方法
首先，将三维波动方程进行离散化处理，将连续的空间和时间域离散
为网格点的集合。

在空间域中，将地下介质划分为多个均匀网格，每个网
格点上对应一个地震波场的值。

在时间轴上，将时间域离散为多个时间步长，每个时间步长表示一个时刻。

然后，利用有限差分算子将三维波动方程转化为离散形式。

常用的有
限差分格式有常系数差分格式和变系数差分格式。

常系数差分格式适用于
各向同性介质，而变系数差分格式适用于各向异性介质。

在三维波动方程有限差分正演方法中，需要考虑各向异性介质的模型。

各向异性介质与各向同性介质不同，其波速和波阻抗在不同方向上具有不
同的值。

因此，在离散化过程中，需要引入特殊的差分算子来考虑各向异
性的影响。

最后，利用迭代求解的方法，按时间步长依次求解离散化的波动方程。

利用差分算子和初始条件，根据时空的变化逐步更新波场的数值，并计算
出每个网格点的波动值。

通过不断迭代求解，最终可以得到地震波在地下
的传播和反射结果。

三维波动方程有限差分正演方法在地震勘探中具有重要的应用价值。

它可以模拟地震波在地下介质中的传播和反射过程，帮助研究人员了解地
下结构、油气储层等。

同时，它也可以用来研究地震波在各向异性介质中
的传播规律，提高地震勘探的准确性和效率。

总之，三维波动方程有限差分正演方法是一种常用的数值模拟方法，
可以用来模拟地震波在地下介质中的传播和反射。

它具有广泛的应用价值，对地震勘探、岩石物理、地质测井等领域具有重要的意义。

择 和适 当的数 学方法 予 以减 小 。
１２ 波动 方程 的高 阶差分 近似 ．
在做 有限 差分波 动方程 正演 数值模 拟 时主要 是 要综 合考 虑差 分格式 、 震源 的选择 、 边界 条件 的处 理
一 △ ） 开有 ｆ 展
电
０ ，
利用 泰勒公 式将 函数 （ ） ｔ 在 （ ＋△ ） ｔ ｆ 和 （ 一 ｔ
６ 。 ，。 ｘ
，
，
ｙ
，
ｚ
＝：
．
。
｛ 。 ：
动 方程 时 ， 常会产 生 不 期望 的数 值 频散 或 称 网格 常 频散 ， 导致 数值 模 拟结 果 分 辨 率 的降 低 。所谓 数值
频散 实质 上是 一种 因离散化求 解 波动方 程而 产生 的 伪 波动 ， 它是有 限差 分 方 法求 解 波 动 方程 时 所 固 有
０ ｕ １ Ｚ （ ０ ｕ ０（１ ）＋ ０（１ ）＝ Ｏｕ＋６
ｐ ｐ
㈩ （） ２ ｆ（ Ａ
ｆ ）。 （） １
取 到展开 式 的二阶项 ， 令式 （ ）＋ （ ） 到二 阶有 ３ 式 ４得
限差 分计 算公式
，ｆ ： ，） （ （ｔ Ａ） 。（ ） ８
假设 物质 的密 度不 随空 间变化 ， 方程 可表示 为 则
（． １ 东华理 工学 院 ， 西 抚 州 ３４ ０ ； ． 江 ４ ００ ２ 中南大 学 ， 南 长 沙 湖
湖南 长沙 ４０ １） １０ １
４０ ８ ； ． 南 省核 工 业地 质局 ， １０ ３ ３ 湖
摘 要： 有限差分波动方 程正演数值模拟 主要是解决差分格 式 、 震源选 择 、 边界 条件处 理等 问题 。这些 问题 的合 理 解决对得到正确和准确的波动方程数值解 有着 十分 重要 的作 用。笔者通 过对波动 方程计算 机有 限差 分正演模拟 过程的叙 述 ， 分析了在做正演模 拟时的误差来源 以及 如何有效地减小误差 。

波动方程正演模型及应用吴清岭　张　平　施泽龙3(大庆石油管理局勘探开发研究院)摘　要　地震资料解释经常用到正演模型。

常规的褶积模型不能模拟地震波的动力学特征。

本文采用声波方程,通过四阶有限差分近似,实现了复杂地质构造零炮检距的数值模拟。

文中同时展示了实际应用效果。

　主题词　正演模型 有限差分 零炮检距剖面作者简介　吴清岭,男,1962年生,1983年毕业于华东石油学院勘探系,硕士,高级工程师,现从事地震方法研究工作。

地址:(163712)黑龙江省大庆市让胡路区勘探开发研究院。

3　参加本工作的还有杨有林同志。

在地震资料解释中,人们力图得到能够保持地震波的运动学与动力学特征的波动方程正演模型,以达到精确模拟地震波传播特性的目的。

在求解波动方程的2种数值解法(有限差分法和有限元法)中,有限差分法是一种快速有效的方法,并且地质模型的复杂程度不影响运算速度。

本文介绍了对声波方程采用四阶有限差分近似制作零炮检距剖面的基本过程及应用效果。

一、基本原理1,计算公式在二维空间域内,二维声波方程为1C 292u 9t 2=92u 9x 2+92u9z 2式中　C ———声学介质下地震波的纵波速度;u ———声压。

设Δh 为空间采样步长;Δt 为时间采样步长;m 、n 、l 分别为正整数;则有x =m ・Δh z =n ・Δh t =l ・Δt 对时间域采用二阶有限差分;对空间域采用四阶有限差分(推导过程略),其数值计算公式为u (m ,n ,l +1)=(A 2/12){16[u (m +1,n ,l )+u (m -1,n ,l )+u (m ,n +1,l )+u (m ,n -1,l )]-[u (m +2,n ,l )+u (m -2,n ,l )+u (m ,n +2,l )+u (m ,n -2,l )]}+(2-5A 2)[u (m ,n ,l )-u (m ,n ,l -1)]其中 A 2=C 2(m ,n )Δt 2/Δh 2式中　C (m ,n )———介质速度的空间离散值;Δt ———时间离散步长;Δh ———空间离散步长。

有限差分法不同边界条件下的数值模拟文章介绍了地震数据处理中所使用的数值模拟法，对采用有限差分法所使用不同边界条件处理方式进行了数值模拟，通过波场快照直观的得出了不同的边界吸收条件的吸收效果，对结果进行了对比，分析总结了各种方法的优缺点。

标签：数值模拟；有限差分；边界条件随着近年来国家宏观经济调控，经济增长的速度逐步减缓，能源行业受此影响最为严重，许多煤矿是在亏损的情况下生产，直接导致了地质行业投入的减少。

物探行业压力也越来越大，物探行业应该抓紧发展先进技术，提高能源勘探的效率。

在物探行业中，地震勘探作为一个重要的手段，发挥着巨大的作用。

数据处理作为地震勘探的一大重要环节，所采用的各种方法和技术手段也一直在更新和进步。

在地震勘探处理方法研究中，地震数值模拟技术可以在室内完成地震数据模型的建立，并对其地震数据进行各种方法的处理，查看处理方法的效果和数据的好坏，另一方面，地震数值模拟进行正演获得的数据也可以作为反演的基础进行比对。

在地震数据处理的过程中，如何模拟地震波的传播便是需要解决的问题。

在二十世纪70年代开始采用显示差分格式来模拟地震波的传播。

由于有限差分法适用条件广，计算速度比较快，占用计算机内存少，编程比较容易实现，模拟精度相对较高而得到广泛应用。

但是有限差分法模拟地震波场时，由于计算机运算核心的限制，有限差分方法只能得到有限的数据点，地震波动方程只能是在有限差分方程中求得近似解，这时就考虑到人工边界问题，如果不对边界进行处理，波在通过边界时会产生反射，因此我们希望对添加的边界进行处理来消除这些反射。

在20世纪70年代，地球物理学界陆续采用了不同的边界条件来实现削弱地震波在通过边界时的反射，比如reynold边界、clayton边界、cerjan边界，以及后来提出的PML层边界条件，每种边界条件都在不同程度上实现了地震波通过边界时的衰减。

为了验证以上边界条件在数值模型的效果，在文章中，我们设计了一些简单的数值模型，给出了不同的边界条件，通过波形在通过不同边界条件时反射进行比较，观察每种方法衰减反射的效果。

（7）
⎧P(0, j, k +1) = (2 − 2A − A2 )P(0, j, k) + 2A(1+ A)P(1, j, k)
⎪ ⎪
− A2P(2, j, k) + (2A −1)P(0, j, k −1) − 2AP(1, j, k −1)
⎪⎪P(M , j, k +1) = (2 − 2A − A2 )P(M , j, k) + 2 A(1+ A)P(M −1, j, k)
Chen Jingguo
China University of Geosciences (Beijing) (100083) E-mail: chenjg_cugb@ Abstract
The Finite Difference Method (FDM) is one of the most important methods of seismic wave field numerical modeling. But when we model seismic wave field with FDM, absorption boundary problem should be considered because the machine can not model the geological body of infinite boundary. This paper presents 2-D acoustic wave equation sample, through contrasting effectiveness of non-absorbing with the 1st order and 2nd order absorbing boundary conditions, illuminate the artificial boundary reflection (pseudo-reflection) problem and show the importance of the absorbing boundary conditions. Key words: finite difference method, seismic wave field, numerical modeling, absorbing boundary conditions, pseudo-reflection

第26卷第3期CT理论与应用研究Vol.26, No.3李斌, 温明明, 牟泽霖. 用于声波正演模拟的时空域高精度交错网格有限差分方法[J]. CT理论与应用研究, 2017, 26(3): 259-266. doi:10.15953/j.1004-4140.2017.26.03.01.Li B, Wen MM, Mu ZL. Staggered-grid finite-difference method with high-order accuracy in time-space domains for acoustic forward modeling[J]. CT Theory and Applications, 2017, 26(3): 259-266. (in Chinese). doi:10.15953/j.1004- 4140.2017.26.03.01.用于声波正演模拟的时空域高精度交错网格有限差分方法李斌1，2 ，温明明1，2，牟泽霖1，21.中国地质调查局广州海洋地质调查局，广州5100752.国土资源部海底矿产资源重点实验室，广州510075摘要：地震正演模拟是逆时偏移和全波形反演中的核心问题之一，因为它们都需要高效、高精度地模拟波场正向和反向传播。

为了提高数值模拟的精度，人们广泛采用高阶有限差分方法，但是大多数方法仅在空间上具有更高的精度，在时间上只有二阶精度。

首先系统介绍时空域高精度交错网格有限差分方法的基本原理，然后利用模型验证方法的有效性，结果表明：时空域高精度交错网格有限差分方法拥有比常规交错网格有限差分方法更低的数值频散。

关键词：声波方程正演模拟；时空域；交错网格；有限差分doi:10.15953/j.1004-4140.2017.26.03.01 中图分类号：O242；P631 文献标志码：A在过去数10年里，学者们提出了很多不同形式的有限差分方法，用于提高地震波场数值模拟的精度和效率[1]。