声波方程正演模拟1

声波方程数值模拟实验报告.基础理论知识需要的已知条件包括：1）震源函数地层速度（波速） 边界条件.2.2.2苇=v 2(諾二2)S(t)一 t :x :zv （x, Z ）是介质在点（x , z ）处的纵波速度，u 为描述速度位或者压力的波场，s （t ）为震 源函数。

为求式（4-1）的数值解，必须将此式 离散化，即用有限差分来逼近导数，用差商代替 微商。

为此，先把空间模型网格化（如图4-1所示）。

设x 、z 方向的网格间隔长度为h ，厶t 为时间采样步长，则有:X 二i^h（i 为正整数） z = j.）h（j 为正整数）^n ：t（n 为正整数）u ：j 表示在（i,j ）点，k 时刻的波场值。

k1. 2)3)>2u 2f cu〒=V p ^~2 t :x22w 2 w 厂二 V （—T :t ；x 声波方程的有限差分法数值模拟 对于二维速度-深度模型，地下介质中地震波的传播规律可以近似地用声波方程描述:2. 弹性波方程:二b s (t) 一 z22_w )；z 2)(4-1)将u i,j在（i,j）点k时刻用Taylor展式展开：k 1 kjUu i,j 7,j ■—ct将U i k j 」在(i,j)点k 时刻用Taylor 展式展开:k k4 k k5 k[U i2jui 2,j] 3[ui 4,j ui ・1,j] —?U i,j }S(t)*、(i -i °)**「(j - j °)(4-7)式中v(i, j)为介质速度的空间离散值，：h 是空间离散步长，=t 为时间离散步长，s(k)为震源函数，关于 s(k) 一般使用一个理论的雷克型子波代替，即:上式中，t 为时间，f 为中心频率，一般取为20-40HZ ， 为控制频带宽度的参数,(4-2)k 1k ；'UUi,jUi,2*「7 2 ；:t 2(4-3)将上两式相加，略去高阶小量, 整理得(i,j)点k 时刻的二阶时间微商为:2k 1kk J；：u u i,j -2u i,j u i,j.:t 242(4-4)对于空间微分，采用四阶精度差分格式,(以X 方向为例)即将U i*；j 、*Tj 分别在(i,j)点k 时刻展开到四阶小量，消除四阶小量并解出二阶微分得:-2~ u 11 k k 4 k k 5 k{—T7[u i 二 j +u id2,j ]+：[u i4j +U i*,j ] —=u i,j } 12 3 2:x L X 2(4-5)同理可得:2；=u 1.1 kk4 kk5 k一 2 人 2{一 石[Ui,j ，+Ui,j~2]+：[Ui,j 」+Ui,j^]—；U i,j}:z-z12 32(4-6)这就实现了用网个点波场值的差商代替了偏微分方程的微商，将上三个式子代入 (4-1)式中得:k 1 Ui,j kk 4= 2u i,j —Ui,jV :-1 1 k k 4 k k—{p [u=j U i/ yij —j：h 25 k H-U i,j }h 2 {12s (t )二 e(-2 f / )2t2cos2 二 ft(4-8)般取3-5。

题目：使用Ricker 子波，刚性边界条件，并且初值为零，在均匀各向同性介质条件下，利用交错网格法求解一阶二维声波方程数值解。

解：一阶二维声波方程：22222221zPx P t P c ∂∂+∂∂=∂∂ (1)将其分解为：21P c t Px P z x z x z V V x z V tV t ∂∂∂⎧=+⎪∂∂∂⎪∂∂⎪=⎨∂∂⎪∂∂⎪=⎪∂∂⎩(2)对分解后的声波方程进行离散，可得到：112211,-1,,,122[]N n n n n m i m j i m j xi j xi j m t VVc P P h +-+---=∆=+-∑ 112211,1,,,122[]Nn n n n m i j m i j m zi j zi j m t VV c P P h +-++---=∆=+-∑ 1111212222,,m 1,,,,11[]Nn n n n n n i ji jmxi j xi m j zi j m zi j m m tc PP cVVVVh+++++++-+--=∆=+-+-∑h z x =∆=∆针对公式(1)，使用二阶中心差商公式：2P(,,1)2(,,)(,,1)i j n P i j n P i j n t +-+-∆222(1,,)2(,,)(1,,)(,1,)2(,,)(,1,)P i j n P i j n P i j n xc P i j n P i j n P i j n z +-+-⎧⎫+⎪⎪⎪⎪∆=⎨⎬+-+-⎪⎪⎪⎪⎩∆⎭(3)变形：P(,,1)=2(,,)(,,1)i j n P i j n P i j n +--2222(1,,)2(,,)(1,,)t (,1,)2(,,)(,1,)P i j n P i j n P i j n xc P i j n P i j n P i j n z +-+-⎧⎫+⎪⎪⎪⎪∆+∆⎨⎬+-+-⎪⎪⎪⎪⎩∆⎭(4)对离散格式作时间和空间三重Fourier 变换：0P(,,)(,,)x z i j n P k k w ↔ ，0P(,,1)(,,)*exp()x z i j n P k k w iw t +↔∆0P(1,,)(,,)*exp(k )x z x i j n P k k w i x +↔-∆，0z P(,1,)(,,)*exp(k )x z i j n P k k w i z +↔-∆对公式(4)进行Fourier 变换：2222exp()2exp()h exp()2()exp()2exp()h x x z z ik x ik x iw t iw t t c ik z ik z -∆-+∆⎡⎤+⎢⎥∆=--∆+∆⎢⎥-∆-+∆⎢⎥⎢⎥⎣⎦2222exp()2exp()h exp()2()=exp()2exp()h x x z z ik x ik x iw t iw t t c ik z ik z -∆-+∆⎡⎤+⎢⎥∆-+-∆∆⎢⎥-∆-+∆⎢⎥⎢⎥⎣⎦222222sin sin 22sin (2x z k x k zw tt c h∆∆+∆=∆） (5) 公式(5)右端必须满足下列条件：22222sin sin 220(x z k x k zt c h∆∆+≤∆≤）1 取x k 和z k 最大值，即=x x k π∆，z =k z π∆，则有：22220t c h≤∆≤1因此tc ∆≤即为所求得的稳定性条件。

波动方程正演模拟边界条件的比较分析付小波;韩超;原健龙;余嘉顺【摘要】通过数值模拟研究了透明边界、Clayton-Engquist边界和完全匹配层边界的吸收效果,得出如下结论:在反射角和频率相同的情况下,完全匹配层边界条件效果最好,Clayton-Engquist边界效果次之,而透明边界条件的效果最差.以边界条件对100 Hz模型边界垂直反射的吸收效果来衡量,完全匹配层边界条件与Clayton-Engquist边界条件的效果分别是透明边界条件的16.5倍和3.5倍.在＜40 Hz的低频范围内,或者在反射角＞65°的情况下,Clayton-Engquist边界相对透明边界的吸收效果相对优势显著变弱.而完全匹配层边界的吸收效果则在150 Hz频率范围内和75°反射角范围内始终保持稳定的相对优势.【期刊名称】《成都理工大学学报（自然科学版）》【年(卷),期】2015(042)004【总页数】8页(P492-499)【关键词】波动方程;正演模拟;有限差分;边界条件【作者】付小波;韩超;原健龙;余嘉顺【作者单位】成都理工大学地球物理学院,成都610059;成都理工大学地球物理学院,成都610059;成都理工大学地球物理学院,成都610059;成都理工大学地球物理学院,成都610059;新西兰皇家地质与核科学研究所,惠灵顿【正文语种】中文【中图分类】P631.4边界条件是地震波数值模拟方法技术中的一项重要内容。

许多专家学者从不同角度提出多种构造边界条件的方法。

1977年，Clayton与Engquist［1］根据旁轴近似理论（Claerbout［2］；Claerbout与Johnson［3］），提出利用一系列不同近似精度的单程波动方程来吸收模型边界的反射能量，称作Clayton-Engquist （下文采用简略记号CE来表达）边界条件。

1978年，Reynolds通过对波动方程的分解得到了透明边界条件［4］（下文采用简略记号TBC来表达）。

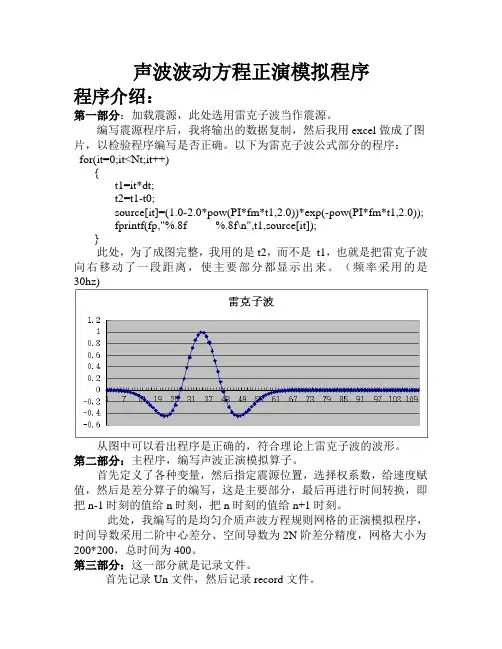
声波波动方程正演模拟程序程序介绍：第一部分：加载震源，此处选用雷克子波当作震源。

编写震源程序后，我将输出的数据复制，然后我用excel做成了图片，以检验程序编写是否正确。

以下为雷克子波公式部分的程序：for(it=0;it<Nt;it++){t1=it*dt;t2=t1-t0;source[it]=(1.0-2.0*pow(PI*fm*t1,2.0))*exp(-pow(PI*fm*t1,2.0));fprintf(fp,"%.8f %.8f\n",t1,source[it]);}此处，为了成图完整，我用的是t2，而不是t1，也就是把雷克子波向右移动了一段距离，使主要部分都显示出来。

（频率采用的是30hz)从图中可以看出程序是正确的，符合理论上雷克子波的波形。

第二部分：主程序，编写声波正演模拟算子。

首先定义了各种变量，然后指定震源位置，选择权系数，给速度赋值，然后是差分算子的编写，这是主要部分，最后再进行时间转换，即把n-1时刻的值给n时刻，把n时刻的值给n+1时刻。

此处，我编写的是均匀介质声波方程规则网格的正演模拟程序，时间导数采用二阶中心差分、空间导数为2N阶差分精度，网格大小为200*200，总时间为400。

第三部分：这一部分就是记录文件。

首先记录Un文件，然后记录record文件。

模型构建与试算：1、我首先建立了一个均匀介质模型，首先利用不同时间，进行了数值模拟，得到波场快照如图所示：100ms 200ms 300ms此处，纵波速度为v=3000m/s。

模型大小为200×200，空间采样间隔为dx=dz=10m。

采用30Hz的雷克子波作为震源子波，时间采样间隔为1ms，图中可以看出，波场快照中的同相轴是圆形的，说明在均匀各向同性介质中，点源激发的波前面是一个圆，这与理论也是吻合的。

并且随着时间的增大，波前面的面积逐渐增大，说明地震波从震源中心向外传播。

声音的波动方程声音是一种能够通过空气、水等介质传导的物理现象，而声音的波动方程就是描述声波在介质中传播时的数学公式。

以下将从几个步骤来阐述声音的波动方程。

第一步：介质的振动声波是由介质分子的振动引起的，当声波在介质中传播时，它们会引起介质的周期性振动。

因此，声波可以被视为机械波，与大多数其他类型的波一样，它是由波的振幅、频率和波长三个要素确定的。

第二步：波的传播速度声波的传播速度取决于介质的密度、弹性模量和介质的压缩性等因素。

根据拉普拉斯原理，和波源和接收器之间的距离有关，声波的传播速度可以写成一个公式：v=fλ其中v是声波的传播速度，f是声波的频率，λ是声波的波长。

第三步：声波的压强变化声波的传播是通过介质压强变化的方式来实现的。

当声波通过介质时，它们会引起介质的压缩和膨胀。

这导致压强在空气中产生变化，使空气分子在颤动。

通过这种方式，声波在空气中传播。

第四步：声波的波动方程声波的波动方程可以用下列偏微分方程表示：∇²p(x,y,z)-1/v²*(∂²p(x,y,z)/∂t²)=0其中∇²是拉普拉斯算子，p（x、y、z，t）是压强（即声波的幅度）的空间和时间变化，v是声波的传播速度。

在坐标系中，x、y、z表示空间位置变量，t表示时间变量。

因此，这个方程可以解释为“空间中压强的二阶时间倒数等于时间中压强的拉普拉斯算子除以速度的平方”。

结论声音的波动方程是根据物理原理得出的，在声波传播的所有过程中都起到了关键作用。

通常情况下，声波在介质中的传播速度、波长、频率和波幅等特性由声音的波动方程计算得出。

因此，声音的波动方程是研究声波性质和声学的重要基础。

声波及粘声波波动方程正反演方法研究下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢！本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注！Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!声波及粘声波波动方程正反演方法研究1. 引言声波及粘声波波动方程的研究在地球物理探测和工程领域具有重要意义。

本科毕业设计（论文）题目：粘声波正演模拟方法研究学生姓名：xxx学号：xxx专业班级：xxx指导教师：xxx2015年 6月20日粘声波正演模拟方法研究摘要地球上介质的黏滞性会引起大地的吸收效应,它会影响波场所有的频率成分,尤其对于高频的影响最大,导致地震分辨率降低。

黏滞吸收作用会影响地震波波形、频带、振幅等因素。

一个高效的粘声波正演模拟方法，可以考虑到由于实际介质造成的地震波的吸收衰减作用。

可以更加准确模拟地震波在非完全弹性实际地层中的传播，在这里，本文通过编程建立不同的粘声波方程数值模拟模型跟正常的声波方程数值模拟模型进行对比分析，从而了解粘声波正演模拟方法的优越性。

关键词：粘声波；正演模拟；有限差分；Study on the forward modeling of viscoelastic acousticwavesAbstractThe absorption effect is mainly caused by the viscosity of the earth media itself.The viscous stagnation can affect all the frequency components of the wave field.And the effect of the high frequency components is bigger,which leads to the decrease of seismic resolution.The absorption of the absorption has a great influence on the wave, frequency and amplitude of the seismic wave.. A highly effective viscoelastic forward modeling method can take into account the absorption and attenuation of seismic waves by real media.. Accurate simulation of the propagation of seismic waves in the actual strata of the imperfect elasticity. Here. In this paper, the program, establish different visco acoustic wave equation numerical simulation model with normal acoustic wave equation numerical simulation model for comparative analysis, to understand the visco acoustic forward modeling method of superiority.Keywords：Viscoelastic acoustic wave；Viscoelastic acoustic wave；Finite difference;目录第1章引言 (1)1.1 研究意义 (1)1.2 正演模拟方法 (1)1.3 国内外研究现状 (3)1.4 本论文研究内容 (3)第2章粘性介质基本理论 (5)2.1 粘性介质的基本特点 (5)2.2 粘性介质模型的构建 (6)2.2.1 开尔芬固体模型 (6)2.2.2 标准线性体 (7)2.3 品质因子 (7)2.3.1 定义 (8)2.3.2 与吸收系数 的关系 (8)2.3.3 与介质速度v的关系 (8)2.3.4 与震源频率的关系 (8)第3章二维各向同性介质粘声波方程数值模拟 (10)3.1 粘声波方程及其交错网格高阶差分格式 (10)3.1.1 粘声波方程的推导 (10)3.1.2 速度-应力方程的推导 (11)3.1.3 交错网格有限差分 (12)3.2 模拟震源 (16)3.2.1 震源的选择 (16)3.2.2 震源的类型 (17)3.3 边界条件 (18)3.3.1 衰减边界条件 (19)3.3.2 PML边界条件 (19)3.4 稳定性 (20)3.5 数值频散问题 (22)3.6 模型试算 (23)3.6.1地震波的传播规律研究 (23)3.6.2 粘声波的衰减规律研究 (27)第4章结论 (28)致谢 (30)参考文献 (31)第1章引言1.1 研究意义我国的石油天然气等资源类工业发展的非常快，随着油气资源的不断发现并且开采，现阶段所存在的油气资源越来越少，因此油气勘探工作变的越来越困难。

波动方程正演模型及应用吴清岭　张　平　施泽龙3(大庆石油管理局勘探开发研究院)摘　要　地震资料解释经常用到正演模型。

常规的褶积模型不能模拟地震波的动力学特征。

本文采用声波方程,通过四阶有限差分近似,实现了复杂地质构造零炮检距的数值模拟。

文中同时展示了实际应用效果。

　主题词　正演模型 有限差分 零炮检距剖面作者简介　吴清岭,男,1962年生,1983年毕业于华东石油学院勘探系,硕士,高级工程师,现从事地震方法研究工作。

地址:(163712)黑龙江省大庆市让胡路区勘探开发研究院。

3　参加本工作的还有杨有林同志。

在地震资料解释中,人们力图得到能够保持地震波的运动学与动力学特征的波动方程正演模型,以达到精确模拟地震波传播特性的目的。

在求解波动方程的2种数值解法(有限差分法和有限元法)中,有限差分法是一种快速有效的方法,并且地质模型的复杂程度不影响运算速度。

本文介绍了对声波方程采用四阶有限差分近似制作零炮检距剖面的基本过程及应用效果。

一、基本原理1,计算公式在二维空间域内,二维声波方程为1C 292u 9t 2=92u 9x 2+92u9z 2式中　C ———声学介质下地震波的纵波速度;u ———声压。

设Δh 为空间采样步长;Δt 为时间采样步长;m 、n 、l 分别为正整数;则有x =m ・Δh z =n ・Δh t =l ・Δt 对时间域采用二阶有限差分;对空间域采用四阶有限差分(推导过程略),其数值计算公式为u (m ,n ,l +1)=(A 2/12){16[u (m +1,n ,l )+u (m -1,n ,l )+u (m ,n +1,l )+u (m ,n -1,l )]-[u (m +2,n ,l )+u (m -2,n ,l )+u (m ,n +2,l )+u (m ,n -2,l )]}+(2-5A 2)[u (m ,n ,l )-u (m ,n ,l -1)]其中 A 2=C 2(m ,n )Δt 2/Δh 2式中　C (m ,n )———介质速度的空间离散值;Δt ———时间离散步长;Δh ———空间离散步长。

声学波的数学模型及其应用随着声学科学的深入研究，声波在各个领域得到了广泛应用。

为了更好地利用声波的特性进行科学研究和实践操作，人们需要对声波进行数学建模，以深入理解声波的规律和特性。

本文将探讨声学波的数学模型及其应用，希望能够帮助大家进一步了解声学波在实际应用中的重要性。

一、声学波的数学模型声波是一种机械波，是由介质中质点受到扰动而引起的机械振动。

声波产生的传播过程可以用波动方程来描述，其基本形式如下：∂²u/∂t²=c²∇²u其中，u 表示声波振幅，t 表示时间，c 表示声速，∇²表示Laplacian 算子。

这个方程描述了声波传播的基本规律：声波的振动在介质中以波速 c 传播，并且具有波动方程的特性。

在实际应用中，人们可以通过这个方程来预测声波的传播规律和特性，以便更好地应用声波进行实验和研究。

除了波动方程，人们还可以用其他数学模型来描述声波的特性。

例如，人们可以用声学爆轰模型来模拟空气中的声音传播。

该模型基于 Navier-Stokes 方程，其中包含了密度、声速、温度和速度等多个物理因素，可以更准确地描述声波的传播过程。

二、声学波在各个领域的应用1. 医疗领域在医疗领域，人们广泛使用声波进行诊断和治疗。

例如，超声波可以通过机身的扫描来捕捉体内器官的图像，以检查人体的内部状况。

同时，超声波也可以治疗人体的一些疾病，如肿瘤等。

此外，医疗领域还使用其他声学波进行实验和研究，以便更好地了解人体的生理特性。

2. 工业领域在工业领域，声波也有许多应用。

例如，声波可以帮助人们检测材料的缺陷和强度，以便更好地选择和使用材料。

此外，声波还可以用于油井和矿井等地下领域的勘探和研究，以便更好地发掘和利用地下资源。

3. 娱乐领域在娱乐领域，声波也有很多应用。

例如，人们可以通过声波来创造音乐，让人们享受美妙的音乐盛宴。

此外，声波还可以用于游戏和电影中，以增强观众的游戏体验和感官享受。

Open Journal of Natural Science 自然科学, 2020, 8(4), 258-263Published Online July 2020 in Hans. /journal/ojnshttps:///10.12677/ojns.2020.840342D Acoustic Wave Equation ForwardModeling in the Frequency DomainKun Han, Xiangchun Wang*School of Geophysics and Information Technology, China University of Geosciences (Beijing), BeijingReceived: Jun. 23rd, 2020; accepted: Jul. 6th, 2020; published: Jul. 13th, 2020AbstractForward modeling in frequency domain plays an important role in the numerical simulation of seismic waves. Compared with time domain forward modeling, frequency domain forward mod-eling has many advantages, such as suitable multi shot parallel operation, no time dispersion, flexible frequency band selection and small error. The coefficient matrix of different frequencies is relatively independent in the frequency domain forward modeling, which is suitable for the acce-leration of parallel computing and greatly improves the computing efficiency. In this paper, for the optimal 9-point difference scheme of frequency domain acoustic equation, the implicit expression and sparse matrix solution are studied, and the seismic wave field is simulated forward. The ac-curacy and validity of the method are verified by model calculation.KeywordsFrequency Domain, Forward Modeling, Acoustic Equation, Parallel Computing二维频率域声波方程正演模拟韩坤，王祥春*中国地质大学(北京)，地球物理与信息技术学院，北京收稿日期：2020年6月23日；录用日期：2020年7月6日；发布日期：2020年7月13日摘要频率域正演在地震波数值模拟中占有十分重要的地位。

本科生实验报告实验课程油气勘探新方法学院名称地球物理学院专业名称勘查技术与工程（石油物探）学生姓名学生学号指导教师熊高君实验地点5417实验成绩2015年12月成都理工大学《油气勘探新方法》实验报告实验报告一、实验题目叠前地震记录的相移波动方程正演模拟实验二、实验目的掌握各向同性介质任意构造、水平层状速度结构地质模型的叠前地震记录相移波动方程正演模拟基本理论、实现方法与程序编制，由正演记录初步分析地震信号的分辨率。

三、原理公式1、地震波传播的波动方程设（x,z ）为空间坐标，t 为时间，地震波传播速度为v(x,z)，则二维介质中任意位置、任意时刻的地震波场为p(z,x,t)：压缩波——纵波。

则二维各向同性均匀介质中地震波传播遵循的声波方程：ð2p(x,z,t)ðx 2+ð2p(x,z,t)ðz 2=1v 2(x,z)ð2p(x,z,t)ðt 2(1) 2、傅里叶变换的微分性质p(t)与其傅里叶变换的P(ω)的关系：{ P (ω)=∫p (t )e −iωt dt ∞−∞ 正傅里叶变换 p (t )=12π∫P (ω)e iωt dt ∞−∞逆傅里叶变换 (2) 则有时间微分性质：{ (iω)P (ω)=∫dp (t )dt e −iωt dt ∞−∞ 一阶微分 (iω)2P (ω)=∫d 2p (t )dt 2e −iωt dt ∞−∞ 二阶微分 (3) ω为频率，ω=2πT ⁄，T 为周期。

同理有空间微分性质：{ (ik)P (k )=∫dp (x )dx e −ikx dx ∞−∞ 一阶微分 (ik)2P (k )=∫d 2p (x )dx 2e −ikx dx ∞−∞ 二阶微分 (4) k 为波数， k =2πλ⁄， λ为波长。

3、地震波传播的相移外推公式令速度v 不随x 变化，只随z 变化，则利用傅里叶变换微分性质（3）和（4）式，把波动方程(1)式变换到频率‐波数域，得：(ik )2P (k,z i ,ω)+ð2P(k,z,ω)ðz 2=(iω)2v (z )2P (k,z,ω) （5） 或：ð2P(k,z,ω)ðz 2=−(ω2v (z )2−k 2)P (k,z,ω) (6) 令：k z 2=ω2v (z )2−k 2则(6)式的解为：P (k,z,ω)=c 1e −ik z z +c 2e ik z z (7)包括上行波和下行波两项，正演模拟取上行波：P (k,z,ω)=c 1e −ik z z (8)若Z j和Z j+1间隔为∆z，速度v(z)为在此间隔内不随Z变的常数，(8)式实现波场从Z j+1到Z j的延拓，即：P(k,z j,ω)=c1e−ik z∆z（9）在深度Z j+1开始向上延拓到Z j，若延拓深度为零，即：∆Z=Z j+1−Z j，则P(k,z j=z j+1,ω)=c1e−ik z(z j+1−z j)=ce−ik z×0=c (10)对于任意深度Z j+1到Z j的延拓，可得正演模拟中地震波的传播方程（延拓公式）P(k,z j,ω)=P(k,z j+1,ω)c1e−ik z(z j+1−z j) (11) 4、初始条件和边界条件按照爆炸界面理论，反射界面震源在t=0 时刻同时起爆，此时刻的波场就是震源。