3动量角动量机械能

动量守恒角动量守恒机械能守恒三者之
间的关系
动量守恒
动量守恒是指在一个系统中，总动量在没有外力作用下保持不变。

角动量守恒
角动量守恒是指在没有外力矩作用下，物体的角动量保持不变。

机械能守恒
机械能守恒是指在没有非保守力做功的情况下，系统的机械能保持不变。

三者之间的关系
这三个守恒定律都是基于物理系统的某些性质保持不变而提出的，它们有着联系和相互影响的关系。

动量守恒和角动量守恒可以通过物体的质量、速度、角速度、撞击力矩等参数相互转化和计算。

机械能守恒是在没有非保守力做功的情况下成立的，而非保守力做功会改变物体的动能和势能，从而改变机械能。

实例
例如，一个物体在真空中自由下落，由于没有空气阻力和其他阻碍，系统中既没有外力也没有外力矩作用。

在这种情况下，动量守恒、角动量守恒和机械能守恒三者都成立。

物体的动量保持不变，角动量保持不变，机械能（动能+势能）保持不变。

总结
▪动量守恒是指总动量保持不变。

▪角动量守恒是指物体的角动量保持不变。

▪机械能守恒是指系统的机械能保持不变。

以上就是动量守恒、角动量守恒和机械能守恒三者之间的关系的介绍。

力学知识点整理力学是物理学的一个重要分支，它研究的是物体的运动规律和力的作用关系。

在研究物体的运动规律和力的作用关系时，力学涉及到很多重要的知识点。

下面，我们就来整理一下力学的知识点，以便大家更好地掌握这门学科。

一、牛顿力学牛顿力学是力学的基础理论，主要涉及物体的运动规律、力的概念、力的平衡条件、动量定理、角动量定理、机械能守恒定律等内容。

以下是具体的知识点：1. 物体的运动规律：物体的速度在没有外力作用时不变，物体的位置、速度、加速度之间有着确定的关系，即牛顿第二定律F=ma。

2. 力的概念：力是物体作用于其他物体的作用，力的大小和方向分别用标量和矢量表示，力的叠加原理和分解原理。

3. 力的平衡条件：在力的作用下，物体的平衡状态有三种：静止、匀速直线运动、匀速圆周运动。

物体在这三种状态下都要满足力的平衡条件，即受到的合力为零。

4. 动量定理：物体的动量是质量和速度的乘积，动量定理是指物体所受合外力的冲量等于物体动量的增量，即FΔt=Δ(mv)。

5. 角动量定理：物体的角动量是质量、速度和距离的乘积，角动量定理是指物体所受合外转矩的冲量等于物体角动量的增量，即NΔt=Δ(L)。

6. 机械能守恒定律：机械能守恒是指在没有非弹性碰撞的情况下，系统的机械能等于系统的初能与末能之和，即E1=E2。

二、刚体力学刚体力学研究的是刚体的运动规律和力的作用关系，其中包括刚体的平衡条件、刚体的转动、刚体的动量、角动量和机械能等内容。

以下是具体的知识点：1. 刚体的平衡条件：刚体的平衡有两种：平衡和不稳定平衡。

平衡状态下，刚体所受合外力和合外转矩均为零，且由等大反向的内力平衡。

2. 刚体的转动：刚体的转动可以绕固定轴转动和自由转动两种。

固定轴转动下，角度是描绘物体运动状态的重要指标，可用刚体的角速度、角加速度等进行描述。

自由转动下，刚体不围绕任何旋转轴旋转。

3. 刚体的动量：刚体的动量是刚体质量与速度之积，刚体在外力作用下，动量可以变化，变化量与外力冲量相等。

描述动量守恒、机械能守恒和角动量守恒定律。

动量守恒定律是研究物体运动规律的重要基础，它可以完全描述质量和平衡性，解释并预测系统总动量的变化。

这个定律称为动量守恒，也叫受力定理，是物理学中最基本的定律之一，是物理学的核心。

动量守恒定律指的是在不受外力作用的情况下，物体的总动量保持不变，无外
力作用的条件下，物体运动的变化应满足总动量不变，用数学表示为: Momentum= Mass X Velocity
也就是说，如果物体整体的体积和质量是固定的，它的动量就将保持不变。

机械能守恒定律指的是物体在施加外力的情况下，机械能是保持定值不变，也
就是说，机械能会在系统内转化，但总数量不会改变。

机械能守恒定律是从动量定律和能量守恒定律中推导出来的，用公式表示为：
∆K = F·s,其中∆K为机械能变化量，F为作用在物体上的外力，s为外力作用
点在物体位移向量所取得的积分值。

角动量守恒定律指的是在外力作用的情况下，物体的角动量也是保持定值不变的，角动量守恒定律是一个要求物体在外力作用下保持恒定角速度的定律，它体现了物体围绕其轴心进行自旋旋转时，它能保持恒定角速度的能力，用公式表示为：
∆L = τ，其中∆L为角动量变化量，τ为作用于物体的外力矩。

总之，动量守恒定律、机械能守恒定律、角动量守恒定律都是研究物体运动规
律的重要定律，它们根据实际情况有所不同，但它们都是物理学中的基本定律。

力学中的机械能与动量力学是物理学中的一个重要分支，研究物体运动的力学定律。

在力学的研究过程中，机械能和动量是两个核心概念。

机械能是物体在运动中具有的能量，而动量则是运动物体的特性之一。

本文将详细探讨力学中的机械能与动量的相关理论和应用。

一、机械能的概念与计算机械能是由物体的动能和势能组成的。

动能是物体由于运动而具有的能量，计算公式为：动能 = 1/2mv²，其中m为物体的质量，v为物体的速度。

势能是物体由于位置而具有的能量，常见的势能有重力势能和弹性势能。

重力势能是物体在重力作用下具有的势能，计算公式为：重力势能= mgh，其中m为物体的质量，g为重力加速度，h为物体相对于参考点的高度。

弹性势能是物体由于形变所具有的势能，计算公式为：弹性势能 = 1/2kx²，其中k为弹性系数，x为物体的形变量。

机械能可以通过动能和势能的叠加来计算，公式为：机械能 = 动能+ 势能。

在一个封闭系统中，机械能的总量是守恒的，即机械能的增加或减少仅由物体内部的能量转化决定。

二、动量的概念与计算动量是物体运动的一个重要特性，用来描述物体的运动状态。

动量的计算公式为：动量 = mv，其中m为物体的质量，v为物体的速度。

动量是一个矢量量，具有大小和方向。

根据牛顿第二定律，力的大小等于质量乘以加速度，即：F = ma。

应用牛顿第二定律可以推导得到，物体动量的变化量等于物体所受力的大小乘以作用时间，即：Δp = FΔt，其中Δp为物体动量的变化量，F 为物体所受的合力，Δt为作用时间。

在一个封闭系统中，动量的总量也是守恒的，即系统内物体的动量之和保持不变。

这就是著名的动量守恒定律，它是力学中一个重要的基本定律。

三、机械能与动量的应用机械能与动量的理论不仅用于解释物体运动的规律，还有广泛的应用。

以下是两个常见的应用场景：1. 碰撞问题：在物体碰撞过程中，机械能和动量的守恒原理可以帮助我们计算和分析碰撞结果。

动力学三大守恒定律【知识专栏】动力学三大守恒定律1. 引言及概述动力学三大守恒定律是物理学中非常重要的概念，它们为我们理解和描述物体运动提供了基础规律。

这三大守恒定律分别是动量守恒定律、角动量守恒定律和能量守恒定律。

本文将以从简到繁、由浅入深的方式来逐步探讨这三大守恒定律的背后原理和应用，以帮助读者更全面地理解这一主题。

2. 动量守恒定律2.1 动量的基本概念为了更好地理解动量守恒定律，首先需要了解动量的基本概念。

动量是物体运动的数量度，表示物体在运动过程中所具有的惯性。

动量的大小与物体的质量和速度相关，可以用数学公式 p = m * v 表示，其中 p 为动量，m 为物体的质量，v 为物体的速度。

2.2 动量守恒定律的表述根据动量守恒定律，一个封闭系统中物体的总动量在没有外力作用的情况下保持不变。

也就是说，如果一个物体的动量发生改变，那么系统中其他物体的动量总和将相应地发生改变，以保持系统的总动量守恒。

2.3 动量守恒定律的应用动量守恒定律在多个领域中都有应用，例如力学、流体力学和电磁学等。

在碰撞问题中，我们可以利用动量守恒定律来分析碰撞前后物体的速度和质量变化。

在交通事故中，通过应用动量守恒定律，我们可以了解事故发生时车辆的速度和冲击力对乘客的影响，并提出相应的安全建议。

3. 角动量守恒定律3.1 角动量的基本概念角动量是物体绕某一轴旋转时所具有的运动状态，它是描述物体旋转惯性的量度。

角动量的大小与物体的惯性和旋转速度相关，可以用数学公式L = I * ω 表示，其中 L 为角动量，I 为物体的转动惯量，ω 为物体的角速度。

3.2 角动量守恒定律的表述根据角动量守恒定律，一个封闭系统中物体的总角动量在没有外力矩作用的情况下保持不变。

即使系统中发生了旋转速度的改变，但系统的总角动量仍然保持恒定。

3.3 角动量守恒定律的应用角动量守恒定律在天体物理学、自然界中的旋转现象等领域中具有广泛的应用。

它被用来解释行星和卫星的自转、陀螺的稳定性以及漩涡旋转等自然现象。

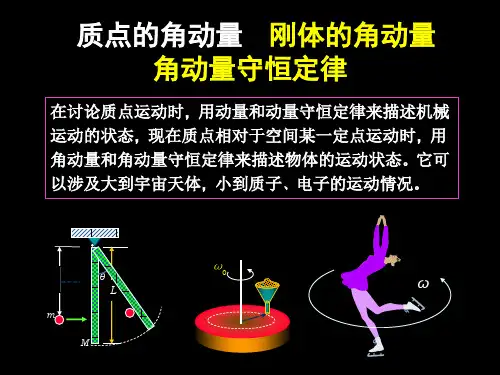
角动量守恒,动量守恒,机械能守恒,冲量守恒条件
动量守恒的条件：外力可以存在，但合外力为零；系统内力可以存在，但是他们合内力零。

机械能守恒条件：重力、弹力等势能性质的力以外的合力为零。

但是重力和弹力势能可以与动能相互转换。

角动量守恒条件：有名动量矩守恒，合外力矩为零，合外力不一定为零。

描述物体运动状况的有2条路线，牛顿发展的是动量变化等于合外力与时间乘积。

莱布尼兹发展的动能的变化是合外力与位移乘积。

2条发展路线争论了好多年，最后才知道2条路线都可以描述物体运动状态。

但是，后来发现动量不能描述旋转物体的状态，一个静止的圆盘和一个旋转圆盘，他们动量都为0，但是一个物体静止一个物体旋转无法区分，所以用角动量来描述物体的状态。

产生角动量守恒定律。

但是“系统所受合冲量为零”就是指整个过程总冲量和为零，不一定是每个微小的时间里都冲量为0，所以一般不说冲量守恒哦~。

第 8 次课 日期 周次 星期 学时2授课内容：§3.1动能定理 机械能守恒定律 1．功； 2．势能；3、刚体转动时合外力矩的功；4、动能定理目的与要求:1．掌握功的定义及变力做功的计算方法，理解力矩的功； 2．掌握保守力和势能的概念，能计算几种常见保守力相关的势能； 3．掌握质点平动和刚体转动时的动能定理； 4. 掌握质点系的动能定理； 重点与难点：1．势能的理解和计算。

2．刚体的转动动能； 3．动能定理的理解和应用。

教学思路及实施方案：通过“力做功”这个具体问题的分析推导，引导学生掌握从简单到复杂、从特殊到一般、由抽象到实际的思维方式。

同时要求学生逐渐能够把数学工具使用到物理中来。

要求学生能够总结出一些常见的势能和动能的处理方式。

§ 3.1 动能定理、机械能守恒定律 一、力对空间的累积效应——功（强调：由浅入深、由抽象到实际的物理思想；与中学相比多了变量的概念和矢量的概念）1、恒力对匀速直线运动物体的功：cos A Fs F s F s τθ===⋅v v2、变力对直线运动物体的功：（涉及一套分析方法）cos .dA F ds θ=（在图中分析）元功：功：222111cos s s s s s s A F ds F ds F dsτθ=⋅=⋅=⋅⎰⎰⎰v v ，举例：漏水桶提水，F 是随着位置变化的。

示功图：F s -图，物理含义：曲线下的面积表示功。

3、变力对曲线运动物体所做的功：元功：cos i i i i A F s θ∆=⋅∆，总功：1cos i i i ii A A F s θ==∆=⋅∆∑∑一般情况：cos b bba a a A F ds F ds F dsτθ=⋅=⋅=⋅⎰⎰⎰v v（引导学生区分：中学计算公式比较，力和路径均是变化的，而且加强矢量的概念）4、功率：cos cos dA F dsN Fv F v F v dt dt τθθ⋅====⋅=v v举例：汽车上坡需牵引力增大，加油门→功率p ，换档→牵引力F 、对应改变速度v5、保守力的功 （1）、重力的功全程的功：i i A A mg h mgh=∆=∆=∑∑重力做功的特点：重力做功与运动路径无关，只与始末位置有关。

动量守恒、角动量守恒和机械能守恒三者之间的关系概述在物理学中，动量、角动量和机械能是三个重要的物理量，它们分别描述了物体的运动状态、旋转状态和能量状态。

这三个物理量都有一个共同的特点，就是在一定的条件下，它们都是守恒的，即不随时间变化。

这些条件通常是指系统不受外力或外力矩的作用，或者外力或外力矩对系统做的功或做的角功为零。

这些条件也可以称为系统是孤立的或封闭的。

动量守恒、角动量守恒和机械能守恒是物理学中最基本和最普遍的定律之一，它们反映了自然界中存在的一种对称性和不变性。

这些定律可以用来分析和解决许多物理问题，例如碰撞、转动、振动、轨道运动等。

在这篇文章中，我们将介绍这三个定律的含义、推导和应用，并探讨它们之间的关系。

动量守恒定义动量是一个矢量物理量，表示物体运动状态的大小和方向。

动量的定义公式为：→p=m→v其中，→p是动量，m是质量，→v是速度。

根据定义，可以看出动量与质量和速度都有关，如果物体的质量或速度发生变化，那么动量也会发生变化。

动量守恒定律是指，在一个孤立系统中，系统内各个物体之间相互作用时，系统总动量不随时间变化，即：→P=n∑i=1→p i=常数其中，→P是系统总动量，→p i是第i个物体的动量，n是系统内物体的个数。

根据定义，可以看出动量守恒定律要求系统内没有外力作用，或者外力对系统做的功为零。

推导动量守恒定律可以从牛顿第二定律推导出来。

牛顿第二定律是指，在一个惯性参考系中，物体所受合外力与其质量乘以加速度成正比，即：→F=m→a其中，→F是合外力，→a是加速度。

根据定义，可以看出合外力与加速度都是矢量物理量，方向相同。

对于一个孤立系统中的任意两个物体A和B，根据牛顿第三定律（作用力与反作用力大小相等、方向相反），我们有：→FAB=−→F BA其中，→F AB是A对B的作用力，→F BA是B对A的反作用力。

由于系统内没有其他外力作用，所以这两个力就是系统内各个物体所受的合外力。