第5讲-垂直平分线与角平分线(上))

七下第5讲三⾓形内外⾓平分线夹⾓模型归纳与内外⾓和计算⽅法总结写在前⾯在前四讲中，我们对本章的重点内容作了归纳，剩下的知识点仅剩⼀个重要模型和内外⾓的相关题型变式，就以本讲作为本章的收尾，更多的难题，留⾄期中复习吧．⼀、三⾓形内外⾓平分线夹⾓模型模型呈现：如图，已知，在△ABC中，BD平分∠ABC，CD平分∠ACB，CH平分∠ACI，BG平分∠EBC，CG平分∠BCF．试探究∠BDC，∠BHC，∠BGC与∠A的关系．分析：这是本章的最后⼀个重要模型，要结合整体思想，外⾓定理综合运⽤．解答：补充结论：其实这个模型中，还能有许多发现，⽐如，∠GBD＝90°，∠DCH＝90°，理由是邻补⾓的⾓平分线互相垂直．∠BGC和∠BHC互余，∠BGC和∠BDC互补，在△DCH中，∠BDC作为外⾓，∠BDC＝90°＋∠BHC．例1：如图，O是三⾓形三条⾓平分线的交点，∠1＝15°，则∠2＝_____°．分析：本题的关键是，发现∠2的作⽤，∠2可以作为△AOB的外⾓，即∠OAB和∠OBA的和，⼜是∠AOB的邻补⾓，∠AOB是三⾓形两内⾓平分线的夹⾓，因此本题既可以⽤⼀步⼀步完成，也可⽤结论模型⼝算．解答：例2：如图，在△ABC中，∠A＝60°，BD、CD分别平分∠ABC、∠ACB，M、N、Q分别在DB、DC、BC的延长线上，BE、CE分别平分∠MBC、∠BCN，BF、CF分别平分∠EBC、∠ECQ，则∠F＝_______．分析：本题是⼀道将三个模型结合在⼀起的题⽬，我们要关注哪些⾓可以求，∠BDC是两内⾓平分线的夹⾓，则知道∠A即可求，∠E是两外⾓，∠MBC，∠NCB的⾓平分线的夹⾓，则知道∠BDC即可求，∠F是△EBC的内⾓∠EBC和外⾓∠ECQ的⾓平分线夹⾓，则知道∠E即可求．解答：例3：分析：解答：综上所述，结论正确的是①②③⑤共4个．⼆、多边形内外⾓计算例1：⼀个学⽣计算多边形的内⾓和，少算了⼀个内⾓，得到答案是1400°，求少算的内⾓的度数及多边形边数．分析：显然，根据多边形内⾓和公式(n－2)·180°，可知内⾓和⼀定是180度的倍数，我们可以⽤1400除以180，算出其余数，那么⾃然可得，少算的那个内⾓与余数的和⼀定是180度的倍数，⽽根据多边形每个内⾓必然⼩于180°，则这个内⾓度数就是⽤180°减去这个余数即可．解答：1400°÷180°＝7······140°，180°–140°＝40°，设多边形边数为n，(n–2)·180＝1400＋40，n＝10答：少算的内⾓度数为40°，边数为10．例2：⼀个学⽣计算多边形的内⾓和，多算了⼀个外⾓，得到答案是1400°，求多算的外⾓的度数及多边形边数．分析：显然，本题是上⼀题的变式，⽅法还是⽤1400除以180，算出其余数，那么多算的外⾓度数，就是这个余数．解答：1400°÷180°＝7······140°，设多边形边数为n，(n–2)·180＝1400－140，n＝9答：多算的外⾓度数为140°，边数为9．例3：⼀个多边形每个内⾓都等于150°，求这个多边形的边数．分析：本题不难，但我们要学会多种思路解题，可以从多边形内⾓和公式⼊⼿，也可以逆向思维，求出每个外⾓的度数，⽤外⾓和除以每个外⾓的度数．解答：法1：设多边形边数为n，(n–2)·180＝150n，n＝12法2：180°－150°＝30°，360°÷30°＝12答：多边形边数为12．三、作图探究例：在△ABC中，∠ACB＝90°，BD是△ABC的⾓平分线，P是射线AC上任意⼀点(不与A、D、C三点重合)，过点P作PQ⊥AB，垂⾜为Q，交直线BD于E．(1)探索∠PDE与∠PED的关系，画出图形并说明理由．(2)作∠CPQ的⾓平分线交直线AB于点F，则PF与BD有怎样的位置关系？画出图形并说明理由．分析：本题中，点P的位置不确定，在射线AC上，就有多种可能，线段AD上，线段DC上，线段DC延长线上，在延长线上时，⼜要考虑垂⾜Q的位置，可能在线段AB上，也可能在线段AB的延长线上．因此，分四种情况讨论．碍于篇幅，我们将两⼩题的图汇总在⼀起．解答：①点P在线段AD上(1)∵PQ⊥AB，∴∠EQB＝∠C＝90°，∴∠PED＋∠EBQ＝90°，∠CBD＋∠CDB＝90°，∵∠PDE＝∠CDB，∴∠CBD＋∠PDE＝90°，∵BD为∠ABC的平分线，∴∠CBD＝∠EBQ，∴∠PDE＝∠PED；(2)在四边形PQBC中，∠CPQ＋∠CBA＝360°－2×90°＝180°∵PF平分∠CPQ，BD平分∠CBA∴∠1＋∠2＝90°∵∠1＋∠3＝90°∴∠2＝∠3，PF∥BD②点P在线段DC上(1)∵PQ⊥AB，∴∠EQB＝∠C＝90°，∴∠BEQ＋∠EBQ＝90°，∠CBD＋∠PDE＝90°，∵∠PED＝∠BEQ，∴∠PED ＋∠EBQ＝90°，∵BD为∠ABC的平分线，∴∠CBD＝∠EBQ，∴∠PDE＝∠PED；(2)在四边形PQBC中，∠CPQ＋∠CBA＝360°－2×90°＝180°∵PF平分∠CPQ，BD平分∠CBA∴∠1＋∠2＝90°∵∠1＋∠3＝90°∴∠2＝∠3，PF∥BD③点P在线段DC延长线上，点Q在线段AB上(1)∵PQ⊥AB，∴∠EQB＝∠ACB＝90°，∴∠BEQ＋∠EBQ＝90°，∠CBD＋∠PDE＝90°，∵∠PED＝∠BEQ，∴∠PED ＋∠EBQ＝90°，∵BD为∠ABC的平分线，∴∠CBD＝∠EBQ，∴∠PDE＝∠PED；(2)∵∠CPQ＋∠A＝90°∠CBA＋∠A＝90°∴∠CPQ＝∠CBA∵PF平分∠CPQ，BD平分∠CBA∴∠1＝∠2∵∠1＋∠3＝90°∴∠2＋∠3＝90°，PF⊥BD④点P在线段DC延长线上，点Q在线段AB延长线上(1)∵PQ⊥AB，∴∠EQB＝∠ACB＝90°，∴∠PED＋∠EBQ＝90°，∠CBD＋∠PDE＝90°，∵∠ABD＝∠EBQ，∴∠PED ＋∠ABD＝90°，∵BD为∠ABC的平分线，∴∠CBD＝∠ABD，∴∠PDE＝∠PED；(2)∵∠CPQ＋∠A＝90°∠CBA＋∠A＝90°∴∠CPQ＝∠CBA∵PF平分∠CPQ，BD平分∠CBA∴∠1＝∠2∵∠1＋∠3＝90°∴∠2＋∠3＝90°，PF⊥BD上讲思考题答案。

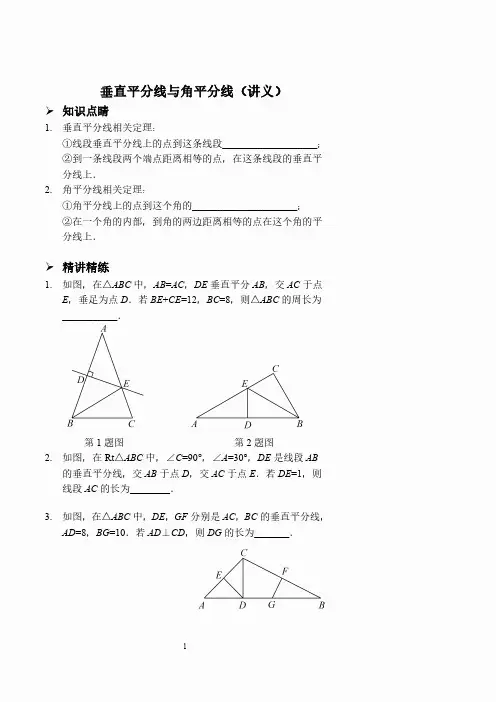
垂直平分线与角平分线（讲义）知识点睛1.垂直平分线相关定理：①线段垂直平分线上的点到这条线段___________________；②到一条线段两个端点距离相等的点，在这条线段的垂直平分线上．2.角平分线相关定理：①角平分线上的点到这个角的_____________________；②在一个角的内部，到角的两边距离相等的点在这个角的平分线上．精讲精练1.如图，在△ABC中，AB=AC，DE垂直平分AB，交AC于点E，垂足为点D．若BE+CE=12，BC=8，则△ABC的周长为___________．第1题图第2题图2.如图，在Rt△ABC中，∠C=90°，∠A=30°，DE是线段AB的垂直平分线，交AB于点D，交AC于点E．若DE=1，则线段AC的长为________．3.如图，在△ABC中，DE，GF分别是AC，BC的垂直平分线，AD=8，BG=10．若AD⊥CD，则DG的长为_______．4.如图，AD与BC相交于点O，OA=OC，∠A=∠C，BE=DE．求证：OE垂直平分BD．5.如图，BD平分∠ABC，DE⊥AB于点E，AB=8，BC=6．若S△ABC=14，则DE=__________．第5题图第6题图6.如图，PC⊥OA于点C，PD⊥OB于点D，且PC=PD，点E在射线OA上，若∠AOB=60°，∠OPE=80°，则∠AEP的度数为_________．7.如图，在△ABC中，∠ABC的平分线与∠ACB的平分线相交于点O，OD⊥AB，OE⊥AC，垂足分别为点D，E．求证：OD=OE．8.已知：如图，△ABC的外角∠CBD和∠BCE的平分线相交于点F，求证：点F在∠DAE的平分线上．9.如图，直线y=x+4与x轴、y轴分别交于点A，B，点C在x轴正半轴上，且OC=OB，点D位于x轴上点C的右侧，连接BC，∠BAO和∠BCD的平分线AP，CP相交于点P，连接BP，则∠PBC的度数为__________．10.如图，在Rt△ABC中，∠C=90°，在AC和AB上分别截取AE，AD，使AE=AD．再分别以点D，E为圆心，大于12 DE的长为半径作弧，两弧在∠BAC内交于点F，作射线AF交边BC于点G．若CG=4，AB=10，则△ABG的面积为________．第10题图第11题图11.如图，在△ABC中，∠B=35°，∠ACB=75°，请依据尺规作图的痕迹，计算∠α=__________．12.过直线上一点，作已知直线的垂线．已知：A为直线MN上一点．求作：直线AB，使AB⊥MN．作法：①以点A为圆心，任意长为半径作弧，交直线MN于C，D两点；②分别以______，______为圆心，_________为半径作弧，两弧交MN上方于一点B；③______________．______________即为所求．13.过直线外一点，作已知直线的垂线．已知：A为直线MN外一点．求作：直线AB，使AB⊥MN．作法：①在MN下方任取一点P；②以_____为圆心，______为半径作弧，交MN于C，D两点；③分别以______，______为圆心，_________为半径作弧，两弧交MN下方于一点B；④______________．______________即为所求．14.如图，已知△ABC，求作：（不写作法，保留作图痕迹）（1）AC边上的高；（2）BC边上的高．15.如图，C，D是∠AOB内部两点，在∠AOB内部求作一点P，使PC=PD，并且使点P到∠AOB两边的距离相等．（不写作法，保留作图痕迹）16.已知：如图，∠ABC，点D在射线BC上．求作：等腰△PBD，使线段BD为等腰△PBD的底边，点P 在∠ABC内部，且点P到∠ABC两边的距离相等．（不写作法，保留作图痕迹）17.如图，A，B是平面上的两定点，在平面上找一点C，使△ABC是以点C为直角顶点的等腰直角三角形，这样的点C有几个？请用尺规作图确定点C的位置，保留作图痕迹．【参考答案】课前预习1.①两个端点的距离相等2.①两边的距离相等精讲精练1.322.33.64.证明略；提示：证△AOB≌△COD（ASA），得到OB=OD，再结合BE=DE，由“到一条线段两个端点距离相等的点，在这条线段的垂直平分线上”得证5.26.110°7.证明略；提示：由“角平分线上的点到这个角的两边的距离相等”可证OD=OF=OE8.证明略；提示：过点F分别作FG⊥AD于G，FH⊥AE于H，FK⊥BC 于K，先由“角平分线上的点到这个角的两边的距离相等”可证FG=FK=FH，再由“在一个角的内部，到角的两边距离相等的点在这个角的平分线上”求证9.45°10.2011.75°12.①点C；点D；大于1CD的长；③作直线AB；直线AB213.②点A；AP长；③点C；点D；大于1CD的长；③作直线2AB；直线AB14.作图略提示：过直线外一点作已知直线的垂线；15.作图略提示：作线段CD的垂直平分线和∠AOB的角平分线；16.作图略提示：作线段BD的垂直平分线和∠ABC的角平分线；17.这样的点C有2个，作图略。

角平分线三个定理-概述说明以及解释1.引言1.1 概述角平分线三个定理是解决与角度相关的几何问题时，非常重要且常用的定理。

它们分别应用于角的平分线问题，帮助我们更深入地理解角的性质与构造。

这三个定理不仅在数学学科中有广泛的应用，而且在实际生活中也具有重要的意义。

在解释这三个定理之前，我们先回顾一下角的基本概念。

在几何学中，角是由两条线段或射线共享一个公共端点而形成的图形。

以公共端点为中心，可以将角分为两个部分，分别称为角的两个腿。

角的大小通常用度或弧度来表示，这取决于所用的单位。

第一个定理是角的平分线定理，它指出：如果一条直线将一个角平分成两个相等的角，那么这条直线称为这个角的平分线。

换句话说，平分线将角分为两个相等的部分。

这个定理有广泛的应用，例如在三角形中，利用角平分线定理可以证明角的大小相等，从而推导出三角形的一些特殊性质。

第二个定理是外角平分线定理，它指出：如果一条直线通过一个三角形的外角的顶点，并将外角的两个邻角平分成两个相等的角，那么这条直线称为该三角形的外角平分线。

这个定理在解决外角问题时非常有用，它保证了外角平分线的存在性，并简化了我们分析与推导相关问题的步骤。

第三个定理是内角平分线定理，它指出：如果一条直线通过一个三角形的内角的顶点，并将内角的两个邻角平分成两个相等的角，那么这条直线称为该三角形的内角平分线。

这个定理与外角平分线定理类似，但是涉及的是三角形的内角。

利用内角平分线定理，我们可以简化三角形内角相关问题的分析过程。

角平分线三个定理在几何学中占据着重要的地位，是研究角度关系和解决几何问题的基础。

它们不仅具有理论意义，还具有广泛的应用价值。

通过深入理解和熟练运用这三个定理，我们能够提高问题解决的效率，并在实际生活中更好地应用几何知识。

1.2文章结构文章结构：本文主要介绍了角平分线的三个定理，分为引言、正文和结论三个部分。

引言部分首先概述了角平分线的意义和应用，以及本文的目的。

CE O D BA21C E DBA 2143C O B A全等三角形专题讲解专题一 全等三角形判别方法的应用专题概说：判定两个三角形全等的方法一般有以下4种： 1．三边对应相等的两个三角形全等（简写成“SSS ”，“边边边”） 2．两边和它们的夹角对应相等的两个三角形全等（简写成“SAS ”，“边角边”） 3．两角和它们的夹边对应相等的两个三角形全等（简写成“ASA ”，“角边角”） 4．两个角和其中一个角的对边对应相等的两个三角形全等（简写成“AAS ”，“角角边”）而在判别两个直角三角形全等时，除了可以应用以上4种判别方法外，还可以应用“斜边、直角边”，即斜边和一条直角边对应相等的两个直角三角形全等（简写成“HL ”, “斜边、直角边”）．也就是说“斜边、直角边”是判别两个直角三角形全等的特有的方法，它仅适用于判别两个直角三角形全等．三角形全等是证明线段相等，角相等最基本、最常用的方法，这不仅因为全等三角形有很多重要的角相等、线段相等的特征，还在于全等三角形能把已知的线段相等、角相等与未知的结论联系起来．那么我们应该怎样应用三角形全等的判别方法呢？（1）条件充足时直接应用在证明与线段或角相等的有关问题时，常常需要先证明线段或角所在的两个三角形全等，而从近年的中考题来看，这类试题难度不大，证明两个三角形的条件比较充分．只要同学们认真观察图形，结合已知条件分析寻找两个三角形全等的条件即可证明两个三角形全等．例1 已知：如图，CE ⊥AB 于点E ，BD ⊥AC 于点D ，BD 、CE 交于点O ，且AO 平分∠BAC ．那么图中全等的三角形有___对．分析：由CE ⊥AB ，BD ⊥AC ，得∠AEO=∠ADO=90º．由AO 平分∠BAC ，得∠EAO=∠DAO ．又AO 为公共边，所以△AEO ≌△ADO ．所以EO=DO ，AE=AD ．又∠BEO=∠CDO=90º，∠BOE=∠COD ，所以△BOE ≌△COD ．由 AE=AD ，∠AEO=∠ADO=90º，∠BAC 为公 共角，所以△EAC ≌DAO ．所以AB=AC ．又∠EAO=∠DAO ， AO 为公共边，所以△ABO ≌△ACO ．所以图中全等的三角形一共有4对．（2）条件不足，会增加条件用判别方法此类问题实际是指条件开放题，即指题中没有确定的已知条件或已知条件不充分，需要补充使三角形全等的条件．解这类问题的基本思路是：执果索因，逆向思维，逐步分析，探索结论成立的条件，从而得出答案．例2 如图，已知AB=AD ，∠1=∠2，要使△ABC ≌△ADE ，还需添加的条件是（只需填一个）_____． 分析：要使△ABC ≌△ADE ，注意到∠1=∠2， 所以∠1+∠DAC=∠2+∠DAC ，即∠BAC=∠EAC ．要使△ABC ≌△ADE ，根据SAS 可知只需AC=AE即可；根据ASA 可知只需∠B=∠D ；根据AAS 可知只需∠C=∠E ．故可添加的条件是AC=AE 或∠B=∠D 或∠C=∠E ．（3）条件比较隐蔽时，可通过添加辅助线用判别方法在证明两个三角形全等时， 当边或角的关系不明显时，可通过添加辅助线作为桥梁，沟通边或角的关系， 使条件由隐变显，从而顺利运用全等三角形的判别方法证明两个三角形全等．例3 已知：如图，AB=AC ，∠1=∠2．求证：AO 平分∠BAC ．GA B F D E C ODA CB 要证∠BAO=∠BCO ，只需证∠BAO 和∠BCO 所在的两个三角形全等．而由已知条件知，只需再证明BO=CO 即可．证明：连结BC ．因为AB=AC ，所以∠ABC ＝∠ACB ．因为∠1=∠2，所以∠ABC -∠1＝∠ACB -∠2． 即∠3=∠4，所以BO=CO ．因为AB=AC ，BO=CO ，AO=AO ， 所以△ABO ≌△ACO ．所以∠BAO=∠CAO ，即AO 平分∠BAC ．（4）条件中没有现成的全等三角形时，会通过构造全等三角形用判别方法有些几何问题中，往往不能直接证明一对三角形全等，一般需要作辅助线来构造全等三角形．例4 已知：在Rt △ABC 中，∠ACB=90º，AC=BC ，D 为BC 的中点，CE ⊥AD 于E ，交AB 于F ，连接DF ．求证：∠ADC=∠BDF ． 证明：过B 作BG ⊥BC 交CF 延长线于G ， 所以BG ∥AC ．所以∠G=∠ACE ．因为AC ⊥BC ， CE ⊥AD ，所以∠ACE=∠ADC ．所以∠G=∠ADC ．因为AC=BC ，∠ACD ＝∠CBG=90º，所以△ACD ≌△CBG ．所以BG=CD=BD ．因为∠CBF=∠GBF=45º，BF=BF ，所以△GBF ≌△DBF ．所以∠G=∠BDF ．所以∠ADC ＝∠BDF ．所以∠ADC ＝∠BDF ．说明：常见的构造三角形全等的方法有如下三种：①涉及三角形的中线问题时，常采用延长中线一倍的方法，构造出一对全等三角形；②涉及角平分线问题时，经过角平分线上一点向两边作垂线，可以得到一对全等三角形；③证明两条线段的和等于第三条线段时，用“截长补短”法可以构造一对全等三角形．（5）会在实际问题中用全等三角形的判别方法新课标强调了数学的应用价值，注意培养同学们应用数学的意识，形成解决简单实际问题的能力﹒在近年中考出现的与全等三角形有关的实际问题，体现了这一数学理念，应当引起同学们的重视．例5 要在湖的两岸A 、B 间建一座观赏桥，由于条件 限制，无法直接度量A ，B 两点间的距离﹒请你用学过的数 学知识按以下要求设计一测量方案﹒(1)画出测量图案﹒(2)写出测量步骤（测量数据用字母表示）(3)计算A 、B 的距离（写出求解或推理过程，结果用字母表示）﹒分析：可把此题转化为证两个三角形全等．第(1)题，测量图案如图5所示．第(2)题，测量步骤：先在陆地上找到一点O ，在AO 的延长线上取一点C ，并测得OC=OA ，在BO 的延长线上取一点D ，并测得OD=OB ，这时测得CD 的长为a ，则AB 的长就是a ．第(3)题易证△AOB ≌△COD ，所以AB=CD ，测得CD 的长即可得AB 的长．解：(1)如右图示．(2)在陆地上找到可以直接到达A 、B 的一点O ，在AO 的延长线上取一点C ，并测得OC ＝OA ，在BO 的延长线上取一点D ，并测得OD ＝OB ，这时测出CD 的长为a ，则AB 的长就是a ．(3)理由：由测法可得OC=OA ，OD=OB ．又∠COD=∠AOB ，∴△COD ≌△AOB ． ∴CD=AB=a ．评注：本题的背景是学生熟悉的，提供了一个学生FCEDBA CEDBAA OQ M CPBN A D C PBHF EGAD CBA学生用数学的意识﹒练习：1．已知：如图，D 是△ABC 的边AB 上一点，AB ∥FC ，DF 交AC 于点E ，DE=FE ． 求证：AE=CE ．2．如图，在△ABC 中，点E 在BC 上，点D 在AE 上，已知∠ABD=∠ACD ，∠BDE=∠CDE ． 求证：BD=CD ．3．用有刻度的直尺能平分任意角吗？下面是一种 方法：如图所示，先在∠AOB 的两边上取OP=OQ ， 再取PM=QN ，连接PN 、QM ，得交点C ，则射线OC 平分∠AOB ．你能说明道理吗？4．如图，△ABC 中，AB=AC ，过点A 作 GE ∥BC ，角平分线BD 、CF 相交于点H ，它们的 延长线分别交GE 于点E 、G ．试在图中找出3对全等三角形，并对其中一对全等三角形给出证明．5．已知：如图，点C 、D 在线段AB 上，PC=PD ．请你添加一个条件，使图 中存在全等三角形，并给予证明．所添条件为__________，你得到的一 对全等三角形是△_____≌△_____．6．如图，∠A=∠D ，BC=EF ，那么需要 补充一个直接条件_____（写出一个即可），才能AD CBAODCBAFCGBEAF DCB E7．如图，在△ABD和△ACD中，AB=AC，∠B=∠C．求证：△ABD≌△ACD．8．如图，直线AD与BC相交于点O，且AC=BD，AD=BC．求证：CO=DO．9．已知△ABC，AB=AC，E、F分别为AB和AC延长线上的点，且BE=CF，EF交BC于G．求证：EG=GF．10．已知：如图，AB=AE，BC=ED，点F是CD的中点，AF⊥CD．求证：∠B=∠E．11．如图，某同学把一把三角形的玻璃打碎成了三块，现在要到玻璃店去配一块大小形状完全一样的玻璃，那么最省事的办法是（）(A)带①和②去 (B)带①去(C)带②去 (D)带③去12．有一专用三角形模具，损坏后，只剩下如图中的阴影部分，你对图中做哪些数据度量后，就可以重新制作一块与原模具完全一样的模具，并43O E DC B A 21F ED C BA 2113．如图，将两根钢条AA'、BB'的中点O 连在一起，使AA'、BB'可以绕着点O 自由转动，就做成了一个测量工件，则A' B'的长等于内槽宽AB ，那么判定△OAB ≌△OAB 的理由是（ ）（A ）边角边 （B ）角边角 （C ）边边边 （D ）角角边专题二 角的平分线从一个角的顶点出发，把一个角分成相等的两个角的射线，叫做这个角的平分线．角的平分线有着重要的作用，它不仅把角分成相等的两部分，而且角的平分线上的点到角两边的距离相等，到一个角的两边距离相等的点在这个角的平分线上，再加上角的平分线所在的直线是角的对称轴．因此当题目中有角的平分线时，可根据角的平分线性质证明线段或角相等，或利用角的平分线构造全等三角形或等腰三角形来寻找解题思路．（1）利用角的平分线的性质证明线段或角相等例6 如图，∠1＝∠2，AE ⊥OB 于E ，BD ⊥OA 于D ，交点为C ．求证：AC=BC ．证法：∵AE ⊥OB ，BD ⊥OA ，∴∠ADC=∠BEC=︒90． ∵∠1＝∠2，∴CD=CE ． 在△ACD 和△BCE 中，∠ADC=∠BEC ，CD=CE ，∠3＝∠4． ∴△ACD ≌△BCE(ASA)，∴AC=BC ．说明：本题若用全等方法证明点C 到OA 、OB 距离相等，浪费时间和笔墨，不如直接应用角平分线性质证明，原因在于同学们已经习惯了用全等的方法，不善于直接应用定理，仍去找全等三角形，结果相当于重新证明了一次定理，以后再学新定理，应用时要注意全等定势的干扰，注意采用简捷证法．例7 已知：如图，△ABC 中，BD=CD ，∠1＝∠2． 求证：AD 平分∠BAC ．证明：过D 作DE ⊥AB 于E ，DF ⊥AC 于F ． 在△BED 与△CFD 中，∠1＝∠2，∠BED ＝∠CFD ＝︒90，BD=CD ，∴△BED ≌△CFD(AAS)．∴DE ＝DF ，∴AD 平分∠BAC ． 说明：遇到有关角平分线的问题时，可引角的两边的垂线，先证明三角形全等，然后根据全等三角形的性质得出垂线段相等，再利用角的平分线性质得出两角相等．（2）利用角的平分线构造全等三角形 ①过角平分线上一点作两边的垂线段例8 如图，AB ∥CD ，E 为AD 上一点，且BE 、CE 分别平分∠ABC 、∠BCD ． 求证：AE=ED ．A FH D CG B EA D CB E A F DC B E CEBA D点E 分别作AB 、BC 、CD 的垂线段．证明：过点E 作EF ⊥AB ，交BA 的延长线于点F ，作EG ⊥BC ，垂足为G ，作EH ⊥CD ，垂足为H ． ∵BE 平分∠ABC ，EF ⊥AB ，EG ⊥BC ， ∴EF=EG ．同理EG =EH ．∴EF=EH ． ∵AB ∥CD ，∴∠FAE=∠D ． ∵EF ⊥AB ，EH ⊥CD ，∴∠AFE=∠DHE=90º．在△AFE 和△DHE 中，∠AFE=∠DHE ，EF=EH ，∠FAE=∠D ． ∴△AFE ≌△DHE ．∴AE=ED ．②以角的平分线为对称轴构造对称图形例9 如图，在△ABC 中，AD 平分∠BAC ，∠C=2∠B ． 求证：AB=AC+CD ．分析：由于角平分线所在的直线是这个角的对称轴，因此在AB 上截取AE=AC ，连接DE ，我们就能构造出一对全等三角形，从而将线段AB 分成AE 和BE 两段，只需证明BE=CD 就可以了．证明：在AB 上截取AE=AC ，连接DE ． ∵AD 平分∠BAC ，∴∠EAD=∠CAD ． 在△EAD 和△CAD 中，∠EAD=∠CAD ，AD=AD ，AE=AC ， ∴△EAD ≌△CAD ．∴∠AED=∠C ，CD=DE ．∵∠C=2∠B ，∴∠AED=2∠B ．∵∠AED=∠B+∠EBD ，∴∠B=∠EDB ． ∴BE=ED ．∴BE=CD ．∵AB=AE+BE ，∴AB=AC+CD ．③延长角平分线的垂线段，使角平分线成为垂直平分线例10 如图，在△ABC 中，AD 平分∠BAC ，CE ⊥AD 于E ． 求证：∠ACE=∠B+∠ECD ．分析：注意到AD 平分∠BAC ，CE ⊥AD ，于是可延长CE 交AB 于点F ， 即可构造全等三角形．证明：延长CE 交AB 于点F ．∵AD 平分∠BAC ，∴∠FAE=∠CAE ． ∵CE ⊥AD ，∴∠FEA=∠CEA=90º．在△FEA 和△CEA 中，∠FAE=∠CAE ，AE=AE ，∠FEA=∠CEA ．∴△FEA ≌△CEA ．∴∠ACE=∠AFE ．∵∠AFE=∠B+∠ECD ，∴∠ACE=∠B+∠ECD ．（3）利用角的平分线构造等腰三角形如图，在△ABC 中，AD 平分∠BAC ，过点D 作DE ∥AB ，DE 交AC 于点E ．易证△AED 是等腰三角形． 因此，我们可以过角平分线上一点作角的一边的平行线， 构造等腰三角形．例11 如图，在△ABC 中，AB=AC ，BD 平分∠ABC ，DE ⊥BD 于D ，交BC 于点E ．求证：CD=21BE ． 1CF E BADQPCBACB AD 然后再证明CD 与这两条线段都相等． 证明：过点D 作DF ∥AB 交BC 于点F ． ∵BD 平分∠ABC ，∴∠1=∠2．∵DF ∥AB ，∴∠1=∠3，∠4=∠ABC ． ∴∠2=∠3，∴DF=BF ．∵DE ⊥BD ，∴∠2+∠DEF=90º，∠3+∠5=90º． ∴∠DEF=∠5．∴DF=EF ． ∵AB=AC ，∴∠ABC=∠C ． ∴∠4=∠C ，CD=DF ． ∴CD=EF=BF ，即CD=21BE ．练习：1．如图，在△ABC 中，∠B=90º， AD 为∠BAC 的平分线，DF ⊥AC 于F ，DE=DC ．求证：BE=CF ．2．已知：如图，AD 是△ABC 的中线，DE ⊥AB 于E ，DF ⊥AC 于F ，且BE=CF ．求证：（1）AD 是∠BAC 的平分线； （2）AB=AC ．3．在△ABC 中，∠BAC=60º，∠C=40º，AP 平分∠BAC 交BC 于P ，BQ 平分∠ABC 交AC 于Q ．求证：AB+BP=BQ+AQ ．4．如图，在△ABC 中，AD 平分 ∠BAC ，AB=AC+CD ．求证：∠C=2∠B ．CEBA D CB AD4321C EBADCEBADCBAD5．如图，E 为△ABC 的∠A 的平分线 AD 上一点，AB ＞AC ．求证：AB -AC ＞EB -EC ．6．如图，在四边形ABCD 中，BC ＞BA ， AD=CD ，BD 平分∠ABC ． 求证：∠A+∠C=180º．7．如图所示，已知AD ∥BC ，∠1=∠2， ∠3=∠4，直线DC 过点E 作交AD 于点D ，交 BC 于点C ．求证：AD+BC=AB ．8．已知，如图，△ABC 中，∠ABC=90º， AB=BC ，AE 是∠A 的平分线，CD ⊥AE 于D ．求证：CD=21AE ．9．△ABC 中，AB=AC ，∠A=100º， BD 是∠B 的平分线．求证：AD+BD=BC ．ACB D ACF E B MD10．如图，∠B 和∠C 的平分线相交于点F ， 过点F 作DE ∥BC 交AB 于点D ，交AC 于点 E ，若BD+CE=9，则线段DE 的长为（ ） A ．9 B ．8 C ．7 D ．611．如图，△ABC 中，AD 平分∠BAC ， AD 交BC 于点D ，且D 是BC 的中点． 求证：AB=AC ．12．已知：如图，△ABC 中，AD 是∠BAC 的平分线， E 是BC 的中点，EF ∥AD ，交AB 于M ， 交CA 的延长线于F ． 求证：BM=CF ．。

三角形的判定大题知识点1、全等三角形的判定边边边：三边对应相等的两个三角形全等（可简写成“SSS”)边角边:两边和它们的夹角对应相等两个三角形全等（可简写成“SAS”)角边角:两角和它们的夹边对应相等的两个三角形全等（可简写成“ASA”)角角边:两角和其中一角的对边对应相等的两个三角形全等（可简写成“AAS”) 斜边.直角边：斜边和一条直角边对应相等的两个直角三角形全等（可简写成“HL”)4、证明两个三角形全等的基本思路：例题精讲---sss例1.如图，，，求证：.例2.如图，AB = DE，AC = DF，BE = CF. 求证：AB∥DE.对应练习3.如图CE=CB，CD=CA，DE=AB，求证：∠DCA=∠ECB4.已知：如图A、F、B、D四点在同一直线上，且AC＝DE，CB＝EF，AF＝DB．求证：∠A＝∠D．例题精讲---ASA例1：.如图，已知：AD是BC上的中线，BE∥CF.求证：DF=DE.对应练习7.如图，点A，C，B，D在同一条直线上，BE∥DF，∠A=∠F，AB=FD，求证：AE=FC.例题精讲--AAS例1.如图，在△ABC中，，，,垂足为，，垂足为.求证：.例2 .如图，△ABC中，AB=AC，点D、E分别在AB、AC的延长线上，且BD=CE，DE与BC相交于点F. 求证：DF=EF.对应练习10：.如图已知：如图，DE⊥AC于点E，BF⊥AC于点F，CD∥AB，AB=CD。

求证：△ABF≌△CDE。

11.已知：如图，∠ABC=90°，AB=BC，CE⊥BE，AD⊥BE，求证：△ABD≌△BCE.例题精讲-SAS例1.如图，已知AC=AD，∠CAB=∠DAB，求证：∠C=∠D。

例2.如图，点B，E，F，C在一条直线上，AB=DC，BE=CF，∠B=∠C．求证：∠A=∠D。

对应练习13.如图，点B、E、C、F在同一条直线上，AB=DE，∠ABC=∠DEF，BE=CF，求证：∠ACB=∠F．例题精讲--HL14.如图，，，，垂足分别为, ，.求证：.15.如图，AB⊥BD，AC⊥CD，垂足分别为点B、C，AB=CD。

线段的垂直平分线----知识讲解(基础)责编：杜少波【学习目标】1.掌握线段的垂直平分线的性质定理及其逆定理，能够利用尺规作已知线段的垂直平分线．2.会证明三角形的三条中垂线必交于一点.掌握三角形的外心性质定理.3.已知底边和底边上的高，求作等腰三角形.4.能运用线段的垂直平分线的性质定理及其逆定理解决简单的几何问题及实际问题．【要点梳理】要点一、线段的垂直平分线1.定义经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线，也叫线段的中垂线．2.线段垂直平分线的做法求作线段AB 的垂直平分线.作法：（1）分别以点A ，B 为圆心，以大于21AB 的长为半径作弧，两弧相交于C ，D 两点； （2）作直线CD ，CD 即为所求直线．要点诠释：(1)作弧时的半径必须大于21AB 的长，否则就不能得到两弧的交点了． (2)线段的垂直平分线的实质是一条直线.要点二、线段的垂直平分线定理线段的垂直平分线定理：线段垂直平分线上的点到这条线段两个端点的距离相等． 要点诠释：线段的垂直平分线定理也就是线段垂直平分线的性质，是证明两条线段相等的常用方法之一．同时也给出了引辅助线的方法，“线段垂直平分线，常向两端把线连”.就是遇见线段的垂直平分线，画出到线段两个端点的距离，这样就出现相等线段，直接或间接地为构造全等三角形创造条件．要点三、线段的垂直平分线逆定理线段的垂直平分线逆定理：到一条线段两个端点距离相等的点，在这条线段的垂直平分线上． 要点诠释：到线段两个端点距离相等的所有点组成了线段的垂直平分线.线段的垂直平分线可以看作是与这条线段两个端点的距离相等的所有点的集合．要点四、三角形的外心三角形三边垂直平分线交于一点，该点到三角形三顶点的距离相等，这点是三角形外接圆的圆心——外心.要点诠释:1.三角形三条边的垂直平分线必交于一点（三线共点），该点即为三角形外接圆的圆心.2.锐角三角形的外心在三角形内部；钝角三角形的外心在三角形外部；直角三角形的外心在斜边上，与斜边中点重合.3.外心到三顶点的距离相等.要点五、尺规作图作图题是初中数学中不可缺少的一类试题，它要求写出“已知，求作，作法和画图”，画图必须保留痕迹，在现行的教材里，一般不要求写出作法，但是必须保留痕迹.证明过程一般不用写出来.最后要点题即“xxx即为所求”.【典型例题】类型一、线段的垂直平分线定理1、如图，△ABC中AC＞BC，边AB的垂直平分线与AC交于点D，已知AC=5，BC=4，则△BCD的周长是（）A．9 B．8 C．7 D．6【思路点拨】先根据线段垂直平分线的性质得到AD=BD，即AD+CD=BD+CD=AC，再根据△BCD 的周长=BC+BD+CD即可进行解答．【答案】A；【解析】因为BD=AD,所以△BCD的周长=BD+CD+BC=AD+CD+BC=5+4=9.【总结升华】此题正是应用了线段垂直平分线的性质定理，也就是已知直线是线段垂直平分线，那么垂直平分线上的点到线段的两个端点距离相等，从而把三角形的边进行转移，进而求得三角形的周长．举一反三：【变式1】如图，在△ABC中，AB=AC，∠A=36°，AB的垂直平分线DE交AC于D，交AB于E，下述结论错误的是（）A．BD平分∠ABC B．△BCD的周长等于AB+BCC．AD=BD=BC D．点D是线段AC的中点【答案】D；提示:根据等边对等角、三角形内角和定理及线段垂直平分线的性质定理即可推得选项A、B、C正确；所以选D,另外，注意排除法在解选择题中的应用．【变式2】（2015秋•江阴市校级月考）如图，△ABC中，BC=7，AB的垂直平分线分别交AB、BC于点D、E，AC的垂直平分线分别交AC、BC于点F、G．求△AEG的周长．【答案】解：∵DE为AB的中垂线，∴AE=BE，∵FG是AC的中垂线，∴AG=GC，△AEG的周长等于AE+EG+GA，分别将AE和AG用BE和GC代替得：△AEG的周长等于BE+EG+GC=BC，所以△AEG的周长为BC的长度即7．类型二、线段的垂直平分线的逆定理2、如图，已知AB=AC,∠ABD=∠ACD，求证：AD是线段BC的垂直平分线．A【答案与解析】证明：∵ AB=AC（已知）∴∠ABC=∠ACB (等边对等角)又∵∠ABD=∠ACD (已知)∴∠ABD-∠ABC =∠ACD-∠ACB (等式性质)即∠DBC=∠DCB∴DB=DC （等角对等边）∵AB=AC（已知）DB=DC（已证）∴点A和点D都在线段BC的垂直平分线上（和一条线段两个端点距离相等的点，在这条线段的垂直平分线上）∴AD是线段BC的垂直平分线。

第六节角平分线的性质与判定中考考点分析在教材中的地位重点、难点角平分线的性质与判定在考试中常出现在综合题中，需要学生根据实际情况作辅助线来帮助分析。

角平分线的性质在教材中位于全等三角形章节的最后一节，角平分线的三种常用辅助线的作法涉及全等三角形的5个判定，角平分线的性质能够帮助学生简化书写步骤。

角平分线的判定为学生提供了另一种证明角相等的方法。

理解并熟练掌握角平分线的性质与角平分线的判定。

通过角平分线的三种常用辅助线的训练，熟悉推理证明的思路方法和书写格式，培养和提高逻辑思维能力。

讲点1 角平分线的性质例1如图，AD是△ABC的平分线，DE⊥AB交AB于点E，DF⊥AC交AC于点F，若SABC△＝7，DE＝2，AB＝4，则AC的值为（）（2013，硚口区期中）A. 4B. 3C. 6D. 5题意分析根据角平分线性质可得DE＝DF，AD将△ABC的面积分成两部分，DE，DF分别为这两部分的高，巧妙地求出AC的长。

解答过程：解题后的思考：练1.1如图，已知△ABC中，AB＝10，BC＝15，CA＝20，若点O是△ABC内角平分线的交点，则△ABO，△BCO，△CAO的面积比是________________。

练1.2如图，BD是∠ABC的平分线，AB＝BC，点E在BD上，连接AE，CE，DF⊥AE，DG⊥CE，垂足分别是F，G，求证：DF＝DG。

（2013，江汉区期中）讲点2 角平分线的判定例2如图，已知BE＝CF，BF⊥AC于点F，CE⊥AB于点E，BF和CE交于点D。

求证：AD平分∠BAC.题意分析要证AD平分∠BAC，若证得DE＝DF，问题就可以解决，因此先证DE＝DF。

证明两个角相等除了利用平行线截得的同位角和内错角、全等三角形的对应角、等腰三角形两底角之外，角平分线的判定也是常用方法，应注意灵活掌握。

解答过程：解题后的思考：练2.1如图，在△ABC中，AC＝AB，点D在BC上，若DE⊥AB于点E，DF⊥AC于点F，DF⊥DE，求证：AD⊥BC。

海伊教育学科教师辅导讲义学员编号：年级：八年级课时数：学员姓名：辅导科目：数学学科教师：高老师课题垂直平分线与角平分线授课时间：2013 年10月25日备课时间：2013 年10月23日教学目标1．经历线段垂直平分线性质的发现过程，初步掌握线段垂直平分线的性质定理及其逆定理，体会辨证思想；2．能运用线段垂直平分线性质定理及其逆定理解决简单的几何问题；3．通过从操作实验到演绎推理的数学活动，认识实验归纳和演绎推理的作用4、掌握角平分线的性质定理和判定定理，并能灵活应用它们进行计算和证明。

5、能够证明角平分线的性质定理和判定定理。

6、能够利用尺规作图作已知角的角平分线。

重点、难点重点：1.线段垂直平分线性质定理及其逆定理；2.2角平分线性质定理和判定定理的应用1世纪教育网难点：1.线段垂直平分线性质定理及其逆定理的应用2. 角平分线性质定理和判定定理的证明及应用。

授课方法联想质疑——交流研讨——归纳总结——实践提高教学过程一、情景设置（知识导入）二、探索研究【知识点总结与归纳】（一）探究新知1.线段的垂直平分线的性质定理操作：以直线MN为折痕将这个图形翻折，观察点P的位置动不动？点A与点B是否重合？你得到哪些线段相等？21世纪教育网归纳：如果一个点在一条直线的垂直平分线上，那么分别联结这点与线段两个端点所得的两BACDDABCPED ABC ACDB条线段相等.验证：证明这个命题，写出已知和求证.已知：如图，直线MN 是线段AB 的垂直平分线，垂足为点C ，点P 在直线MN 上. 求证： P A ＝PB . [来源:21世纪教育网]分析：如图，当点P 不在线段AB 上时，要证明P A ＝PB ，只需要证△PCA ≌△PCB .由直线MN 是线段AB 的垂直平分线，可知CA =CB ，∠PCA =∠PCB ，再加上PC 为公共边，三角形全等即可得到.21世纪特别地，当点P 在线段AB 上时，P 点与C 点重合，此时PA=PB 当然也成立。

第六节：角平分线与线段的垂直平分线【知识要点归纳 】1、线段垂直平分线的性质线段垂直平分线上的点到这条线段两个端点的距离相等. 2、线段垂直平分线性质定理的逆定理到一条线段两个端点距离相等的点在这条线段的垂直平分线上. 3、关于三角形三边垂直平分线的定理三角形三边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等. 4、角平分线的性质定理：角平分线上的点到这个角的两边的距离相等. 5、角平分线性质定理的逆定理：在角的内部，且到角的两边距离相等的点在这个角的角平分线上. 6、关于三角形三条角平分线的定理：三角形三条角平分线相交于一点，并且这一点到三边的距离相等.【典例讲解】例1 如图1，在△ABC 中，BC ＝8cm ，AB 的垂直平分线交AB 于点D ，交边AC 于点E ，△BCE 的周长等于18cm ，则AC 的长等于（ ） A ．6cm B ．8cm C ．10cm D ．12cm针对性练习：已知：1)如图，AB=AC=14cm,AB 的垂直平分线交AB 于点D ，交AC 于点 E ，如果△EBC 的周长是24cm ，那么BC= 2) 如图，AB=AC=14cm,AB 的垂直平分线交AB 于点D ，交AC 于点E ，如果BC=8cm ，那么△EBC 的周长是3） 如图，AB=AC,AB 的垂直平分线交AB 于点D ，交AC 于点E ， 如果∠A=28度，那么∠EBC 是例2、如图8，已知AD 是△ABC 的BC 边上的高，且∠C ＝2∠B ，求证：BD ＝AC ＋CD.BCD EA 图8BCD A例3、如图10，已知在直角梯形ABCD 中，AB ∥CD ，AB ⊥BC ，E 为BC 中点，连接AE 、DE ，DE 平分∠ADC ，求证：AE 平分∠BAD.【课堂检测】1. 如右图，已知BE ⊥AC 于E ，CF ⊥AB 于F ，BE 、CF 相交于点D ，若BD =CD .求证：AD 平分∠BAC .2. 如图所示，直线l l l 123，，表示三条互相交叉的公路，现在要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有（ ）A. 一处B. 二处C. 三处D. 四处3．在△ABC 中，AB=AC ，∠A=120°，AB 的垂直平分线MN 分别交BC 、AB 于点M 、N. 求证：CM=2BM.4.如图7，在△ABC 中，AC ＝23，AB 的垂直平分线交AB 于点D ，交BC 于点E ，△ACE 的周长为50，求BC 边的长.5.如图11-1，已知在四边形ABCD 中，对角线BD 平分∠ABC ，且∠BAD 与∠BCD 互补，求证：AD ＝CD.图10FCD BAE图7EDACBl 3 l 1l 2。

角平分线和线段的垂直平分线一、知识点讲解：1. 定理1：在角的平分线上的点到这个角的两边的距离相等；定理2：在一个角的内部，到这个角的两边距离相等的点，在这个角的平分线上。

2.角平分线另一种定义：角的平分线是到角的两边距离相等的所有点的集合。

3.在两个命题中，如果第一个命题的题设是第二个命题的结论，而第一个命题的结论又是第二个命题的题设。

那么这两个命题叫做互逆命题，其中一个叫做另一个的逆命题。

4.如果一个定理的逆命题是经过证明的真命题，那么它也是一个定理，这两个定理叫互逆定理。

其中一个叫另一个的逆定理，虽然一个命题都有逆命题，但一个定理并不都有逆定理。

5.定理：线段垂直平分线上的点和这条线段两个端点的距离相等。

逆定理：和一条线段两个端点距离相等的点，在这条线段的垂直平分线上。

6.线段的垂直平分线另一种定义：线段的垂直平分线可以看作和线段两个端点距离相等的所有点的集合。

二、例题精讲例1.已知如图，在ΔABC中，AD是∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，求证：AD⊥EF。

分析：欲证AD⊥EF，就要证∠AOE=∠AOF=∠EOF=90°。

所以要考虑证ΔAEO≌ΔAFO。

由题中条件可知ΔAEO，ΔAFO已有一边（公共边）一角对应相等，只要证出AE=AF问题就解决了，所以需先证明ΔAED≌ΔAFD。

证明：∵AD是∠BAC的平分线，DE⊥AB，DF⊥AC（已知）∴DE=DF（角平分线上的点到这个角的两边距离相等）在RtΔAED和RtΔAFD中∴RtΔAED≌RtΔAFD(HL), ∴AE=AF(全等三角形的对应边相等)在ΔAEO和ΔAFO中∴ΔAEO≌ΔAFO,∴∠AOE=∠AOF (全等三角形对应角相等)∴∠AOE=∠EOF=90°，∴AD⊥EF（垂直定义）。

例2.写出下列定理的逆命题，并判断真假。

(1)同位角相等，两直线平行。

(2)如果x=3，那么x2=9.(3)如果ΔABC是直角三角形，那么当每个内角取一个对应外角时，ΔABC的三个外角中只有两个钝角。

基本内容 线段的垂直平分线及角的平分线知识精要一、线段的垂直平分线1、线段的垂直平分线定理：线段的垂直平分线上的任意一点到这条线段两个端点的距离相等。

2、线段的垂直平分线逆定理：和一条线段两个端点距离相等的点，在这条线段的垂直平分线上。

二、角的平分线1、角平分线定理：角平分线上的点到这个角的两边的距离相等。

2、角平分线逆定理：在一个角的内部（包括顶点）且到这个角的两边距离相等的点，在这个角的平分线上。

3、角平分线可以看作是在这个角内部（包括顶点）到角两边的距离相等的点的集合 提问：在使用角平分线的性质定理及其逆定理时，应注意哪些方面？ 回答：必须有两个垂直的条件，若缺少垂直条件时，可考虑添加辅助线；热身练习1、如图，在△ABC 中，AB=AC,AB 的垂直平分线DE 交BC 于点D,且DC=AC,求△ABC 各角的大小.解：108,36A B C ∠=︒∠=∠=︒；2、如图，在△ABC 中，AB=AC ，AD 是中线，且DE ⊥AB ，DF ⊥AC ， 求证：BE=CF证明：因为AB=AC ，AD 是中线 所以BD=DC ，∠B=∠C ，AD 是角平分线， 因为DE ⊥AB ，DF ⊥AC 所以DE=DF所以BDE CDF ∆≅∆ 所以BE=FC3、如图△ABC 的外角平分线∠DBC 、∠ECB 的平分线相交于点F ，求证：点F 在∠A 的平分线上ADCAB CDEF证明：过F 作AE 的垂线交于点M ，作AD 的垂 线交于点N ，作BC 的垂线交于点O 因为CF 是∠ECB 平分线，所以MF=FO因为FB 是∠DBC 平分线，所以NF=FO 所以MF=NF ，又因为MF 垂直AE ，NF 垂直AD 所以AF 是∠A 的平分线4、 如图，过△ABC 的边BC 的中点M ，作直线平行于∠A 的平分线AA ′，而交直线AB 于E 、F ，求证：CF=1/2(AB+AC)证明：延长FM 到点G ，使FM=MG ，连接BG ∵M 为BC 的中点 ∴BMG CMF ∆≅∆ ∴BG=CF 又∵AA’平分∠BAC 且EM// AA’∴''E BAA A AF AFE CFG G ∠=∠=∠=∠=∠=∠ ∴AE=AF ，BE=BG=CF ∵BE=AB+AE,CF=AC-AF ∴AB+AC=BE+CF=2CF ∴CF=1/2(AB+AC)5、如图，求作点P ，使P 到C 、D 的距离相等，同时到角两边的距离也相等 解：先作线段DC 的垂直平分线，再作∠A 的平分线， 两直线所交的点即为点P精解名题ABCDEF例1、如图，AD 是△ABC 的角平分线，EF 是AD 的中垂线， 求证：（1）∠EAD=∠EDA ；（2）DF ∥AC ；（3）∠EAC=∠B证明：（1）因为EF 是AD 的中垂线所以AE=DE ，所以∠EAD=∠EDA （2）因为EF 是 AD 的中垂线，所以FA=FD 所以∠FAD=∠FDA 又因为AD 是角平分线，所以∠FAD=∠DAC所以∠FDA=∠DAC ，所以DF ∥AC （3）因为∠EDA=∠B+∠BAD ；∠EAD=∠EAC+∠DAC又因为∠EAD=∠EDA ，∠BAD=∠DAC ；所以∠B=∠EAC ；例2、AP 、BP 分别平分∠DAB 、∠CBA,PM ⊥AD 于点M,PN ⊥BC 于点N, 求证：点P 在线段MN 的垂直平分线上. 证明：过点P 作PE ⊥AB 于点E ，连接MN∵AP 平分∠DAB ∴PM=PE ∵BP 平分∠CBA ∴PE=PN ∴PM=PN∴点P 在线段MN 的垂直平分线上例3、如图, 在△ABC 中，点D 、E 分别在AC 、AB 上，BM 平分∠ABC ，CM 平分∠ACB ，EN 平分∠BED ，DN 平分∠EDC 。