线段垂直平分线和角平分线(经典)

3.线段的垂直平分线4.角平分线例1：（1）在△ABC中，AB＝AC，AB的垂直平分线交AB于N，交BC的延长线于M，∠A＝，求∠NMB的大小（2）如果将（1）中∠A的度数改为，其余条件不变，再求∠NMB的大小（3）你发现有什么样的规律性？试证明之.（4）将（1）中的∠A改为钝角，对这个问题规律性的认识是否需要加以修改例2：在△ABC中，AB的中垂线DE交AC于F，垂足为D，若AC=6，BC=4，求△BCF 的周长。

例3：如图所示，AC=AD，BC=BD，AB与CD相交于点E。

求证：直线AB是线段CD的垂直平分线。

例4：如图所示，在△ABC中，AB=AC，∠BAC=1200，D、F分别为AB、AC的中点，，E、G在BC上，BC=15cm，求EG的长度。

例5:：如图所示，Rt△ABC中，，D是AB上一点，BD=BC，过D作AB的垂线交AC于点E，CD交BE于点F。

求证：BE垂直平分CD。

例6:：在⊿ABC中，点O是AC边上一动点，过点O作直线MN∥BC，与∠ACB的角平分线交于点E，与∠ACB的外角平分线交于点F，求证：OE=OF例7、如图所示，AB>AC，的平分线与BC的垂直平分线相交于D，自D作于E，，求证：BE=CF。

答案如下：例1：解：（1）∵∠B= 1/2（180°-∠A）=70°，∴∠M=20°；（2）同理得，∠M=35°；（3）规律是：∠M的大小为∠A大小的一半，即：AB的与底边BC所夹的等于∠A的一半．证明：设∠A=α，则有∠B= 1/2（180°-α），∠M=90°- 1/2（180°-α）= 1/2α．（4）改为后规律成立．上述规律为：等腰三角形一腰的与底边相交所成的等于顶角的一半．例2：解：连接BF，由线段的垂直平分线的性质可得，FB＝FA又因为AC＝AF+CF＝6，所以BF+CF＝6△BCF的周长＝BC+CF+BF＝4+6＝10例3：证明：因为AC=AD所以A在线段CD的上又因为BC=BD所以B在线段CD的上所以直线AB是线段CD的例4：解：作AH⊥BC于H，HC=15/2∵等腰∴∠ACB=∠ABC=30°∴AC=2EC/根号3EC=5根号3∵F为AC中点∴FC=5/2根号3∵FG⊥AC∴CG=5同理，BE=5∴EG=5例5：证明：∵DE⊥AB，∠ACB＝90∴∠BDE＝∠ACB＝90∵BD＝BC，BE＝BE∴△BCE≌△BDE （HL）∴∠CBE＝∠DBE∵BF＝BF∴△BCF≌△BDF （SAS）∴∠BFC＝∠BFD，CF＝DF∵∠BFC+∠BFD＝180∴∠BFC＝∠BFD＝90∴BE⊥CD∴BE垂直平分CD例6：解：∵MN∥BC，∴∠OEC=∠BCE，∠OFC=∠GCF，又已知CE平分∠BCO，CF平分∠GCO，∴∠OCE=∠BCE，∠OCF═∠GCF，∴∠OCE=∠OEC，∠OCF=∠OFC，∴EO=CO，FO=CO，∴EO=FO．例7：证明：连接DC，DB∵点D在BC的垂直平分线上∴DB=DC∵D在∠BAC的平分线上∴DE=DF∵∠DFC=∠DEB∴△DCF≌△DEB∴CF=BE。

一、知识点讲解：1. 定理1：在角的平分线上的点到这个角的两边的距离相等；定理2：在一个角的内部，到这个角的两边距离相等的点，在这个角的平分线上。

2.角平分线另一种定义：角的平分线是到角的两边距离相等的所有点的集合。

3.在两个命题中，如果第一个命题的题设是第二个命题的结论，而第一个命题的结论又是第二个命题的题设。

那么这两个命题叫做互逆命题，其中一个叫做另一个的逆命题。

4.如果一个定理的逆命题是经过证明的真命题，那么它也是一个定理，这两个定理叫互逆定理。

其中一个叫另一个的逆定理，虽然一个命题都有逆命题，但一个定理并不都有逆定理。

5.定理：线段垂直平分线上的点和这条线段两个端点的距离相等。

逆定理：和一条线段两个端点距离相等的点，在这条线段的垂直平分线上。

6.线段的垂直平分线另一种定义：线段的垂直平分线可以看作和线段两个端点距离相等的所有点的集合。

二、例题精讲例1.已知如图，在ΔA BC中，AD是∠BA C的平分线，DE⊥A B于E，DF⊥A C于F，求证：AD⊥EF。

分析：欲证AD⊥EF，就要证∠AOE=∠AOF=∠EOF=90°。

所以要考虑证ΔA EO≌ΔAFO。

由题中条件可知ΔA EO，ΔAFO已有一边（公共边）一角对应相等，只要证出A E=AF问题就解决了，所以需先证明ΔA ED≌ΔAFD。

证明：∵A D是∠BA C的平分线，DE⊥AB，DF⊥A C（已知）∴DE=DF（角平分线上的点到这个角的两边距离相等）在RtΔAED和RtΔAFD中∴RtΔA ED≌RtΔAFD(HL), ∴A E=AF(全等三角形的对应边相等)在ΔA EO和ΔAFO中∴ΔAEO≌ΔAFO,∴∠AOE=∠AOF (全等三角形对应角相等)∴∠A OE=∠EOF=90°，∴AD⊥EF（垂直定义）。

例2.写出下列定理的逆命题，并判断真假。

(1)同位角相等，两直线平行。

(2)如果x=3，那么x2=9.(3)如果ΔABC是直角三角形，那么当每个内角取一个对应外角时，ΔA BC的三个外角中只有两个钝角。

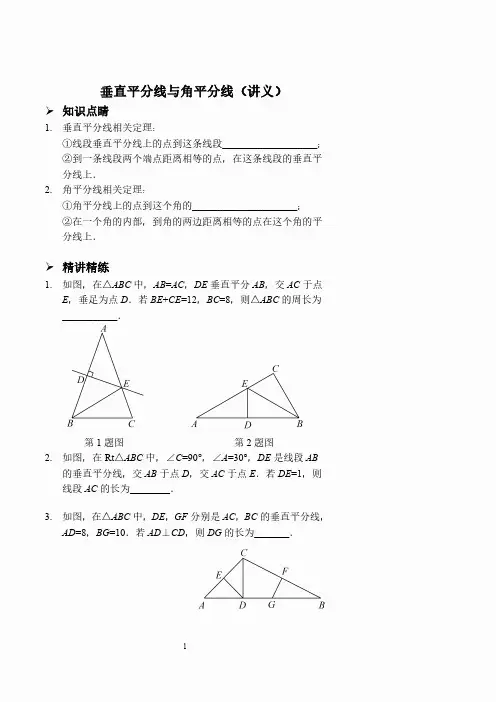
垂直平分线与角平分线（讲义）知识点睛1.垂直平分线相关定理：①线段垂直平分线上的点到这条线段___________________；②到一条线段两个端点距离相等的点，在这条线段的垂直平分线上．2.角平分线相关定理：①角平分线上的点到这个角的_____________________；②在一个角的内部，到角的两边距离相等的点在这个角的平分线上．精讲精练1.如图，在△ABC中，AB=AC，DE垂直平分AB，交AC于点E，垂足为点D．若BE+CE=12，BC=8，则△ABC的周长为___________．第1题图第2题图2.如图，在Rt△ABC中，∠C=90°，∠A=30°，DE是线段AB的垂直平分线，交AB于点D，交AC于点E．若DE=1，则线段AC的长为________．3.如图，在△ABC中，DE，GF分别是AC，BC的垂直平分线，AD=8，BG=10．若AD⊥CD，则DG的长为_______．4.如图，AD与BC相交于点O，OA=OC，∠A=∠C，BE=DE．求证：OE垂直平分BD．5.如图，BD平分∠ABC，DE⊥AB于点E，AB=8，BC=6．若S△ABC=14，则DE=__________．第5题图第6题图6.如图，PC⊥OA于点C，PD⊥OB于点D，且PC=PD，点E在射线OA上，若∠AOB=60°，∠OPE=80°，则∠AEP的度数为_________．7.如图，在△ABC中，∠ABC的平分线与∠ACB的平分线相交于点O，OD⊥AB，OE⊥AC，垂足分别为点D，E．求证：OD=OE．8.已知：如图，△ABC的外角∠CBD和∠BCE的平分线相交于点F，求证：点F在∠DAE的平分线上．9.如图，直线y=x+4与x轴、y轴分别交于点A，B，点C在x轴正半轴上，且OC=OB，点D位于x轴上点C的右侧，连接BC，∠BAO和∠BCD的平分线AP，CP相交于点P，连接BP，则∠PBC的度数为__________．10.如图，在Rt△ABC中，∠C=90°，在AC和AB上分别截取AE，AD，使AE=AD．再分别以点D，E为圆心，大于12 DE的长为半径作弧，两弧在∠BAC内交于点F，作射线AF交边BC于点G．若CG=4，AB=10，则△ABG的面积为________．第10题图第11题图11.如图，在△ABC中，∠B=35°，∠ACB=75°，请依据尺规作图的痕迹，计算∠α=__________．12.过直线上一点，作已知直线的垂线．已知：A为直线MN上一点．求作：直线AB，使AB⊥MN．作法：①以点A为圆心，任意长为半径作弧，交直线MN于C，D两点；②分别以______，______为圆心，_________为半径作弧，两弧交MN上方于一点B；③______________．______________即为所求．13.过直线外一点，作已知直线的垂线．已知：A为直线MN外一点．求作：直线AB，使AB⊥MN．作法：①在MN下方任取一点P；②以_____为圆心，______为半径作弧，交MN于C，D两点；③分别以______，______为圆心，_________为半径作弧，两弧交MN下方于一点B；④______________．______________即为所求．14.如图，已知△ABC，求作：（不写作法，保留作图痕迹）（1）AC边上的高；（2）BC边上的高．15.如图，C，D是∠AOB内部两点，在∠AOB内部求作一点P，使PC=PD，并且使点P到∠AOB两边的距离相等．（不写作法，保留作图痕迹）16.已知：如图，∠ABC，点D在射线BC上．求作：等腰△PBD，使线段BD为等腰△PBD的底边，点P 在∠ABC内部，且点P到∠ABC两边的距离相等．（不写作法，保留作图痕迹）17.如图，A，B是平面上的两定点，在平面上找一点C，使△ABC是以点C为直角顶点的等腰直角三角形，这样的点C有几个？请用尺规作图确定点C的位置，保留作图痕迹．【参考答案】课前预习1.①两个端点的距离相等2.①两边的距离相等精讲精练1.322.33.64.证明略；提示：证△AOB≌△COD（ASA），得到OB=OD，再结合BE=DE，由“到一条线段两个端点距离相等的点，在这条线段的垂直平分线上”得证5.26.110°7.证明略；提示：由“角平分线上的点到这个角的两边的距离相等”可证OD=OF=OE8.证明略；提示：过点F分别作FG⊥AD于G，FH⊥AE于H，FK⊥BC 于K，先由“角平分线上的点到这个角的两边的距离相等”可证FG=FK=FH，再由“在一个角的内部，到角的两边距离相等的点在这个角的平分线上”求证9.45°10.2011.75°12.①点C；点D；大于1CD的长；③作直线AB；直线AB213.②点A；AP长；③点C；点D；大于1CD的长；③作直线2AB；直线AB14.作图略提示：过直线外一点作已知直线的垂线；15.作图略提示：作线段CD的垂直平分线和∠AOB的角平分线；16.作图略提示：作线段BD的垂直平分线和∠ABC的角平分线；17.这样的点C有2个，作图略。

知识要点详解1、线段垂直平分线的性质（1）垂直平分线性质定理：线段垂直平分线上的点到这条线段两个端点的距离相等.定理的数学表示：如图1，已知直线m 与线段AB 垂直相交于点D ，且AD ＝BD ，若点C 在直线m 上，则AC ＝BC.定理的作用：证明两条线段相等 （2）线段关于它的垂直平分线对称.2、线段垂直平分线性质定理的逆定理（1）线段垂直平分线的逆定理：到一条线段两个端点距离相等的点在这条线段的垂直平分线上.定理的数学表示：如图2，已知直线m 与线段AB 垂直相交于点D ，且AD ＝BD ，若AC ＝BC ，则点C 在直线m 上.定理的作用：证明一个点在某线段的垂直平分线上.3、关于三角形三边垂直平分线的定理（1）关于三角形三边垂直平分线的定理：三角形三边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等.定理的数学表示：如图3，若直线,,i j k 分别是△ABC 三边AB 、BC 、CA 的垂直平分线，则直线,,i j k 相交于一点O ，且OA ＝OB ＝OC.定理的作用：证明三角形内的线段相等.（2）三角形三边垂直平分线的交点位置与三角形形状的关系：若三角形是锐角三角形，则它三边垂直平分线的交点在三角形内部；若三角形是直角三角形，则它三边垂直平分线的交点是其斜边的中点；若三角形是钝角三角形，则它三边垂直平分线的交点在三角形外部.反之，三角形三边垂直平分线的交点在三角形内部，则该三角形是锐角三角形；三角形三边垂直平分线的交点在三角形的边上，则该三角形是直角三角形；三角形三边垂直平分线的交点在三角形外部，则该三角形是钝角三角形.图1图2经典例题：例1 如图1，在△ABC 中，BC ＝8cm ，AB 的垂直平分线交AB 于点D ，交边AC 于点E ，△BCE 的周长等于18cm ，则AC 的长等于（ ）A ．6cmB ．8cmC ．10cmD ．12cm课堂笔记：针对性练习：：1)如图，AB=AC=14cm,AB 的垂直平分线交AB 于点D ，交AC 于点 E ，如果△EBC 的周长是24cm ，那么BC= 2) 如图，AB=AC=14cm,AB 的垂直平分线交AB 于点D ，交AC 于点E ，如果BC=8cm ，那么△EBC 的周长是3） 如图，AB=AC,AB 的垂直平分线交AB 于点D ，交AC 于点E ，如果∠A=28 度，那么∠EBC 是例2. 已知： AB=AC ，DB=DC ，E 是AD 上一点，求证：BE=CE 。

沪教版八年级第一学期角平分线角平分线性质定理：角平分线上的点到这个角两边的距离相等。

角平分线的判定： 到一个叫两边的距离相等的点在这个角的平分线上。

例1．如图，在ABC △中，90C ∠=，AD 平分CAB ∠，8cm 5cm BC BD ==，，那么D 点到直线AB 的距离是 cm ．例2．如图，已知在Rt △ABC 中，∠C =90°, BD 平分∠ABC , 交AC 于D .(1) 若∠BAC =30°, 则AD 与BD 之间有何数量关系，说明你的理由; (2) 若AP 平分∠BAC ，交BD 于P , 求∠BPA 的度数.3、考点深入练习例3：如图：在△ABC 中，BE 、CF 分别是AC 、AB 两边上的高，在BE 上截取BD=AC ，在CF 的延长线上截取CG=AB ，连结AD 、AG 。

求证：（1）AD=AG ，（2）AD 与AG 的位置关系如何。

BPABCD GHFEDCBA例4：两个大小不同的等腰直角三角形三角板如图1所示放置，图2是由它抽象出的几何图形，B，C，E在同一条直线上，连结DC．（8分）（1）请找出图2中的全等三角形，并给予证明（说明：结论中不得含有未标识的字母）；（2）证明：DC⊥BE图1 图2例5:△DAC, △EBC均是等边三角形，AE,BD分别与CD,CE交于点M,N.求证：（1）AE=BD (2)CM=CN (3) △CMN为等边三角形（4）MN∥BCC B垂直平分线的性质与判定强化练习1如图1，在△ABC 中，BC ＝8cm ，AB 的垂直平分线交AB 于点D ，交边AC 于点E ，△BCE 的周长等于18cm ，则AC 的长等于 （ ） A ．6cm B ．8cm C ．10cm D ．12cm2题2如图，在Rt ABC △中，90ACB D E ∠=，，分别为AC AB ，的中点，连DE CE ，． 下列结论中不一定正确的是 （ ） A ．ED BC ∥B ．ED AC ⊥C ．ACE BCE ∠=∠D ．AE CE =3、△ABC 中，∠C=90°，AB 的中垂线交直线BC 于D ，若∠BAD －∠DAC=22.5°，则∠B 等于 （ ） A.37.5° B.67.5° C.37.5°或67.5° D.无法确定4、线段的垂直平分线上的点_____________________________________．5、到一条线段的两个端点的距离相等的点，______________________．6、如图，在△ABC 中，AC 的垂直平分线交AC 于E ，交BC 于D ，△ABD 的周长是12 cm ，AC=5cm ，则AB+BD+AD= cm ；AB+BD+DC= cm ；△ABC 的周长是 cm 。

垂直平分线与角平分线精讲教案第一章：垂直平分线的概念与性质1.1 垂直平分线的定义解释线段垂直平分线的概念强调线段垂直平分线上的点到线段两端点的距离相等的性质1.2 垂直平分线的性质展示线段垂直平分线的基本性质引导学生通过几何证明来理解垂直平分线的性质1.3 垂直平分线的作图教授如何作出线段的垂直平分线的方法让学生通过实际操作来加深对垂直平分线作图方法的理解第二章：角平分线的概念与性质2.1 角平分线的定义解释角平分线的概念强调角平分线上的点到角的两边的距离相等的性质2.2 角平分线的性质展示角平分线的基本性质引导学生通过几何证明来理解角平分线的性质2.3 角平分线的作图教授如何作出角的平分线的方法让学生通过实际操作来加深对角平分线作图方法的理解第三章：垂直平分线与角平分线的交点3.1 垂直平分线与角平分线的交点性质解释垂直平分线与角平分线的交点（即内心）的性质强调内心到角的两边的距离相等的性质3.2 垂直平分线与角平分线的交点的应用展示如何利用内心解决几何问题引导学生通过实际问题来应用内心性质解决问题第四章：垂直平分线与角平分线在几何中的应用4.1 利用垂直平分线与角平分线证明线段相等教授如何利用垂直平分线与角平分线证明线段相等让学生通过实际操作来加深对证明方法的理解4.2 利用垂直平分线与角平分线证明角度相等教授如何利用垂直平分线与角平分线证明角度相等让学生通过实际操作来加深对证明方法的理解4.3 利用垂直平分线与角平分线解决实际问题展示如何利用垂直平分线与角平分线解决实际问题引导学生通过实际问题来应用垂直平分线与角平分线性质解决问题第五章：线段垂直平分线的几何作图与应用5.1 线段垂直平分线的作图方法复习线段垂直平分线的作图技巧通过实际操作演示和练习，让学生熟练掌握作图方法5.2 线段垂直平分线在几何作图中的应用介绍线段垂直平分线在解决几何作图问题中的应用通过具体例子展示如何利用线段垂直平分线构造特殊图形或证明几何性质第六章：角平分线的几何作图与应用6.1 角平分线的作图方法教授角平分线的作图方法通过练习让学生掌握角平分线的作图技巧6.2 角平分线在几何作图中的应用探讨角平分线在几何作图中的作用举例说明如何利用角平分线构造特殊图形或证明几何性质第七章：垂直平分线与角平分线在实际问题中的应用7.1 线性规划问题中的应用介绍如何利用垂直平分线与角平分线解决线性规划问题通过实际案例分析，让学生理解几何方法在解决实际问题中的应用7.2 几何证明问题中的应用展示垂直平分线与角平分线在几何证明中的重要性引导学生运用这些线段的性质解决复杂的几何证明问题第八章：垂直平分线与角平分线的综合练习8.1 综合练习题设计设计一系列综合练习题，涵盖垂直平分线与角平分线的知识点确保练习题难度层次分明，适合不同水平的学生8.2 学生练习与反馈监督学生完成练习题，提供必要的帮助和指导收集学生练习结果，分析错误原因，给予针对性的反馈第九章：垂直平分线与角平分线的拓展学习9.1 拓展阅读材料提供关于垂直平分线与角平分线的拓展阅读材料鼓励学生阅读这些材料，以加深对相关概念和应用的理解9.2 研究性学习项目设计一个研究性学习项目，让学生深入研究垂直平分线与角平分线的某个方面指导学生进行研究，帮助他们在探究中学习和思考第十章：总结与评价10.1 知识点回顾与学生一起回顾本教案中的关键概念和定理强调垂直平分线与角平分线在几何学中的重要性10.2 学生评价对学生在整个教案学习过程中的表现进行评价收集学生对教案的反馈，以改进未来的教学设计和内容安排重点和难点解析：一、垂直平分线的作图方法：学生往往对如何准确作出线段的垂直平分线感到困惑，需要通过多次练习和讲解来掌握。

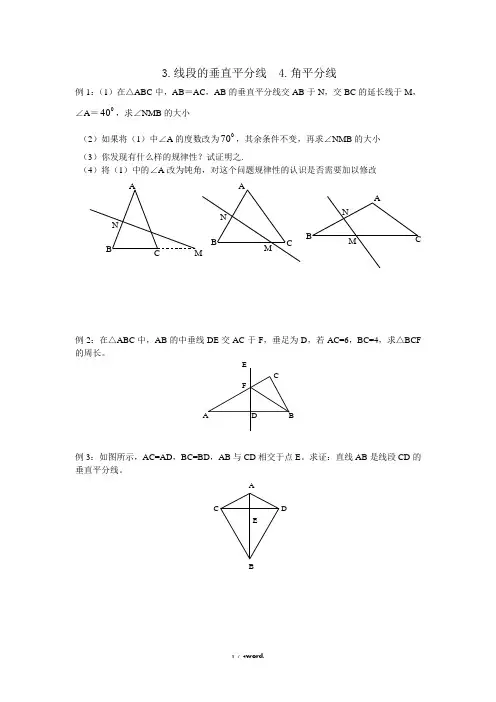
3.线段的垂直平分线4.角平分线例1：（1）在△ABC 中，AB ＝AC ，AB 的垂直平分线交AB 于N ，交BC 的延长线于M ，∠A ＝040，求∠NMB 的大小（2）如果将（1）中∠A 的度数改为070，其余条件不变，再求∠NMB 的大小（3）你发现有什么样的规律性？试证明之.（4）将（1）中的∠A 改为钝角，对这个问题规律性的认识是否需要加以修改例2：在△ABC 中，AB 的中垂线DE 交AC 于F ，垂足为D ，若AC=6，BC=4，求△BCF 的周长。

例3：如图所示，AC=AD ，BC=BD ，AB 与CD 相交于点E 。

求证：直线AB 是线段CD 的垂直平分线。

AC DEBA B C NM AB C N M AB CN M例4：如图所示，在△ABC中，AB=AC，∠BAC=1200，D、F分别为AB、AC的中点，，，E、G在BC上，BC=15cm，求EG的长度。

⊥⊥DE AB FG ACAB E G C例5:：如图所示，Rt△ABC中，，D是AB上一点，BD=BC，过D作AB的垂线交AC于点E，CD交BE于点F。

求证：BE垂直平分CD。

CEFA D B例6:：在⊿ABC中，点O是AC边上一动点，过点O作直线M N∥BC，与F，求证：OE=OF例7、如图所示，AB>AC，∠A的平分线与BC的垂直平分线相交于D，自D作DE AB⊥于，求证：BE=CF。

E，DF AC FAEB M CFD答案如下：例1：解：（1）∵∠B= 1/2（180°-∠A）=70°，∴∠M=20°；（2）同理得，∠M=35°；（3）规律是：∠M的大小为∠A大小的一半，即：AB的垂直平分线与底边BC 所夹的锐角等于∠A的一半．证明：设∠A=α，则有∠B= 1/2（180°-α），∠M=90°- 1/2（180°-α）= 1/2α．（4）改为钝角后规律成立．上述规律为：等腰三角形一腰的垂直平分线与底边相交所成的锐角等于顶角的一半．例2：解：连接BF，由线段的垂直平分线的性质可得，FB＝FA又因为AC＝AF+CF ＝6，所以BF+CF＝6△BCF的周长＝BC+CF+BF＝4+6＝10例3：证明：因为AC=AD所以A在线段CD的垂直平分线上又因为BC=BD所以B在线段CD的垂直平分线上所以直线AB是线段CD的垂直平分线例4：解：作AH⊥BC于H，HC=15/2∵等腰∴∠ACB=∠ABC=30°∴AC=2EC/根号3EC=5根号3∵F为AC中点∴FC=5/2根号3∵FG⊥AC∴CG=5同理，BE=5∴EG=5例5：证明：∵DE⊥AB，∠ACB＝90∴∠BDE＝∠ACB＝90∵BD＝BC，BE＝BE∴△BCE≌△BDE （HL）∴∠CBE＝∠DBE∵BF＝BF∴△BCF≌△BDF （SAS）∴∠BFC＝∠BFD，CF＝DF∵∠BFC+∠BFD＝180∴∠BFC＝∠BFD＝90∴BE⊥CD∴BE垂直平分CD例6：解：∵MN∥BC，∴∠OEC=∠BCE，∠OFC=∠GCF，又已知CE平分∠BCO，CF平分∠GCO，∴∠OCE=∠BCE，∠OCF═∠GCF，∴∠OCE=∠OEC，∠OCF=∠OFC，∴EO=CO，FO=CO，∴EO=FO．例7：证明：连接DC，DB∵点D在BC的垂直平分线上∴DB=DC∵D在∠BAC的平分线上∴DE=DF∵∠DFC=∠DEB∴△DCF≌△DEB∴CF=BE最新文件仅供参考已改成word文本。

线段的垂直平分线、角平分线经典习题及答案由于A、B都在CD的垂直平分线上，所以直线AB是CD的垂直平分线。

证毕。

例4：解：连接EF，由于AB=AC，所以∠BAC=60°，∴∠DEG=30°，∠GFC=60°，又因为DE⊥AB，FG⊥AC，所以DEGF是一个菱形，且DG=GF=7.5cm，所以EG=2DGsin30°=7.5cm。

例5：证明：因为BD=BC，所以∠XXX∠CBD，又因为BE⊥CD，CF⊥BD，所以∠BEC=∠BCF，所以BE平分∠XXX，CF平分∠CBD，又因为∠XXX∠CBD，所以BE和CF都平分∠BCD，即BE垂直平分CD。

证毕。

例6：证明：连接OF，OE，MN，∵MN∥BC，∴∠EOF=∠ACB，又∠XXX∠EOM+∠MOF，∠XXX∠EOM+∠EOF，∴∠MOF=∠ACB-∠EOF，又因为EF是AC的角平分线，∴∠XXX∠EAF，又因为EF是AC的外角平分线，∴∠XXX∠XXX，∴∠MOF=∠ACB-∠XXX，又因为OE⊥AC，OF⊥AC，所以OE=OF，证毕。

例7：证明：连接AD，因为AD是∠A的平分线，所以∠EAD=∠FAD，又因为BD=BC，所以∠XXX∠DCB，又因为AD⊥DE，所以∠EDB=90°-∠XXX，又因为DF⊥CF，所以∠XXX°-∠DCB，所以∠EDB=∠XXX，又因为∠EAD=∠FAD，所以三角形ADE与三角形ADF全等，所以DE=DF，又因为BE⊥DE，CF⊥DF，所以BE=DEsin∠EDB=DFsin∠FDC=CF，证毕。

例4：根据题意，作AH垂直BC于点H，可以得到HC 的长度为15/2.由于△ABC是等腰三角形，所以∠ACB=∠ABC=30°。

根据正弦定理，可以求得AC的长度为5√3.由于F是AC的中点，所以FC的长度为5/2√3.根据勾股定理，可以得到CG和BE的长度都为5.因此，EG的长度也为5.例5：由于DE垂直于AB，而∠ACB=90°，所以∠BDE=∠ACB=90°。

线段的垂直平分线与角平分线【知识框架】1、线段垂直平分线的性质（1）垂直平分线性质定理：线段垂直平分线上的点到这条线段两个端点的距离相等.定理的数学表示：如图1，∵ CD ⊥AB ，且AD ＝BD∴ AC ＝BC.定理的作用：证明两条线段相等 （2）线段关于它的垂直平分线对称. 2、线段垂直平分线的判定定理：到一条线段两个端点距离相等的点在这条线段的垂直平分线上. 定理的数学表示：如图2，∵ AC ＝BC∴ 点C 在线段AB 的垂直平分线m 上.定理的作用：证明一个点在某线段的垂直平分线上. 3、关于线段垂直平分线性质定理的推论（1）关于三角形三边垂直平分线的性质：三角形三边的垂直平分线相交于一点，并且这一点到三个顶点．．．．．的距离相等.性质的作用：证明三角形内的线段相等.（2）三角形三边垂直平分线的交点位置与三角形形状的关系：若三角形是锐角三角形，则它三边垂直平分线的交点在三角形内部； 若三角形是直角三角形，则它三边垂直平分线的交点是其斜边的中点；若三角形是钝角三角形，则它三边垂直平分线的交点在三角形外部. 反之，也成立。

4、角平分线的性质定理：角平分线的性质定理：角平分线上的点到这个角的两边的距离相等.定理的数学表示：如图4，∵ OE 是∠AOB 的平分线，F 是OE 上一点，且CF ⊥OA 于点C ，DF ⊥OB于点D ， ∴ CF ＝DF.定理的作用：①证明两条线段相等；②用于几何作图问题； 角是一个轴对称图形，它的对称轴是角平分线所在的直线. 5、角平分线性质定理的逆定理：角平分线的判定定理：在角的内部到角的两边距离相等的点在这个角的角平分线上. 定理的数学表示：如图5，图1图2图4∵点P在∠AOB的内部，且PC⊥OA于C，PD⊥OB于D，且PC＝PD，∴点P在∠AOB的平分线上.定理的作用：用于证明两个角相等或证明一条射线是一个角的角平分线注意角平分线的性质定理与判定定理的区别和联系.（1）关于三角形三条角平分线交点的定理：三角形三条角平分线相交于一点，并且这一点到三边的距离相等.定理的数学表示：如图6，如果AP、BQ、CR分别是△ABC的内角∠BAC、∠ABC、∠ACB的平分线，那么：① AP、BQ、CR相交于一点I；②若ID、IE、IF分别垂直于BC、CA、AB于点D、E、F，则DI＝EI＝FI.定理的作用：①用于证明三角形内的线段相等；②用于实际中的几何作图问题.（2）三角形三条角平分线的交点位置与三角形形状的关系：三角形三个内角角平分线的交点一定在三角形的内部.这个交点叫做三角形的内心（即内切圆的圆心）.7、关于线段的垂直平分线和角平分线的作图：（1）会作已知线段的垂直平分线；（2）会作已知角的角平分线；（3）会作与线段垂直平分线和角平分线有关的简单综合问题的图形.【典型例题】例1、如图1，在△ABC 中，BC ＝8cm ，AB 的垂直平分线交AB 于点D ，交边AC 于点E ，△BCE 的周长等于18cm ，则AC 的长等于（ ） A ．6cm B ．8cm C ．10cm D ．12cm【跟踪练习】（1）如图，AB=AC=14cm,AB 的垂直平分线交AB 于点D ，交AC 于点E ， 如果△EBC 的周长是24cm ，那么BC=_________;（2）如图，AB=AC=14cm,AB 的垂直平分线交AB 于点D ，交AC 于点E ， 如果BC=8cm ，那么△EBC 的周长是______;（3）如图，AB=AC,AB 的垂直平分线交AB 于点D ，交AC 于点E ， 如果∠A=28度，那么∠EBC=___.例2、已知： AB=AC ，DB=DC ，E 是AD 上一点，求证：BE=CE.【跟踪练习】已知：在△ABC 中，ON 是AB 的垂直平分线,OA=OC.求证：点O 在BC 的垂直平分线.例3、在△ABC 中，AB=AC ，AB 的垂直平分线与边AC 所在的直线相交所成锐角为50°，△ABC 的底角C∠B的大小为_______________。