当前位置：文档之家 › 控制系统的频率特性(课堂PPT)

控制系统的频率特性(课堂PPT)

  • 格式：ppt
  • 大小：1.33 MB
  • 文档页数：16

下载文档原格式

  / 16

合集下载

控制系统频率分析课件

控制系统频率分析课件

仍能保持稳定运行。
分析系统动态性能
频率分析可以揭示控制系统的动 态性能，包括系统的响应速度、 阻尼比和超调量等，为系统性能
优化提供依据。
指导控制器设计
通过频率分析方法，可以根据系 统性能要求，指导控制器参数和 结构的设计，实现控制系统的优
化。
课件内容与结构
1 2 3
基础知识介绍 课件首先对控制系统频率分析的基础知识进行介 绍，包括频率特性的概念、分类和作用等，为后 续内容打下基础。
动执行器等。
03
控制器
介绍控制器的结构、原理和分类，包括模拟控制器、数字控制器等，并
详细阐述PID控制算法的实现方法和优缺点。
控制系统性能指标
稳定性
阐述稳定性的概念、判定方法和改善措施，包括劳斯判据、奈奎 斯特判据等。
动态性能
介绍动态性能指标的定义和计算方法，包括上升时间、调节时间、 超调量等，并分析各指标对系统性能的影响。
根据系统特点选择合适的坐标系，便于观察和分析。
确定关键点
确定系统的关键频率点，如截止频率、穿越频率 等，便于分析和设计。
利用渐近线
利用渐近线绘制开环频率特性曲线，便于快速分 析和估算。
开环稳定性判定方法
Nyquist稳定判据
根据Nyquist稳定判据判断系统的稳定性，包括判断曲线是否包围临界点、计算相角裕度和幅值裕度等。
稳定性判定依据
01
02
03
稳定性概念
系统在受到扰动后，能否 恢复到平衡状态的能力。 稳定性是控制系统正常工 作的前提。
稳定性判定方法
劳斯判据、奈奎斯特判据、 伯德图判据等。通过对系 统传递函数的分析，判断 系统是否稳定。
稳定性判定实例
针对具体控制系统，运用 稳定性判定方法进行实例 分析，加深对稳定性概念 的理解。
第四章 控制系统的频率特性PPT课件

第四章 控制系统的频率特性PPT课件

一·乃氏图的一般作图法
1·写出 G ( j w ) 和G( jw)表达式； 2·分别求出 w 0 和 w时的 G ( j w ) ；
3·求乃氏图与实轴的交点，交点可利用 ImG(jw)0或 G(jw)n180o
的关系式求出；
4·求乃氏图与虚轴的交点，交点可利用 ReG(jw)0或 G(jw)n90o
K;
(T 1s1 )(T 2s1 )
K ,T 1,T 20
试概略绘制系统开环幅相曲线。
解：由于惯性环节的角度变化为 ～-900，故该系统开环幅
相曲线中
起点为：
终点为：
系统开环频率特性
A (0)K,
(0)00
A ( ) 0 , ( )2 ( 90) 0 10 80
G (j)K [1 (1 T 1 T T 12 2 2 2) 1 (j (T T 1 22 T 22 ))]
即多环节传递函数的幅频特性是各环节模的乘积，相频特性是各环节 相位角之和。
7
自动控制原理
§4-2频率响应的极 频率响应G(jw)是输入频率w的复变函数，是一种变换，当w从0逐渐增长至
时，G(jw)作为一个矢量，其端点在复平面相对应的轨迹就是频率响
应的极坐标图，亦叫坐做乃标氏图图（（Nyq乃uist氏曲线图） ）
传递函数G(s)
S=jw
频率特性G(jw)
注：系统频率特性分析法是一种用“稳态”的方法（即输出稳态时 的正弦信号，不考虑过度过程）来分析系统的动态特性（稳，准， 快）
5
自动控制原理
二·频率特性的一些概念
G (jw ) U (w )jV (w )
幅频特性 A (w ) G (jw )[U (w )]2 [V (w )]2
(jw K)(j(wjw1T11)1()j(wjw2T21).1..)...
自动控制原理 频率特性图文PPT课件

自动控制原理 频率特性图文PPT课件


惯性环节的奈氏图
(1) 奈氏图
Im
传递函数和频率特性 绘取制特奈殊氏点图：近似方法:
ω ∞0
ω=0
ωω φφ ω=
=01 T
=∞
幅根频据G特幅A(sA((性频A)ωω(=ω((和特))ωω==)-=0))相性4==.07501T频和0oso7+特相11性频特性求出特G殊(jω点),=然后-将45它jω们T+1平ω1滑= 连1T接起来.
第23页/共106页
第二节 典型环节的频率特性
从图可知,当ζ较小时，对数幅频特性曲线出现了峰值，称为谐振峰值 Mr，对应的频率称为谐振频率ωr。
精确曲线与渐近线之间存在的误差与ζ值有关，ζ过大或过小，误差都 较大，曲线应作出修正。
dA(ω) =0
dω
可求得
(0≤ζ≤0.707)
代入得
Mr=A(ωr)=
Im
ω∞
0
Re
ω ω= 0
第8页/共106页
第一节 频率特性的基本概 念
2．对数频率特性曲线
L性也纵Φ特坐分性德特数线频称记((单是坐曲ωω性标度纵曲图性相组率为作由)位对标l)线=对g曲采。坐对线曲频成变.十 d。对2为数ω则的e数0线用标数又 线 。 化特倍c数l频表横分dg相的.为幅称 和 十性频幅lAB率g示坐度频横频(伯 对 倍曲程ω频ω特为标，特，，) -1---29842400000000
一、典型环节的频率特性 二、控制系统开环频率特性
第10页/共106页
第二节 典型环节的频率特性
1．比例环节
传递函数和频率特性
G(s)=K
G(jω)=K
幅频特性和相频特性
A(ω)=K
φ(ω)=0o
自动控制原理与系统__课件第四章控制系统的频率特性

自动控制原理与系统__课件第四章控制系统的频率特性


由拉氏变换可知，传递函数的复变量s =σ+jω。 当σ=0时，s = jω。所以G（jω）就是σ=0时 的G（s），即复域与频域的关系为：
传递函数 G(s) 频率特性 s j G(jω )
s j
5
三、频率特性的表示方法
1、数学式表示法
G (j ) G (j ) G (j )
arctanT
对数幅频特性L(ω)是一条曲线,逐点描绘很烦琐,通常采用近似 的绘制方法,用两条渐进线近似表示.
低频渐近线： 高频渐近线：
T 1 L 20 lg 1 0
3
低频渐近线为零分贝线。
高频渐近线为一条在ω=1/T处穿越横轴、且斜率为-20dB/dec的直线。对 数幅频特性曲线可近似地用上述两条直线表示，且它们相交于ω=1/T（转 折频率）处。由这两条直线构成的近似对数幅频特性曲线称为 渐近对
对数相频特性φ(ω) 低 频 ： 当 ω→0 时 ， φ(ω)→0。因此，低频段为 一条φ(ω)→0的水平线。 高频：当ω→∞时，φ(ω) →-180o 。因此，高频段一条 φ(ω)→-180o的水平线。 交接频率处的相位：当 ω=ωn时，φ(ω)=-90o。
20
振荡环节的对数相频特性既 是ω的函数，又是ζ的函数。 随阻尼比ζ不同，对数相频特 性在转折频率附近的变化速 度也不同。ζ越小，相频特性 在转折频率附近的变化速度 越大，而在远离转折频率处 的变化速度越小。
（极坐标表示法）
U ( ) jV ( )
（直角坐标表示法）
（指数表示法） A ( )e j ( )
V ( ) U ( )
图4-2
A ( ) G (j ) U 2 ( ) V 2 ( )
系统的频率特性(课堂PPT)

系统的频率特性(课堂PPT)


过点（1 ，0），斜率为20db / dec直线 T
可以看出一阶微分环节和 惯性环节的对数幅频图对 称于零分贝线。
28
1
（6）振荡环节 1 2 j （ j）2
n n
幅频特性
L()= 20lg 1 2
1
j ( j )2
= - 20 lg
（1-
2 n2
）2 +
（2
）2 dB n
n n
（5－25）
相频特性
7
3. 机械系统动刚度的概念
图3-2所示，质量－弹簧－阻尼系 统，传递函数为：
G(s)=
X (s) = F (s)
1 ms2+ Bs+ k
=
1 k
s2
n2
1
+ 2 n
s+1
系统阻尼比＝ ，B 系统无阻尼自然频率
2 mk
系统的频率特性为：
G( j)=
X ( j) = F ( j)
1 k
(1-
1
2 n2
)+
j
2 n
。n＝
k m
8
上式反映了动态作用力 （f t与）系统动态变形 之（x t间）的关 系，实质上 G（表j示）的是机械结构的动柔度 ，（也j就）是 它的动刚度 的倒K（数j。）
当＝0时
G（j）＝（j）＝
1
K（j）
K（j）＝0
＝1
G（j）＝0
＝k
（ 1－
2 n2
）＋j
2 n
＝0
＝k
即该机械系统的静刚度为k。
（5－8）
式中：
C( j)= L c(t) = c(t)e- stdt c(t)e- jtdt
控制系统频率分析PPT课件

控制系统频率分析PPT课件


10K0
1 0.1
1 10
20lg
10K0 3
10
﹣40dB/dec
0.1 c 10
c
0.167 属于
0.1 10
的频率范围，
所以有
20
lg
K0 0.1672
0
K0 0.0279
第9页/共14页
例2：
第五章频率特性分析 §4 控制系统稳定裕度及系统带宽
解：
(4) 系统有一延滞环节 e s 时， 在什么范围内系统是稳定。
以－60dB/dec斜率穿越0dB 线，系统不稳定。
第3页/共14页
一、稳定裕度(适用最小相位系统)
第五章频率特性分析 §4 控制系统稳定裕度及系统带宽
例 1 ：图中所示为 一个宇宙 飞船控制 系统的方 块图 。为 了使
相位裕度等于50°，试确定增益K值，此时，幅值裕度是多少？
1
﹣ K(s+2)
S2
K( j 2)
( j)2
1
2.38
2.38
K
1.8
22 2.382
这个K值将产生相位裕度50°。
第5页/共14页
第五章频率特性分析 §4 控制系统稳定裕度及系统带宽
例2：已知最小相位（单位反馈）开环系统
的渐近对数幅频特性如图所示，试：
20lgG/dB
(1) 求取系统的开环传递函数。
40
(2) 用稳定裕度判断系统稳定性。
当 g c时，r=0，R’=0。系统稳定裕度为0，处于临界稳定
第1页/共14页
一、稳定裕度(适用最小相位系统)
第五章频率特性分析 §4 控制系统稳定裕度及系统带宽
对数坐标图上稳定裕度的表示法：
自动控制原理 第五章 频率特性) ppt课件

自动控制原理 第五章 频率特性) ppt课件

无法观察到这种稳态响应。从理论上讲，系统动态过程的稳态分 量（从全解的形式中理解）总可以分离出来。
系统微分方程的全解＝齐次通解+稳态特解 稳态特解就是稳态分量，即频率特性定义中要用到的量。
2019/11/12
PPT课件
19
19
（5）频率特性的求取
① 根据定义求取 对已知系统的微分方程，把正弦输入函数代入，求出其稳态
数给定了，则系统的频率特性也完全确定。
② 系统的稳态输出量与输入量具有相同的频率 当输入量频率改变，则输出、输入量的幅值之比A（）和
它们的相位移（）也随之改变。所以 A（）和（）都是 的函数。这是由于系统中的储能元件引起的。
2019/11/12
PPT课件
18
18
③ 频率特性是一种稳态响应，但表示的是系统动态特性 频率特性是在系统稳定的前提下求得的，对于不稳定系统则
b() d ()
2019/11/12
关于ω的奇PP次T课件幂多项式
13
13
G( j) arc tan( b ) arc tan( d )
a
c
G( j) arc tan( bc ad )
ac bd
tan(a b) tan a tan b 1 tan a tan b
uo
t t
8
8
RC网络的输入与输出的关系为：
T
duo dt
uo

ui
式中，T RC ，为时间常数。取拉氏变换并代入初始条件得
1
1 A
Uo (s)

Ts
1[Ui (s)
Tuo0
]
Ts[ 1s源自22 Tuo0
]
拉氏反变换得
第四章控制系统的频率特性分析课件

第四章控制系统的频率特性分析课件

4-0 引言
频率响应法是二十世纪三十年代发展起来的一种经典工 程实用方法,是一种利用频率特性进行控制系统分析的图解方 法,可方便地用于控制工程中的系统分析与设计。频率法用于 分析和设计系统有如下优点：
（1）不必求解系统的特征根，采用较为简单的图解方法 就可研究系统的稳定性。由于频率响应法主要通过开环频率特 性的图形对系统进行分析，因而具有形象直观和计算量少的特 点。
❖数学本质
输入 xi(t) Xi sin(t)
输出
xo(t ) ae jt ae jt G( jw) e j ( )e jt Xi G( jw) e e j ( ) jt Xi
2j
2j
G( jw) Xi sin(t ( ))
Xo() sin(t ())
式中：Xo(ω) 为输出正弦信号的幅值，Φ(ω)为输出正弦
当在0～变化时,向量G( j)H(j)的幅值和相角随而变化,与此对应 的向量G( j)H(j)的端点在复平面G( j)H(j)上的运动轨迹就称为幅相 频率特性或 Nyqusit曲线。画有Nyqusit曲线的坐标图称为极坐标图或 Nyqusit图。
4-1 频率特性的基本概念
2.伯德图(Bode图) 如将系统频率特性G( j)的幅值和相角分别绘在半对数坐标
4-0 引言
（2）系统的频率特性可用实验方法测出。频率特性具 有明确的物理意义，它可以用实验的方法来确定，这对于难 以列写微分方程式的元部件或系统来说，具有重要的实际意 义。
（3）可推广应用于某些非线性系统。频率响应法不仅适 用于线性定常系统，而且还适用于传递函数中含有延迟环节 的系统和部分非线性系统的分析。
所以，
G(
j
)
Xo( )
A( )
Hale Waihona Puke XiG( j) ()
控制系统的开环频率特性 ppt课件

控制系统的开环频率特性 ppt课件


1
wKN
这一点）。
L(w) dB 20lgK
L(w) dB
-20dB/dec 20lgK
L(w) dB -40dB/dec
20lgK
0型系统 w
Kw
1 I型系统
Kw
1 II型系统17
2、完成低频段渐近线后，再继续绘制中、高频段渐 近线
以 G(jw) K 为例（设K>1, T>1）
jw(jTw1)
①先画低频段渐近线 ②再画出惯性环节的渐近线 ③将曲线①和②叠加
控制系统的开环频率特性
1
5-3 控制系统的开环频率特性
典型环节 频率特性
(7种)
幅 相 曲 线
开环系统 频率特性
幅 相 曲 线
2
精品资料
你怎么称呼老师？ 如果老师最后没有总结一节课的重点的难点，你 是否会认为老师的教学方法需要改进？ 你所经历的课堂，是讲座式还是讨论式？ 教师的教鞭 “不怕太阳晒，也不怕那风雨狂，只怕先生骂我 笨，没有学问无颜见爹娘 ……” “太阳当空照，花儿对我笑，小鸟说早早早……”
修正值： 0 . 2 ,w n 1 ,w r 0 9 . 5 ,L m 9 8 . 1 d 4
5 10
w
100
-93.7 -40
-137.5
23
例：已知系统的开环传递函数为
G(s) 10(S2) (S1)(S10)
要求绘制Bode图。
2( 1 s 1)
G(s)
(s
2 1)(
1
s 1)
(w) 。
对于最小相位系统，当w→∞时， (w) →－(n-m) ×90°
20
L w 已知开环传递函数
40db 20db
控制工程第四版第4讲_频率特性_02.pptx

控制工程第四版第4讲_频率特性_02.pptx


第四章 控制系统的频率特性
Y 则 X X Y 0 N 配方整理，可得
2 2
1 1 1 1 X Y 2 2 N 4 2 N
2
2
2
由上式可看出，等相角轨迹是一个圆心
1 1 为 , j ，半径为 2 2N
闭环截止频率 b： 对数幅频特性的幅值下 降到-3dB时对应的频率。
第四章 控制系统的频率特性 4.8 机械系统动刚度概念 一个典型的由质量-弹簧-阻尼构成的机械系 统的质量块在输入力f(t) 作用下产生的输出位移 为y(t)，其传递函数为
Y s 1 1k G s 2 2 2 F s ms Ds k s n 2 s n 1
2 2
Im G j arc tan Re
第四章 控制系统的频率特性 4.5节小结 频率特性函数的求取方法：
1.根据系统的传递函数求取
2.根据系统的微分方程求取 3.实验方法：
输入不同频率的正弦信号
输入脉冲信号
第四章 控制系统的频率特性 4.6 对数幅相特性图（Nichols 图）
第四章 控制系统的频率特性
在由开环频率特性确定闭环频率特性时，应 用相同的比例尺，将尼柯尔斯图线绘制在透明 片上，然后再把它覆盖在以相同比例尺绘制的 系统开环传递函数对数幅相图上，则开环频率 特性曲线G( j ) 与M轨线和N 轨线的交点，就给出 了每一频率上闭环频率特性的幅值M 和相角φ。
若 G( j ) 轨迹与M轨线相切，切点 处频率就是谐振频率，谐振峰值由M轨 线对应的幅值确定。
系统单位脉冲响应的傅氏变换即为 系统的频率特性。
第四章 控制系统的频率特性
为了识别系统的传递函数，我们可以产生一 个近似的单位脉冲信号 (t ) 作为系统的输入，记 录系统响应的曲线 g (t ) ,则系统的频率特性为
69自动控制原理1第一节频率特性的基本概念PPT课件

69自动控制原理1第一节频率特性的基本概念PPT课件


9/18/2020
4
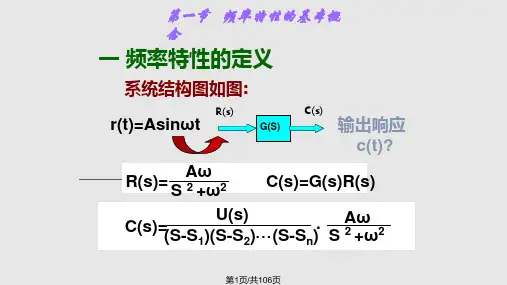
一、频率特性的定义： 系统的频率响应定义为系统在正弦作用下稳态响应的振幅、
相位与所加正弦作用的频率之间的依赖关系。
对于一般的线性定常系统，系统的输入和输出分别为r(t)和 c(t)，系统的传递函数为G(s)。
G (s)C (s)
N (s)
R (s) (sp 1)s(p 2).s. .p (n)
R( j) Rmejx ,C( j) Cmejy C(j) Cm ej(yx) A()ej() R(j) Rm
可见，频率特性就是输出、输入正弦函数用矢量表示时之比。
表示线性系统在稳态情况下，输出、输入正弦信号之间的数学 关系。是频率域中的数学模型。
9/18/020
11
[例子]：设传递函数为：G(s)xy((ss))s231s4 微分方程为：x y((tt))d d2 2t3 1d d t4, d2 d y2 (tt)3dd (ty )t4y(t)x(t)
频率响应法的优点之二在于它可以用图来表示，这在控制 系统的分析和设计中有非常重要的作用。
9/18/2020
13
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
为频率特性。反之亦然。
到目前为止，我们已学习过的线性系统的数学模型有以下
几种：微分方程、传递函数、脉冲响应函数和频率特性。它们
之间的关系如下： 微分方程
j d
dt
频率特性
s d dt
传递函数
s j
L{g(t)} L1{G(s)}
脉冲函数
9/18/2020

第五章控制系统的频率特性分析法精品PPT课件


二阶超前、滞后系统
G(S)
2 0
S
2
2
0S
2 0
G( j )
2 0
1
2
2
j
0
2 0
1 2 j ( )2
0 0
2
1
jtg
1
1 (
0
)2
e
0
[1 ( ) 2 ]2 (2 ) 2
0
0
20 lg G ( j ) 20 lg
1
[1 ( ) 2 ]2 (2 ) 2
0
0
2
( ) tg 1
aG(S)•R(S)(Sj)Sj
G(j)
jAjA•G 2(jj)
G( j) G( j) ej G( j) G( j) e j
y(t) AG( j) e j e jt AG( j) e j ejt
2j
2j
AG( j) [e j(t) e j(t) ]
2j
AG( j) •sin(t ) B•in(t )1lgω
20lg|G（jω）|
频率特性 G（jω）=K/（jω）r=K/ωr e-j90r
20lg|G（jω）|=20（lgK-rlgω） ；φ（ω）=-900 r
一阶超前、滞后系统
滞后环节： G(S) 1 TS1
G(j)
1
ejtg1T
Tj 1 T22 1
2l0g G (j)10 lgT2 (21)
()tg 1T
渐近线： Tω＜＜1时，
2l0 G g (j) 1l0 1 g 0
Tω＞＞1时
2l0 G g (j) 1l0 T g 22 2lT 0 g
转折频率： 20lgTω=0 ω=1/T

自动控制原理--频率特性及其表示法 ppt课件


由复阻抗的概念求得
图5.3 RC串联电路
Uo ( j) G( j) 1 1
Ui ( j)
1 RCj 1 jT
式中: T RC
自动控制原理
ppt课件
9
1 频率特性的基本概念
RC电路的频率特性 G( j) G( j) e j()
由该电路的结构和参数决定，与输入信号的幅
幅值衰减。
频率特性可应用到某些非线性系统的分析中去
自动控制原理
ppt课件
13
1 频率特性的基本概念
频率特性的求取
根据定义求取 对已知系统的微分方程，把正弦输入函数代
入，求出其稳态解，取输出稳态分量与输入正弦 量的复数比即可得到。
根据传递函数求取 用s=j代入系统的传递函数即可得到。
通过实验的方法直接测得
幅相频率特性
幅相频率特性的图示 也称为奈奎斯特曲线（奈氏图）或极坐标图。
极点
坐标轴
(i )
A(i )
(a)
jI() R(i)
jI ( )
I (i )
(i) R()
A(i )
(2)
A(2 )

(1) A(1)
R()
G( j1)
G( j2)
(b)
(c)
图5.4 幅相频率特性表示法
系统频率特性能间接地揭示系统的动态特性和 稳态特性，可简单迅速地判断某些环节或参数对系 统性能的影响，指出系统改进方向。
频率特性可以由实验确定，这对于难以建立动 态模型的系统来说，很有用处。
自动控制原理
ppt课件
2
5.1 频率特性及其表示法
1 频率特性的基本概念 2 频率特性的表示
自动控制原理
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2
频域法是利用频率特性研究自动控制系统的一种古典方 法，它有如下特点
1) 应用Nyquist(奈奎斯特)稳定性判据，可以根据系统的开环频率特 性，研究闭环系统的稳定性，而不必求特征方程的根。
2) 对于二阶系统，频率响应和瞬态响应的性能指标之间有确定的对 应关系，而高阶系统也存在类似的关系。因为系统的频率特性与系 统参数、结构之间有着密切关系，所以可以利用研究频率特性的方 法，把系统的参数、结构变化和瞬态响应性能指标之间联系起来。
2 写出开环系统的A(ω)和φ(ω)表达式。
3 分别求出ω=0和ω为无穷时的G(j ω)。 4 求Nyquist与实轴交点，交点可用Im[G(j ω)]=0求出。 5 求Nyquist与虚轴交点，交点可用Re[G(j ω)]=0求出。 6 必要时再画出中间几点。 7 勾画大致曲线，
21
4.3 频率响应的Bode图(对数坐标图)
第4章 控制系统的频率特性
4.1 频率特性 4.2 频率响应的Nyquist 图 4.3 频率响应的Bode图 4.4 控制系统的闭环频率响应
1
时域分析法研究系统的各种动态与稳态性 能比较直观、准确
缺点是： 1. 当某些系统工作机理不明了时，数学模型难以确定， 因而无法分析系统性能。
2. 当系统的响应不能满足技术要求时，也不容易确 定应该如何调整系统来获得预期效果。
A G j U 2 V 2 s
V A sin
9
二. 频率特性的几何表示
1. 幅相频率特性（Nyquist 图）
当频率 从0到无穷大变化 时，向量G(j )的端点在复
平面上的运动轨迹。 规定极坐标图的实轴正方向为相角零度线，逆时针转过
1 2T 2
5
定义：
A() A / 1 2T 2
A
1
1 2T 2
稳态输出幅值 输入幅值
RC网络幅 频特性
() arctanT 稳态输出相位 输入相位 RC网络相频特性
1
1 2T 2
arctan T
6
将s以j 代入RC网络传递函数，即得RC网络频率特性
G( j) 1 1 RCj 1 1 jT
3
4.1 频率特性
一.频率特性的基本概念
xi(t)
R
xi(t) t
xo(t) C
RC网络的传递函数为
G(s)
X 0 s Xi s
1 Ts 1
4
输入信号 xi t Asin t
输出信号
x0
t
1
AT 2T
2
t
eT
A sint arctanT
1 2T 2
系统稳态输出
lim
t
x0
t
A sin t arctan T
G j
X 0 j X i j
8
频率特性的矢量图
jv
频率特性是一个复数，有三种表示：
V ()
A() ()
G(j) 代数式 G j U jV
极坐标式
0
U() u G( j) G( j) G( j) A() ()
指数式
G( j ) G( j ) e jG( j ) A( )e j ( )
的角度为正，顺时针转过的角度为负。
2. 对数频率特性（Bode图） 由两张图组成：一张是对数幅频特性，另一张是对数相频 特性。
10
RC网络的幅相曲线绘在s平面上
jv
0 →∞ -45°
0.707
=0 u
=1/T
11
4.2 频率响应的Nyquist 图
一. 典型环节的Nyquist图
1. 放大环节
频率特性 G j K
jv
幅频特性 A G j K
0
相频特性 G j 0o
K u
12
2. 积分环节
频率特性
G j
1
1
j( )
e2
j
幅频特性 A G j 1
相频特性 G j 90
jv
0
u →∞
=0
13
3. 微分环节
频率特性
G j
j
j
e 2
幅频特性 A G j
相频特性 G j 90
3) 频率特性有明确的物理意义，很多元件的这一特性都可以用实验 的方法确定，这对难于分析其物理规律来列出微分方程的元部件和 系统，有很重要的工程实际意义。
4) 频率特性分析法不仅适用于线性系统，而且可以推广到某些非线 性系统。
5) 当系统在某些频率范围存在着严重噪声时，应用频率法，可以设 计出能够很好抑制这些噪声的系统。
∞
jv
↑
2
45° =0
0
1
u
实频特性 U ( ) 1
16
6. 二阶振荡环节
频率特性
G j
1
j 2T 2 j2T 1
幅频特性 A G j
1
1 2T 2 2 2T 2
相频A特性GGjjG1ajrct2aTn21122arc22TTtaa2nrcT1ta22n1T122TT22TT2
A( 1
e j(arctanT )
1 2T 2
)e j ( )
RC电路的这一特性，对于任何稳定的线性网络都成立
虽然在前面的分析中，设定输入信号是正弦信号，然而频 率特性是系统的固有特性，与输入信号无关， 即当输入为非正弦信号时，系统仍然具有自身的频率特性。
7
频率特性定义为输出量的Fourier变换与输入量 的Fourier变换之比，即
r n 1 2 2 0.707
M r A max
2
1
1 2
2 2
18
7. 二阶微分环节
jv
=0
01
u
19
8. 延迟环节
频率特性 G j e jT
幅频特性 A 1
A 1 相频特性 T
jv
1 0
=0
u
20
二.Nyquist图的一般作图方法
1 分别写出开环系统中各个典型环节的幅频特性和相 频特性。
jv
∞
↑
=0
0
u
14
4.一阶惯性环节
频率特性 G j 1
1 jT
幅频特性 A 1
2T 2 1
jv
0 →∞ -45°
0.707
1 =0 u
相频特性 arctanT
=1/T
一阶惯性环节的幅相频率特性曲 线是一个半圆。
15
5. 一阶微分环节
频率特性 G j Tj 1
幅频特性 A 1 T 2 相频特性 arctan T
1 T
1 T
arctan
2T 1 2T
2
1 T
17
jv
振荡环节的 Nyquist曲线不
→∞
0
1
=0
n =1
仅与频率 有关，而且与
阻尼比ξ也有关。 ξ 越小， u 幅频越大。
n =0.5
n =0.3
当ξ 小到一定程度时，幅 频将会出现峰值：
M r A(r )
r为谐振频率
Mr为谐振峰值