小学一年级奥数课件：《变与不变》

4 变与不变学习目标:1、能通过生活实践及生活经验解决变与不变问题，掌握仔细观察、分析、比较的能力。

2、感受数学来源于生活，激发学生学习数学的兴趣。

教学重点:通过观察水位高低、糖块多少，判断甜度。

教学难点：培养简单归纳总结的能力。

教具准备:杯子、水、大小两块铁块、两种颜色记号笔教学过程：一、情景体验展示PPT师：一只乌鸦口渴了，到处找水喝。

乌鸦看见一个瓶子，瓶子里有水。

可是瓶子里水不多，瓶口又小，乌鸦喝不着水，怎么办呢？乌鸦看见旁边有许多小石子，想出办法来了。

乌鸦把小石子一个一个地放进瓶子里。

瓶子里的水渐渐升高，乌鸦就喝着水了。

这个过程中瓶子里的水变多了吗？（学生讨论）师：这个过程中虽然瓶子里的水渐渐升高，但是瓶子里的水并没有变多。

我们今天就一起来探讨变与不变的问题！（板书课题）二、例题讲解展示例1杯子外面有两个铁块，一块大的，一块小的。

大的铁块放进杯子里与小的铁块放进杯子里，水位的变化有什么不同？师：老师来给大家演示，大家注意观察。

现在老师的玻璃杯里装了半杯的水，我先把一块大铁块放进杯子里，大家看看水位有什么变化？生：水位升高了。

师：观察真仔细，我们给现在的水位用红色的记号笔做个标记。

师：现在老师把大铁块拿出来，再把一块小铁块放进杯子里，大家再看看水位有什么变化？生：水位也升高了。

师：我们给这时的水位用紫色的记号笔做个标记，比较下红色和紫色的水位哪个更高？生：红色的更高。

师总结：说明了放入大铁快水位比放入小铁块水位更高。

展示例2三个杯子一样大，里面装了水，在每个杯子里都放了一块石头，你知道哪个杯子里的石头最大？为什么？师：观察没有放入石头时三杯水的水位，你有什么发现？生：第一杯水最多，第二杯水最少。

师：再观察放入石头之后三杯水的水位，你有什么发现？生：三杯水水位一样高。

师：上下对比，哪个杯子放入石头之后水位升高的最多？生：第二杯水位升高的最多。

师：通过例1我们知道放入大铁快水位比放入小铁块水位更高，那么现在大家知道哪个杯子里的石头最大吗？生：第二个杯子里的石头最大。

奥数中的“变与不变”：对应数量亲爱的同学们，欢迎来到奥数的世界！在我们的生活中，有很多有趣的问题，今天我们就来一起探讨一下“变与不变”的问题吧！首先，让我们来做一个简单的实验。

假设我们有3个小朋友A、B、C，他们每个人都有3个糖果。

我们让他们每个人拿出1个糖果，那么他们三个人一共拿出了几个糖果呢？这是一个非常简单的问题，我们知道3个小朋友一共拿出3个糖果。

但是，如果我们让每个小朋友都拿出2个糖果呢？那么他们三个人一共会拿出几个糖果呢？聪明的你是不是已经发现了，他们一共拿出的糖果数是不变的，还是3个。

这就是我们生活中的“变与不变”的问题。

有时候，有些事物在变化的过程中，它们的总数是不变的。

比如我们每个人的年龄，我们在一年一年地增长，但是我们的年龄之和却是不变的。

那么，我们如何用数学的方式来描述这种“变与不变”的问题呢？其实，这正是我们奥数中的一个重要概念——对应数量。

在变化的过程中，如果我们想要保持总数不变，那么我们就需要找到一种对应数量，使得在变化的过程中，这种对应数量能够保持不变。

让我们来看一个具体的例子。

假设我们有5个小朋友A、B、C、D、E，他们每个人都想要拿出自己的一半糖果。

我们假设每个小朋友一开始有2个糖果，那么他们五个人一共拿出几个糖果呢？我们可以先计算每个小朋友的一半糖果数，然后再将它们相加。

假设每个小朋友的一半糖果数为a, b, c, d, e，那么我们可以得到以下等式：a +b +c +d +e = 5（每个小朋友的对应数量之和）如果我们想要保持总数不变，那么我们就需要找到一种对应数量，使得在这个变化的过程中，这种对应数量能够保持不变。

在这个例子中，我们可以看到每个小朋友的一半糖果数是不变的。

这是因为无论每个人拿出的糖果数是多少，他们的对应数量总是相等的。

所以，我们可以用对应数量来解决生活中的“变与不变”的问题。

这种方法不仅可以帮助我们更好地理解生活中的数学现象，还可以让我们更好地解决奥数中的难题。

变与不变
1．两个数相加，一个加数增加8，另一个加数也增加8，和有什么变化？、‘
2．两个数相加，一个加数增加9，另一个加数减少9．和起什么变化？
3．两个数相加，如果一个加数增加8，要使和增加14，那么，另一个加数应有什么变化？4．两个数相加，如果一个加数增加8，要使和减少4，那么另一个加数应有什么变化？
5．两个数相减，如果被减数不变，减数减少10，那么差会有怎样的变化？
6．两数相减，被减数减少18，如果要使差不变，减数应有怎样的变化？
7．两数相减，被减数增15，如果要使差增8 ;减数应有怎确5变化？
8．两数相减，如果减数增加30，要使差不变，被减数应有怎么变化？
9．两数相减．如果减数增加32，要使差减少29，被减数应有怎样的变化？
10．两数相乘，如果一个因数扩夫3倍，另一个因数缩小3倍，积将怎样？
11．两数相乘，一个因数缩小3悟，要使积不变，另一个因数应有什么变化？
12．两数相乘，如果一个因数缩小2倍，现在要使积扩大6倍，那么另一个因数应有什么变化？13．两数相除，如果被除数扩大4倍，除数扩大2倍，商将怎样变化？
14.两数相除，如果除数扩大5倍，要使商缩小5倍，被除数应怎样变化？
15.两数相除．商为21，如果除数缩小6倍，要使商缩小3倍，除数应怎样变化？
16.两数相除，如果除数扩大5倍，要使商缩小5倍，商是18,
多少？余数是多少？。

第二章比一比看一看第3讲变与不变【专题导引】小朋友，你知道吗？把一块石头放进瓶子里，瓶子里的水会有什么变化？对了，瓶子里的水位就会升高。

把放进去的石头再拿出来，水又会怎样变化呢？下面，我们就来找一找变与不变的规律。

在某一物体中再添加一些物体，总量就会增加，在某一物体中取走一些物体，总量就会减少。

而仅仅是把物体改变它的形状或大小，质量就不会改变。

【专题导引】【B1】杯子外面有两块石头，一块大的，一块小的。

大的石头放进杯子里与小的石头放进杯子里，水的变化有什么不同？解答：大石块放进杯子里，水面升高得多；小石块放进杯子里，水面升高得少。

【试一试】杯子外面有两块铁块，一块大的，一块小的，大铁块放进杯子里与小铁块放进杯子里，水的变化有什么不同？解答：大铁块放进杯子里，水面要比小铁块放进杯子里升高得多。

【B1】下面左边两只杯子一样大，里面盛的水也一样多。

如果把左边杯子里的水分别倒入右边的杯子里，右边的两个杯子里的水还是一样多吗？解答：水倒入另外一个容器中不变，右边两个杯子里的水一样多。

【试一试】有两块石头，一块大的，一块小的，分别放进了同样大小的杯子里，且杯子里装的水同样多。

请问哪杯是放进了大的石头，哪杯是放进了小的石头？解答：A杯中水面要比B杯中水面高，所以A杯放进了大石头，B杯放进了小石头。

【B3】分别在没有石头的上排的杯里放入石头后变成下排之图，哪个杯里的石头最大？解答：B杯中水面升高得最多，所以B杯里的石头最大。

【试一试】分别在上排没有石头的杯子里各放一块铁块后变CA BA B成下排的图，哪个杯子里面的铁块最小？解答：第（3）个杯子中水面升高得最少，所以第（3）个杯子里面的铁块最小。

【A1】两块一样的方糖，各放一块到杯子里，哪杯水甜？解答：B杯中水少一些，所以B杯中水更甜。

【试一试】在下面的4杯淡水中，每杯放进同样的2块方糖，哪一杯水最甜，为什么？解答：第（2）杯最甜，因为第（2）杯水最少。

【A2】三杯糖水一样甜，哪杯水里放进去的糖最少？解答：第（1）杯最少，因为第（1）杯中水最少。

变与不变
例1：两个数相加，一个加数减少6，另一个加数增加6，和是否起变化？
例2：两个加数相加，一个加数增加12，要使和增加3，那么另一个加数要有什么变化？
例3：两个数相减，如果被减数增加8，减数也增加8，差是否起变化？
例4：两数相减，如果被减数减少16，要使差减少18，减数应该起什么变化？
例5：两个数相乘，如果一个因数扩大4倍，另一个因数缩小2倍，积将有什么变化？
例6：两个数相乘，一个因数扩大2倍，要使积扩大6倍，另一个因数应该怎样变化？
例7：两个数相除，如果被除数扩大4倍，除数缩小3倍，商将怎样变化？
例8：两个数相乘，积是60，如果一个因数扩大2倍，另一个因素缩小3倍，那么两个数的积是多少？。

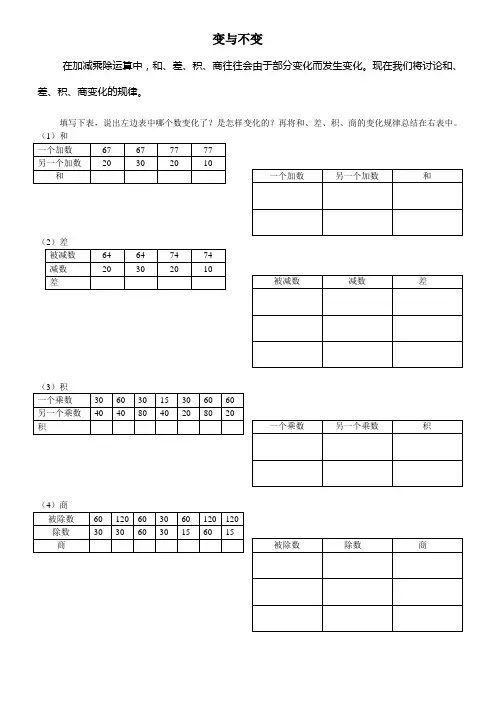
变与不变在加减乘除运算中，和、差、积、商往往会由于部分变化而发生变化。

现在我们将讨论和、差、积、商变化的规律。

填写下表，说出左边表中哪个数变化了？是怎样变化的？再将和、差、积、商的变化规律总结在右表中。

（1）和1、两个数相加，一个加数减少6，另一个加数增加6，和是否起变化？2、两个数相加，如果一个加数增加12，要使和增加三，那么另一个加数应有什么变化？3、两个数相减，如果被减数增加8，减数也增加8，差是否起变化？4、两个数相减，被减数减少16，如果要使差减少18，减数应有什么变化？5、两数相乘，如果一个乘数扩大4倍，另一个乘数缩小2倍，积将有什么变化？6、两数相乘，一个乘数扩大2倍，要使积扩大6倍，另一个乘数应该怎样变化？7、两数相除，如果被除数扩大4倍，除数缩小3倍，商将怎样变化？8、两个乘数相乘，积是60，如果一个乘数扩大2倍，另一个乘数缩小3倍，那么两个数的积是多少？练习1、两个数相加，一个加数增加3，另一个加数也增加3，和是否起变化？2、两个数相加，一个加数增加12，另一个加数减少12，和是否起变化？3、两个数相加，如果一个加数增加9，要使和增加12，那么，另一个加数应有什么变化？4、两个数相加，如果一个加数增加12，要使和减少6，那么，另一个加数应有什么变化？5、两数相减，被减数减少18，如果要使差不变，减数应有怎样的变化？6、两数相减，被减数增加5，如果要使差增加8，减数应有怎样的变化？7、两数相减，如果减数增加30，要使差不变，被减数应有什么变化？8、两数相减，如果减数增加32，要使差减少29，被减数应有怎样的变化？9、两数相乘，如果一个乘数扩大3倍，另一个乘数缩小3倍，积将怎样变化？10、两数相乘，一个乘数缩小3倍，要使积不变，另一个乘数应有什么变化？11、两数相乘，如果一个乘数缩小2倍，现在要使积扩大6倍，那么另一个乘数应有什么变化？12、两数相除，如果被除数扩大4倍，除数扩大2倍，商将怎样变化？13、两数相除，如果被除数扩大4倍，要使商扩大8倍，除数应有什么变化？14、两数相除，如果除数扩大6倍，要使商缩小36倍，被除数应怎样变化？15、两数相除，商为2400，如果被除数缩小40倍，除数扩大10倍，商就变为多少？。

思维训练第11讲变与不变学一学
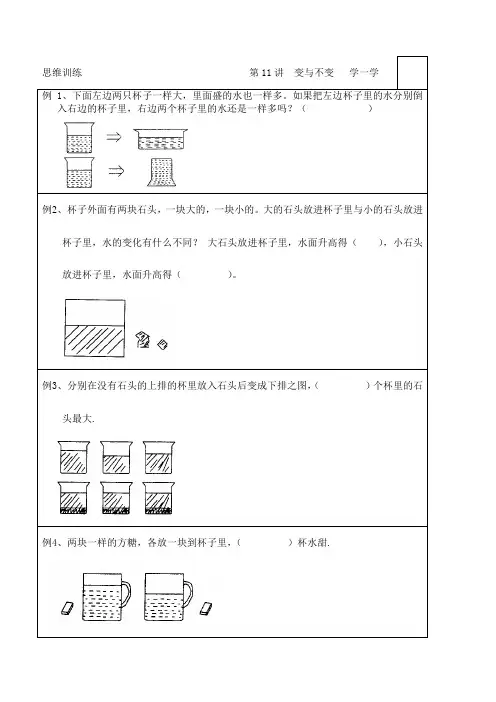
例1、下面左边两只杯子一样大，里面盛的水也一样多。

如果把左边杯子里的水分别倒入右边的杯子里，右边两个杯子里的水还是一样多吗？（）
例2、杯子外面有两块石头，一块大的，一块小的。

大的石头放进杯子里与小的石头放进杯子里，水的变化有什么不同？大石头放进杯子里，水面升高得（），小石头放进杯子里，水面升高得（）。

例3、分别在没有石头的上排的杯里放入石头后变成下排之图，（）个杯里的石头最大.
例4、两块一样的方糖，各放一块到杯子里，（）杯水甜.
例5、三杯糖水一样甜，哪杯水里放进去的糖最少？（）
做一做
1、两边的苹果个数等不等？（）
2、将大小不同的两块石头放入盛水相同的两个杯中，哪个杯中放入的是大石头？
（）
3、把鹅蛋、鸡蛋、鸽蛋分别放入三只碗里，猜猜它们分别放在（）只碗里.
4、3杯一样多的水中放入的糖块块数不同，哪一杯水更甜？（）。

变与不变
【专题导引】
【例1】下面左边两只杯子一样大，里面盛的水也一样多。

如果把左边杯子里的水分别倒入右边的杯子里，右边的两个杯子里的水还是一样多吗？
【试一试】两边的苹果个数等不等？
【例2】杯子外面有两块石头，一块大的，一块小的。

大的石头放进杯子里与小的石头放进杯子里，水的变化有什么不同？
【试一试】杯子外面有两块铁块，一块大的，一块小的，大铁块放进杯子里与小铁块放进杯子里，水的变化有什么不同？
【例3】分别在没有石头的上排的杯里放入石头后变成下排之图，哪个杯里的石头最大？
【试一试】分别在上排没有石头的杯子里各放一块铁块后变成下排的图，哪个杯子里面的铁块最小？
【例4】两块一样的方糖，各放一块到杯子里，哪杯水甜？
【试一试】在下面的4杯淡水中，每杯放进同样的2块方糖，哪一杯水最甜，为什么？
【＊例5】三杯糖水一样甜，哪杯水里放进去的糖最少？
【试一试】四杯糖水一样甜，哪杯水放进去的糖最少？。

一年级奥数培优专题第二章比一比看一看第一讲变与不变【专题导引】小朋友,你知道吗？把一块石头放进瓶子里,瓶子里的水会有什么变化？对了,瓶子里的水位就会升高。

把放进去的石头再拿出来,水又会怎样变化呢？下面,我们就来找一找变与不变的规律。

在某一物体中再添加一些物体,总量就会增加,在某一物体中取走一些物体,总量就会减少。

而仅仅是把物体改变它的形状或大小,质量就不会改变。

【专题导引】【例1】下面左边两只杯子一样大,里面盛的水也一样多。

如果把左边杯子里的水分别倒入右边的杯子里,右边的两个杯子里的水还是一样多吗？【试一试】两边的苹果个数等不等？【例2】杯子外面有两块石头,一块大的,一块小的。

大的石头放进杯子里与小的石头放进杯子里,水的变化有什么不同？【试一试】杯子外面有两块铁块,一块大的,一块小的,大铁块放进杯子里与小铁块放进杯子里,水的变化有什么不同？【例3】分别在没有石头的上排的杯里放入石头后变成下排之图,哪个杯里的石头最大？【试一试】分别在上排没有石头的杯子里各放一块铁块后变成下排的图,哪个杯子里面的铁块最小？【例4】两块一样的方糖,各放一块到杯子里,哪杯水甜？【试一试】在下面的4杯淡水中,每杯放进同样的2块方糖,哪一杯水最甜,为什么？【＊例5】三杯糖水一样甜,哪杯水里放进去的糖最少？【试一试】四杯糖水一样甜,哪杯水放进去的糖最少？课外作业家长签名：1、白球的个数和花球的个数一样多,如果把白球放入左边玻璃杯内,把花球放入右边杯内,左边杯里的白球多还是右边杯里的花球多？2、将大小不同的两块石头放入盛水相同的两个杯中,哪个杯中放入的是大石头？3、把鹅蛋、鸡蛋、鸽蛋分别放入三只碗里,猜猜它们分别放在哪只碗里？4、三杯一样多的水中放入的糖块块数不同,哪一杯水更甜？5、四杯盐水一样咸,哪一杯水里放进去的盐最多？我的学习收获：。

我来编题：。

第二讲移多补少【专题导引】如果有两组数量不同的物体,怎样才能使它们同样多呢？通过观察、比较,找出哪组多,多几个,然后把多的一部分平均分成两份,其中一份补给少的那一组,这样两组物体的数量同样多,这样做就是移多补少。