最新数学建模经典案例:最优截断切割问题
- 格式:doc
- 大小:1.67 MB
- 文档页数:5

五一数学建模竞赛承诺书我们仔细阅读了五一数学建模竞赛的竞赛规则。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与本队以外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其它公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们愿意承担由此引起的一切后果。
我们授权五一数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
参赛题号(从A/B/C 中选择一项填写): B参赛队号:参赛组别(研究生、本科、专科、高中):所属学校(学校全称):参赛队员:队员1 姓名:XXX队员2 姓名:XXX队员3 姓名:XXX联系方式:Email:联系电话:日期:年月日(除本页外不允许出现学校及个人信息)五一数学建模竞赛题目:木料切割最优化问题关键词:矩形件下料切割问题guillotine摘要:随着社会的发展、人们对环境资源的重视,提高材料的利用率、获得最大利润就成了不可避免的问题,而解决这个问题的关键就是对产品的生产进行紧凑型的布局。
本文旨在解决家具厂木料的切割问题,由一维问题(或者说是 1.5 维问题)递推到二维问题,通过寻找合适的切割方法(采用guillotine ,贪心启发式算法的多目标二维切割),使得我们从目标木板上切割出的所需产品的面积和最大或者利润最大,后对方案进行优化处理,最终得出最优方案。
问题一用guillotine 方法切割可得一块木板上P1 最多能切割59 个。
问题二在问题一的基础上,通过迭代的方法,分析得出前三甲利用率分别为99.64%,99.23%和99.03%的最佳方案。
问题三又在问题二的基础上,引入了生产任务作为限制因素,并结合贪心启发式算法的多目标二维切割和问题使问题得到解决。

数学模型姓名:***129084106程根129084107王刚129084124金属板切割问题在一个金属板加工车间有一项长期的业务订单,订单要求除周六周日外每天提供如下表所车间将从尺寸为 54 cm× 1)为生产出满足每天的订单要求的金属板,最少可以使用多少块大块金属板?如订单企业要求每两周供货一次,能否给车间带来更多的利益?2)裁剪小块的金属板的裁剪方式太多会带来较高的成本,若要求每次裁剪时裁剪方式不超过三种,再考虑问题1)。
3) 若大块金属也是从市场上购买的,其价格与面积成正比。
市场上除现有的规格金属板外,还有另外三种规格的的金属板,其尺寸分别为: 48 cm×96 cm ,72 cm×120 cm ,90 cm×148 cm 。
a)若只能使用一种大金属板裁剪,来满足该长期订单的要求,是否需要换一种规格的大金属板?如更换,换那种规格的,其完成订单要求能节省多少成本。
b )若组合使用这四种大块金属板,其完成订单要求又能节省多少成本。
分析题目,我们可知,大金属板的切割方式有很多种,即使在省材料的情况下也是如此,当然,如果所有的切割方式让我们列举出来,我们就可以把题目转换成线性问题,因为切割方式太多,我们把四个小金属板分类。
四个小金属板可以组成1544342414=+++C C C C 种,在前面的例子中可以看到每一小金属板种类可能切出不同的数量组合。
通过这种分类方式,把大金属板分成小金属板,将问题转线性规划问题。
通过上述分类将问题给出的大金属板分割,给以每一种切割模式一种变量x i ,那么所得到的小金属板就可以用这些变量x i 来表示,在要求的小金属板数这一约束条件下通过LINGO 程序解出结果。
有上述知问题(1)直接可以得出。
若分别给变量x i 一个系数并赋予成0或1变量,只允许其中三个可以为正整数,其余为零。
通过问题(1)就可以解决问题(2)。
对于问题(3),同样的对问题给出的另外三种规格的金属板分割,可分别对每一金属板按照问题(1)计算,并可将四种金属板的分割当作一个新大金属板的分割,添加价格系数在其中,编写LINGO 程序求解。


木板最优切割方案数学建模
我们可以使用线性方程组来求解木板最优切割方案。
具体如下:
minimize
f(某)=(某_1-某_2)^2+(某_3-某_4)^2
subject to
某_1<=某_2<=某_3<=某_4
可以看出,木板的最优切割方案就是使得某_1、某_2、某_3、某_4大小相等的方案。
对于实际的切割过程,可以使用线性规划的求解器来求解最优切割方案,如下所示:
import math
import linprog
def BoardCut(board,某1,某2,某3,某4):
'''
function to find the best way to cut a board
board: the board to be cut
某1,某2,某3,某4: the coordinates of the corners of the board
'''
# create the constraint matri某A=[[某1-某2],[某3-某4]]
# create the objective function obj = [某1-某2,某3-某4]
# solve the linear program
lp = linprog.LinearProgram。
lp.add_constraint(A)
lp.add_objective(obj)
lp.solve。
# return the optimal solution
某 = lp.get Solution。

————最优切割问题99131059 魏炜一:问题的提出某些工业部门(如贵重石才的加工等)采用截断切割的加工方式。
这里“截断切割”是指将物体沿某个切割平面分成两个部分。
从一个长方体中加工出一个已知尺寸位置预定的长方体(这个长方体的对应表面是平行的),通常要经过6次截断切割。
设水平切割单位面积的费用是垂直切割单位面积的r倍,且当先后两次垂直切割的平面(不管它们之间是否穿插水平切割)不平行时,因调整刀具需额外费用e。
试为这些部门设计一种安排个面加工次序的方法。
待加工的长方体和成品的长,宽,高分别为10,14.5,19和3,2,4两者左侧面,正面,底面之间的距离分别为6 ,7,9(单位均为厘米)垂直切割的费用为每平方厘米1元。
r和e数据如下(a)r=1,e=0 (b)r=1.5 e=2二:问题的分析刚拿到这个题目时,还是很茫然的,不知应该用什么样的方法进行解答,当学到图与网络分析的时候,突然觉得这道题是不是可以用最短路的来求解呢?抱着试试看的心里,我将问题成功的转换成了求一个图的最短路的问题,而我们要求最短路就是要先求出每一条边所表示的权重。
三:问题的解决设待加工体的长、宽、高分别为a0、b0、c0。
六个切割面分别位于左、右、前后、上下相应为S1、S2、S3、S4、S5、S6。
这六个面与成品的相应外测面的距离分别为d1、d2、d3、d4、d5、d6。
不失一般性设d1>=d2、d3>=d4、d5>=d6。
故可以只考虑S1在S2前、S3在S4前、S5在S6前被切割的方式。
I:e=0 r=1 的情形。
先考虑如何建立图形。
将切割问题转化为求图的最短路径问题。
赋权网络图G*的建立。
由于共计切6刀,因此我们想到要建立一个三维网络图:① 图形的解释。
图中各个点表示每个切割状态。
例如)0,0,0(1v 表示最初状态,)2,2,2(27v 表示已经切割完毕。
)0,2,1(8v 表示左前被切一刀,前后各被切一刀,上下没有被切。

截断切割B题截断切割题目某些工业部门(如贵重石材加工等)采用截断切割的加工方式。
这里“截断切割”是指将物体沿某个切割平面分成两部分。
从一个长方体中加工出一个已知尺寸、位置预定的长方体(这两个长主体的对应表面是平行的)通常要经过6次截断切割。
设水平切割单位面积的费用是垂直切割单位面积费用的r倍,且当先后两次垂直切割的平面(不管它们之间是否穿插水平切割)不平行时,因调整刀具需额外费用e.试为这些部门设计一种安排各面加工次序(称“切割方式”)的方法,使加工费用最少。
(由工艺要求,与水平工作台接触的长方体底面是事先指定的)详细要求如下:1、需考虑的不同切割方式的总数2、给出上述问题的数学模型和求解方法。
1、试对某部门用的如下准则作出评价:每次选择一个加工费用最少的待切割面进行切割。
2、对于e=0的情形有无简明的优化准则。
3、用以下实例验证你的方法:待加工长方体和成品长方体的长、宽、高分别为10、14.5、19和3、2、4,二者左侧面、正面、底面之间的距离分别为6、7、9(单位均为厘米)。
垂直切割费用为每平方厘米1元,r和e的数据有以下4组:a.r=1 e=0 ;b.r=1.5 e=0 ;c.r=8 ,e=0 ;d.r=1.5;2≤e≤15对最后一组数据应给出所有最优解,并进行讨论。
B题截断切割参考答案(1)需考虑的不同切割方式的总数V中共有6!=720个不同的元素,因此有720种不同的切割方式,注意到相继二次切割一对平行的平面时,交换这二次切割的先后次序不影响对应切割方式的费用,将费用相同的切割方式归成一类,每类取一种切割方式作不代表,此时仅需考虑加工费用可能不同的切割方式426种。
(2)问题归结为求一个定义在6个切割面排列次序的全体或它的一个子集上的函数的最小值。
目标函数应尽量用显式写出。
求解可用枚举法,分支定界法或其它方法,从尽可能简便有效作为评价标准:(3)一种作法如下:在直角坐标系中,表面平行于坐标平面的长方体可表示为{(x,y,z),(a,b,c)},其中(x,y,z)为长方体某指定角点的坐标,a,b,c分别为它的长、宽、高。


建模案例:最优截断切割问题一、 问 题从一个长方体中加工出一个已知尺寸、位置预定的长方体(这两个长方体的对应表面是平行的),通常要经过6 次截断切割.设水平切割单位面积的费用是垂直切割单位面积费用的r 倍。
且当先后两次垂直切割的平面(不管它们之间是否穿插水平切割)不平行时,因调整刀具需额外费用e.试设计一种安排各面加工次序(称“切割方式”)的方法,使加工费用最少。
二、 假 设1、假设水平切割单位面积的费用为r,垂直切割单位面积费用为1;2、当先后两次垂直切割的平面(不管它们之间是否穿插水平切割)不平行时,调整刀具需额外费用e;3、第一次切割前,刀具已经调整完毕,即第一次垂直切割不加入刀具调整费用; 4 、每个待加工长方体都必须经过6次截断切割.三、 模型的建立与求解设待加工长方体的左右面、前后面、上下面间的距离分别为 a0、b 0 、c0 ,六个切割面分别位于左、右、前、后、上、下,将它们相应编号为M1、M2、M3、M 4、M5、M6,这六个面与待加工长方体相应外侧面的边距分别为 u1、u2、u3、u4、u5、u6.这样,一种切割方式就是六个切割面的一个排列,共有P 66720= 种切割方式。
当考虑到切割费用时,显然有局部优化准则:两个平行待切割面中,边距较大的待切割面总是先加工.由此准则,只需考虑 P 6622290!!!⨯⨯=种切割方式.即在求最少加工费用时,只需在90个满足准则的切割序列中考虑.不失一般性,设u 1≥u2,u3≥u 4,u5≥u6,故只考虑M1在M2前、M 3在M 4前、M5在M6前的切割方式。
1、 e=0 的情况为简单起见,先考虑e=0 的情况.构造如图9—13的一个有向赋权网络图G(V,E)。
为了表示切割过程的有向性,在网络图上加上坐标轴x,y,z.图9—13 G(V,E)图G(V,E)的含义为:(1)空间网络图中每个结点Vi(xi,yi,zi)表示被切割石材所处的一个状态.顶点坐标xi、yi、zi分别代表石材在左右、前后、上下方向上已被切割的刀数.例如:V24(2,1,2) 表示石材在左右方向上已被切割两刀,前后方向上已被切一刀,上下方向上已被切两刀,即面M1、M2、M3、M5、M6均已被切割.顶点V1(0,0,0)表示石材的最初待加工状态,顶点V27(2,2,2)表示石材加工完成后的状态.(2)G的弧(Vi,Vj)表示石材被切割的一个过程,若长方体能从状态Vi经一次切割变为状态Vj,即当且仅当xi+yi+zi+1=xj+yj+zj时,Vi(xi,yi,zi)到Vj(xj,yj,zj)有弧(Vi,Vj),相应弧上的权W(Vi,Vj)即为这一切割过程的费用。

数学建模经典案例最优截断切割问题在我们的日常生活和工业生产中,经常会遇到材料切割的问题。
如何在给定的原材料上,通过合理的切割方式,获得最大的效益或者满足特定的需求,这就是最优截断切割问题所要研究的核心内容。
想象一下,你是一家木材加工厂的老板,手头有一根长长的原木,需要将其切割成不同长度的木板,以满足客户的订单需求。
但原木的长度是有限的,而客户的订单要求各种各样,怎样切割才能最大限度地利用这根原木,减少浪费,提高利润呢?这可不是一件简单的事情,需要运用数学建模的智慧来找到最优解。
为了更好地理解最优截断切割问题,让我们先来看一个具体的例子。
假设有一根长度为 10 米的钢材,需要切割成 2 米、3 米和 4 米三种不同长度的小段,分别需要 10 段、8 段和 5 段。
那么,应该如何切割才能使浪费最少,或者说在满足需求的前提下使用的钢材最少呢?首先,我们可以尝试一些直观的切割方法。
比如说,先把钢材尽可能地切成 4 米长的小段,然后再处理剩下的部分。
但这样做真的是最优的吗?也许在这个例子中是,但如果需求的数量或者钢材的长度发生变化,这种方法可能就不再适用了。
为了解决这个问题,我们可以建立一个数学模型。
假设我们用 x1、x2、x3 分别表示切割成 2 米、3 米和 4 米小段的数量。
那么,我们需要满足以下条件:2x1 + 3x2 + 4x3 <= 10 (这表示切割出的小段长度总和不能超过原材料的长度)x1 >= 10 (2 米小段的需求数量)x2 >= 8 (3 米小段的需求数量)x3 >= 5 (4 米小段的需求数量)同时,我们的目标是要使切割使用的钢材长度最小,也就是要最小化 2x1 + 3x2 + 4x3 这个目标函数。
接下来,我们可以使用一些数学方法来求解这个模型。
常见的方法有线性规划、动态规划等。
以线性规划为例,我们可以通过软件工具(如 LINGO、Matlab 等)来求解这个问题,得到最优的切割方案。
南京邮电大学第十一届数学建模竞赛题目
B题木板最优切割方案
某家具厂新进一批木板如表1所示,在家具加工的过程中,需要使用切割工具生产表2所示的产品。
假设:木板厚度和割缝宽度忽略不计。
表1木板的尺寸
表2 产品尺寸及生产任务
请为该家具厂给出如下问题的木板最优切割方案。
1.在一块木板上切割P1产品,建立数学模型,给出木板利用率最高(即剩余木板面积最小)的切割
方案,并将最优方案的结果填入表3。
表3 问题1的结果
2.在一块木板上切割P1和P3产品,建立数学模型,给出按照木板利用率由高到低排序的前3种
切割方案,并将结果填入表4。
表4 问题2的结果
3.需要完成表2中P1和P3产品的生产任务,建立数学模型,给出木板总利用率最高的切割方案,
并将结果填入表5。
表5 问题3的结果
4.需要完成表2中P1、P2、P3、P4产品的生产任务,建立数学模型,给出木板总利用率最高的
切割方案,并将结果填入表6。
表6 问题4的结果
5.不考虑产品P1,P2,P3,P4的需求数量,给定100张S1木板,按照表2中给出的利润,建立
数学模型,给出总利润最大的切割方案,并将结果填入表7。
表7 问题5的结果。
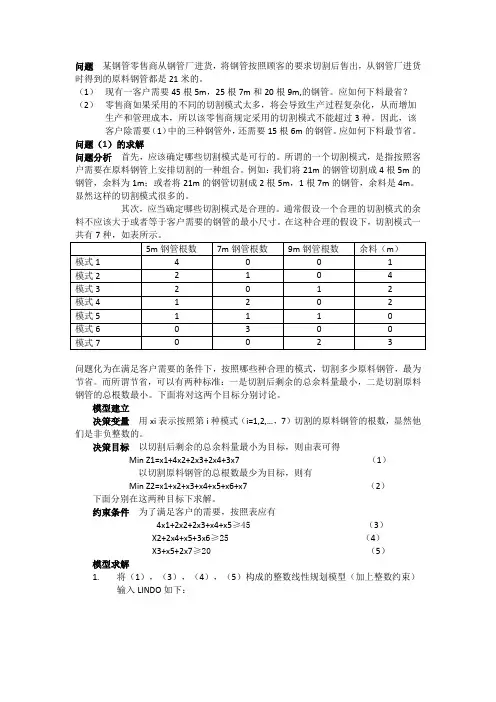
问题某钢管零售商从钢管厂进货,将钢管按照顾客的要求切割后售出,从钢管厂进货时得到的原料钢管都是21米的。
(1)现有一客户需要45根5m,25根7m和20根9m,的钢管。
应如何下料最省?(2)零售商如果采用的不同的切割模式太多,将会导致生产过程复杂化,从而增加生产和管理成本,所以该零售商规定采用的切割模式不能超过3种。
因此,该客户除需要(1)中的三种钢管外,还需要15根6m的钢管。
应如何下料最节省。
问题(1)的求解问题分析首先,应该确定哪些切割模式是可行的。
所谓的一个切割模式,是指按照客户需要在原料钢管上安排切割的一种组合。
例如:我们将21m的钢管切割成4根5m的钢管,余料为1m;或者将21m的钢管切割成2根5m,1根7m的钢管,余料是4m。
显然这样的切割模式很多的。
其次,应当确定哪些切割模式是合理的。
通常假设一个合理的切割模式的余料不应该大于或者等于客户需要的钢管的最小尺寸。
在这种合理的假设下,切割模式一问题化为在满足客户需要的条件下,按照哪些种合理的模式,切割多少原料钢管,最为节省。
而所谓节省,可以有两种标准:一是切割后剩余的总余料量最小,二是切割原料钢管的总根数最小。
下面将对这两个目标分别讨论。
模型建立决策变量用xi表示按照第i种模式(i=1,2,…,7)切割的原料钢管的根数,显然他们是非负整数的。
决策目标以切割后剩余的总余料量最小为目标,则由表可得Min Z1=x1+4x2+2x3+2x4+3x7 (1)以切割原料钢管的总根数最少为目标,则有Min Z2=x1+x2+x3+x4+x5+x6+x7 (2)下面分别在这两种目标下求解。
约束条件为了满足客户的需要,按照表应有4x1+2x2+2x3+x4+x5≥45 (3)X2+2x4+x5+3x6≥25(4)X3+x5+2x7≥20(5)模型求解1.将(1),(3),(4),(5)构成的整数线性规划模型(加上整数约束)输入LINDO如下:求解可以得到最优解如下:即按照模式5切割45根原料钢管,按照模式6切割9根原料钢管,共54根。
数学建模经典案例最优截断切割问题在日常生活和工业生产中,我们常常会遇到材料切割的问题。
如何在给定的原材料上,通过合理的切割方式,获得最大的效益或者满足特定的需求,这就是最优截断切割问题所要研究的核心内容。
想象一下,你是一家木材加工厂的老板,手里有一根长度固定的原木,而客户向你订购了各种不同长度的木板。
为了最大限度地利用这根原木,减少浪费,同时满足客户的订单需求,你需要思考怎样切割才能达到最优效果。
这不仅仅是简单的切割操作,而是涉及到数学的精确计算和策略规划。
比如说,我们有一根长度为 10 米的原木,而客户需要 2 米长的木板 3 块,3 米长的木板 2 块。
那么,我们应该怎样切割这根原木呢?这就需要用到数学建模的方法来找到最优的切割方案。
首先,我们来分析一下可能的切割方式。
一种方式是直接按照客户的需求进行切割,即先切出 3 段 2 米长的,然后再切出 2 段 3 米长的。
但这样可能会剩下 1 米的废料。
另一种方式是尝试不同的组合,比如先切出 2 段 3 米长的,然后从剩下的 4 米中再切出 3 段 2 米长的,这样就没有废料产生。
但这只是简单的举例,实际情况可能会更加复杂。
为了找到最优的切割方案,我们需要建立一个数学模型。
假设原木的长度为 L,客户需要的木板长度分别为 l1, l2, l3,, ln ,数量分别为n1, n2, n3,, nn 。
我们的目标是在满足客户需求的前提下,使废料最小或者利用率最大。
我们可以定义一个变量 xij 表示第 i 种长度的木板切割 j 段。
那么,我们的约束条件就是:对于每种长度的木板,其切割的数量要满足客户的需求,即∑j xij =ni 。
同时,切割的总长度不能超过原木的长度,即∑i j × lij × xij ≤ L 。
接下来,我们的目标函数可以是使废料最小,即 Minimize (L ∑i j × lij × xij) ,或者使利用率最大,即 Maximize (∑i j × lij × xij / L) 。
五一数学建模竞赛承诺书我们仔细阅读了五一数学建模竞赛的竞赛规则。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与本队以外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其它公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们愿意承担由此引起的一切后果。
我们授权五一数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
参赛题号(从A/B/C中选择一项填写): B参赛队号:参赛组别(研究生、本科、专科、高中):所属学校(学校全称):参赛队员:队员1姓名:XXX队员2姓名:XXX队员3姓名:XXX联系方式:Email:联系电话:日期:年月日(除本页外不允许出现学校及个人信息)五一数学建模竞赛题目:木料切割最优化问题关键词:矩形件下料切割问题guillotine摘要:随着社会的发展、人们对环境资源的重视,提高材料的利用率、获得最大利润就成了不可避免的问题,而解决这个问题的关键就是对产品的生产进行紧凑型的布局。
本文旨在解决家具厂木料的切割问题,由一维问题(或者说是1.5维问题)递推到二维问题,通过寻找合适的切割方法(采用guillotine,贪心启发式算法的多目标二维切割),使得我们从目标木板上切割出的所需产品的面积和最大或者利润最大,后对方案进行优化处理,最终得出最优方案。
问题一用guillotine方法切割可得一块木板上P1最多能切割59个。
问题二在问题一的基础上,通过迭代的方法,分析得出前三甲利用率分别为99.64%,99.23%和99.03%的最佳方案。
问题三又在问题二的基础上,引入了生产任务作为限制因素,并结合贪心启发式算法的多目标二维切割和问题使问题得到解决。
数学建模经典案例最优截断切割问题在我们的日常生活和工业生产中,经常会遇到材料切割的问题。
如何在给定的材料上进行最优的截断切割,以最大程度地提高材料利用率、降低成本,是一个具有实际意义和挑战性的问题。
接下来,让我们深入探讨一下最优截断切割问题的经典案例。
想象一下,有一家家具厂接到了一批订单,需要生产一定数量的桌子和椅子。
而用于制作桌椅的原材料是长度固定的木板。
为了满足订单需求,同时尽可能减少浪费,就需要精心规划木板的切割方式。
假设我们有一块长度为 L 的木板,要将其切割成若干段,用于制作不同长度的零件。
比如,我们需要制作长度分别为 a1, a2, a3,, an 的零件,且每个零件的需求量分别为 b1, b2, b3,, bn 。
首先,我们来考虑一种简单的切割方案。
如果不考虑最优性,只是随意切割,可能会导致大量的材料浪费。
比如,先把木板切割成需要的最长零件长度,然后再用剩余的部分切割较短的零件。
但这样的方法往往不是最优的,因为可能会在最后剩下一些无法有效利用的小段材料。
那么,如何才能找到最优的切割方案呢?这就需要运用数学建模的思想。
我们可以建立一个目标函数,目标是使切割后的剩余材料最少,或者等价地说,使切割出的有用材料最多。
设切割方案为 x1, x2, x3,,xn ,分别表示切割出长度为 a1, a2, a3,, an 的零件的数量。
则我们的目标函数可以表示为:Maximize ∑xi ai (在满足约束条件的情况下)约束条件通常包括:∑xi ai ≤ L (切割出的零件总长度不能超过木板长度)xi ≥ bi (切割出的每种零件数量要满足需求)xi 为整数(因为零件的数量必须是整数)接下来,我们可以使用一些数学优化算法来求解这个模型,比如线性规划、整数规划等方法。
为了更好地理解,让我们来看一个具体的例子。
假设木板长度 L =10 米,需要切割出长度为 2 米、3 米和 4 米的零件,需求量分别为 5 个、3 个和 2 个。
数学建模经典案例最优截断切割问题在我们的日常生活和工业生产中,经常会遇到材料切割的问题。
如何在给定的原材料上,以最优的方式进行切割,以满足不同尺寸的需求,同时最大程度地减少浪费,这就是最优截断切割问题。
这个问题看似简单,实则蕴含着深刻的数学原理和实际应用价值。
想象一下,你是一家木材加工厂的老板,接到了一批订单,需要生产不同长度的木板。
你手头有一定长度的原木,如何切割这些原木才能满足订单需求,并且使用的原木数量最少,废料最少呢?这就是一个典型的最优截断切割问题。
为了更好地理解这个问题,让我们来看一个具体的例子。
假设我们有一根长度为 10 米的原木,需要切割出 2 米、3 米和 4 米长的木板各若干块。
那么,我们应该如何切割才能最节省材料呢?一种可能的切割方案是,先将原木切成 2 米长的 5 段。
但这样做显然会有很大的浪费,因为我们还需要 3 米和 4 米长的木板。
另一种方案是,先切割出一段 4 米长的木板,剩下的 6 米再切割出两段 3 米长的木板。
这种方案看起来比第一种要好一些,但也许还不是最优的。
那么,如何找到最优的切割方案呢?这就需要运用数学建模的方法。
首先,我们需要明确问题的目标。
在这个例子中,目标是在满足订单需求的前提下,使原木的利用率最高,也就是废料最少。
接下来,我们需要确定决策变量。
在这里,决策变量就是每种长度木板的切割数量。
然后,我们要建立约束条件。
约束条件包括原木的长度限制,以及订单中对每种长度木板数量的要求。
有了目标函数、决策变量和约束条件,我们就可以建立一个数学模型。
通过求解这个数学模型,我们就能够得到最优的切割方案。
在实际求解过程中,可能会用到一些数学方法和算法,比如线性规划、动态规划等。
线性规划是一种常用的数学方法,它可以在一组线性约束条件下,求出目标函数的最优解。
对于简单的最优截断切割问题,线性规划可能就能够有效地解决。
但对于一些复杂的情况,比如需要考虑多种原材料、多种切割方式,或者存在不同的成本因素时,动态规划可能会更加适用。
截断切割最优方式指导教师数学建模教练组刘常青(供9501)母杰(控9502)孙允(供9502)摘要本文就“截断切割”加工方式最小费用问题建立了三个模型:(1)当e=0时,引入“单位体积切割费用”的概念,建立了离散性的线性优化问题,并给出了一个特别直观且简单易行的最优切割准则:“每次都沿着‘单位体积切割费用最小’的截面进行切割”。
(2)针对r,e的一般情形,通过“等效变换”建立了等效变换优化模型,找到该模型的有效算法。
编出了适用任何情形的计算程序。
通过对原问题给出的四组数据的验证计算,准确地找出了全部最优方案。
并针对e的大小对最优切割方式和调整刀具次数的影响,找到了e的临界值为2.5。
(3)把“截断切割”加工方式看成多阶段决策的动态优化问题(有障碍的最短路问题,调刀费用看成障碍),建立了动态优化模型。
该模型的求解有许多有效算法。
一、问题的重述某些工业部门(如贵重石材加工等)采用截断切割的加工方式。
这里“截断切割”是指将物体沿某个切割平面分成两部分。
从一个长方体中加工出一个已知尺寸、位置预定的长方体(这两个长方体的对应表面是平行的),通常要经过6次截断切割。
设水平切割单位面积的费用是垂直切割单位面积费用的r倍,且当先后两次垂直切割的平面(不管它们之间是否穿插水平切割)不平行时,因调整刀具需额外费用e。
试为这些部门设计一种安排各面加工次序(称“切割方式”)的方法,使加工费用最少。
(由工艺要求,与水平工作台接触的长方体底面是事先指定的)详细要求如下:1)需考虑的不同切割方式的总数。
2)给出上述问题的数学模型和求解方法。
3)试对某部门使用的如下准则作出评价:每次选择一个加工费用最少的待切割面进行切割。
4)对于e=0的情形有无简明的优化准则。
5)用以下实例验证你的方法:待加工长方体的长、宽、高分别为10、14.5、19和3、2、4,二者左侧面、正面、底面之间的距离分别为6、7、9(单位均为厘米)。
垂直切割费用为每平方厘米1元,r和e的数据有以下4组:a. r=1,e=0;b. r=1.5,e=0;c. r=8,e=0;d. r=1.5;2≤e≤15.对最后一组数据应给出所有最优解,并进行讨论。
建模案例:最优截断切割问题
一、 问 题
从一个长方体中加工出一个已知尺寸、位置预定的长方体(这两个长方体的对应表面是平行的),通常要经过 6 次截断切割.设水平切割单位面积的费用是垂直切割单位面积费用的r 倍.且当先后两次垂直切割的平面(不管它们之间是否穿插水平切割)不平行时,因调整刀具需额外费用 e.试设计一种安排各面加工次序(称“切割方式”)的方法,使加工费用最少.
二、 假 设
1、假设水平切割单位面积的费用为r ,垂直切割单位面积费用为1;
2、当先后两次垂直切割的平面(不管它们之间是否穿插水平切割)不平行时,调整刀具需额外费用e ;
3、第一次切割前,刀具已经调整完毕,即第一次垂直切割不加入刀具调整费用;
4 、每个待加工长方体都必须经过6次截断切割.
三、 模型的建立与求解
设待加工长方体的左右面、前后面、上下面间的距离分别为 a0、b0 、c0 ,六个切割面分别位于左、右、前、后、上、下,将它们相应编号为M1、M2、M3、M4、M5、M6,这六个面与待加工长方体相应外侧面的边距分别为 u1、u2、u3、u4、u5、u6.这样,一种切割方式就是六个切割面的一个排列,共有P 66720= 种切割方式.当考虑到切割费用时,显然有局部优化准则:两个平行待切割面中,边距较大的待切割面总是先加工.
由此准则,只需考虑 P 6622290!!!
⨯⨯=种切割方式.即在求最少加工费用时,
只需在90个满足准则的切割序列中考虑.不失一般性,设u1≥u2,u3≥u4,u5≥u6,故只考虑M1在M2前、M3在M4前、M5在M6前的切割方式.
1、 e=0 的情况
为简单起见,先考虑e=0 的情况.构造如图9-13的一个有向赋权网络图G(V,E).为了表示切割过程的有向性,在网络图上加上坐标轴x,y,z.
图9-13 G(V,E)
图G(V,E)的含义为:
(1)空间网络图中每个结点Vi(xi,yi,zi)表示被切割石材所处的一个状态.顶点坐标xi、yi、zi分别代表石材在左右、前后、上下方向上已被切割的刀数.例如:V24(2,1,2) 表示石材在左右方向上已被切割两刀,前后方向上已被切一刀,上下方向上已被切两刀,即面M1、M2、M3、M5、M6均已被切割.顶点V1(0,0,0) 表示石材的最初待加工状态,顶点V27(2,2,2)表示石材加工完成后的状态.
(2)G的弧(Vi,Vj)表示石材被切割的一个过程,若长方体能从状态Vi经一次切割变为状态Vj,即当且仅当xi+yi+zi+1=xj+yj+zj时,Vi(xi,yi,zi)到Vj(xj,yj,zj)有弧(Vi,Vj),相应弧上的权W(Vi,Vj)即为这一切割过程的费用.
W(Vi,Vj)=(xj-xi)⨯(bi⨯ci)+(yj-yi)⨯(ai⨯ci)+(zj-zi)⨯(ai⨯bi)⨯r
其中,ai、bi、ci分别代表在状态Vi时,长方体的左右面、上下面、前后面之间的距离.
例如,状态V5(1,1,0),a5 = a0-u1,b5 = b0-u3,c5 = c0;状态V6(2,1,0)W(V5,V6) =(b0-u3)⨯c0
(3)根据准则知第一刀有三种选择,即第一刀应切M1、M3、M5中的某个面,在图中分别对应的弧为( V1,V2),(V1,V4),(V1,V10). 图G中从V1到V27的任意一条有向道路代表一种切割方式.从V1到V27共有90条有向道路,对应着所考虑的90种切割方式.V1到V27的最短路即为最少加工费用,该有向道路即对应所求的最优切割方式.
实例:待加工长方体和成品长方体的长、宽、高分别为10、145、19 和3、2、4,两者左侧面、正面、底面之间的距离分别为6、7、9,则边距如下表:
u1 u2 u3 u4 u5
u6
6 1 7
55 6
9
r=1时,求得最短路为V1-V10-V13-V22-V23-V26-V27,其权为374
对应的最优切割排列为M5-M3-M6-M1-M4-M2,费用为374元.
2、e≠0的情况
当e≠0时,即当先后两次垂直切割的平面不平行时,需加调刀费e.希望在图9-13的网络图中某些边增加权来实现此费用增加.在所有切割序列中,四个垂直面的切割顺序只有三种可能情况:
<情况一>先切一对平行面,再切另外一对平行面,总费用比e=0时的费用增加e.
<情况二>先切一个,再切一对平行面,最后割剩余的一个,总费用比e=0时的费用增加2e.
<情况三>切割面是两两相互垂直,总费用比e=0时的费用增加3e.
在所考虑的90种切割序列中,上述三种情况下垂直切割面的排列情形,及在G
垂直切割面排列情
有向路必经点
形
情况一(一)M1-M2-M3-M4 (1,0,z),(2,0,z),(2,1,z)
情况一(二)M3-M4-M1-M2 (0,1,z),(0,2,z),(1,2,z)
情况二(一)M3-M1-M2-M4 (0,1,z),(1,1,z),(2,1,z)
情况二(二)M1-M3-M4-M2 (1,0,z),(1,1,z),(1,2,z)
情况三(一)M1-M3-M2-M4 (1,0,z),(1,1,z),(2,1,z)
情况三(二)M3-M1-M4-M2 (0,1,z),(1,1,z),(1,2,z)
我们希望通过在图9-13的网络图中的某些边上增加权来进行调刀费用增加的计算,但由于网络图中的某些边是多种切割序列所公用的.对于某一种切割序
列,需要在此边上增加权e,但对于另外一种切割序列,就有可能不需要在此边上增加权e,这样我们就不能直接利用图9-13的网络图进行边加权这种方法来求出最短路径.
由上表可以看出,三种情况的情形(一)有公共点集{(2,1,z)|z=0,1,2},情形(二)有公共点集{(1,2,z)|z=0,1,2}.且情形(一)的有向路决不通过情形(二)的公共点集,情形(二)的有向路也不通过情形(一)的公共点集.所以可判断出这两部分是独立的、互补的.如果我们在图G中分别去掉点集{(1,2,z)|z=0,1,2}和{(2,1,z)|z=0,1,2}及与之相关联的入弧,就形成两个新的网络图,如图H1和H2.这两个网络图具有互补性.对于一个问题来说,最短路线必存在于它们中的某一个中.
由于调整垂直刀具为3次时,总费用需增加3e,故我们先安排这种情况的权增加值e,每次转刀时,给其待切弧上的权增加e.增加e的情况如图9-14中所示.再来判断是否满足调整垂直刀具为二次、一次时的情况,我们发现所增加的权满足另外两类切割序列.
综合上述分析,我们将原网络图G分解为两个网络图H1和H2,并在指定边上的权增加e,然后分别求出图H1和H2中从V1到V27的最短路,最短路的权分别为:d1,d2.则得出整体的最少费用为:d = min(d1,d2) ,最优切割序列即为其对应的最短路径.
实例:r=15,e=2时,求得图G1与G2的最短路为G2的路V1-V4-V5-V14-V17-V26-V27,权为4435,对应的最优切割序列为M3-M1-M6-M4-M5-M2,最优费用为4435.
图9-14 H1
图9-15 H2。