数学建模案例分析最短路问题
- 格式:ppt
- 大小:7.60 MB
- 文档页数:38




实验名称:第十一章最短路问题一、实验内容与要求掌握Dijkstra算法和Floyd算法,并运用这两种算法求一些最短路径的问题.二、实验软件MATLAB7.0三、实验内容1、在一个城市交通系统中取出一段如图所示,其入口为顶点v1,出口为顶点v8,每条弧段旁的数字表示通过该路段所需时间,每次转弯需要附加时间为3,求v1到v8的最短时间路径.63V4 2 V7 4 V8程序:function y=bijiaodaxiao(f1,f2,f3,f4)v12=1;v23=3;v24=2;v35=1;v47=2;v57=2;v56=6;v68=3;v78=4;turn=3;f1=v12+v23+v35+v56+turn+v68;f2=v12+v23+v35+turn+v57+turn+v78;f3=v12+turn+v24+turn+v47+v78;f4=v12+turn+v24+v47+turn+v57+turn+v56+turn+v68;min=f1;if f2<minmin=f2;endif f3<minmin=f3;endif f4〈minmin=f4;endminf1f2f3f4实验结果:v1到v8的最短时间路径为15,路径为1—2-4-7-8.2、求如图所示中每一结点到其他结点的最短路。
V110 V3V59 V6function[D,R]=floyd(a)n=size(a,1);D=afor i=1:nfor j=1:nR(i,j)=j;endendRfor k=1:nfor i=1:nfor j=1:nif D(i,k)+D(k,j)<D(i,j)D(i,j)=D(i,k)+D(k,j);R(i,j)=R(i,k);endendendkDRend程序:>〉a=[0 3 10 inf inf inf inf inf;3 0 inf 5 inf inf inf inf;10 inf 0 6 inf inf inf inf;inf 5 6 0 4 inf 10 inf ;inf inf inf 4 0 9 5 inf ;inf inf inf inf 9 0 3 4;inf inf inf 10 5 3 0 6;inf inf inf inf inf 4 6 0;];[D,R]=floyd(a)实验结果:D =0 3 10 Inf Inf Inf Inf Inf3 0 Inf 5 Inf Inf Inf Inf10 Inf 0 6 Inf Inf Inf InfInf 5 6 0 4 Inf 10 InfInf Inf Inf 4 0 9 5 InfInf Inf Inf Inf 9 0 3 4Inf Inf Inf 10 5 3 0 6Inf Inf Inf Inf Inf 4 6 0R =1 2 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 8k =1D =0 3 10 Inf Inf Inf Inf Inf3 0 13 5 Inf Inf Inf Inf10 13 0 6 Inf Inf Inf InfInf 5 6 0 4 Inf 10 InfInf Inf Inf 4 0 9 5 InfInf Inf Inf Inf 9 0 3 4Inf Inf Inf 10 5 3 0 6Inf Inf Inf Inf Inf 4 6 0R =1 2 3 4 5 6 7 81 2 1 4 5 6 7 81 1 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 8 k =2D =0 3 10 8 Inf Inf Inf Inf3 0 13 5 Inf Inf Inf Inf10 13 0 6 Inf Inf Inf Inf8 5 6 0 4 Inf 10 InfInf Inf Inf 4 0 9 5 InfInf Inf Inf Inf 9 0 3 4Inf Inf Inf 10 5 3 0 6Inf Inf Inf Inf Inf 4 6 0R =1 2 3 2 5 6 7 81 2 1 4 5 6 7 81 1 3 4 5 6 7 82 234567 81 2 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 8 k =3D =0 3 10 8 Inf Inf Inf Inf3 0 13 5 Inf Inf Inf Inf10 13 0 6 Inf Inf Inf Inf8 5 6 0 4 Inf 10 InfInf Inf Inf 4 0 9 5 InfInf Inf Inf Inf 9 0 3 4Inf Inf Inf 10 5 3 0 6Inf Inf Inf Inf Inf 4 6 0R =1 2 3 2 5 6 7 81 2 1 4 5 6 7 81 1 3 4 5 6 7 82 234567 81 2 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 8k =4D =0 3 10 8 12 Inf 18 Inf3 0 11 5 9 Inf 15 Inf10 11 0 6 10 Inf 16 Inf8 5 6 0 4 Inf 10 Inf12 9 10 4 0 9 5 InfInf Inf Inf Inf 9 0 3 418 15 16 10 5 3 0 6Inf Inf Inf Inf Inf 4 6 0R =1 2 3 2 2 6 2 81 2 4 4 4 6 4 81 4 3 4 4 6 4 82 234567 84 4 4 4567 81 2 3 4 5 6 7 84 4 4 4567 81 2 3 4 5 6 7 8 k =5D =0 3 10 8 12 21 17 Inf3 0 11 5 9 18 14 Inf10 11 0 6 10 19 15 Inf8 5 6 0 4 13 9 Inf12 9 10 4 0 9 5 Inf21 18 19 13 9 0 3 417 14 15 9 5 3 0 6Inf Inf Inf Inf Inf 4 6 0R =1 2 3 2 2 2 2 81 2 4 4 4 4 4 81 4 3 4 4 4 4 82 2345 5 5 84 4 4 4567 85 5 5 5 567 85 5 5 5 567 81 2 3 4 5 6 7 8 k =6D =0 3 10 8 12 21 17 253 0 11 5 9 18 14 2210 11 0 6 10 19 15 238 5 6 0 4 13 9 1712 9 10 4 0 9 5 1321 18 19 13 9 0 3 417 14 15 9 5 3 0 625 22 23 17 13 4 6 0 R =1 2 3 2 2 2 2 21 2 4 4 4 4 4 41 4 3 4 4 4 4 42 2345 5 5 54 4 4 4567 65 5 5 5 567 85 5 5 5 567 86 6 6 6 6 678 k =7D =0 3 10 8 12 20 17 233 0 11 5 9 17 14 2010 11 0 6 10 18 15 218 5 6 0 4 12 9 1512 9 10 4 0 8 5 1120 17 18 12 8 0 3 417 14 15 9 5 3 0 623 20 21 15 11 4 6 0 R =1 2 3 2 2 2 2 21 2 4 4 4 4 4 41 4 3 4 4 4 4 42 2345 5 5 54 4 4 45 7 7 77 7 7 7 7 6 7 85 5 5 5 567 87 7 7 7 7 6 7 8 k =8D =0 3 10 8 12 20 17 233 0 11 5 9 17 14 2010 11 0 6 10 18 15 218 5 6 0 4 12 9 1512 9 10 4 0 8 5 1120 17 18 12 8 0 3 417 14 15 9 5 3 0 623 20 21 15 11 4 6 0R =1 2 3 2 2 2 2 21 2 4 4 4 4 4 41 4 3 4 4 4 4 42 2345 5 5 54 4 4 45 7 7 77 7 7 7 7 6 7 85 5 5 5 567 87 7 7 7 7 6 7 8D =0 3 10 8 12 20 17 233 0 11 5 9 17 14 2010 11 0 6 10 18 15 218 5 6 0 4 12 9 1512 9 10 4 0 8 5 1120 17 18 12 8 0 3 417 14 15 9 5 3 0 623 20 21 15 11 4 6 0 R =1 2 3 2 2 2 2 21 2 4 4 4 4 4 41 4 3 4 4 4 4 42 2345 5 5 54 4 4 45 7 7 77 7 7 7 7 6 7 85 5 5 5 567 87 7 7 7 7 6 7 8四、实验体会。

最短路问题实际案例介绍最短路问题是图论中的一个经典问题,其目标是找到两个顶点之间的最短路径。
这个问题在日常生活中有着广泛的应用,例如导航系统、网络路由以及物流配送等场景中都需要解决最短路问题。
本文将通过实际案例来深入探讨最短路问题及其应用。
什么是最短路问题?最短路问题是指在一个给定的图中,找到两个顶点之间的最短路径。
通常情况下,路径的长度可以通过边的权重来衡量。
最短路问题可以分为单源最短路问题和全源最短路问题,前者是指从一个固定的起点出发,求到图中其他所有顶点的最短路径;后者是指求图中任意两个顶点之间的最短路径。
实际案例:导航系统导航系统是最短路问题的一个典型应用。
当我们使用导航系统来规划路线时,系统需要找到最短路径以优化我们的行车时间。
下面以一个具体案例来说明导航系统如何解决最短路问题。
案例场景假设我们身处一座陌生的城市,想要前往城市中心的一个著名景点。
我们打开导航系统,输入起点和终点信息。
导航系统会根据地图数据自动生成最短路径,并提供导航指引。
导航系统的实现导航系统实现最短路径规划的过程可以分为以下几个步骤:1.构建路网图:将城市中的道路以及交叉口等信息转化为图的形式。
图中的节点表示交叉口,边表示道路,边的权重可以表示行驶距离、时间等。
2.选择算法:根据实际需求选择合适的最短路径算法。
常见的算法有Dijkstra算法、Bellman-Ford算法和A*算法等。
3.计算最短路径:根据选定的算法,在路网图上计算起点到终点的最短路径。
算法会考虑边的权重以及路径的方向等因素。
4.导航指引:根据计算得到的最短路径,导航系统会生成具体的导航指引,包括行驶指示、路口转向、距离和预计时间等信息。
优化策略导航系统通过不断的优化,提高了最短路径的计算效率和准确性。
以下是几种常见的优化策略:1.路网数据更新:导航系统会及时更新路网数据,包括道路信息、交通状况等。
这样可以保证计算得到的最短路径更准确。
2.平行算法:为了加快计算速度,导航系统采用并行算法来计算最短路径。
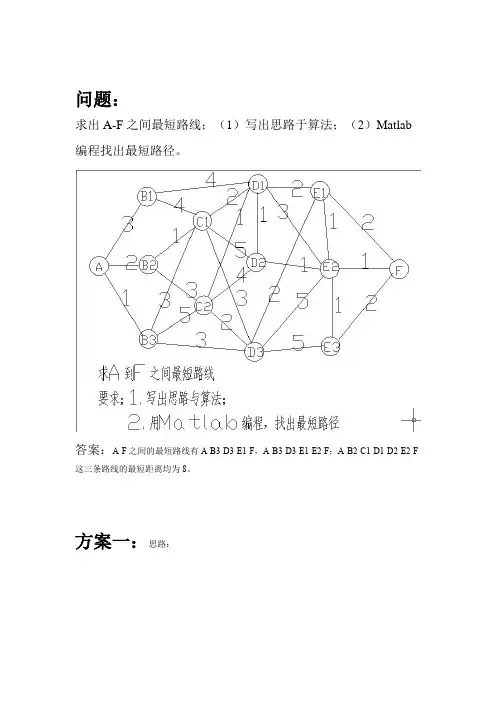
问题:求出A-F之间最短路线;(1)写出思路于算法;(2)Matlab 编程找出最短路径。
答案:A-F之间的最短路线有A-B3-D3-E1-F,A-B3-D3-E1-E2-F;A-B2-C1-D1-D2-E2-F 这三条路线的最短距离均为8。
方案一:思路:对于是否返回的分析:如图可以看出只有B端才能跨越C端的点直接到达D端的,其余的各端点都是必须按照字母顺序一路下来。
若如D端返回到C端或B端这是不可能的,因为这样无疑增加了路程,如图可以看出C端的点能到达D端的各个点,所以要求的直接命中想到达的该点;而D端出发去到E端后有图可以看出不可能再返回D端了,因为这只会增加路线的长度,而且E 端的各点是相通的,也没必要再返回D端;同样B端到达C端或D端的,因为B2,B2到能直接到达C端的各点,只有B1只能到达C1,但B1它到D1的距离和B1点到C1的距离同样为4但也不可能经过C1后返回B端的,因为C1也是联系D端的各点,而且你要返回B 段端,还不如在A端的时候就选择好一个理想的B点,这样距离会更加短。
所以不能进行返回。
如图将我们本来所需要的的路线分成两半,以D字母的为中间端。
后半部分:后半部分主要由D端连接到E端最后才连接到F端的,同时D端无法越过E端直接连接到F端。
更为重要的是前半部分,也必须要经过D端才能与F端相接,所以构成他们之间的枢纽定在D端是最好不过的。
首先的是先分析D端的三个点D1,D2,D3分别到点F的最短距离。
一、已经从D端出发去到E端后有图可以看出不可能再返回D端了,因为这只会增加路线的长度,而且E端的各点是相通的,也没必要再返回D端;二、由图可以看出E端到点F最好的路线是E2-F距离为1,除E2外的E1,E3他们到F点的方式(E1-F, E1-E2-F ,E3-F ,E3-E2-F)的距离均为2;所以如果能先到达E2则可以只考虑E2到F这条路线。
若先到达了E1,或E3、则这路线的最短路径必定变化为两条。

基于最短路问题的研究及应用令狐采学姓名:Fanmeng学号:指导老师:摘要最短路问题是图论中的一大问题,对最短路的研究在数学建模和实际生活中具有很重要的实际意义,介绍最短路问题的定义及这类问题的解决办法Dijkstra算法,并且能够在水渠修建实例运用到此数学建模的方法,为我们解决这类图论问题提供了基本思路与方法。
关键字数学建模最短路问题Dijkstra算法水渠修建。
目录第一章.研究背景1第二章.理论基础22.1 定义22.2 单源最短路问题Dijkstra求解:22.2.1 局限性22.2.2 Dijkstra算法求解步骤22.2.3 时间复杂度22.3 简单样例3第三章.应用实例43.1 题目描述43.2 问题分析43.3符号说明43.4 模型假设53.5模型建立与求解53.5.1模型选用53.5.2模型应用及求解53.6模型评价5第四章. 参考文献5第五章.附录6第一章.研究背景在现实生活中中,我们经常会遇到图类问题,图是一种有顶点和边组成,顶点代表对象,在示意图中我们经常使用点或者原来表示,边表示的是两个对象之间的连接关系,在示意图中,我们使用连接两点G点直接按的下端来表示。
顶点的集合是V,边的集合是E的图记为G[V,E] ,连接两点u和v的边用e(u,v)表示[1]。
最短问题是图论中的基础问题,也是解决图类问题的有效办法之一,在数学建模中会经常遇到,通常会把一个实际问题抽象成一个图,然后来进行求的接任意两点之间的最短距离。
因此掌握最短路问题具有很重要的意义。
第二章.理论基础2.1 定义最短路问题(short-path problem ):若网络中的每条边都有一个数值(长度、成本、时间等),则找出两节点,(通常是源节点和目标节点)之间总权和最小的路径就是最短路问题。
最短路问题是网络理论解决的典型问题之一,可用来解决管道铺设,线路安装,厂区布局和设备更新等实际问题[2]。
2.2 单源最短路问题Dijkstra 求解: 2.2.1局限性Dijkstra 算法不能够处理带有负边的图,即图中任意两点之间的权值必须非负。

基于最短路问题的研究及应用: Fanmeng学号:指导老师:摘要最短路问题是图论中的一大问题,对最短路的研究在数学建模和实际生活中具有很重要的实际意义,介绍最短路问题的定义及这类问题的解决办法Dijkstra算法,并且能够在水渠修建实例运用到此数学建模的方法,为我们解决这类图论问题提供了基本思路与方法。
关键字数学建模最短路问题 Dijkstra算法水渠修建。
目录第一章.研究背景 (1)第二章.理论基础 (2)2.1 定义 (2)2.2 单源最短路问题Dijkstra求解: (2)2.2.1 局限性 (2)2.2.2 Dijkstra算法求解步骤 (2)2.2.3 时间复杂度 (2)2.3 简单样例 (3)第三章.应用实例 (4)3.1 题目描述 (4)3.2 问题分析 (4)3.3符号说明 (5)3.4 模型假设 (5)3.5模型建立与求解 (5)3.5.1模型选用 (5)3.5.2模型应用及求解 (5)3.6模型评价 (5)第四章. 参考文献 (6)第五章.附录 (7)第一章.研究背景在现实生活中中,我们经常会遇到图类问题,图是一种有顶点和边组成,顶点代表对象,在示意图中我们经常使用点或者原来表示,边表示的是两个对象之间的连接关系,在示意图中,我们使用连接两点G点直接按的下端来表示。
顶点的集合是V,边的集合是E的图记为G[V,E] ,连接两点u和v的边用e(u,v)表示[1]。
最短问题是图论中的基础问题,也是解决图类问题的有效办法之一,在数学建模中会经常遇到,通常会把一个实际问题抽象成一个图,然后来进行求的接任意两点之间的最短距离。
因此掌握最短路问题具有很重要的意义。
第二章.理论基础2.1 定义最短路问题(short-path problem ):若网络中的每条边都有一个数值(长度、成本、时间等),则找出两节点,(通常是源节点和目标节点)之间总权和最小的路径就是最短路问题。
最短路问题是网络理论解决的典型问题之一,可用来解决管道铺设,线路安装,厂区布局和设备更新等实际问题[2]。


摘要目前,社区的优化管理和最佳服务已经成为一种趋势,并且为城市的发展作出了一定的贡献。
本文针对在社区中选址问题及巡视路线问题,分别建立了多目标决策模型、约束最优化线路模型,并分别提供了选址社区和巡视路线。
对于问题一,我们建立了单目标优化模型,考虑到各社区居民到收费站点的平均距离最小,我们使用floyd 算法并通过matlab 编程,算出任意两个社区之间的最短路径,并以此作为工具,使用0-1变量列出了目标函数。
在本题中,我们根据收费站数、超额覆盖等确定了约束条件,以保证收费站覆盖每个社区,同时保证居民与最近煤气站之间的平均距离最小,最终利用lingo 软件求得收费站建在M、Q、W三个社区。
对于问题二,同样是单目标优化模型,较之问题一不同的是,问题二不需要考虑人口问题,但需要确定选址的个数。
接下来的工作分了两步,第一步,我们通过0-1变量列出目标函数,以超额覆盖等确定约束条件,用lingo 软件编程求出最小派出所站点的个数;第二步,我们利用第一步中求出的派出所个数作为新的约束条件,建立使总距离最小的优化模型,最终利用lingo 软件求得三个派出所分别建在W、Q、K社区。
对于问题三,我们建立了约束最优化线路模型,根据floyd 算法求得的任意两个社区之间的最短路径,建立了以w 点为树根的最短路径生成树,并据此对各点的集中区域进行划分,再利用破圈法得到最短回路。
在本题中,我们初定了两种方案,并引入均衡度α对两种方案进行比较,最终采用了方案二。
最后,我们用matlab编程求解方案二中各组的巡视路线为113百米,123百米,117百米,均衡度α=8.13%。
具体路线见关键词:最短路径hamilton圈最优化floyd算法0-1变量在社区中缴费站的选址对于居民快速缴费和充分的利用公共设施的资源有很重要的指导意义。
某城市共有24个社区,各社区的人口(单位:千人)如下:(注:横线上的数据表示相邻社区之间的距离,单位:百米)本题要解决的问题如下:(1)方便社区居民缴纳煤气费,煤气公司现拟建三个煤气缴费站,问煤气缴费站为了怎样选址才能使得居民与最近煤气站之间的平均距离最小。