山西省吕梁育星中学2018_2019学年高二数学下学期月考试题(三)(60、61)

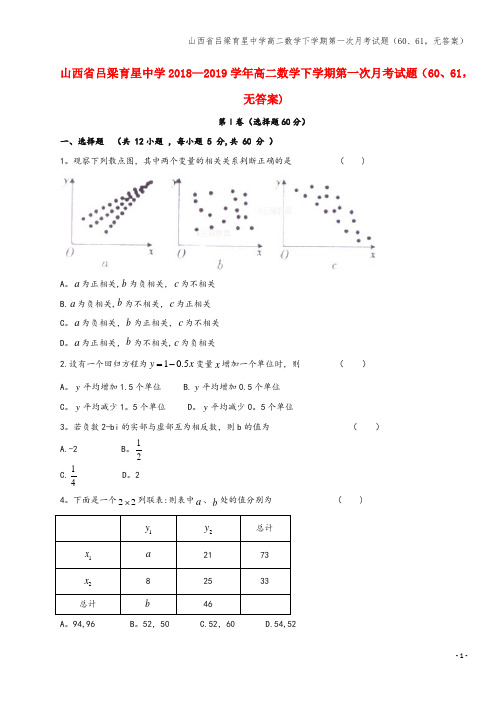
山西省吕梁育星中学2018—2019学年高二数学下学期第一次月考试题（60、61，无答案)第Ⅰ卷（选择题60分）一、选择题 （共 12小题 ，每小题 5 分,共 60 分 ）1。

观察下列散点图，其中两个变量的相关关系判断正确的是 （ )A 。

a 为正相关,b 为负相关，c 为不相关B.a 为负相关,b 为不相关，c 为正相关C 。

a 为负相关，b 为正相关，c 为不相关D 。

a 为正相关，b 为不相关,c 为负相关2.设有一个回归方程为x y 5.01-=变量x 增加一个单位时，则 （ ）A 。

y 平均增加1.5个单位 B.y 平均增加0.5个单位C 。

y 平均减少1。

5个单位D 。

y 平均减少0。

5个单位3。

若负数2-bi 的实部与虚部互为相反数，则b 的值为 （ ）A.-2 B 。

21C.41D 。

24。

下面是一个22⨯列联表:则表中a 、b 处的值分别为 （ ) 1y 2y 总计1x a 21 732x 8 25 33总计 b 46A 。

94,96B 。

52，50 C.52，60 D.54,525. 设,,)22()352(22R t i t t t t z ∈+++-+=下列结论中正确的是 ( ）A.z 在复平面内对应的点在第一象限B. z 一定不是纯虚数C. Z 在复平面内对应的点在实轴上方D. Z 一定是实数6.在对吸烟与患肺病这两个分类变量的计算中，下列说法正确的是 （ ）A 。

若随机变量2k 的观测值635.6>k ，我们有99%的把握说明吸烟与患肺病有关，则若某人吸烟,那么他有99%的可能患有肺病B.若由随机变量求出有99％的把握说吸烟与患肺病有关，则在100个吸烟者中必有99个人患有肺病C 。

若由随机变量求出有95%的把握说吸烟与患肺病有关,那么有5％的可能性使得推断错误D.以上说法均不正确7。

设产品产量与产品质量之间的线性相关系数为0。

97，这说明二者存在着 （ ）A 。

高二下学期第三次月考数学试题文 科说明：本试题考试时间120分钟，满分150分一、选择题：（本大题共12小题，每小题5分，共60分） 1．设全集{}2U x N x =∈≥，集合{}25A x N x =∈≥,则U C A =（ ） A. ∅ B. {}2 C. {}5 D. {}2,52.已知集合{}0,1,2,A =则集合{},B x y x A y A =-∈∈中元素的个数为（ ） A. 1 B. 3 C.5 D.93.已知i 是虚数单位，,a b R ∈,则“1a b ==”是()2"2"a bi i +=的（ ） A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件4.已知2:,:2,p x k q x x ≥->如果p 是q 的充分不必要条件，则实数k 的取值范围为（ ）A. [)1,+∞B. ()2,+∞C. [)2,+∞D. (],1-∞-5.下列命题中正确的是( )A. 若p ∨q 为真命题，则p ∧q 为真命题B. “x ＝5”是“x 2－4x －5＝0”的充分不必要条件C. 命题“若x <－1，则x 2－2x －3>0”的否定为：“若x ≥－1，则x 2－2x －3≤0” D. 已知命题p ：∃x ∈R ，x 2＋x －1<0，则P ⌝： ∃x ∈R ，x 2＋x －1≥06.已知命题:,23;x x P x R ∀∈<命题32:,1q x R x x ∃∈=-，则下列命题为真命题是（） A p q ∧ B p q ⌝∧ C. p q ⌝∧ D. p q ⌝⌝∧ 7.已知()()2'1220152015ln 2f x x xf x =++，则()()'2015f =A.2015B.-2015C.2016D. -20168.参数方程22sin 1cos 2x y θθ⎧=+⎨=-+⎩（θ为参数）化为普通方程为（）.240A x y -+= .240B x y +-=[].240,2,3C x y x -+=∈ [].240,2,3D x y x +-=∈9.在极坐标方程中，曲线C 的方程是ρ＝4sin θ，过点(4，π6)作曲线C 的切线，则切线长为( )A. 4B. 7C. 2 2D. 2 310.观察下列各式：22331,3,4a b a b a b +=+=+=，44557,11,a b a b +=+=L L则()1010a b +=A.28B.76C.123D.19911.已知曲线ln y x =的切线过原点，则此切线的斜率为（ ） A. e B.-e C1e D.-1e12．下图中，有一个是函数f (x )＝13x 3＋ax 2＋(a 2－1)x ＋1(a ∈R ，a ≠0)的导函数f ′(x )的图象，则f (－1)等于( )A.13 B ．－13 C.73 D ．－13或53 二、填空题：（本大题共4小题，每小题5分，共20分） 13.命题[)3"0,,0"x x x ∀∈+∞+>的否定是_____．14.在直角坐标系xoy 中，曲线12,C C 的参数方程分别为55x y θθ⎧=⎪⎨=⎪⎩（θ为参数）和2522x y ⎧=-⎪⎪⎨⎪=⎪⎩（t 为参数）则曲线12,C C 的交点的极坐标______．15..与参数方程为12x ty t⎧=⎪⎨=-⎪⎩ (t 为参数)等价的普通方程是______．16. 若“x 2>1”是“x <a ”的必要不充分条件，则a 的最大值为______． 三、解答题：（本大题共6小题，共70分） 17.（10分）已知集合A ＝{}29x x ≥，B ＝701x x x ⎧-⎫≤⎨⎬+⎩⎭，{}24C x x =-<．（1）求,A B A C ⋂U（2）若U R =，求()U A C B C ⋂⋂18. （12分）已知命题p ：函数()()32xf x a =-是增函数，命题q ：函数y =lg(224x ax ++)的定义域为R ，如果p ∨q 为真命题，p ∧q 为假命题，求实数a 的取值范围．19.（12分）已知曲线C 的极坐标方程是4cos ρθ=，以极点为原点，极轴为x 轴的正半轴建立平面直角坐标系，设直线L 的参数方程为3512x t y t ⎧=+⎪⎪⎨⎪=⎪⎩（t 为参数） （1）求曲线C 的直角坐标方程与直线L 的普通方程 （2）设曲线C 与直线L 相交于P,Q 两点，求PQ20（12分）以直角坐标系的原点O 为极点，X 轴的正半轴为极轴，建立坐标系，两个坐标系取相同的单位长度.已知直线L 的参数方程为1cos sin x t y t aα=+⎧⎨=⎩(t 为参数, 0a π<<),曲线C的极坐标方程为2sin 4cos ρθθ= （1）求曲线C 的直角坐标方程（2）设直线L 与曲线C 相交于A,B 两点,AB =8时，求α的值. 21.在平面直角坐标系xoy 中，已知曲线221:1C x y +=，以直角坐标系的原点O 为极点，X轴的正半轴为极轴，建立坐标系，两个坐标系取相同的单位长度.已知直线():2cos sin 6l ρθθ-=（1）将曲线1C 的所有点的横坐标、纵坐标分别伸长为原来的3、2倍后得到曲线2C ，试写出直线L 的直角坐标方程及曲线2C 的参数方程（2）在曲线2C 上求一点P ，使得点P 到直线L 的距离最大，并求出此最大值 22.已知函数()1ln f x a x x x ⎛⎫=-- ⎪⎝⎭（1）若a =1,求曲线()y f x =在点()(1,1)f 处的切线方程 （2）若函数()f x 在定义域内为增函数，求a 的取值范围.。

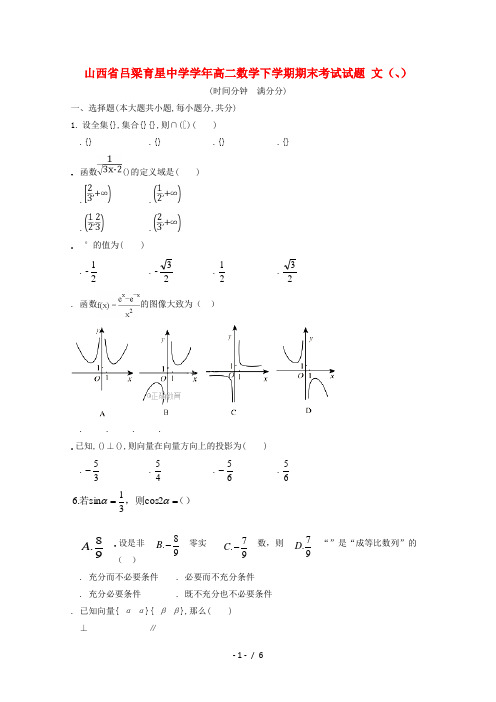
山西省吕梁育星中学学年高二数学下学期期末考试试题 文（、）(时间分钟 满分分)一、选择题(本大题共小题,每小题分,共分)1. 设全集{},集合{}{},则∩(∁)( ) .{}.{} .{} .{} . 函数()的定义域是( ) . . . .. °的值为( ) .21- .23- .21 .23 . 函数的图像大致为（ ）. . . ..已知,()⊥(),则向量在向量方向上的投影为( ) .35- .45 .65- .65 （），则若==αα2cos 31sin .6.设是非零实数，则“”是“成等比数列”的（ ） . 充分而不必要条件 . 必要而不充分条件. 充分必要条件 . 既不充分也不必要条件. 已知向量{ α α}{ β β},那么( )⊥ ∥98.A 98.-B 97.-C 97.D.()⊥() 与的夹角为αβ. 已知等差数列{}的前项和为,若,则( ) .已知向量(), (),若∥,则 等于( ) .65 .54 .17.已知数列{}的前项和为,且对于任意>∈*,满足(),则的值为( ) .在数列{}n a 中,已知()()311++=n n a n (∈*),则{}n a 的前项和 ( ) .312165+-+-n n .⎪⎭⎫ ⎝⎛+-312121n .⎪⎭⎫ ⎝⎛+-+-31113421n n .⎪⎭⎫ ⎝⎛+-+-31216521n n 二、填空题(本大题共小题,每小题分,共分). 曲线在点处的切线方程为． . 已知，则． .x x x sin ),2,0(>∈∀π的否定是.若等差数列{}和等比数列{}满足,则n n b a . 三、解答题(本大题共小题,共分).（分）已知等差数列的前三项依次为,前项和为n S ,且110=k S .()求及的值.()已知数列{}满足nS b n n =,证明数列{}是等差数列,并求其前项和n T . .（分）在△中,内角所对应的边分别为,已知A b B a sin 32sin =. ()求.()若 31,求 的值. .(分)已知,()·(),()求与的夹角θ;()求;()若==,求△的面积..（分）已知数列{}n a 是公差不为的等差数列,首项1a ,且421,,a a a 成等比数列.()求数列{}n a 的通项公式.()设数列{}满足n a n n a b 2+=,求数列{}的前项和为n T . .（分）在△中,角的对边分别为,已知,·△,求和..（分）设函数() (∈).()若,求函数()的单调区间;()若函数()在区间(]上是减函数,求实数的取值范围;高二答案（、数学）一、二、. – . 23 .x x x sin ,2,0≤⎪⎭⎫ ⎝⎛∈∃π 三、.解()设该等差数列为{},则,由已知有,得,公差, 所以·×.由,得, 解得或(舍去),故.()由()得(), 则,故()(),即数列{}是首项为,公差为的等差数列,所以..解()在△中,由可得 ,又由 得 · ,由正弦定理整理得 ,因为为△的内角,所以.()在△中 [π()](),由 得 ,所以 ..解 ()∵()·(), ∴·.又,∴·,∴·.∴ θ又≤θ≤π,∴θ()()· ×(),∴()的夹角θ,∴∠π又,∴△ ∠× .()由题设,得4122a a a ⋅=,即()化简,得又≠,所以,所以.()由()得(…)(…)()22211-+++n n n . .因为·,所以 ,又△,所以 ,因此,又<<π,所以,又,所以,由余弦定理 , 得×××,所以..解 ()时() (>),∴'(),当时'()<;当时'()>.∴()的单调递减区间为,单调递增区间为()解 '()∵()在区间(]上是减函数,∴'()≤对任意∈(]恒成立,即对任意∈(]恒成立.∴对任意∈(]恒成立,令(), ∴≤()易知()在(]上单调递减,∴()().∴≤.。

山西省吕梁育星中学2018-2019学年高二数学上学期第三次月考试题一、选择题（本大题共12小题，每小题5分，共60分）1．下列语句中是命题的是（ )A ．作直线AB B ．x 是整数C ．梯形是四边形D ．今天会下雪吗？2.命题“若A ⊆B ,则A ＝B ”与其逆命题、否命题、逆否命题这四个命题中，真命题的个数是（ ） A ．1 B.2 C 。

3 D.43.“0=θ”是“θsin =0”的（ ）A.充分不必要条件 B 。

必要不充分条件 C.充要条件 D.既不充分也不必要条件4。

若命题q p ∧为假,且p ⌝为假，则（ ）A.p 或q 为假 B 。

q 为假 C 。

p 为假 D 。

不能判断q 的真假5．设集合M ＝{x ｜x >2}，P ＝｛x ｜x 〈3}，那么“x ∈M ,或x ∈P ”是“x ∈M ∩P ”的（ ) A ．必要不充分条件 B ．充分不必要条件 C ．充要条件 D ．既不充分也不必要条件6．已知双曲线12222=-b y a x (a 〉b >0)的离心率为26，椭圆12222=+b y a x 的离心率为（ ）A ．23 B.23C 。

26 D.227。

已知命题1sin ,:≤∈∀x R x p ，则其否定是( ） A 。

1sin ,:00≥∈∃⌝x R x p B.1sin ,:≥∈∀⌝x R x p C 。

1sin ,:00>∈∃⌝x R x p D 。

1sin ,:>∈∀⌝x R x p8.已知命题p:△ABC 中，若A 〉B,则cosA 〉cosB,则下列命题为真命题的是（ ） A 。

p 的逆命题 B.p 的否命题 C 。

p 的逆否命题 D.p 的否定9。

若双曲线的离心率为2,焦点是（-4,0），（4,0),则双曲线的方程为（ ）A 。

112422=-y x B.161022=-y x C 。

141222=-y x D.110622=-y x 10.方程)10(01≤≤=-+x y x 表示的曲线是（ ） A 。

吕梁育星中学2018-2019学年第二学期月考（三）试题高二数学(62)命题时间：2019.06.10（本试卷满分150分，考试时间120分钟）一·选择题（本大题共12个小题，每小题5分，共60分） 1．若218x C -=38x C +，则x 的值为（ ）A ．1或2B ．3或4C ．1或3D ．2或4 2．设是一个离散型随机变量，其分布列为：则等于（ ） A ．1B ．221±223.上海世博会某个展区共有6个展馆,分布在一条直线上,现要在展馆之间安排3名防暴警察,要求相邻的两个展馆之间至多安排一名防暴警察,则不同的安排方法的种数为( ) A.10 B.24 C.32 D.604.随机变量的分布列如下:）1=等于( ) A.61 B.31 C.21 D.325.设盒中有5个球,其中有2个白球, 3个黑球,从中任取3个球, X 表示取到的白球数,则(1)P X =等于( ).A.110 B. 15 C. 310 D. 356.12人的兴趣小组中有5人是“三好学生”,现从中任选6人参加竞赛,若随机变量X 表示参加竞赛的“三好学生”的人数,则6123735C C C 为( ). A. (6)P X = B. (5)P X = C. (3)P X = D. (7)P X =7.旅游体验师小明受某网站邀请,决定对甲、乙、丙、丁这四个景区进行体验式旅游,若甲景区不能最先旅游,乙景区和丁景区不能最后旅游,则小李旅游的方法数为( ) A.24 B.18 C.16 D.108.某地举办科技博览会,有3?个场馆,现将24个志愿者名额分配给这3?个场馆,要求每个场馆至少有一个名额且各场馆名额互不相同的分配方法共有( )种A. 222B. 253C. 276D. 2849.已知nx）（1x -的展开式中第5项与第8项的二项式系数相等,记展开式中系数最大的项为第k 项,则k = ( )A.6B.7C.6或7D.5或6 10、将4名老师分到3个班中去，每班至少一人，共有多少种不同的分法( ) A ．36 B ．72 C ．24 D ．1811.92x⎛- ⎝的展开式中,常数项为( )A.420B.512C.626D.67212.已知随机变量ζ,且ζ服从二项分布()10,0.6?B ,则()E ζ和()D ζ的值分别是( ) A. 6和2.4 B. 2和2.4 C. 2和5.6 D. 6和5.6 二．填空题（本大题共4个小题，每小题5分，共20分）13.一排9个座位坐了3个三口之家.若每家人坐在一起,则不同的坐法种数为 _________. 14.某单位有7个连在一起的车位,现有3辆不同型号的车需停放,如果要求剩余的4个空车位连在一起,则不同的停放方法的种数为___________.15.()()511ax x ++的展开式中2x 的系数是5,则a =__________.16.已知⎰πsin xdx ，则二项式5)-1xa （的展开式中3-x 的系数为____________． 三．解答题（本大题共6个小题，共70分）17.计算1091093102101103327931+-+-+-C C C C .（10分）18.有3本不同的数学书和2本不同的物理书，3本不同的化学书，全部排成一排，若要求数学书互不相邻，同时物理书也互不相邻，有多少种排法 .(结果用数字表示)19.某校随机调查80名学生，以研究学生爱好羽毛球运动与性别的 关系，得到下面的22⨯列联表：将此样本的频率视为总体的概率，随机调查本校的3名学生，设这3人中爱好羽毛 球运动的人数为X ，求X 的分布列和数学期望。

-1 - / 6吕梁育星中学学年第二学期期末试题高二数学(文科、班)(满分分，时间：分钟)一、选择题(本大题共小题，每小题分，共分，在每小题给出的四个选项中，有且只有一项是 符合题意的)「 b 1•若集合 1, —, a = ^0, a b,a 2 '，则 a 2 b^ ().a•若函数y = f (x)的定义域为 M -汉| -2 _ x _ 2f ，值域为 N - \x | 0 _ y _ 2f ，则函数 g x 二 f 2x的定义域是(x —1[,]• [) • [) U (]•()5已知 fgGoXL)，则 3).设全集为，集合={ —V }, = { —VW }，则门(?)=()• ( —, ) •(—,—) •( —,—] •(—,).曲线的直角坐标方程为 x 2 • y 2-2x=0，以原点为极点，x 轴的正半轴为极轴建立极坐标系, 则曲线的极坐标方程为()F 列各组函数表示同一函数的是( f X = X 2 , g X =■x).f x =1, g x = x 0f x =3 X 2 ,g X = 3 xf x =x 1 ,g x =x 2 -1 x — 1y =f(x)的图象可能是() .若函数y = f x 的定义域为[],则函数：? - 2sin n ：? =cosn2（本小题满分分）-2 - / 6• Q = 2cosv.若偶函数f （x ）在（0,：：）上是减函数, 则下列关系式中成立的是12 3• f(—) f(- —) f(—)3 4 1、 .22•宦煜©1 3 2• f( ) f( ) ■ f()2 422 •弋）飞）•函数f(x) = — + ,€ []的值域是• [ —,+m)1函数（）- （）X —1在（-,m）上单调递增 在（，s ）上单调递增 在（-,m）上单调递减在（，^）上单调递减若函数y =a （x 3 -x ）的单调递减区间为，则a 的取值范围是I3 3丿a > 0-1 v a v 0a > 10 v a v 112.已知直线 l 的参数方程为（为参数），• -1厂2二、填空题（本大题共个小题，每小题分，共分 .函数f （x ）=的定义域是• .设集合｛,•已知函数 f X 1 = x 2 -1 ,则 f (x) •.如果函数 g(x )= “ '2x-3, (x 〉0) L f (x)(x £0)是奇函数，则•(分)：? - 2sin n ：? =cosn3三.解答题：解答应写出文字说明，证明过程或演算步骤（本小题满分分）-3 - / 6-4 - / 691,设函数f (x)的定义域为集合 A ，已知集合 B = lx |3 ：：： 2x • 1 ：：：7 ,C - (x | x _ m},全集为 R .()求(C R A)PI B ； ()若AUB Re = ,求实数m 的取值范围.18. (本小题满分分)()求函数y x~3x _4的定义域In (x+1 )x 2 — X +1()求f X的值域x19. (本小题满分分)以轴的正半轴为极轴，建立极坐标系，曲线的极坐标方程为()写出的普通方程和的直角坐标方程；()设点在上，点在上，求的最小值及此时的直角坐标 (本小题满分分)ax 2 +2已知函数f x = ax是奇函数，且3x+b()求实数a,b 的值；f2i .()求函数f x 的单调区间.(本小题满分分)在直角坐标系xoy 中，曲线的参数方程为 x =V3 cos ay = si n 。

2018年山西省吕梁市育星中学高二数学文月考试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 椭圆的左、右顶点分别为，点在上且直线的斜率的取值范围是，那么直线斜率的取值范围是（）A．B．C．D．参考答案：B略2. 函数的图像关于直线对称的充要条件是（）A. B. C.D.参考答案：A略3. 已知向量，，若向量满足，，则向量( )A. B. C. D.参考答案：A4. 若直线=1与图x2+y2=1有公共点，则( )A．a2+b2≤1B．a2+b2≥1C．D．参考答案：D【考点】直线与圆的位置关系．【分析】用圆心到直线的距离小于或等于半径，可以得到结果．【解答】解：直线与圆有公共点，即直线与圆相切或相交得：d≤r故选D．【点评】本题考查点到直线的距离公式，直线和圆的位置关系，是基础题．5. 已知双曲线：（）的离心率为，则的渐近线方程为A. B. C. D.参考答案：C略6. 从不同号码的双鞋中任取只，其中恰好有双的取法种数为（）A． B． C． D．参考答案：A略7. 若复数,则（）A．B． C． D．参考答案：B8. 函数f（x）=﹣ln（x﹣1）的零点所在的大致区间为（）A．（1，2）B．（2，3）C．（3，4）D．（1，2）与（2，3）参考答案：B【考点】二分法求方程的近似解．【分析】根据所给的几个区间看出不在定义域中的区间去掉，把所给的区间的两个端点的函数值求出，若一个区间对应的函数值符号相反，得到结果．【解答】解：因为x＞0时，﹣ln（x+1）和都是减函数所以f（x）在x＞1是减函数，所有最多一个零点，f（2）=1﹣ln1＞0，f（3）=﹣ln2==，因为=2≈2.828，所以＞e，故lne＜ln，即1＜ln，所以2＜ln8，所以f（2）f（3）＜0所以函数的零点在（2，3）之间．故选：B．9. 圆上的点到直线的距离最大值是A B C D参考答案：B10. 已知随机变量服从正态分布，，则（）A. 0.89B. 0.22C. 0.11D. 0.78参考答案：C【分析】由随机变量服从正态分布，可得这组数据对应的正态曲线的对称轴，利用正态曲线的对称性，即可得到结论.【详解】随机变量服从正态分布，这组数据对应的正态曲线的对称轴，，，，，故选C.【点睛】本题主要考查正态分布的性质，属于中档题.有关正态分布应用的题考查知识点较为清晰，只要熟练掌握正态分布的性质，特别是状态曲线的对称性以及各个区间概率之间的关系，问题就能迎刃而解.二、填空题:本大题共7小题,每小题4分,共28分11. 从一块短轴长为的椭圆形玻璃镜中划出一块面积最大的矩形，其面积的取值范围是，则该椭圆离心率的取值范围是．参考答案：略12. (理)若曲线在点处的切线与两个坐标围成的三角形的面积为18,则a= .参考答案：64略13. 直线x+2y=0被曲线x2+y2－6x－2y－15=0所截得的弦长等于____________.参考答案：14. 已知A（1，－2，11）、B（4，2，3）、C（x，y，15）三点共线，则x y=___________。

山西省吕梁育星中学2017-2018学年高二数学下学期期末考试试题 文（51、52）(时间:120分钟 满分:150分)一、选择题(本大题共12小题,每小题5分,共60分)1. 设全集U={1,2,3,4,5},集合A={1,2},B={x|x 2-5x+6=0},则A ∩(∁U B )=( ) A.{4,5} B.{2,3}C.{1}D.{4}2. 函数y=+lg(2x-1)的定义域是( )A .B .C .D .3. sin 600°的值为( )A.21-B.23-C.21 D.23 4. 函数的图像大致为（ ）A. AB. BC. CD. D5.已知|a |=2,|b |=3,(2a +b )⊥(a -2b ),则向量b 在向量a 方向上的投影为( )A.35-B.45 C.65-D.65 （），则若==αα2cos 31sin .67.设a,b,c,d 是非零实数，则“ad=bc ”是“a,b,c,d 成等比数列”的（ ） A. 充分而不必要条件 B. 必要而不充分条件 C. 充分必要条件 D. 既不充分也不必要条件8. 已知向量a ={cos α,sin α},b ={cos β,sin β},那么( ) A.a ⊥bB.a ∥bC.(a +b )⊥(a -b )D.a 与b 的夹角为α+β9. 已知等差数列{a n }的前n 项和为S n ,若S 3=9,S 5=25,则S 7= ( ) A.41B.48C.49D.5610.已知向量a =(1,2), b =(-2,m),若a ∥b ,则|2a +3 b |等于( ) A.65 B.54 C.17 D.8011.已知数列{a n }的前n 项和为S n ,a 1=1,a 2=2,且对于任意n>1,n ∈N *,满足S n+1+S n-1=2(S n +1),则S 10的值为( ) A.91B.90C.55D.5412.在数列{}n a 中,已知()()311++=n n a n (n ∈N *),则{}n a 的前n 项和S n = ( )A.312165+-+-n n B.⎪⎭⎫ ⎝⎛+-312121n C.⎪⎭⎫⎝⎛+-+-31113421n nD.⎪⎭⎫⎝⎛+-+-31216521n n二、填空题(本大题共4小题,每小题5分,共20分) 13. 曲线在点处的切线方程为__________．98.A 98.-B 97.-C 97.D14. 已知，则_________．15.x x x sin ),2,0(>∈∀π的否定是16.若等差数列{a n }和等比数列{b n }满足a 1=b 1=-1,a 4=b 4=8,则nnb a =______. 三、解答题(本大题共6小题,共70分)17.（10分）已知等差数列的前三项依次为a,4,3a,前n 项和为n S ,且110=k S .(1)求a 及k 的值. (2)已知数列{b n }满足nS b nn =,证明数列{b n }是等差数列,并求其前n 项和n T . 18.（12分）在△ABC 中,内角A,B,C 所对应的边分别为a,b,c,已知A b B a sin 32sin =.(1)求B.(2)若cos A=31,求sin C 的值.19.(12分)已知|a |=4,|b |=3,(2a -3b )·(2a +b )=61,(1)求a 与b 的夹角θ; (2)求|a +b |;(3)若=AB a,=b,求△ABC 的面积.20.（12分）已知数列{}n a 是公差不为0的等差数列,首项1a =1,且421,,a a a 成等比数列.(1)求数列{}n a 的通项公式.(2)设数列{b n }满足n a n n a b 2+=,求数列{b n }的前n 项和为n T . 21.（12分）在△ABC 中,角A,B,C 的对边分别为a,b,c,已知b=3,·=-6,S △ABC =3,求A 和a.22.（12分）设函数f (x )=x 2+ax-ln x (a ∈R ).(1)若a=1,求函数f (x )的单调区间;(2)若函数f (x )在区间(0,1]上是减函数,求实数a 的取值范围;高二答案（51、52数学） 一、1~6 CDBBAD 7~12 BCCBAD二、13. y =2x –2 14. 2315.x x x sin ,2,0≤⎪⎭⎫⎝⎛∈∃π 16.1三、17.解(1)设该等差数列为{a n },则a 1=a,a 2=4,a 3=3a,由已知有a+3a=8,得a 1=a=2,公差d=4-2=2,所以S k =ka 1+·d=2k+×2=k 2+k.由S k =110,得k 2+k-110=0,解得k=10或k=-11(舍去),故a=2,k=10.(2)由(1)得S n ==n(n+1),则b n ==n+1,故b n+1-b n =(n+2)-(n+1)=1,即数列{b n }是首项为2,公差为1的等差数列,所以T n ==.18.解(1)在△ABC 中,由=可得asin B=bsin A,又由asin 2B=bsin A 得2asin B ·cos B=bsin A,由正弦定理整理得cos B=,因为B 为△ABC 的内角,所以B=. (2)在△ABC 中,sin C=sin[π-(A+B)]=sin(A+B),由cos A=得sin A=,所以sin C=sin =sin A+cos A=.19.解 (1)∵(2a-3b )·(2a+b )=61,∴4|a|2-4a ·b-3|b|2=61.又|a|=4,|b|=3,∴64-4a ·b-27=61,∴a ·b =-6.∴cos θ==-又0≤θ≤π,∴θ=(2)|a+b|2=(a+b )2=|a|2+2a ·b+|b|2=42+2×(-6)+32=13,∴|a+b|=(3)的夹角θ=,∴∠ABC=π-又||=|a |=4,||=|b |=3,∴S △ABC =|||sin ∠ABC=4×3=320.(1)由题设,得4122a a a ⋅=,即(1+d)2=1+3d 化简,得d 2-d=0 又d ≠0,所以d=1,所以a n =n. (2)由(1)得,b n =n+2nT n =(1+2+3+…+n)+(2+22+…+2n )=()22211-+++n n n . 21.因为·=-6,所以bccos A=-6,又S △ABC =3,所以bcsin A=6,因此tan A=-1,又0<A<π,所以A=,又b=3,所以c=2,由余弦定理a 2=b 2+c 2-2bccos A,得a 2=9+8-2×3×2×=29,所以a=.22.解 (1)a=1时,f (x )=x 2+x-ln x (x>0),∴f'(x )()()x x x x x 112112+-=-+=,当⎪⎭⎫ ⎝⎛∈2,0πx 时,f'(x )<0;当⎪⎭⎫⎝⎛+∞∈,21x 时,f'(x )>0.∴f (x )的单调递减区间为,单调递增区间为(2)解 f'(x )=xa x 12-+∵f (x )在区间(0,1]上是减函数,∴f'(x )≤0对任意x ∈(0,1]恒成立,即012≤-+xa x 对任意x ∈(0,1]恒成立.∴x x a 21-≤对任意x ∈(0,1]恒成立,令g (x )=x x21-,∴a ≤g (x )min易知g (x )在(0,1]上单调递减,∴g (x )min =g (1)=-1.∴a ≤-1.。

第三章 一元一次方程 3.1 从算式到方程 3.1.1一元一 次方程（1） 创设情境，回顾概念 1.“猜一猜我的年龄” 我是11月出生的，我年龄的2倍加上6，正好是我出生的那个月总天数的2倍，请你们猜一猜我的年龄是多少岁？ 你能举出一些方程的例子吗？ 含有未知数的等式——方程 创设情境，回顾概念 2.“日历中的数学” 游戏：请同学们圈出日历中一个竖列上相邻的三个日期，把它们的和告诉老师，老师能马上知道这三天分别是几号.请同学们想想老师是如何得到答案的. 问题 你能比较一下算术方法和方程解决问题的不同之处吗？算术方法解决问题时在列算式时只能用已知数；而方程是根据问题中数量关系列出的等式，其中既含有已知数，又含有用字母表示的未知数． 方程小史 “方程”一词来源于我国古算书《九章算术》.在这部著作中，已经会列一元一次方程. 宋元时期，中国数学家创立了“天元术”，用天元表示未知数进而建立方程.这种方法的代表作是数学家李冶写的《测圆海镜》书中所说的“立天元一”相当于现在的“设未知数x”. 清代数学家李善兰翻译外国数学著作时，开始将equation一词译为“方程”，至今一直这样沿用. 问题 一辆客车和一辆卡车同时从 A地出发沿同一公路同方向行驶，客车的行驶速度是70 km/h，卡车的行驶速度是60 km/h，客车比卡车早1 h经过B地.A，B两地间的路程是多少？ 回顾:路程=速度×时间 速度=路程÷时间 时间=路程÷速度 合作交流，探究新知 分析：如果设A，B两地相距 x km， 因为客车比卡车早1 h 经过B 地，所以___ 比 ____小1． 客车从A地到B地的行驶时间为______h, 卡车从A地到B地的行驶时间为_______h． 用含 x的式子表示关于时间的数量： 例1：根据下列问题，设未知数并列出方程： (1) 一台计算机已使用1 700小时，预计每月再使用150小时，经过多少月这台计算机的使用时间达到规定的修检时间2 450小时？ (2) 某校女生占全体学生的52%，比男生 多80人，这个学校有多少学生？ （3）足球的表面是由若干黑色五边形和白色六边形皮块围成的，黑、白皮块数目比为3:5，一个足球的表面一共32块皮块，你能说出黑色皮块和白色皮块各有多少吗？ 归纳： 实际问题 一元一次方程 设未知数 找等量关系 方程只含有一个未知数(元)，未知数的次数都是1的方程叫做一元一次方程. 练习1：判断下列式子是方程吗？如果是，哪些又是一元一次方程呢，为什么？ (1) 2x+1 (2) 2m+15=3 (3) 3x-5=5x+4 (4) x2+2x-6=0 (5) -3x+1.8=3y (6) 3a+9>15 概念辨析，巩固延伸 方程有_________； 一元一次方程有__________． (2)(3)(4)(5) (2)(3) 上有20头， 下有52足，问鸡兔各有多少？ 练习2： 练习3：任选下列方程其中之一，分组设计一道有实际背景的应用题． (1) 3x-5=2x+4 (2)2(x+5x)=120 (3) 小 结 本节课你有哪些收获？ 课堂小结，布置作业 作业：。

山西省吕梁育星中学高二数学下学期第一次月考试题575859无答案一、选择题(本大题共12小题，每小题5分，共60分)1.下列集合中表示同一集合的是( )A.M={(3,2)},N={(2,3)}B.M={2,3},N={3,2}C.M={(x ,y )|x+y=1},N={y|x+y=1}D.M={2,3},N={(2,3)}2.若集合A={x|-2<x<1},B={x|x<-1或x>3},则A ∩B= ( )A.{x|-2<x<-1}B.{x|-2<x<3}C.{x|-1<x<1}D.{x|1<x<3}3.命题“若3πα=,则23sin =α”的逆否命题是( )A.若3πα≠,则23sin =α B.若3πα=,则23sin ≠αC.若23sin ≠α,则3πα≠ D.若23sin ≠α,则3πα=4已知集合A={x||x-2|≤1},且A ∩B=φ,则集合B 可能是( )A.{2,5}B.{x|x 2≤1}C.(1,2)D.(-∞,-1)5.幂函数34x y =的图像是（ ）6.如果0,0≥≥y x ，且12=+y x ，那么232y x +的最小值为 （ ）A. 2B. 34C. 23D. 07.给出4个幂函数的图象，则与图象对应的函数解析式大致是( )A ．①31x y =，②2x y =，③21x y =，④1-=x yB ．①3x y =，②2x y =，③21x y =，④1-=x yC ．①2x y =，②3x y =，③21x y =，④1-=x yD ．①31x y =，②21x y =，③2x y =，④1-=x y8．已知函数c bx ax y ++=2，如果c b a >>且0=++c b a ，则它的图象可能是( )9.已知集合{}{}2|,|<=<=x x B a x x A ，且R B C A R =)( ，则a 满足 ( ) A ．a ≥2 B ．a ＞2C ．a ＜2D ．a ≤210.若定义在R 上的二次函数b ax ax x f +-=4)(2在区间[0,2]上是增函数，且f(m)≥f(0)，则实数m 的取值范围是( )A ．0≤m ≤4B ．0≤m ≤2C ．m ≤0D ．m ≤0或m ≥4 11.已知条件p ：|x+1|＞2，条件q ： 265x x >-，p ⌝则是q ⌝的（ ）A 、充分必要条件B 、充分非必要条件C 、必要非充分条件D 、既非充分又非必要条件12.已知集合A={1,2,3,4,5},B={(x ,y )|x ∈A ,y ∈A ,x-y ∈A },则B 中所含元素的个数为( )A.3B.6C.8D.10二、填空题(本大题共4小题，每小题5分，共20分)13..已知集合A={x|4≤2x≤16},B=[a ,b ],若A ⊆B ,则实数a-b 的取值范围是14.已知集合A={x|-2≤x ≤7},B={x|m+1<x<2m-1},若B ⊆A ,则实数m 的取值范围是 .15.若二次函数c bx ax y ++=2的图象与x 轴交于A(－2,0)，B(4,0)且函数的最大值为9，则这个二次函数的表达式是________．16.已知函数52)(2+-=ax x x f 在(－∞，2]上是减函数，且对任意的21,x x ∈[1，a ＋1]，总有|)()(21x f x f -|≤4，则实数a 的取值范围是________．三、解答题(本大题共6小题，共70分)17.已知二次函数)(x f 的二次项系数为a ，且)(x f ＞x 2-的解集为{x |1＜x ＜3}，方程06)(=+a x f 有两个相等的实根，求)(x f 的解析式.18.已知二次函数bx ax x f +=2)(（b a ,为常数，且0≠a ），满足条件)1()1(x f x f -=+，且方程x x f =)(有相等的实根.（1）求f （x ）的解析式；（2）是否存在实数m ，n （m ＜n ），使f （x ）的定义域和值域分别为[m ，n]和[3m ，3n]？如果存在，求出m ，n 的值；如果不存在，请说明理由.19.若二次函数)0()(2≠++=a c bx ax x f 满足x x f x f 2)()1(=-+，且1)0(=f .(1)求函数)(x f 的解析式；(2)若在区间[－1,1]上，不等式m x x f +>2)(恒成立，求实数m 的取值范围．20.设全集U={x x *,5N x ∈≤且},集合A={x 052=+-q x x },B={x0122=++px x },且=B A C U )({1，4，3，5}，求实数q p ,的值.21.写出命题“若0872=-+x x ,则x=-8或x=1”的逆命题、否命题、逆否命题 ,并分别判断它们的真假.22. 已知集合S ＝{3,2，322-+a a }，A ＝{|a ＋1|，2}，=A C S {3+a }，求a 的值．。