人教A版数学选修33 球面上的几何第六讲第二节多面体欧拉定理的发现与简单应用
- 格式:pptx
- 大小:1.10 MB
- 文档页数:14



人教A版选修3《用球面多边形的内角和公式证明欧拉公式》教案及教学反思教学目标•了解欧拉公式在几何学上的应用;•掌握球面多边形的内角和公式,理解其推导过程;•能够应用所学知识证明欧拉公式。
教学内容1.欧拉公式在几何学上的应用–介绍欧拉公式的定义和公式形式;–理解欧拉公式在不同领域中的应用,如物理学、数学等。
2.球面多边形的内角和公式–定义球面多边形,介绍其特性;–推导球面多边形的内角和公式;–应用球面多边形的内角和公式实际解题。
3.用球面多边形的内角和公式证明欧拉公式–根据定义和推导过程,将球面多边形的内角和公式代入欧拉公式中;–证明欧拉公式在球面多边形中成立。
教学步骤1.欧拉公式在几何学上的应用–导入:师生交流,了解欧拉公式的定义和公式形式;–讲解:介绍欧拉公式在不同领域中的应用;–拓展:让学生思考欧拉公式在实际生活中的应用。
2.球面多边形的内角和公式–导入:通过讨论地球表面的两点间最短距离,引出球面多边形的概念;–讲解:介绍球面多边形的定义、特性以及内角和公式的推导过程;–演示:通过画图演示球面多边形的内角和计算过程;–练习:让学生自行计算球面多边形的内角和。
3.用球面多边形的内角和公式证明欧拉公式–讲解:根据定义和推导过程,将球面多边形的内角和公式代入欧拉公式中;–演示:通过实例演示如何用球面多边形的内角和公式证明欧拉公式;–练习:让学生自行用球面多边形的内角和公式证明欧拉公式。
4.总结反思–总结:师生共同总结所学知识;–反思:学生反思自己在学习过程中存在的不足,师生共同找出解决方法。
教学评估及作业1.教学评估:通过课堂小测验、问题解答等形式进行评估;2.作业:要求学生自行寻找并整理出欧拉公式的不同应用案例,并给出相应的图表或计算结果。
教学心得及教学反思本堂课的教学目标是让学生了解欧拉公式在几何学上的应用,掌握球面多边形的内角和公式,能够应用所学知识证明欧拉公式。
整堂课的教学内容设计合理,步骤清晰,学生也积极参与了课堂活动。



人教版高中选修3-3二简单多面体的欧拉公式教学设计一、教学目标1.理解欧拉公式的含义和应用;2.掌握二简单多面体的定义、性质和分类方法;3.能够通过欧拉公式计算二简单多面体的顶点数、边数和面数。
二、教学准备1.教师备课素材:黑板、白板、彩色粉笔、多面体模型、PPT课件等;2.学生教学素材:笔、本、尺子、计算器等。
三、教学过程1. 导入环节通过一些引人入胜的例子引起学生对多面体的兴趣,比如:1.将一些多面体模型随机散布在教室中,请学生找出其中的二简单多面体;2.让学生观察类似于足球、篮球等多面体形状的物体,引导学生思考此类物体有哪些共同特征。
2. 正式教学2.1 多面体的定义和性质1.定义:边界为多面体中一些平面图形的空间集合。
2.性质:任意两个面不重合,任何面的两个相邻面不在同一平面,多面体中的任意一点都在某一个面的内部或边界上。
2.2 二简单多面体的分类1.棱柱:底面为任意多边形,侧面为平行四边形。
2.棱锥:底面为任意多边形,侧面为三角形。
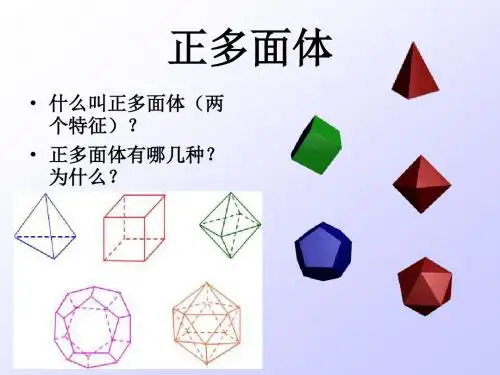
3.正四面体:4个全等的等边三角形所构成的多面体。
4.正六面体:6个全等的正方形所构成的多面体。
5.正八面体:8个全等的等边三角形所构成的多面体。
6.正十二面体:12个全等的正五边形所构成的多面体。
7.正二十面体:20个全等的正三角形所构成的多面体。
2.3 欧拉公式的定义和应用1.定义:对于任意一个简单多面体,其顶点数、边数和面数满足以下公式:V−E+F=2。
2.应用:通过欧拉公式,可以计算一个多面体的未知数量。
比如已知二简单多面体的某两个数量,就可以通过欧拉公式求出另一个未知量。
3. 实例演练3.1 计算正八面体的顶点数、边数和面数1.首先,定义正八面体的数量:V表示顶点数,E表示边数,F表示面数;2.根据正八面体的定义,有:$V=6\\cdot 8/2=24$,$E=3\\cdot 8=24$,F=8;3.将数值带入欧拉公式得:24−24+8=2,等号右侧为2。


【课 题】研究性课题:多面体欧拉公式的发现(2)【教学目标】要求掌握用欧拉公式解决实际问题,特别是用来证明正多面体有且只有五种这一结论。
【教学重点】欧拉公式的应用.【教学难点】【教学过程】一、 复习引入1.简单多面体:考虑一个多面体,例如正六面体,假定它的面是用橡胶薄膜做成的,如果充以气体,那么它就会连续(不破裂)变形,最后可变为一个球面过连续变形可变为球面的多面体,叫做简单多面体3.欧拉定理(欧拉公式):简单多面体的顶点数V 、面数F 及棱数E 有关系式: 2V F E +-=.二、 讲解新课【例1】 由欧拉定理证明:正多面体只有正四面体、正六面体、正八面体、正十二面体、正二十面体这五种。
证明:设正多面体的每个面的边数为n ,每个顶点连有m 条棱,令这个多面体的面数为F ,每个面有n 条边,故共有nF 条边,由于每条边都是两个面的公共边,故多面体棱数2nF E = (1) 令这个多面体有V 个顶点,每一个顶点处有m 条棱,故共有mV 条棱。
由于每条棱有两个顶点,故多面体棱数2mV E =(2) 由(1)(2)得:2E F n =,2E V m =代入欧拉公式:222E E E m n+-=. ∴11112m n E +-= (3), ∵又3m ≥,3n ≥,但m ,n 不能同时大于3,否则,若3m >,3n >,则有11102m n +-≤,即10E≤这是不可能的。
∴m ,n 中至少有一个等于3.令3n =,则1111032m E +-=>,∴116m >,∴5m ≤,∴35m ≤≤. 同样若3m =可得35n ≤≤.【例2】 欧拉定理在研究化学分子结构中的应用:1996年诺贝尔化学奖授予对发现60C 有重大贡献的三位科学家60是由60个C 原子构成的分子,它是形如足球的多面体。
这个多面体有60个顶点,以每一个顶点为一端点都有三条棱,面的形状只有五边形和六边形,计算60C 分子中五边形和六边形的数目解:设C 60分子中形状为五边形和六边形的面各有x 个和y 个.多面体的顶点数V =60,面数F =x +y ,棱数E =21(3×60),根据欧拉公式,可得 60+(x +y )-21(3×60)=2 另一方面,棱数也可由多边形的边数来表示,即21(5x +6y )=21(3×60) 由以上两方程可解得:x =12,y =20答:C 60分子中形状为五边形和六边形的面各有12个和60个.【例3】 一个正多面体各个面的内角和为20π,求它的面数、顶点数和棱数解:由题意设每一个面的边数为m ,则(2)20F m ππ-=,∴(2)20F m -=, ∵2mF E =,∴10E F =+, 将其代入欧拉公式2V F E +-=,得12V =,设过每一个顶点的棱数为n , 则62n E V n ==,12n F m =得121262n n m +-=,即5213n m +=(1), ∵3m ≥,∴5n ≤,又3n ≥,∴n 的可能取值为3,4,5,当3n =或4n =时(1)中m 无整数解;当5n =,由(1)得3m =,∴30E =, ∴20F =,综上可知:30E =,12V =,20F =.【例4】 有没有棱数是7的简单多面体?具体说明理由。