5.2平面直角坐标系(1)学案(新)

6.1平面直角坐标系金乡二中金满拉认知目标：1、认识并能画出平面直角坐标系；能在方格纸上建立适当的直角坐标系。

2、初步理解坐标平面内点与有序实数对的一一对应关系，并能熟练地由点的位置求坐标；明确数轴上点的数据特征和四个象限中的点的符号特征。

能力目标：渗透数形结合、转化的数学思想；揭示人类认识世界是由特殊到一般、具体到抽象、一维到多维等认识规律，发展学生的数形结合意识、合作交流意识，培养学生的发散思维能力和创新能力。

情感目标：培养学生细致、认真的学习习惯。

通过介绍笛卡尔创立直角坐标系的背景知识，激励学生敢于探索，勇攀科学高峰。

教学重点：由点求坐标及（a,b）,(b,a)的区别和书写顺序。

教学难点：坐标平面内的点与有序实数对的一一对应关系。

教学方法：探索式教学法，引导学生从已有的知识和生活经验出发，提出问题与学生共同探索，讨论解决问题的方法。

教学准备：三角板、坐标纸和小黑板。

教学过程：一、引入新课1、什么是数轴？(规定了原点，正方向及长度单位的直线)2、数轴上的点与实数间的关系是什么？(一一对应关系，即数轴上每一个点的位置都能用一个实数表示，反之，任何一个实数在数轴上都有唯一的一个点和它对应，这个实数叫做这个点在数轴上的坐标).例如，P121数轴上的点A，O，B对应的数分别是4，0，-2；4，0，-2分别是点A，O，B的坐标。

数轴上的点的位置可用坐标来确定。

（图略）完成P122练习3、在电影院里怎样确定一个观众的位置？（互相讨论后回答）4、在现实生活中这样的例子很多，你们能不能举出一些现实生活中用一对实数来表示平面内点的位置的例子呢？(小组讨论，全班交流)5、提出问题：究竟如何用一对实数来表示平面内的点的位置呢？接下来介绍笛卡尔的平面直角坐标系。

早在1637年以前，法国数学家、解析几何的创始人笛卡尔受到了经纬度的启发，地理上的经纬度是以赤道和本初子午线为标准的，这两条线从局部上可以看成是平面内互相垂直的两条直线。

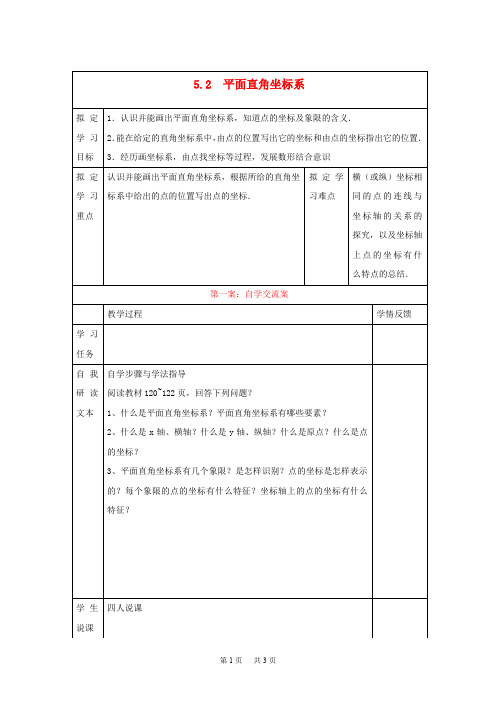
第三章 位置与坐标3. 2 平面直角坐标系 第 1 课时 教学设计《平面直角坐标系》是八年级上册第五章《位置与坐标》第二节内容.本章是“图形与坐标”的主体内容，不仅呈现了“确定位置的多种方法、平面直角坐标系”等内容，而且也从坐标的角度使学生进一步体会图形平移、轴对称的数学内涵，同时又是一次函数的重要基础.《平面直角坐标系》反映平面直角坐标系与现实世界的密切联系，让学生认识数学与人类生活的密切联系和对人类历史发展的作用，提高学生参加数学学习活动的积极性和好奇心.因此，教学过程中创设生动活泼、直观形象、且贴近他们生活的问题情境，会引起学生的极大关注，会有利于学生对内容的较深层次的理解；另一方面，学生已经具备了一定的学习能力，可多为学生创造自主学习、合作交流的机会，促使他们主动参与、积极探究. 1. 理解平面直角坐标系以及横轴、纵轴、原点、坐标等概念；认识并能画出平面直角坐标系；能在给定的直角坐标系中，由点的位置写出它的坐标.2. 通过画坐标系、由点找坐标等过程，发展学生的数形结合意识、合作交流意识；通过对一些点的坐标进行观察，探索坐标轴上点的坐标有什么特点，纵坐标或横坐标相同的点所连成的线段与两坐标轴之间的关系，培养学生的探索意识和能力.3. 由平面直角坐标系的有关内容，以及由点找坐标，反映平面直角坐标系与现实世界的密切联系，让学生认识数学与人类生活的密切联系和对人类历史发展的作用，提高学生参加数学学习活动的积极性和好奇心.【教学重点】1．理解平面直角坐标系的有关知识；2．在给定的平面直角坐标系中，会根据点的位置写出它的坐标；3．由观察点的坐标、纵坐标或横坐标相同的点所连成的线段与两坐标轴之间的关系，说明坐标轴上点的坐标有什么特点.【教学难点】1．横（或纵）坐标相同的点的连线与坐标轴的关系的探究；2．坐标轴上点的坐标有什么特点的总结.◆课前准备◆学生每人准备好草稿纸、铅笔、直尺；教师准备课件，图片，三角板.◆教学过程一、创设情境，引入新知同学们，你们喜欢旅游吗？假如你到了某一个城市旅游，那么你应怎样确定旅游景点的位置呢？下面给出一张某市旅游景点的示意图，根据示意图（图5－6），回答以下问题：（1）你是怎样确定各个景点位置的？（2）“大成殿”在“中心广场”南、西各多少个格？“碑林”在“中心广场”北、东各多少个格？（3）如果以“中心广场”为原点作两条互相垂直的数轴，分别取向右、向上的方向为数轴的正方向，一个方格的边长看做一个单位长度，那么你能表示“碑林”的位置吗？“大成殿”的位置呢？在上一节课，我们已经学习了许多确定位置的方法，这个问题中，大家看用哪种方法比较合适？二、合作交流，探究新知1. 小红在旅游示意图上画上了方格，标上数字，并用（0，0）表示科技大学的位置，用（5，7）表示中心广场的位置，那么钟楼的位置如何表示？（2，5）表示哪个地点的位置？（5，2）？2.如果小亮和他的朋友在中心广场，并以中心广场为“原点”，做了如图所示的标记，那么你能表示“碑林”的位置吗？“大成殿”的位置呢？概念学习在平面内，两条互相垂直且有公共原点的数轴组成平面直角坐标系，如图所示.水平方向的数轴称为x 轴或横轴，垂直方向的数轴称为y 轴或纵轴，它们称为坐标轴.两轴交点O 称为原点.在平面直角坐标系中画点P（a，b）.对于平面内任意一点P，过点P 分别向x 轴、y 轴作垂线，垂足在x 轴、y 轴上对应的数a，b分别叫做点P 的横坐标、纵坐标，有序对（a，b）叫做点P 的坐标.建立了平面直角坐标系，平面内的点就可以用一组有序实数对来表示了.在平面直角坐标系中找点A (3,-2)由坐标找点的方法：(1)先找到表示横坐标与纵坐标的点；(2)然后过这两点分别作 x 轴与 y 轴的垂线； (3)垂线的交点就是该坐标对应的点.如图，在平面直角坐标系中，两条坐标轴将坐标平面分成了四部分，右上方的部分叫做第一象限，其他三部分按逆时针方向依次叫做第二象限、第三象限、第四象限，坐标轴上的点不在任何一个象限内.观察坐标系,填写各象限内的点的坐标的特征：交流: 不看平面直角坐标系,你能迅速说出A (4,5) , B (-2,3), C (-4,-1), D (2.5,-2), E (0,-4)所在的象限吗？你的方法又是什么？ 三、 运用新知例1 写出图中的多边形ABCDEF 各顶点的坐标. 类似数轴上的点与实数是一一对应的.我们可以得出：①对于坐标平面内任意一点M ,都有唯一的一对有序实数(x ,y ) (即点M 的坐标）和它对应；②反过来，对于任意一对有序实数(x ,y ),在坐标平面内都有唯一的一点M (即坐标为(x ,y )的点）和它对应.也就是说，坐标平面内的点与有序实数对是一一对应的.例2 设点 M (a ，b ) 为平面直角坐标系内的点. (1)当 a > 0，b < 0 时，点 M 位于第几象限？A BC D EF O 11xy(2)当 ab > 0 时，点 M 位于第几象限？(3)当 a 为任意有理数，且 b < 0 时，点 M 位于第几象限？ 四、巩固新知1. 如图，点 A 的坐标为( )A . ( -2，3)B . ( 2，-3)C . ( -2，-3)D . ( 2，3)2. 如图，点 A 的坐标为 ，点 B 的坐标为 .3. 在 y 轴上的点的横坐标是______，在 x 轴上的点的纵坐标是 ______.4. 点 M （- 8，12）到 x 轴的距离是_______，到 y 轴的距离是_________ .5. 下列各点分别在坐标平面的什么位置上？A （3，6）B （0，－8）C （－7，－5）D （－6，0）E （－3.6，5）F （5，－6）G （0，0）五、归纳小结1．认识并能画出平面直角坐标系.2．在给定的直角坐标系中，由点的位置写出它的坐标. 3．能适当建立直角坐标系，写出直角坐标系中有关点的坐标.4．横（纵）坐标相同的点的直线平行于y 轴，垂直于x轴；连接纵坐标相同的点的直线平行于x轴,垂直于y轴.5．坐标轴上点的纵坐标为0；纵坐标轴上点的坐标为0.6．各个象限内的点的坐标特征是：第一象限（＋，＋）第二象限（－，＋），第三象限（－，－）第四象限（＋，－）.略.。

新苏科版八年级数学上册5.2平面直角坐标系（ 1 ）学案学习目标1、领会实际模型中确定位置的变化，会正确画出平面直角坐标系。

理解平面直角坐标系的有关概念。

2、理解平面内点的坐标的意义。

会在给定的直角坐标系中根据点的坐标标出点的位置，会根据点的位置写出点的坐标。

3、使学生了解平面上的点与有序实数对的一一对应关系。

学习重点：理解并掌握平面直角坐标系的有关概念。

在给定的直角坐标系中，根据点的坐标标出点的位置，会根据点的位置写出点的坐标。

学习难点：在给定的直角坐标系中，根据点的坐标标出点的位置，会根据点的位置写出点的坐标。

突破难点方法简述：教学过程一、情境创设（或知识回顾）1、想一想：在教室里怎样确定自己的位置？2、上电影院看电影，电影票上至少要有几个数字才能确定你的位置？3、怎样表示平面内的点的位置？二、探究学习过程导学过程平面上有＿＿＿＿且互相＿＿的2条数轴构成平面直角坐标系。

水平方向的数轴称为＿＿＿，竖起直方向的数轴称为＿＿＿，公共原点称为＿＿＿。

写出某点的坐标时，＿＿＿应写在＿＿＿＿的前面。

对于坐标平面内的任一点，都有唯一一对有序实数与它对应典型例题例1.在直角坐标系中，描出下列各点的位置。

A（3,1） B（－2,4） C（－4，－2）D（3，－2）E（0,1） F（－4,0）O（0，0）G（1,3） H（4，－2）-2-121-2-121例2.写出图中的多边形ABCDEF各个顶点的坐标。

变式训练已知点A（a,b）若点A在第一象限，则a＿0，b＿0若点A在第二象限，则a＿0，b＿0若点A在第三象限，则a＿0，b＿0若点A在第四象限，则a＿0，b＿0若点A在x轴的负半轴上，则a＿0，b＿0若点A在y轴的正半轴上，则a＿0，b＿0三、当堂检测1.若电影院座位中的8排10号用（8,10），那么10排8座可用＿＿＿表示，（5,4）指＿＿排＿＿座。

2. 点A(一l，4)在第＿象限，B(－1，一4)在第＿＿象限；点C(1，－4)在第＿＿象限，D(1，4)在第＿＿象限；点E(－2，0)在轴上，点F(0，一2)在＿＿轴上3．下列点中，位于直角坐标系第二象限的点是（）．A.（2，1）B.（-2，-1）C.（-2，1）D.（2，-1）4. 在方格纸上有A、B两点，若以B点为原点建立直角坐标系，则A点坐标为（2，5），若以A 点为原点建立直角坐标系，则B点坐标为（）A.（―2，―5）B.（―2，5）C.（2，―5）D.（2，5）5. 有甲、乙、丙三人所处位置不同。

5.2平面直角坐标系导学案《5.2 平面直角坐标系导学案》这是优秀的教学设计文章，希望可以对您的学习工作中带来帮助！作业内容5.2平面直角坐标系导学案班级：姓名：日期主备人：肖文全学习目标:1.通过实际问题生成平面直角坐标系，理解平面直角坐标系及相关概念;2.通过设计由点的位置写出点的坐标，根据坐标描出点的教学环节，理解平面直角坐标系上的点与有序数对之间的一一对应关系;3.通过对点的坐标按符号分类，观察同一类别的点的位置，理解象限及平面直角坐标系中点的位置与坐标符号的规律.导学提纲：一、阅读课本120～122页，回答下列问题：(用3分钟的时间完成导学提纲1.)确定一个物体的位置可以用1对有序实数对，为此今天我们一起来学习重要数学工具——平面直角坐标系。

1.平面直角坐标系(如图①)平面内两条__________的数轴构成平面直角坐标系.水平的数轴叫______或_______，向_______为正方向;铅直方向的数轴叫_______或_______，向_______为正方向，两轴的交点O称为_______，两条坐标轴将坐标平面分成的四个区域称为_______.请补充图①.学生活动：(1)各小组在组长带领下相互交流讨论;(2)在小组内没有解决的问题，做好记号以备提问;(3)对其他同学未解决的问题，相互帮助补充解决.2.点的坐标与点的位置(1)已知点的坐标，确定点的位置如图②，已知平面内一点P的坐标为(a，b)，如何确定P的位置呢?过在_______轴上表示a的点作_______轴的垂线，再过_______轴上表示b的点作______轴的垂线，两条垂线的交点即为点P，记为_______.(2)已知点的位置，确定点的坐标如图②，已知平面直角坐标系内一点Q，该如何确定点Q的的坐标?过点Q分别作x轴、y轴的_______，与x轴的交点表示的实数记为点Q的_______坐标，与y轴的交点表示的实数记为点Q的_______坐标.将这一对有序实数(m，n)记为点Q的坐标，即Q(m，n).请在图②中补充点Q的坐标.3.点的坐标的特点(1)象限内的点(2)坐标轴上的点①x轴上点的纵坐标是_______，一般记为(x,0);②y轴上点的横坐标是_______，一般记为(0,y);③原点处点的坐标为(_____，_____).拓展：(3)角平分线上的点二、典例精析例1.在直角坐标系中，描出下列各点的位置。

自学互学导学评学《5.2平面直角坐标系（1）》导学案汶源学校初二数学备课组【学习目标：】1. 认识平面直角坐标系，了解相关概念，能画出平面直角坐标系。

2 •能在给定的直角坐标系中，由点的位置写出它的坐标，由坐标找出点的位置，体会数形结合思想，发展审美观。

3•探索各象限内及坐标轴上点的坐标特点，能应用其解决简单问题。

【学习过程】一、情景导入，认定目标：同学们，下面是我们学校的平面示意图，你们能用上一节课学习的确定位置方法给大家介绍一下我们学校各个场所的位置吗？二、自学引领发现问题阅读课本（119页中间部分和120页下边部分）完成以下导学案上的自学任务：1 •什么是直角坐标系？2 •尝试画出一个直角坐标系，并标出横轴（x轴）、纵轴（y轴）、坐标原点。

3 •平面直角坐标系将平面分成了几部分？说出各部分的名称，并在你所画的坐标系中表示出来。

三、合作探究教师点拨探究一：由点找坐标1）坐标系内有任意一点A,过点A向x轴做垂线，在0 1 23456789 10 11 12横轴上对应的数叫做点A的____________ , （2）过点A向y轴做垂线，在y轴上对应的数叫做点A的_ 在写时，横坐标在，纵坐标在，用用起来。

跟踪练习一：写出图中_o 3）隔开，A: A、B、C D E各点的坐-4 -3 -2 -1-1C: D ：E: F ：G:探究二：由坐标找点跟踪练习二：在直角坐标系中描出下列各组点，并将各组点用线段依次连接起来自学互学导学评学(0,2 ) (3,4 ) (5,3 ) (6,0 ) (4, -3) (2, -4) (0, -5) (-2,-4 ) (-4,-3)(-6,0)(-5,3)(-3,4)(0,2)点的位置横坐标符号纵坐标符号第一象限第二象限第三象限第四象限探究三：平面直角坐标系内点的坐标特点观察上图中各点的坐标,回答下列问题:(1) 哪些点位于第一象限象限？它们的横、纵坐标的符号有什么特点？第二象限、第三象限、第四象限呢？小组合作，完成表格。

《平面直角坐标系》教案精选平面直角坐标系教案。

教案课件在老师少不了一项工作事项，这就要老师好好去自己教案课件了。

教案是落实教学目标的有效手段，写一篇教案课件要具备哪些步骤？下面是我为大家整理的关于“《平面直角坐标系》教案”的资料，请保藏好，以便下次再读！《平面直角坐标系》教案篇1教学目标：1、理解平面直角坐标系的意义；把握在平面直角坐标系中刻画点的位置的方法。

2、把握坐标法解决几何问题的步骤；体会坐标系的作用。

教学难点：能够建立适当的直角坐标系，解决数学问题。

情境1：为了确保宇宙飞船在预定的轨道上运行，并在按方案完成科学考察任务后，平安、精确的返回地球，从火箭升空的时刻开头，需要随时测定飞船在空中的位置机器运动的轨迹。

情境2：运动会的开幕式上经常有大型团体操的表演，其中不断变化的背景图案是由看台上座位排列整齐的人群不断翻动手中的一本画布构成的。

要消失正确的背景图案，需要缺点不同的画布所在的位置。

在平面上，当取定两条相互垂直的直线的交点为原点，并确定了度量单位和这两条直线的方向，就建立了平面直角坐标系。

它使平面上任一点P 都可以由惟一的实数对（x，y）确定。

在空间中，选择两两垂直且交于一点的三条直线，当取定这三条直线的交点为原点，并确定了度量单位和这三条直线方向，就建立了空间直角坐标系。

它使空间上任一点P都可以由惟一的实数对（x，y，z）确定。

三、讲解新课：1、建立坐标系是为了确定点的位置，因此，在所建的坐标系中应满意：任意一点都有确定的坐标与其对应；反之，依据一个点的坐标就能确定这个点的位置例1选择适当的平面直角坐标系，表示边长为1的正六边形的顶点。

如何通过它们到点O的距离以及它们相对于点O的方位来刻画，即用”距离和方向”确定点的位置例2已知B村位于A村的正西方1公里处，原方案经过B村沿着北偏东60的方向设一条地下管线m、但在A村的西北方向400米出，发觉一古代文物遗址W、依据初步勘探的结果，文物管理部门将遗址W四周100米范围划为禁区、试问：埋设地下管线m的方案需要修改吗？1一炮弹在某处爆炸，在A处听到爆炸的时间比在B处晚2s，已知A、B 两地相距800米，并且此时的声速为340m/s，求曲线的方程2在面积为1的中，，建立适当的坐标系，求以M，N为焦点并过点P的椭圆方程通过平面变换可以把曲线变为中心在原点的单位圆，恳求出该复合变换？2、利用平面直角坐标系解决相应的数学问题。

《平面直角坐标系》教学案学习目标：1、认识到建立平面直角坐标系的必要性，并能画出平面直角坐标系；2、能在方格纸上建立适当的直角坐标系，描述物体的位置；3、在给定的直角坐标系中，会根据坐标描出点的位置、由点的位置写出它的坐标．4、经历画坐标系、描点、连线、看图以及由点找坐标等过程，发展数形结合意识、合作交流意识。

问题引入1.平面直角坐标系定义：在平面内，两条____________且有公共_________的数轴组成平面直角坐标系，简称_________________。

通常，两条数轴分别置于水平位置与铅直位置，取__________和__________的方向分别为两条数轴的正方向，水平的数轴叫做_______或_______，铅直的数轴叫做_______或_______，两者统称为_______，它们的公共原点O 称为直角坐标系的_______。

2.如图，对于平面内任意一点P ，过点P 分别向x 轴，y 轴作_______，垂足在x 轴、y 轴上对应的数a ，b 分别叫做点P 的_______、_______，有序数对（a ，b ）叫做点P 的_______。

活动1：探究坐标系1（1）如图1是某市的旅游示意图，在科技大学处的你如何向来访的朋友介绍该市几个风景点的位置呢?尽可能给出简洁的表示方法，并与同伴交流。

大成殿： ， 中心广场： ， 碑林 ： 。

(排版说明:加上比例尺，一格表示100m)（2）小明用（0,0）表示科技大学的位置，用（2，5）表示大成殿，你理解他的意思吗？试表示出图中其他点的位置。

（3）按照小明的方法，（5,2）表示 ，（5,2）中的2表示 ，（2,5）中的2表示 。

（4）如果城市比较大，地图还需要向右上部分扩展，你能类似地表示右上部分其他点的位置吗？2（1）站在中心广场的小亮，以中心广场为“原点”，怎样用数对表示各景点的位置呢？碑林 ： ， 大成殿：，科技大学： 。

（2）如果这个图向四面八方扩展，可以得到一个覆盖整个平面的“地图”。

《平面直角坐标系》的教案（精选5篇）《平面直角坐标系》的教案（精选5篇）作为一名优秀的教育工作者，时常要开展教案准备工作，教案有助于顺利而有效地开展教学活动。

那么你有了解过教案吗？下面是小编收集整理的《平面直角坐标系》的教案（精选5篇），欢迎大家借鉴与参考，希望对大家有所帮助。

《平面直角坐标系》的教案1[教学目标]1、认识平面直角坐标系，了解点的坐标的意义，会用坐标表示点，能画出点的坐标位2、渗透对应关系，提高学生的数感。

[教学重点与难点]重点：平面直角坐标系和点的坐标。

难点：正确画坐标和找对应点。

[教学设计][设计说明]一、利用已有知识，引入1．如图，怎样说明数轴上点A和点B的位置，2．根据下图，你能正确说出各个象棋子的位置吗？二、明确概念平面直角坐标系：平面内画两条互相垂直、原点重合的数轴，组成平面直角坐标系（rectangular coordinate system）。

水平的数轴称为x轴（x—axis）或横轴，习惯上取向右为正方向；竖直的数轴为y轴（y—axis）或纵轴，取向上方向为由数轴的表示引入，到两个数轴和有序数对。

从学生熟悉的物品入手，引申到平面直角坐标系。

描述平面直角坐标系特征和画法正方向；两个坐标轴的交点为平面直角坐标系的原点。

点的坐标：我们用一对有序数对表示平面上的点，这对数叫坐标。

表示方法为（a，b）。

a是点对应横轴上的数值，b是点在纵轴上对应的数值。

例1 写出图中A、B、C、D点的坐标。

建立平面直角坐标系后，平面被坐标轴分成四部分，分别叫第一象限，第二象限，第三象限和第四象限。

你能说出例1中各点在第几象限吗？例2 在平面直角坐标系中描出下列各点。

（）A（3，4）；B（—1，2）；C（—3，—2）；D（2，—2）问题1：各象限点的坐标有什么特征？练习：教材49页：练习1，2、三。

深入探索教材48页：探索：识别坐标和点的位置关系，以及由坐标判断两点的关系以及两点所确定的直线的位置关系。