关于镜像法与电轴法静电场课件

Topic # 8—镜像法(method ofimages)­Part1n镜像法n点电荷~无限大的接地导板系统n电轴~无限大接地导电平面系统的电场n电轴法 (广义镜像法)1n镜像法n定义The method of images is an analytical technique that involves replacing constant­potential surfaces with equivalent sources called image sources that generate the same fields.镜像法——用场域闭合边界外虚设的较简单的电荷分布来等效替代该边界上未知的较为复杂的电荷分布以简化原问题的分析和计算。

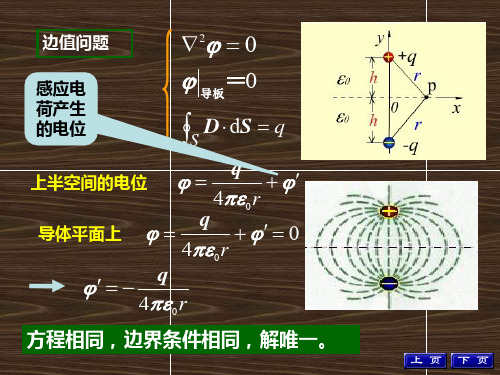
场域闭合边界—一般为导体组成等位面2n镜像法n适用场合The conducting boundaries that can be modeled inthis way include infinite planes, spheres, infinitecylinders, and wedges.34n 点电荷~无限大的接地导板系统 n Background对于大地上方输电线、雷电形成的电场，可以典型化为最 基本的问题：无限大接地导体上方点电荷激发的电场问题+q2s DP (x,y,z )1s he 导板¥r 2 0j Ñ=5n 点电荷~无限大的接地导板系统 n 分析—直接求解是否可能1. ? 不行，2. 已知场源分布，求3. 高斯定理？0 4 P qrj e = p E vd SE S · ò vv Ñ0 E S × 或 非单一媒质需要探索新的求解方法不通6n 点电荷~无限大的接地导板系统n 换一个角度考虑：考虑其边值问题20 in Dj Ñ= 1||0S j j == 导板表面 |0t E = 导板表面 211221 10 00 d d s C s s S S q n j j s e = ®® ¶ ====-= ¶ òò ÑÑ7n 点电荷~无限大的接地导板系统 n 能否找到较简单的等效模型？一对相距2h 位于e 0 单一媒质的上半空间的电场—仅考虑上半空间 q+ 2s 1s h0 e ¥e hq- 2 2 0j Ñ= xy o Er边值问题22 0 ()j Ñ= 在上半空间 12 |0S j = 0 | y n n E E e= = r r8n 点电荷~无限大的接地导板系统 n 能否找到较简单的等效模型？一对相距2h 位于e 0 单一媒质的上半空间的电场—仅考虑上半空间 边值问题22 0 ()j Ñ= 在上半空间 1 2 |0 S j = 0 | y n nE E e = = r r y =0的平面为等位面，且其电位为零9n 点电荷~无限大的接地导板系统 n 能否找到较简单的等效模型？一对相距2h 位于e 0 单一媒质的上半空间的电场—仅考虑上半空间 22122210 00 d d s C s s S S q n j j s e = ®® ¶ ====-= ¶ òò ÑÑ 在正点电荷处取同样“大小”的面元S 2，可近似认为该 面元为等位面，于是：q+ 2s 1s h0 e ¥e hq- 2 2 0j Ñ= xy o Er10n 点电荷~无限大的接地导板系统 n 比较边值问题一对相距2h 位于e 0 单一媒质的上半空间的电场原问题22 0 () j Ñ= 在上半空间 1 220 ||=0S y j j = =0 |0t y E = = 22122 210 00 d d s C s s S S q n j j s e = ®®¶ ====-= ¶ òò ÑÑ 20 in Dj Ñ= 1||0S j j == 导板表面 |0t E = 导板表面 21122110 00 d d s C s s S S q n j j s e = ®® ¶ ====-= ¶ òò ÑÑ 二者完全一样（y =0平面对应导板表面）11n 点电荷~无限大的接地导板系统 n 结论由唯一性定理可知，两者的解答 j =j 2注意适用区域：仅上半平面？为什么？计算导板上方的电场时，可以把导板上的感应电荷的影响 用一置于对称位置上的集中电荷等效由于引入的电荷位于原电荷对导板的镜像处—镜像法n点电荷~无限大的接地导板系统 n计算模型—原问题De导体j = x1ryo(,,0)P x yq+h1213n 点电荷~无限大的接地导板系统 n 计算模型—镜像法模型场中电场分布,等效于引入镜 像电荷q ，撤去 导板，整个空 间充满同一种 电介质的电场。

Topic # 9—镜像法(method ofimages)­Part2n电轴法 (广义镜像法)n点电荷~ 无限大介质平面系统的电场n点电荷 ~ 导体球 (球面镜像法）1n计算n等位线在xoy平面内，等位线轨迹是一族偏心圆就每个等位圆轨迹而言，半径a，圆心至原点的距离h，线 电荷至原点的距离b，三者间的关系式为：h 2 = a 2 + b 2∴ a 2 = h 2 - b 2 =( h + b )( h - b)即 (±t) 电轴位置对每个等位圆的圆心来说，互为反演点。

23n 计算n 等位线­图示1K oyxt+ t- b1 h 2h 3h b2 K 3K 31 K2 1 K 1 1 K1 a 2a 3an计算n启示n如果一静电场的等位线为一族偏心圆，其电场的计算问题，可考虑等效为一对正负电轴产生的电场n电轴的位置则由上面的a,b,h关系式确定n由于共有a,b,h三个参数，因此至少给出2个等位圆，才能确定电轴的位置。

n按已知2个等位圆的不同，可得不同的等效计算模型。

45n 同半径的两线输电线电场 n 问题半径为a 的两输电线分别带有等量异号的线电荷 （±t ），计算其产生的电场oyt+ t- aa1o 2o dxn同半径的两线输电线电场n分析输电线是导体，导体为等位体、导体表面为等位面 在xoy平面，两导体的圆表面迹线为等位线等位线为同半径的两个偏心圆可用一对电轴模型计算原场的分布67n 同半径的两线输电线电场 n 电轴法模型参数b,h 必须满足相距为d 半径分别为a 的两个圆为等位 圆，即已知等位圆半径a , 等位圆圆心之间的距离d ，确 定线电荷（电轴）至原点的距离b 和y 轴的位置变量h2d h =o a a 1o 2o dxhhbb22222 d b h a aæö =-=- ç÷ èø8n 同半径的两线输电线电场 n 镜像法模型oy t+ t- b hbdxh 1r 2r (,)P x y a电轴 ±t 的位置 22222 d b h a aæö =-=- ç÷ èø9n 同半径的两线输电线电场 n 镜像法模型oyt+ t- b hbdxh 1r 2r (,)P x y a适用区域那个区域没有引入电荷==适用于那个区域不包含同半径两 导体的所有区域 任意点电位2 01ln2 P r tj e r = p10n 两个不同半径的两线输电线电场 n 问题t+ t- d1a 2o 1o 2a11n 两个不同半径的两线输电线电场 n 已知条件n 待求量oy t+ t- bb dx1r 2r (,)P x y 1 a b 1h 2h b2o 1o 2a 两等位圆半径 a 1 、a 2，及其圆心间的距离 d 两圆心与原点的距离h 1 、h 2、线电荷与原点的距离 b12n 两个不同半径的两线输电线电场 n 已知与待求量的关系h 2 = a 2 + b2 22211 b h a=- 12d h h =+ 222 22b h a =- oy t+ t- b b dx1r 2r (,)P x y 1 a b 1h 2h b2o 1o 2a13n 两个不同半径的两线输电线电场 n 已知与待求量的关系222 121 222 212 2 2 d a a h d d a a h d +- =+- =2222 1122b h a h a=-=- oyt+ t- b b dx1r 2r (,)P x y 1 a b 1h 2h b2o 1o 2a 适用区域 不包含不同半径两导体内区域14n 偏心电缆的电场 n 问题d1 a 1o 2o 2a t+ t-15n 偏心电缆的电场 n 分析仍可应用电轴法。