差异显著性检验t检验

参数显著性检验公式t检验F检验的计算公式参数显著性检验公式——t检验、F检验的计算公式在统计学中，参数显著性检验是一种用于验证模型参数是否显著的方法。

在进行参数显著性检验时，我们可以使用t检验或F检验来计算参数的显著性。

一、t检验公式t检验用于检验一个样本的均值是否与总体均值存在显著差异，或者用于检验两个样本的均值是否存在显著差异。

其计算公式如下：t = (x - μ) / (s / √n)其中，t为t值，x为样本均值，μ为总体均值，s为样本标准差，n为样本容量。

根据t检验的结果，我们可以通过查表或计算获得对应的p值，进而判断参数的显著性。

二、F检验公式F检验主要用于检验两个或多个样本方差是否存在显著差异。

其计算公式如下：F = (s1² / s2²)其中，F为F值，s1²为第一个样本的方差，s2²为第二个样本的方差。

同样地，根据F检验的结果，我们可以通过查表或计算获得对应的p 值，从而判断参数的显著性。

需要注意的是，t检验和F检验都是基于假设检验的方法。

在进行参数显著性检验时，我们需要先设定原假设和备择假设，并通过计算得到的t值或F值与对应的临界值进行比较，最终得出对参数的显著性结论。

总结起来，参数显著性检验公式中的t检验和F检验是常用的统计方法，用于判断参数的显著性。

通过计算得到的t值或F值与对应的临界值进行比较，可以得出对参数显著性的结论。

在实际应用中，我们可以根据数据类型和问题特点选择合适的显著性检验方法，并利用相应的计算公式进行计算。

这些检验方法在科学研究、社会调查和数据分析等领域具有广泛的应用。

显著性差异分析显著性差异分析是统计学中常用的一种方法，用于确定两个或多个样本之间是否存在显著性差异。

这种分析方法可以帮助研究人员确定研究对象在不同条件下的表现是否存在实质性的差异，从而为科学研究和决策提供依据。

本文将介绍显著性差异分析的基本原理、相关统计指标以及实际应用案例。

一、基本原理显著性差异分析基于假设检验的思想，通过对比不同观测值之间的差异，判断是否存在实质性的差异。

在进行显著性差异分析时，通常会制定一个原假设（H0）和一个备选假设（H1）。

原假设认为观测值之间不存在显著性差异，备选假设则认为观测值之间存在显著性差异。

二、相关统计指标在显著性差异分析中，常用的统计指标包括均值、方差和标准差。

均值用于衡量不同样本之间的平均表现，方差和标准差则用于衡量不同样本之间的离散程度。

此外，还有一些统计指标如t值、p值和置信区间等，用于判断差异是否达到统计学上的显著性。

三、实际应用案例显著性差异分析在各个领域都有广泛的应用。

以下以医学领域为例，介绍显著性差异分析的一个实际案例。

研究人员想要比较两种不同药物对患者血压的影响是否存在显著性差异。

他们随机选取了100名患者，并将其分成两组，一组服用药物A，另一组服用药物B。

他们在实验开始前和结束后分别对患者的血压进行测量，得到了如下结果：药物A组：初始平均血压为120 mmHg，终止平均血压为110 mmHg。

药物B组：初始平均血压为122 mmHg，终止平均血压为115 mmHg。

为了确定这两组数据之间的差异是否显著，研究人员进行了显著性差异分析。

他们首先计算了每组的均值和标准差，然后使用t检验进行了统计显著性检验。

经过计算和统计分析，研究人员得到了以下结果：药物A组和药物B组之间的平均差异为2 mmHg，标准差为3 mmHg。

根据t检验的结果，他们得到了t值为1.33，p值为0.187。

根据统计结果可知，p值大于显著性水平（通常为0.05），即在此次研究中未能找到药物A和药物B之间的显著性差异。

几种常见的显著性检验方法常见的显著性检验方法有单样本t检验、双样本配对t检验、双样本独立t检验、方差分析（ANOVA）、卡方检验和皮尔逊相关分析。

本文将对每种显著性检验方法进行详细介绍。

单样本t检验是一种用于检验一个样本均值是否显著不同于一些给定的总体均值的统计方法。

该方法的原理是将样本均值与总体均值进行比较，计算出一个t值。

根据t值的大小和自由度，可以查找相应的临界值，从而得出显著性检验的结果。

双样本配对t检验也称为相关样本t检验，用于比较两个相关样本或两个相关变量之间的均值差异是否显著。

该方法的原理是将两个相关样本的均值差异与零进行比较，计算出一个t值。

根据t值的大小和自由度，可以查找相应的临界值，从而得出显著性检验的结果。

双样本独立t检验用于比较两个独立样本或两个独立变量之间的均值差异是否显著。

该方法的原理是将两个独立样本的均值差异与零进行比较，计算出一个t值。

根据t值的大小和自由度，可以查找相应的临界值，从而得出显著性检验的结果。

方差分析（ANOVA）是一种用于比较两个或更多个样本或组之间均值差异是否显著的统计方法。

该方法的原理是将不同组之间的均值差异与总均值差异进行比较，计算出一个F值。

根据F值的大小和自由度，可以查找相应的临界值，从而得出显著性检验的结果。

卡方检验用于比较观察频数与期望频数之间的差异是否显著。

该方法的原理是通过计算观察频数和期望频数之间的卡方值，进而判断观察频数是否与期望频数存在显著差异。

皮尔逊相关分析用于评估两个变量之间的线性关系是否显著。

该方法的原理是通过计算两个变量之间的皮尔逊相关系数，从而判断变量之间的关系是否显著。

需要注意的是，在进行显著性检验时，首先需要确定假设，即原假设和备择假设。

原假设通常表示为没有显著差异或没有关系，备择假设则表示存在显著差异或存在关系。

根据样本数据计算出的检验统计量与临界值进行比较，如果检验统计量落在拒绝域（即临界值的范围内），则拒绝原假设，认为差异或关系是显著的。

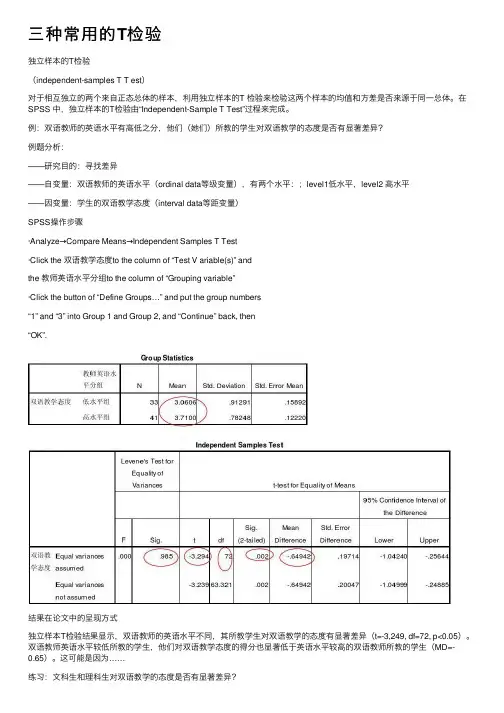
三种常⽤的T检验独⽴样本的T检验（independent-samples T T est）对于相互独⽴的两个来⾃正态总体的样本，利⽤独⽴样本的T 检验来检验这两个样本的均值和⽅差是否来源于同⼀总体。

在SPSS 中，独⽴样本的T检验由“Independent-Sample T Test”过程来完成。

例：双语教师的英语⽔平有⾼低之分，他们（她们）所教的学⽣对双语教学的态度是否有显著差异？例题分析：——研究⽬的：寻找差异——⾃变量：双语教师的英语⽔平（ordinal data等级变量），有两个⽔平：；level1低⽔平，level2 ⾼⽔平——因变量：学⽣的双语教学态度（interval data等距变量）SPSS操作步骤·Analyze→Compare Means→Independent Samples T Test·Click the 双语教学态度to the column of “Test V ariable(s)” andthe 教师英语⽔平分组to the column of “Grouping variable”·Click the button of “Define Groups…” and put the group numbers“1” and “3” into Group 1 and Group 2, and “Continue” back, then“OK”.结果在论⽂中的呈现⽅式独⽴样本T检验结果显⽰，双语教师的英语⽔平不同，其所教学⽣对双语教学的态度有显著差异（t=-3,249, df=72, p<0.05）。

双语教师英语⽔平较低所教的学⽣，他们对双语教学态度的得分也显著低于英语⽔平较⾼的双语教师所教的学⽣（MD=-0.65）。

这可能是因为……练习：⽂科⽣和理科⽣对双语教学的态度是否有显著差异？配对样本T检验（Paired-samples T Test）配对样本T检验，⽤于检验两个相关的样本（配对资料）是否来⾃具有相同均值的总体。

显著性差异计算公式
1显著性差异计算
显著性差异计算是一种统计学上的重要概念，它的主要目的是用数字计算出不同样本之间的差异大小、程度和其是否有统计学意义。

显著性差异计算的统计学意义在于，当两个样本之间的差异足够显著时，我们可以说这两个样本之间有显著的差异，从而对该问题做出更正确的研究和决策。

2显著性差异计算公式
显著性差异计算公式用来计算两个样本之间的显著性差异，这里主要分为t检验和z检验，其公式分别为：
t检验公式：t=(x1–x2)/(s21/n1+s22/n2)
z检验公式：z=(x1–x2)/s
其中：x1和x2分别是两个样本均值，n1和n2是两个样本的样本量，s21和s22是样本1和样本2的样本方差，s为两个样本均值方差的平方根。

3显著性差异计算的应用
显著性差异计算的应用非常广泛，并发挥着重要作用。

一般采用t 检验的情况比较多，用来比较两个独立性样本的均值是否有显著差异。

另外，z检验通常在测量总体平均值时使用，其目的在于测定样品
的数量是否足够大。

而且在一些混合分析中，显著性差异计算也可以用来准确判断两个不同组年组间的差异程度。

显著性差异计算在医学研究中也有着重要作用，比如药物研发和临床试验中都可能使用显著性差异计算来判断药物对病患的有效度。

此外，显著性差异计算还可用于媒体报道、教学研究等多种领域。

可见显著性差异计算是一项重要的统计学知识，它可以用来计算两个样本之间的显著性差异，是科学研究和现实决策中不可或缺的一项工具。

几种常见的显著性检验方法显著性检验是统计学中常用的一种方法，用于检验两组或多组数据之间是否存在显著差异。

下面将介绍几种常见的显著性检验方法。

1.t检验：t检验用于比较两组均值是否存在显著差异。

根据独立样本或配对样本可以分为独立样本t检验和配对样本t检验。

适用于连续型变量，要求样本满足正态分布和方差齐性的假设。

2.方差分析（ANOVA）：方差分析用于比较三组或多组均值是否存在显著差异。

适用于连续型变量，要求样本满足正态分布和方差齐性的假设。

方差分析包括单因素、多因素、重复测量、混合设计等多种类型。

3.卡方检验：卡方检验用于比较两个或多个分类变量之间是否存在显著差异。

适用于分类变量，比如性别、职业等。

卡方检验可用于检验两个分类变量之间的关联性，也可用于检验一个分类变量与一个连续型变量之间的关系。

4.相关分析：相关分析用于评估两个连续型变量之间的关系强度和方向。

常用的相关系数有皮尔逊积矩相关系数、斯皮尔曼秩相关系数和判定系数等。

相关系数的显著性检验可以帮助确定两个变量之间是否存在显著相关关系。

5.回归分析：回归分析用于建立一个或多个自变量和一个连续型因变量之间的函数关系，并用于预测因变量。

回归分析中常用的显著性检验方法有t检验、F检验和R平方检验等。

6. 生存分析：生存分析主要用于评估时间至事件发生（比如死亡、疾病复发等）之间的关系。

生存分析的主要方法有Kaplan-Meier生存曲线和Cox比例风险模型等。

生存分析通常使用对数秩检验来评估不同组别之间的显著差异。

除了以上常见的显著性检验方法，还有一些其他的检验方法，比如非参数检验（如Mann-Whitney U检验、Wilcoxon符号秩检验）、Fisher精确检验、Bootstrap检验等，这些方法适用于不满足正态分布假设或方差齐性假设的数据情况。

显著性检验方法的选择要根据数据的类型和应用背景来决定。

在进行显著性检验时，还需注意样本的大小、假设检验的前提条件以及是否需要对多重比较进行校正等问题。

生物统计学实验报告T检验T检验是一种用于比较两个样本均值是否有显著差异的统计方法。

在生物统计学中，T检验经常被用于比较实验组和对照组在某个特定变量上的差异，以确定是否存在显著差异。

T检验的基本原理是通过计算两个样本的均值和方差，然后应用统计学中的t分布来判断两个样本均值是否有显著差异。

在进行T检验之前，需要明确以下几个方面的内容：假设检验的零假设和备择假设、显著性水平、检验的类型（单尾检验或双尾检验）以及样本数据的收集和处理。

在进行T检验时，首先要设定零假设与备择假设。

零假设表示两个样本均值无显著差异，备择假设则表示两个样本均值存在显著差异。

接下来要设定显著性水平，通常使用的显著性水平为0.05，即p值小于0.05时，认为存在显著差异。

然后要确定T检验的类型，通常分为单尾检验和双尾检验。

单尾检验适用于预测两个样本均值的相对大小，而双尾检验适用于预测两个样本均值是否存在显著差异。

在进行T检验之前，还需要选择合适的T检验方法，主要有独立样本T检验和配对样本T检验，根据实验设计的不同选择相应的方法。

当以上设定完成后，需要收集实验数据，并计算两个样本的均值和方差。

接下来根据公式计算出T值，并据此计算出p值。

最后，根据p值与设定的显著性水平进行比较，判断两个样本均值是否存在显著差异。

如果p值小于显著性水平，则拒绝零假设，认为两个样本均值存在显著差异；如果p值大于显著性水平，则接受零假设，认为两个样本均值无显著差异。

总之，T检验是一种常用的比较两个样本均值是否有显著差异的统计方法。

在生物统计学中，T检验可以帮助我们分析实验组和对照组在某个特定变量上是否存在显著差异，从而验证实验的有效性。

然而，在进行T检验之前，需要明确假设检验的设定、显著性水平和检验类型，并正确收集和处理实验数据，以获得准确的结果。

显著性差异分析在统计学中，显著性差异分析是一种重要的方法，用于确定两个或多个组之间的差异是否具有统计学上的显著性。

这种分析方法可以帮助我们了解变量之间的关系，并对研究结果进行有效的解释和预测。

本文将介绍显著性差异分析的基本概念、应用领域以及常用的统计检验方法。

一、显著性差异分析的基本概念显著性差异分析是指在给定的置信水平下，对样本数据进行统计推断，判断两个或多个组之间的差异是否具有统计学上的显著性。

显著性差异可以帮助我们确定一个变量是否对不同组之间的差异产生影响，从而得出结论并提供指导性建议。

二、显著性差异分析的应用领域显著性差异分析广泛应用于各个领域的研究中，例如医学、教育、经济等。

以下是几个常见的应用领域：1. 医学研究：显著性差异分析可以帮助医学研究人员比较不同药物、治疗方法或者手术对疾病患者的影响，并确定哪种方法或者药物更有效。

2. 教育研究：显著性差异分析可以用于教育研究中，比较不同教学方法、教材或者学习条件对学生学业成绩的影响，以便提出教育改革和改进教学方法的建议。

3. 经济研究：显著性差异分析可以用于经济研究中，比较不同政策对经济发展的影响，从而为政策制定者提供科学依据。

三、常用的统计检验方法显著性差异分析涉及到很多统计方法和推断技术，下面介绍几种常用的统计检验方法：1. t检验：t检验是一种常用的显著性差异分析方法，适用于两个组之间的差异比较。

通过计算两组样本的均值差异以及置信区间，来判断差异是否显著。

2. 方差分析（ANOVA）：方差分析是一种适用于比较三个及以上组别之间的差异的方法，它可以帮助我们确定变量是否对组别间的差异产生显著性影响，并进行多个组别的比较。

3. 卡方检验：卡方检验适用于比较分类变量在两个或多个组别中的分布差异。

它能够帮助我们确定变量是否与组别之间的关系显著，从而进行相应的分析和解释。

四、结论显著性差异分析是统计学中一项重要的工具，它可以帮助我们确定多组数据之间的差异是否显著，并为决策者提供科学的依据。

几种常见的显著性检验方法显著性检验是统计学中常用的一种方法，用于判断样本数据是否由一个总体生成，或者判断两个或多个样本数据是否来自同一个总体。

它的主要目的是通过计算样本数据之间的差异，并基于概率理论判断这些差异是否由随机因素引起，从而得出结论。

下面将介绍几种常见的显著性检验方法：1.t检验：t检验是一种常用的参数检验方法，用于判断两个样本均值是否有显著差异。

当总体的方差未知时，可以使用独立样本t检验；当总体的方差已知时，可以使用配对样本t检验。

2.方差分析：方差分析是一种用于比较两个或多个样本均值是否有显著差异的方法。

它通过比较组间变异与组内变异来判断均值的差异是否有统计学意义。

常用的方差分析方法包括单因素方差分析和多因素方差分析。

3.卡方检验：卡方检验是一种用于比较观察值与期望值之间的差异是否有显著性的非参数检验方法。

它适用于分类数据的分析，常用于分析两个或多个分类变量之间的关联性。

4.相关分析：相关分析是一种用于衡量两个变量之间相关关系的方法，常用于测量变量之间的线性相关性。

通过计算相关系数来判断两个变量是否存在显著的相关关系。

5.回归分析：回归分析是一种用于研究自变量与因变量之间关系的方法。

通过拟合回归模型并进行参数估计，可以判断自变量对因变量的影响是否显著。

除了上述几种常见的显著性检验方法外，还有其他一些方法，如非参数检验方法（如Wilcoxon秩和检验和Mann-Whitney U检验）、生存分析中的log-rank检验等。

在实际应用中，应根据具体问题选择适当的检验方法，并进行合理的假设设置和数据分析，以得出准确的结论。

t检验(t-test)临界值表-t检验表t检验(t-test)临界值表-t检验表t检验是一种统计方法，用于比较两个样本均值之间是否存在显著差异。

在进行t检验时，需要计算样本均值、样本标准差、样本大小等数据，并根据t值和自由度查找t检验表中的临界值，以确定是否拒绝零假设。

以下是t检验(t-test)临界值表-t检验表，用于确定临界值和p值：自由度| 0.10| 0.05| 0.025| 0.01| 0.005|------| -----| -----| -----| ----| ----|1| 3.08| 6.31| 12.71| 31.82| 63.66|2| 1.89| 2.92| 4.30| 6.96| 9.93|3| 1.64| 2.35| 3.18| 4.54| 5.84|4| 1.53| 2.13| 2.78| 3.75| 4.60|5| 1.48| 2.02| 2.57| 3.36| 4.03|6| 1.44| 1.94| 2.45| 3.14| 3.71|7| 1.41| 1.89| 2.37| 2.98| 3.50|8| 1.40| 1.86| 2.31| 2.90| 3.36|9| 1.38| 1.83| 2.26| 2.82| 3.25|10| 1.37| 1.81| 2.23| 2.76| 3.17|11| 1.36| 1.80| 2.20| 2.71| 3.11|12| 1.36| 1.78| 2.18| 2.68| 3.06|13| 1.35| 1.77| 2.16| 2.65| 3.01|14| 1.35| 1.76| 2.14| 2.62| 2.98|15| 1.34| 1.75| 2.13| 2.60| 2.95|16| 1.34| 1.75| 2.12| 2.58| 2.92|17| 1.33| 1.74| 2.11| 2.57| 2.90|18| 1.33| 1.73| 2.10| 2.55| 2.88|19| 1.33| 1.73| 2.09| 2.54| 2.86|20| 1.33| 1.72| 2.09| 2.53| 2.85|21| 1.32| 1.72| 2.08| 2.52| 2.83|22| 1.32| 1.71| 2.07| 2.51| 2.82|23| 1.32| 1.71| 2.07| 2.50| 2.81|24| 1.32| 1.70| 2.06| 2.49| 2.80|25| 1.32| 1.70| 2.06| 2.48| 2.78|26| 1.31| 1.70| 2.06| 2.48| 2.77|27| 1.31| 1.69| 2.05| 2.47| 2.76|28| 1.31| 1.69| 2.05| 2.46| 2.76|29| 1.31| 1.69| 2.05| 2.46| 2.75|30| 1.31| 1.68| 2.04| 2.45| 2.74|在使用t检验表进行统计分析时，需要先确定自由度，然后查找表中对应的临界值。

使用SPSS 进行两组独立样本的t检验、F检验、显著性差异、计算p值SPSS版本为SPSS 20.如有以下两组独立的数据，名称分别为“111”，“222”。

111组：4、5、6、6、4222组：1、2、3、7、7首先打开SPSS，输入数据，命名分组，体重和组名要对应，111组的就不要输入到222组了。

数据视图如下：变量视图如下，名称可以改成“分组嗷嗷嗷”“体重喵喵喵”等点击“分析”-“比较均值”-“独立样本T检验”来到这里，分组变量为“分组嗷嗷嗷”，检验变量为“体重喵喵喵”。

【关键的一步】点击分组嗷嗷嗷，进行“定义组”【关键的一步】输入对应的两组数据的组名：“ 111”和“222”点击确定，可见数据与组名对应上了。

点击“确定”，生成T检验的报告，即将大功告成！第一个表都知道什么回事就不缩了，excel都能实现的。

第二个表才是重点，不然用SPSS干嘛。

F检验：在两样本t检验中要用到F检验，F检验又叫方差齐性检验，用于判断两总体方差是否相等，即方差齐性。

如图：F旁边的 Sig的值为.007 即0.007， <0.01, 即两组数据的方差显著性差异！看到“假设方差相等”和“假设方差不相等”了么？此时由于F检验得出Sig <0.01，即认为假设方差不相等！因此只关注红框中的数据即可。

如图，红框内，Sig（双侧），为.490即0.490，也就是你们要求的P值啦，Sig ( 也就是P值 ) >0.05，所以两组数据无显著性差异。

PS：同理，如果F检验的Sig >.05（即>0.05），则认为两个样本的假设方差相等。

所以相应的t检验的结果就看上面那行。

by 20150120 深大医学院 FG。

显著性差异计算公式什么是显著性差异？简而言之，显著性差异，即“显著性差异”，指的是两个或多个指标之间的差异及其显著性，是衡量两个或多个指标之间具有显著性差异的指标。

ゲム同样，当一个研究者推断两组样本之间的显著性差异时，应考虑它们之间的差异是否真的存在。

显著性差异的计算方法有很多，但是最常用的计算方法是t检验，z检验和卡方检验。

其中，t检验是最常用的方法，可以用来测量两个分组之间的显著性差异，而z检验和卡方检验可以用来测量多个分组之间的显著性差异。

t检验是一种两比较检验，也就是说，它可以用来比较两者之间的显著性差异。

它的公式如下：t= (X1 - X2) / s√(1/n1 + 1/n2)其中，X1和X2表示两个样本的平均值；s表示两个样本的标准差；n1和n2表示两个样本的样本量。

z检验是一种多比较检验，也就是说，它可以用来比较多个组之间的差异。

它的公式是：z= (X1 -X2 - ... - Xk) / s(1/n1 + 1/n2 + ... + 1/nk) 其中，X1、X2、…、Xk表示多个样本的平均值；s表示多个样本的标准差；n1、n2、…、nk表示多个样本的样本量。

卡方检验是一种进行多个组之间的差异检验的方法，卡方检验的公式是：χ2= [∑(O1 - E1)2 / E1] + [∑(O2 - E2)2 / E2] + ... + [∑(Ok - Ek)2 / Ek]其中，O1、O2、…、Ok表示多个样本的实际值；E1、E2、…、Ek表示多个样本的期望值。

上述就是显著性差异计算公式的简要介绍。

它们都是用来测量两个或多个样本之间的显著性差异的方法，比较不同样本之间的关系。

显著性差异计算公式在统计领域有着广泛的应用，它可以用来检验某个指标在不同组别之间和不同时期之间的变化和变化趋势是否具有显著性。

例如，可以用来测定某件事被改变后，人们对它的反应是否具有显著性，或者是否有两个商品之间的差异具有显著性。