用法向量求二面角的大小

立体几何二面角的求法立体几何是数学的一个重要分支，研究的是空间中的图形和其性质。

其中，二面角是立体几何中的一个重要概念，它是由两个平面所围成的角。

本文将介绍二面角的定义、性质以及求法。

一、二面角的定义二面角是由两个平面所围成的角，其中一个平面称为顶面，另一个平面称为底面，二面角的两个边分别位于顶面和底面上。

二面角常用字母α表示。

二、二面角的性质1. 二面角的大小是以顶点为中心，两个边所围成的平面角的大小，即α=∠POQ。

2. 二面角的大小是由顶面和底面的位置关系决定的，与边的长度无关。

3. 二面角的度量范围是0到180度。

4. 如果两个平面平行，则它们所围成的二面角为0度。

5. 如果两个平面相互垂直，则它们所围成的二面角为90度。

6. 如果两个平面相交于一条直线，则它们所围成的二面角为180度。

三、二面角的求法1. 通过向量法求解二面角：设顶面的法向量为n1，底面的法向量为n2，二面角的余弦值可以通过两个法向量的点乘公式求解：cosα=n1·n2/(|n1||n2|)，其中·表示点乘，|n1|和|n2|分别表示n1和n2的模。

2. 通过平面法向量求解二面角：设顶面的法向量为n1，底面的法向量为n2，二面角的余弦值等于两个法向量的模的乘积与它们的点乘的商：cosα=(|n1|·|n2|)/(n1·n2)。

3. 通过平面方程求解二面角：设顶面的平面方程为Ax+By+Cz+D1=0，底面的平面方程为Ax+By+Cz+D2=0，二面角的余弦值等于两个平面方程的D1、D2的差值与它们的模的乘积的商：cosα=(D1-D2)/(√(A^2+B^2+C^2)·√(A^2+B^2+C^2))。

四、二面角的应用1. 二面角常用于计算空间中的体积和表面积。

2. 在物理学中，二面角常用于描述力的方向和大小。

3. 在几何光学中，二面角常用于计算光的反射和折射。

4. 在工程中，二面角常用于计算材料的强度和稳定性。

用法向量确定二面角大小的三个基本关系作者：程映军来源：《甘肃教育》2012年第23期〔关键词〕数学教学；法向量；二面角；符号；方向；相关关系〔中图分类号〕 G633.65 〔文献标识码〕 A〔文章编号〕 1004—0463（2012）23—0082—02求二面角平面角的问题在传统立体几何中解决的方法较多，这也是高考的一个重要内容，但新教材对此问题有所淡化，只要求学生能用平面法向量求出二面角平面角的大小.而两个法向量的夹角与二面角的平面角到底何时相等？何时互补？教材中处理得比较含糊，要求借助于图形直观解决，实际上此法可操作性并不大，因此，到了这个部分便常常出现“老师想讲讲不清，学生能学学不透”的尴尬局面.那么，如何在判断方法上兼顾理论依据的正确性和事件操作的可行性、简捷性呢？笔者认为，只要认识清楚以下三个基本关系，我们并不需要借助其他理论工具，就能快速解决这一问题.一、空间向量坐标的符号与向量方向的关系一个向量的坐标并不是刻画这个向量在空间直角坐标系O-xyz中的具体位置，而是刻画向量相对于标准正交基[i][➝]=（1，0，0），[j][➝]=（0，1，0），[k][➝]=（0，0，1）的“分解程度”.如，将向量[m][➝]=（x，y，z）分解，则此向量在x轴、y轴、z轴上的分向量依次是=（x，0，0）=x[i][➝]，=（0，y，0）=y[j][➝]，=（0，0，z）=z[k][➝]，从而x，y，z的正负直接反映这三个分向量与对应的基底是同向还是反向，如下表：二、平面法向量的横、纵、竖之间的相关关系平面α的法向量的坐标之间构成正比例关系.证明：设A0（x0，y0，z0），A1（x1，y1，z1），A2（x2，y2，z2）是平面α上任意三个不共线的点，[m][➝]=（x，y，z）是平面α的法向量，则[m][➝]⊥[m][➝]⊥⇒[m][➝]·=0[m][➝]·=0⇒x（x1-x0）+y（y1-y0）+z（z1-z0）=0x（x2-x0）+y（y2-y0）+z（z2-z0）=0 ，解得y=-x，z=-xy1-y0 z1-z0y2-y0 z2-z0 ≠0. 记λ1=-，μ1=-，则[m][➝]=（x，λ1x，μ1x）=x（1，λ1，μ1）；同理，λ2=-，μ2=-x1-x0 z1-z0x2-x0 z2-z0 ≠0，则[m][➝]=（λ2y，y，μ2y）=y（λ2，1，μ2）；令λ3=-，μ3=-x1-x0 y1-y0x2-x0 y2-y0 ≠0，则[m][➝]=（λ3z，μ3z，z）=z（λ3，μ3，1）.这说明，由A0，A1，A2三点唯一确定的平面α，其法向量可以由x（或y，z）唯一确定.三、二面角的大小与两个法向量相对指向的关系定义1：以l为棱的两个半平面α，β把空间分成两部分，其中使二面角α-l-β的平面角θ∈（0，π）的部分称为二面角的内部，另一部分则称为二面角的外部.定义2：以平面α上任意一个不属于棱的点为起点作该平面的法向量，如果这个法向量的终点总是落在二面角α-l-β的外部，则称该法向量指向二面角α-l-β的外部，反之，称该法向量指向二面角α-l-β的内部.有以下事实：①当α，β的法向量[m][➝]，[n][➝]同时指向二面角α-l-β的内部（或外部）时，角与二面角α-l-β互为补角（图1）.②当α，β的法向量[m][➝]，[n][➝]一个指向二面角α-l-β的内部，另一个指向二面角α-l-β的外部时，角与二面角α-l-β大小相等（图2）.对于以上三个基本关系的阐述和证明，我们可以看到，要解决提出的问题，关键是要判断两个法向量的相对方向.而由于平面法向量的方向可以通过点坐标的行列式运算化归为一元线性表达式，所以我们只需要判断出平面法向量的任意一个坐标的符号，就可以确定法向量的相对方向，从而判断出两个法向量夹角与二面角的大小关系，实现整个问题的求解.以下举例说明该方法的具体实施过程.例1：如图3，已知平面A1B1C1平行于三棱锥V-ABC的底面ABC，等边△AB1C所在的平面与底面ABC垂直，且∠ACB=90°，设AC=2a，BC=a.（1）求证直线B1C1是异面直线AB1与A1C1的公垂线；（2）求点A到平面VBC的距离；（3）求二面角A-VB-C的大小.解析：（1）（2）略.（3）取AC中点O，连接B1O，易知OB1⊥底面ABC，过O作直线OE∥BC交AB于E.取O为空间直角坐标系的原点，以OE，OC，OB1所在直线分别为x轴，y轴，z轴建立如图4所示的空间直角坐标系.则A（0，-a，0），B（a，a，0），C（0，a，0），B1（0，0，a）.设平面VBC的一个法向量[n][➝]=（x1，y1，z1），由[n][➝]⊥[n][➝]⊥得-ax1=0-ay1+az1=0，取z1=1，得[n][➝]=（0，，1），此时法向量[n][➝]指向二面角A-VB-C的外侧.同理可得平面VAB的一个法向量[m][➝]=（2，-，1），此时，法向量[m][➝]指向二面角A-VB-C的内侧.∴cos==-.所以，二面角A-VB-C的大小为arccos-.例2：在正方体中，二面角的大小为 .解：如图5，A1C1⊥面BB1D1，A1D⊥面BAD1，所以直线A1C，A1D的方向向量分别为BB1D1和BAD1的法向量，分别令[n1][➝]=，[n2][➝]=，设正方形的边长为1，建立如图所示的空间直角坐标系，则A1（0，1，1）， C1（-1，0，1），D1（-1，-1，0）.∴ =（-1，-1，0）， ||= ， =（-1，-2，-1），||=， ·=3.∴cos==.即向量，的夹角为30°，由于，的指向都是向着二面角外，所以二面角A-BD1-B1与向量，的夹角互补，所以二面角A-BD1-B1的大小为150°.。

求二面角的六种方法求解二面角是空间几何学中常见的问题，它在多个领域如物理学、化学和工程学中都有广泛的应用。

本文将介绍六种求解二面角的方法，包括向量法、坐标法、三角法、平面几何法、球面几何法和投影法。

一、向量法向量法是一种简便的求解二面角的方法。

它利用向量的夹角来表示二面角。

首先，我们需要确定两个平面的法向量，然后计算它们之间的夹角。

通过向量的点积和模长运算，可以得到二面角的大小。

二、坐标法坐标法是一种常用的求解二面角的方法。

它利用坐标系中的点来表示二面角。

我们可以通过给定的坐标点，计算两个平面的法向量，然后利用向量夹角的公式求解二面角。

三、三角法三角法是一种基于三角函数的求解二面角的方法。

它利用三角函数的性质来计算二面角的大小。

通过已知的边长和角度，可以利用正弦定理、余弦定理等公式求解二面角。

四、平面几何法平面几何法是一种利用平面几何关系求解二面角的方法。

它通过已知的平面形状和角度关系，利用平面几何的知识来求解二面角的大小。

例如，可以利用平行线的性质、垂直线的性质等来计算二面角。

五、球面几何法球面几何法是一种利用球面几何关系求解二面角的方法。

它通过已知的球面形状和角度关系，利用球面几何的知识来求解二面角的大小。

例如，可以利用球面上的弧长、球面上的角度等来计算二面角。

六、投影法投影法是一种利用投影关系求解二面角的方法。

它通过已知的投影长度和角度关系，利用投影几何的知识来求解二面角的大小。

例如，可以利用平面上的投影线段、平面上的角度等来计算二面角。

通过以上六种方法，我们可以灵活地求解二面角的大小。

不同的问题和场景可能适用不同的方法，我们可以根据具体情况选择合适的方法来解决问题。

这些方法在实际应用中具有重要的意义，能够帮助我们更好地理解和解决相关问题。

总结起来，求解二面角的六种方法分别是向量法、坐标法、三角法、平面几何法、球面几何法和投影法。

每种方法都有其特点和适用场景，我们可以根据具体问题选择合适的方法来求解二面角。

高中数学求二面角技巧
高中数学中，求解二面角是一项重要的技巧。

二面角是指两个平面相交而形成的角度，常常出现在几何题目中。

以下是一些求解二面角的技巧：
1. 使用向量法求解二面角
向量法是求解二面角的常用方法。

假设有两个平面AB和CD，且它们相交于一条直线EF。

设向量AB=n，向量CD=m，向量EF=a，则二面角θ的余弦值为：
cosθ=(n·m)/( |n|·|m| )
其中，n·m表示n和m的数量积，|n|和|m|表示向量n和向量m 的模长。

2. 利用三角函数求解二面角
如果已知二面角的两个面的斜率，可以使用三角函数求解二面角。

设两个平面的斜率分别为k1和k2，则二面角的正切值为：
tanθ=(k1-k2)/(1+k1k2)
可以使用反正切函数求解出二面角的值。

3. 利用平面几何知识求解二面角
通过平面几何知识，可以求解出两个平面的交线与一个球面的交线，从而求解二面角。

设两个平面在点O处相交，交线为AB和CD，球心为O，球面与交线AB和CD的交点分别为P和Q，则二面角θ等
于∠POQ。

以上是求解二面角的一些常用技巧，希望对高中数学学习有所帮
助。

用法向量求二面角的大小及其角度关系的确定我们都知道，向量知识在数学学科里有其非常广泛的应用，尤其是在立体几何求角和距离时，若利用向量知识求解会得到事半功倍的效果，也正体现了向量知识的工具性和灵活性。

而在应用向量知识求解二面角的大小时，不是所有的二面角的两个半平面的法向量的夹角都和二面角相等，有时是互补，那么，什么时候相等，什么时候互补，如何确定其“角度之间的大小关系”一直以来是困扰很多教师和学生的一个难题。

向量有其自身的独特性质—自由性，当一个向量在空间的某一位置时，可以自由移动，只要满足其方向不变，其无论移动到任何位置，向量都是相等的。

根据这一性质，当我们把二面角的某个半平面的法向量求出后，把它的起点放到坐标原点，然后确定其向量的方向的指向，从而确定其法向量的夹角和二面角的大小的关系，在确定了法向量的夹角与二面角的关系后，再利用向量的数量积求出二面角的大小，下面就来具体阐述一下这一做法。

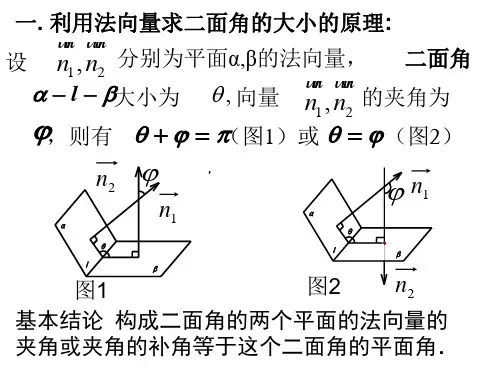
一．规定法向量的指向方向1.当法向量的方向指向二面角的内部时称之为向里指，如：图1中的向量。

2.当法向量的方向指向二面角的外部时称之为向外指，如：图1中的向量。

二．法向量的夹角和二面角大小的关系1.设分别为平面的法向量，二面角的大小为，向量的夹角为，当两个法向量的方向都向里或都向外指时，则有（图2）；2.当两个法向量的方向一个向里指一个向外指时（图3）图2图3三、在坐标系中做出法向量，从而确定法向量的方向指向1.已知二面角，若平面的法向量，由向量的相等条件知，坐标是（4，4，3）的向量有无数多个，根据向量的自由性，我们只需做出由原点出发的一个向量便可，如图4所示，从而，我们很容易的判断出平面法向量的方向的指向，是指向二面角的里面。

2.若平面法向量，同理可做出从原点出发的法向量，如图5所示，显然，方向是指向二面角的外面。

四．应用举例例题1. 如图6，在棱长为1的正方体ABCD-A1B!C1D1中G、E、F分别为AA1、AB、BC的中点，求作二面角G—EF—D半平面GEF的法向量并判断其方向。

用向量求二面角的四种方法
作者：林明成
来源：《数理化学习·高三版》2008年第12期
向量法求二面角是一种独特的方法，因为它不仅是对传统方法的有力补充，而且还可以最大限度地避开思维的高强度转换和各种辅助线添加的困难，将灵活的逻辑推理转化为机械的代数运算.它降低了问题的难度，简缩了思维的过程，可操作性强.但在具体运用过程中也需针对具体问题采用不同的转化方式.
一、借助空间向量基本定理和向量夹角公式
例1 如图1，四边形ABCD是直角梯形，∠ABC=90°，SA⊥平面ABCD，
SA=AB=BC=1，AD=1/2，求平面SCD与平面SAB所成锐角二面角的大小.。