六年级数学几何图形知识点归纳结构图
- 格式:docx
- 大小:505.35 KB
- 文档页数:1


一、《知识要点》多边形:由一些不在同一条直线上的线段依次首尾相连组成的封闭平面图形。
设一个多边形的边数为n(n≥3,且n 为整数),从一个顶点出发的对角线有(n-3)条;可以把n 边形成(n-2)个三角形;这个n 边形共有2)3( n n 条对角线。
注意:凸多边形和凹多边形都属于多边形。
有弧或不封闭图形都不是多边形。
扇形:(弧:圆上A 、B 两点之间的部分叫做弧。
)由一条弧和经过这条弧的端点的两条半径所组成的图形叫做扇形。
三视图:从正面看到的图,叫做主视图。
左视图:从左面看到的图,叫做左视图。
俯视图:从上面看到的图,叫做俯视图。
截一个正方体:用一个平面去截一个正方体,截出的面可能是三角形,四边形,五边形,六边形。
★总结:截一个几何体,这个几何体有几个平面就能截出几边形。
欧拉公式:f+v-e=2. f 为一个多面体的顶点数,v 表示面数,e 表示棱数。
1、正方体:(1)六个面(全部相等);八个顶点;十二条棱(全部相等)。
(2)展开图:第一类1,4,1,中间四连方,两侧各一个,共六种。
第二类:2,3,1或者1,3,2中间三连方,两侧各有一、二个,共三种。
第三类:2,2,2中间二连方,两侧各有二个,只有一种。
第四类:3,3两排各三个,只有一种(2)将一个正方体(或者长方体或四棱柱)用剪刀剪开,至少需要剪几下:7刀,顶面三条棱剪开,底面相应的那三条棱也剪开,侧面剪开一条2.长方体:六个面(不相同),八个顶点,十二条棱(四条侧棱相等)可以截出的图形与正方体相同 展开:举一例:3、圆柱体:三个面(两个圆,一个曲面),没有顶点;可以截出圆,长方形;展开侧面是长方形,两个底面是圆(图1)。
4、圆锥体:两面(一个曲面和一个圆),一个顶点。
能截出圆、三角形。
展开是一个扇形和一个圆(图2) 5、棱柱体:(棱最少的棱柱是三棱柱)顶面(或者底面)有几条棱就叫做几棱柱。
n 棱柱有3n 条棱,2n 个顶点,n+2个面,正n棱柱,每个侧面相等,每条侧棱相等,两个底面相等。


六年级圆的知识点归纳圆是我们数学学习中重要的几何图形之一,它在日常生活和工作中都有广泛的应用。
在六年级,我们学习了很多关于圆的知识点,包括圆的定义、圆的性质、圆的元素等等。
下面就让我们来归纳总结一下六年级圆的知识点。
一、圆的定义圆是平面上距离一个确定点的距离都相等的点的轨迹。
其中,这个确定点叫作圆心,到圆心的距离叫作半径,通过圆心的两个点叫作直径。
圆的定义是我们学习圆的基础。
二、圆的性质1. 圆的直径是圆上最长的线段,它的两个端点就是圆的两个点。
圆的直径等于两倍的半径。
2. 圆的半径相等的两段弧所对应的圆心角也相等。
3. 圆的半径垂直于所对应的弧上的弦,且平分弦。
4. 在圆上,所有的半径都相等。
5. 圆的弦和半径的关系为:圆的弦长等于两倍半径与该弦所对应的圆心角的正弦值的乘积。
6. 圆上的切线垂直于半径。
三、圆的元素一个圆主要包括圆心、半径、直径、切点、切线以及弧等元素。
1. 圆心:圆心是圆的中心点,通常用字母O表示。
2. 半径:半径是圆心到圆上任意一点的距离,通常用字母r表示。
3. 直径:直径是通过圆心并且两端都在圆上的线段,直径等于半径的两倍,通常用字母d表示。
4. 切点:切点是切线与圆相交的点,切点位于圆上。
四、圆的计算在解决一些与圆相关的问题时,我们需要进行一些计算。
1. 周长:圆的周长是圆上一圈的长度,计算公式为C = πd ,其中 d 是圆的直径,π 是一个近似值,约等于3.14。
2. 面积:圆的面积是圆所包含的平面区域的大小,计算公式为A = πr² ,其中 r 是圆的半径。
五、圆的应用圆在日常生活和工作中有广泛的应用。
1. 圆形的车轮,使汽车能够平稳地行驶。
2. 圆形的饼干、饼干夹心,给我们带来美味。
3. 圆形的钟表,帮助我们掌握时间。
4. 圆形的邮票、硬币,是经常使用的物品。
5. 圆形的几何图形中,各个知识点的应用,如计算圆的面积、解决与圆相关的问题等等。
六年级圆的知识点归纳就是上述这些内容,通过学习和理解这些知识,我们能够更好地应用圆的知识解决实际问题,并且拓展我们的数学思维。

圆规是数学几何中常见的工具之一,用于绘制和测量圆的各种属性。
下面是六年级圆规知识点的归纳:1.圆规的结构和使用方法:-圆规由固定的一只脚和可移动的一只脚组成,可移动脚上有一个锋利的笔尖或铅笔芯。
-圆规的固定脚上有一个可调节的刻度盘,用于测量圆的半径或直径。
-使用圆规时,应将固定脚放在画纸上,通过调节刻度盘使可移动脚与固定脚相切或相交,然后绘制所需要的线条。
2.圆的基本概念:-圆是由平面上任意一点到固定点的距离保持不变的点的集合。
-圆心是固定的点,圆心到圆上任意一点的距离称为半径,用字母r表示。
-直径是圆上任意两点之间通过圆心的线段,直径的长度为半径的两倍。
3.圆的相关性质:-圆的任意一条直径都将圆分为两个等分的半圆。
-圆的两条直径垂直相交。
-圆的半径相等。
-圆的半径垂直于其所在的切线。
4.利用圆规绘制圆的方法:-绘制半径:将圆规的可移动脚与固定脚相切于圆心,然后调整刻度盘的值,使可移动脚到达所需的半径长度,最后绘制半径线。
-绘制直径:将圆规的可移动脚与固定脚相交于圆心,然后调整刻度盘的值,使可移动脚到达所需的直径长度,最后绘制直径线。
-绘制切线:将圆规的可移动脚与固定脚相切于圆上一点,然后将可移动脚旋转一定角度,使可移动脚到达切线与圆的交点,最后绘制切线。
5.圆的计算:-计算圆的周长:圆的周长等于直径的长度乘以π(π≈3.14),即公式C=πd或C=2πr。
-计算圆的面积:圆的面积等于半径的平方乘以π,即公式A=πr²。
6.圆与其他几何图形的关系:-圆与正方形:正方形的对角线等于边长的√2倍,而圆的直径等于半径的2倍,因此正方形的对角线长度等于圆的直径的长度。
-圆与三角形:圆心到三角形的三个顶点的距离相等时,这个三角形是等边三角形,等边三角形的外接圆的圆心就是三角形的重心。

六年级数学上册必背知识一、圆的知识1、圆是由曲线围成的平面封闭图形。
圆中心的一点叫圆心,用字母O 表示。
以某一点为圆心,可以画无数个圆。
连接圆心和圆上任意一点的线段叫半径,用字母r 表示。
连接圆心并且两端都在圆上的线段叫直径,用字母d 表示。
2、圆有无数条半径,有无数条直径。
圆心决定圆的位置,半径决定圆的大小。
3、在同一个圆中,所有的半径都相等,所有的直径都相等。
在同一个圆中,直径是半径的2倍,半径是直径的12。
4、车轮为什么是圆的?答:因为圆心到圆上各点的距离相等,所以圆在滚动时,圆心在一条直线上运动,这样的车轮运行才稳定。
5、圆内最长的线段是直径,圆规两脚之间的距离是半径。
6、在一个正方形里画一个最大的圆,圆的直径就是正方形的边长。
在一个长方形里画一个最大的圆,圆的直径就是长方形的宽。
7、把圆对折,再对折(对折2次)就能找到圆心。
因此,圆是轴对称图形,直径所在的直线是圆的对称轴,圆有无数条对称轴。
半圆只有1条对称轴。
8、如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴,这时,我们也说这个图形关于这条直线的轴对称。
对称轴是一条直线。
9、常见的轴对称图形:等腰三角形(1条)、等边三角形(3条)、等腰梯形(1条)、长方形(2条)、正方形(4条)、圆(无数条)、半圆(1条)。
10、圆一周的长度就是圆的周长。
圆的周长总是直径的3倍多一些,圆的周长除以直径的商(圆的周长与直径的比值)是一个固定的数,我们把它叫做圆周率,用字母π表示, π是一个无限不循环小数,为了计算简便,通常取近似值3.14。
11、圆的周长=圆周率×直径 即 C 圆=πd =2πr 。
12、圆所占平面的大小叫圆的面积。
把圆等分的份数越多,拼成的图形就越接近平行四边形或长方形。
拼成的平行四边形的底相当于圆周长的一半,高相当于圆的半径;长方形的长相当于圆周长的一半,宽相当于圆的半径。
13、如果用S 表示圆的面积, r 表示圆的半径,那么圆的面积公式:S 圆=πr 2 。



六年级圆的知识点归纳总结在六年级的数学学习中,圆是一个重要的几何形状。
下面是对圆的知识点的归纳总结。
1. 圆的基本概念圆是由平面上离一个固定点距离都相等的点的集合组成的几何图形。
这个固定点称为圆心,而到圆心距离相等的线段称为半径。
半径的两个端点就是圆上的点,我们称之为圆上的点。
圆的边界称为圆周。
2. 圆的元素和符号圆的元素包括:圆心、半径、直径、圆弧、扇形和弦等。
圆心用“O”表示,半径用“r”表示,直径用“d”表示。
圆弧是圆周上的一段弧,它的两个端点和圆心确定了一个角,叫做圆心角。
扇形是由圆心、圆周上一段圆弧以及圆弧两端所对的弦组成的图形。
3. 圆的性质(1) 圆的半径相等性质:圆周上的所有半径都相等。
(2) 圆的直径性质:直径是圆中最长的一条弦,它的长度等于半径的两倍,可以通过圆心连接圆周上的两点得到。
(3) 圆的弦性质:圆上的任意一条弦都小于等于直径的长度,等于直径的弦是直径本身。
(4) 圆的弧性质:圆上的两个弧等于它们所对的圆心角的一半。
(5) 圆的周长性质:圆的周长等于直径乘以π (圆周率)。
4. 圆的计算公式(1) 圆的周长公式:C = 2πr,其中C表示圆的周长,r表示半径。
(2) 圆的面积公式:A = πr²,其中A表示圆的面积,r表示半径。
5. 圆的应用圆是几何学中的基本形状,广泛应用于各个领域。
以下是一些圆的应用示例:(1) 圆形物体的计算:计算圆形饼干、蛋糕等的面积和周长。
(2) 圆形运动:描述物体在一个固定圆心旋转的轨迹。
(3) 圆形体育器材:例如篮球、足球等球形器材。
(4) 圆形建筑:例如圆形舞台、圆形建筑物等。
以上是对六年级圆的知识点的归纳总结。
通过对圆的基本概念、元素与符号、性质、计算公式以及应用的了解,可以更好地掌握圆的相关知识,提高数学学习的效果。
在实际生活中,圆的概念和性质的应用也非常广泛,能够帮助我们更好地理解和利用它们。

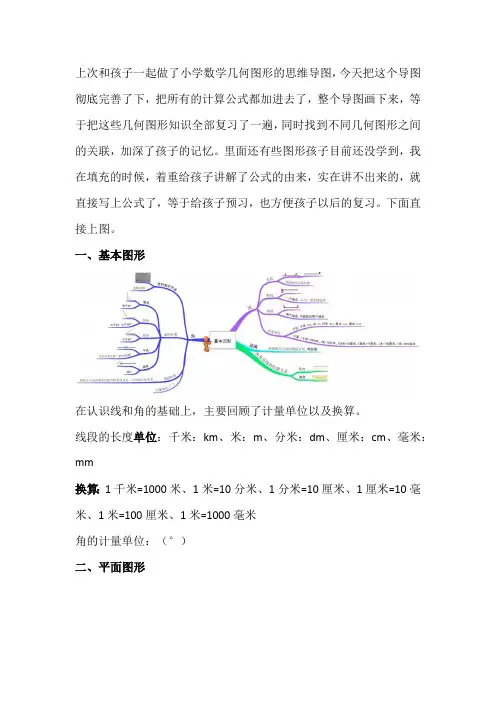
上次和孩子一起做了小学数学几何图形的思维导图,今天把这个导图彻底完善了下,把所有的计算公式都加进去了,整个导图画下来,等于把这些几何图形知识全部复习了一遍,同时找到不同几何图形之间的关联,加深了孩子的记忆。
里面还有些图形孩子目前还没学到,我在填充的时候,着重给孩子讲解了公式的由来,实在讲不出来的,就直接写上公式了,等于给孩子预习,也方便孩子以后的复习。
下面直接上图。
一、基本图形在认识线和角的基础上,主要回顾了计量单位以及换算。
线段的长度单位:千米:km、米:m、分米:dm、厘米:cm、毫米:mm换算:1千米=1000米、1米=10分米、1分米=10厘米、1厘米=10毫米、1米=100厘米、1米=1000毫米角的计量单位:(°)二、平面图形平面图形在认识三角形、四边形、圆的基础上,主要是回顾计量单位、周长、面积计算公式,还有些图形对应的性质。
面积的计量单位:1、周长:围成一个图形的所有边长的总和就是这个图形的周长周长的计量单位和换算和线段一样2、面积:物体的表面或围成的平面图形的大小,叫做它们的面积面积的计量单位:平方千米、公顷、平方米、平方分米、平方厘米单位换算:1平方千米=100公顷、1公顷=10000平方米、1平方米=100平方分米、1平方分米=100平方厘米长方形:周长:长方形周长=(长+宽)× 2面积:长方形面积=长×宽正方形:正方形周长= 边长× 4正方形面积= 边长×边长长方形和正方形的周长和面积公式,孩子都记得比较熟悉,所以直接列出来。
平行四边形:平行四边形的周长是四条边相加,但对边相等,所以只要是两条边相加×2就可以了。
面积:平行四边形的面积是通过剪切和平移,转化成一个长方形来计算,最后演变结果是:平行四边形面积=底×高。
即:S=ah梯形:周长比较好计算,四边相加即可。
梯形的面积演变过程,因为两个一样的梯形可以拼成一个平行四边形,所以梯形的面积就是:梯形面积=(上底+下底)×高÷2。
六年级的几何知识点在小学六年级的数学学习中,几何知识点是非常重要的一部分。
通过学习几何,孩子们可以培养空间想象力和逻辑思维能力,提高解决问题的能力。
下面是六年级学习的几何知识点的整理:1.图形的分类在几何学中,图形是一个重要的概念。
六年级学生需要学会识别和分类各种图形。
常见的图形包括三角形、四边形、五边形、六边形等。
他们需要了解这些图形的定义和特点,如三角形有三条边、三个角等。
2.平面和立体图形除了学习分类不同形状的图形外,六年级学生还需要了解平面和立体图形的概念。
平面图形是指只有长、宽两个维度的图形,如正方形、圆形等,而立体图形是有长度、宽度和高度三个维度的图形,如立方体、正金字塔等。
3.对称和相似在六年级学习几何时,对称和相似两个概念也是需要重点掌握的。
对称是指一个图形可以通过某个轴线对折后完全重合,如正方形和长方形都具有对称性。
相似则是指两个图形形状相似,但大小不一样,其中一个是另一个的缩放。
学生需要学会判断图形是否对称和相似,并能够找到相似的图形对应的边和角。
4.三角形的性质六年级学生在几何学习中还需要熟悉三角形的性质。
三角形包括等腰三角形、等边三角形等,学生需要了解它们的定义和特点。
例如,等腰三角形具有两边相等,等边三角形的三边都相等。
5.四边形的性质学生还需要了解四边形的性质。
常见的四边形包括正方形、长方形、菱形等。
学生需要掌握它们的特点,如正方形的四条边相等、长方形的对角线相等等。
6.角的概念和性质角是几何学中另一个重要的概念。
六年级学生需要了解角的定义和性质。
他们需要知道角由两条射线构成,可以通过角度的大小来分类,如锐角、直角和钝角。
7.平移、旋转和翻转在几何学中,平移、旋转和翻转是一些基本的变换方式。
学生需要学会通过平移、旋转和翻转改变图形的位置和方向。
这些变换有助于他们理解空间关系和几何图形的属性。
通过学习以上几何知识点,六年级的学生可以培养良好的观察和思维能力,提高解决几何问题的能力。
六年级圆扇形知识点归纳圆扇形是数学中的一个重要概念,它是由圆心、半径和一段弧所围成的一部分区域。
在六年级数学中,我们学习了许多关于圆扇形的知识点,包括面积、周长以及与其它几何图形的关系。
在本文中,我将对这些知识点进行详细的介绍和归纳。
1. 圆扇形的定义与性质:圆扇形是由一段弧和两条半径所围成的区域。
圆心是圆扇形的一个重要要素,它与圆上的任意一点之间的线段都是半径。
另外,圆扇形的弧长等于圆周长的一部分,圆扇形的中心角等于所对的弧的两个半径之间的夹角。
2. 圆扇形的面积计算:圆扇形的面积可以通过弧长和半径计算得到。
设圆扇形的半径为r,中心角为θ,弧长为s,则圆扇形的面积可以表示为:S = (θ/360) * π * r^2,其中π是一个常数,约等于3.14159。
这个公式可以帮助我们准确地计算圆扇形的面积。
3. 圆扇形的周长计算:圆扇形的周长是指沿着圆弧的长度加上两条半径的长度之和。
如果我们知道圆扇形的半径和中心角,就可以通过以下公式计算圆扇形的周长:C = 2πr * (θ/360),其中C表示圆扇形的周长,r是半径,θ是中心角。
4. 圆扇形与其他几何图形的关系:圆扇形与其他几何图形之间存在一些有意思的关系。
例如,圆扇形可以看作是一个三角形与一个圆形相结合的图形。
三角形的底边是圆扇形的弧,而两条直角边则是圆扇形的两条半径。
另外,圆扇形还与扇形、圆环、圆柱体等图形的计算有一定的联系,可以通过转化为这些图形的计算问题来求解圆扇形的面积和周长。
5. 圆扇形的应用:圆扇形的概念在真实生活中有许多应用。
例如,在扇形花坛的设计中,我们可以根据圆扇形的面积和周长来计算需要多少土壤和种子。
此外,圆扇形的概念还在音响、舞台灯光设计等领域得到广泛应用。
通过合理地布置扇形区域,可以达到更好的声音扩散和光线聚焦效果。
综上所述,六年级学生应该掌握圆扇形的基本概念、性质以及计算方法。
通过理解和应用这些知识点,我们可以更好地理解几何图形的特性,并且在实际问题中灵活运用。
图形与几何一线和角(1)线* 直线直线没有端点;长度无限;过一点可以画无数条,过两点只能画一条直线。
* 射线射线只有一个端点;长度无限。
* 线段线段有两个端点,它是直线的一部分;长度有限;两点的连线中,线段为最短。
* 平行线在同一平面内,不相交的两条直线叫做平行线。
两条平行线之间的垂线长度都相等。
* 垂线两条直线相交成直角时,这两条直线叫做互相垂直,其中一条直线叫做另一条直线的垂线,相交的点叫做垂足。
从直线外一点到这条直线所画的垂线的长叫做这点到直线的距离。
(2)角(1)从一点引出两条射线,所组成的图形叫做角。
这个点叫做角的顶点,这两条射线叫做角的边。
(2)角的分类锐角:小于90°的角叫做锐角。
直角:等于90°的角叫做直角。
钝角:大于90°而小于180°的角叫做钝角。
平角:角的两边成一条直线,这时所组成的角叫做平角。
平角180°。
周角:角的一边旋转一周,与另一边重合。
周角是360°。
二平面图形1长方形(1)特征对边相等,4个角都是直角的四边形。
有两条对称轴。
(2)计算公式c=2(a+b) s=ab2正方形(1)特征:四条边都相等,四个角都是直角的四边形。
有4条对称轴。
(2)计算公式c= 4as=a23三角形(1)特征由三条线段围成的图形。
内角和是180度。
三角形具有稳定性。
三角形有三条高。
(2)计算公式s=ah/2(3)分类按角分锐角三角形:三个角都是锐角。
直角三角形:有一个角是直角。
等腰三角形的两个锐角各为45度,它有一条对称轴。
钝角三角形:有一个角是钝角。
按边分不等边三角形:三条边长度不相等。
等腰三角形:有两条边长度相等;两个底角相等;有一条对称轴。
等边三角形:三条边长度都相等;三个内角都是60度;有三条对称轴。
4平行四边形(1)特征两组对边分别平行的四边形。
相对的边平行且相等。
对角相等,相邻的两个角的度数之和为180度。
平行四边形容易变形。
2023-2024学年期末核心考点集训专题讲义专题07:图形与几何——图形的认识与测量考点01 直线、射线、线段考点02 角的认识考点03立体图形的认识考点04 平面图形的测量考点05立体图形的测量考点01 比的概念知识点一:直线、射线 、线段【例题1】过一点可以画几条直线?过两点可以画几条直线?答:过一点可以画无数条直线,过两点可以画一条直线。
下面线段表示的是0°到180°,点A、B、C、D中,与钟面上时针和分针所形成的较小角的度数最接近的是点()。
考点02 角知识点一:角的认识1.从一点引出两条射线组成的图形叫作角。
2.角的大小与两边的长短无关,与角张开的大小有关。
知识点二:角的分类知识点三:三角形1.由三条线段首尾相连围成的封闭图形是三角形。
每个三角形都有3个顶点、3条边、3个角。
2.从三角形的一个顶点向它的对边作一条垂线,顶点和垂足之间的线段叫作三角形的高。
任意三角形都有三条高。
3.三角形的分类4.四边形5.圆在一个平面内,一动点以一定点为中心,以一定长度为距离旋转一周,所形成的封闭图形就是圆。
【例题1】一个直角三角形的两个锐角的和是多少度?为什么?答:一个直角三角形的两个锐角的和是90°。
因为三角形内角和为180°,180°减去直角90°,就是两个锐角的和90°。
一个三角形三个内角的度数比是2∶3∶5,这个三角形是 ()三角形考点03 立体图形的认识知识点一:长方体、正方体特征知识点二:圆柱、圆锥知识点三:长方体、正方体、圆锥展开图下面是琳琳从不同方向观察一个几何体看到的图形,这个几何体是( C )。
如图,一个立体图形由五个同样大小的组成,如果再摆一个,要使其从右面看到的图形不变,有()种摆法。
(面与面相接)考点04 平面图形的测量知识点一:平面图形的面积计算平面图形的面积计算公式长方形的面积一长X宽用数方格的方法推导。
一到六年级图形知识点总结归纳图形是数学中的一个重要概念,通过研究和学习图形可以帮助我们提高空间思维和几何理解能力。
在一到六年级的数学教育中,学生需要逐渐学习和掌握不同类型图形的性质、特点和应用。
以下是一到六年级图形知识点的总结归纳。
一年级图形知识点:1. 点:点是图形的基本单位,没有大小和形状。
2. 线段:由两个端点确定的部分,没有宽度和厚度。
3. 直线:无限延伸的线段,没有端点。
4. 封闭图形:由线段组成的图形,边界形成一个闭合的曲线。
二年级图形知识点:1. 正方形:四条边相等、四个顶点呈直角的四边形。
2. 长方形:相对边长度相等、四个顶点呈直角的四边形。
3. 圆形:由一个固定点到其它所有点的距离都相等的平面图形。
4. 三角形:有三条边和三个顶点的图形。
5. 直角三角形:一个内角为直角(90度)的三角形。
三年级图形知识点:1. 平行线:在同一个平面中,永不相交的直线。
2. 垂直线:两条相交直线的内角互为直角(90度)。
3. 梯形:至少有一对平行边的四边形。
4. 菱形:四条边长度相等的凸四边形。
5. 钝角:大于直角小于平角(180度)的角度。
四年级图形知识点:1. 曲线:非直线的线段。
2. 多边形:有多条直线边的封闭图形。
3. 正多边形:具有相等边长且内角相等的多边形。
4. 条形图:通过长方形的面积表示数据分布的图形。
5. 饼图:通过圆形的扇区面积表示数据比例的图形。
五年级图形知识点:1. 锐角:大于0度小于直角的角度。
2. 二维图形与三维图形的转换:平面图形的展开与折叠,以及在三维空间中的展示。
3. 矩形:具有相对边相等且内角为直角的四边形。
4. 圆柱体:由一个圆形和一个与该圆共面的矩形构成的立体图形。
六年级图形知识点:1. 平行四边形:具有两对平行边的四边形。
2. 正交投影:通过平行或垂直于投影面的方法来表示三维物体在二维平面上的投影。
3. 直方图:用矩形表示数据频数或频率分布的图形。
4. 棱柱:具有两个平行且相等的多边形底面,侧面由若干矩形组成的立体图形。