当前位置：文档之家 › 建筑力学第三章 平面力系的平衡方程[精]

建筑力学第三章 平面力系的平衡方程[精]

  • 格式：pptx
  • 大小：827.98 KB
  • 文档页数：24

下载文档原格式

  / 24

合集下载

建筑力学 第三章

建筑力学 第三章


[例] 已知：如图。求梁上分布荷载的合力。 解：荷载分布在一狭长 范围内，如沿构件的轴线分 布，则称为分布荷载。该问 题是一集度按线性变化的
线分布荷载求合力问题。
⒈求合力的大小
而在此微段上的荷载为：
x q 在坐标 x 处取长为 dx 的微段，其集度为： x q l
x dQ qx dx q dx l
x 1 因此，合力Q 的大小为： dQ q dx ql Q l 0 l 2
l
⒉ 求合力作用线的位置
由合力矩定理：M A (Q ) M A (dQ ) 则有：
x Q xc dQ x q dx l 0 l 1 1 2 即： ql xc ql 2 3 2 解得： xc l 3
雨搭 固定端（插入端）约束的构造
车刀
约束反力
①认为Fi这群力在同一
平面内;
② 将Fi向A点简化得一 力和一力偶; ③RA方向不定可用正交 分力YA, XA表示; ④ YA, XA, MA为固定端 约束反力; ⑤ YA, XA限制物体平动,
MA为限制转动。
§3-3-2
平面一般力系的简化结果 合力矩定理
第三章
平面力系的合成与平衡 引 言
力系分为：平面力系、空间力系 ①平面汇交力系 ②平面平行力系(平面力偶系是其中的特殊情况 ) ③平面一般力系(平面任意力系)
平面力系
平面汇交力系： 各力的作用线都在同一平面内且 汇交于一点的力系。
研究方法：图解法，数解法。
例：起重机的挂钩。
§3-1-1 平面汇交力系合成与平衡的图解法 P29
l
2
§3-4
由于
R
平面一般力系的平衡方程
一、平衡的必要与充分条件 =0 作用于简化中心的合力RO=0，则汇交力系平衡； 则力偶矩MO=0 ，因此附加力偶系也平衡。
建筑力学第三章 平面力系的平衡方程

建筑力学第三章 平面力系的平衡方程

刚体等效于只有一个力偶的作用，（因为力偶可以在刚 体平面内任意移动，故这时，主矩与简化中心O无关。）
③ FR≠' 0,MO =0,即简化为一个作用于简化中心的合力。这时， 简化结果就是合力（这个力系的合力）, FR FR'。（此时
与简化中心有关，换个简化中心，主矩不为零）
重庆大学出版社
建筑力学
④ FR' ≠0,MO ≠0,为最任意的情况。此种情况还可以继续
重庆大学出版社
建筑力学
[例] 已知：Q=7.5kN, P=1.2kN , l=2.5m , a=2m , =30o , 求：
BC杆拉力和铰A处的支座反力？
解：（1）选AB梁为研究对象。
C
（2）画受力图
FAy
FBC
A
FAx
l/2 P
B Q
a
Байду номын сангаас
l
A
l/2 P
B Q
a
l
重庆大学出版社
建筑力学
（3）列平衡方程，求未知量。
静不定问题在材料力学,结构力学,弹性力学中 用变形协调条件来求解。
重庆大学出版社
建筑力学
物系平衡问题的特点： ①物体系统平衡，物系中每个单体也是平衡的。 ②每个单体可列3个（平面任意力系）平衡方程，整个系统
可列3n个方程（设物系中有n个物体）。
解物系问题的一般方法：
机构问题： 个体 个体
个体
“各个击破”
力系中各力对于同一点之矩的代数和。
重庆大学出版社
建筑力学
3.2平面力系的平衡方程及应用
FR=0， MO =0，力系平衡
FR =0 为力平衡
MO =0 为力偶也平衡 平面力系平衡的充要条件为：
建筑力学平面一般力系的平衡方程及其应用

建筑力学平面一般力系的平衡方程及其应用


普通高等教育“十一五”国家级规划教材
满足平衡方程时，物体既不能移动，也不能 转动，物体就处于平衡状态。当物体在平面一般 力系的作用下平衡时，可用三个独立的平衡方程 求解三个未知量。 二、平衡方程的其它形式
1.二力矩形式的平衡方程 ∑FX= 0 ∑MA (F ) = 0 ∑MB (F ) = 0 式中x轴不可与A、B两点的连线垂直。
FAx
FNCD = 30kN (↗)
∑MD (F ) = 0
FNCD
- FAy×0.6 + 14 ×0.3 = 0
14kN 8kN
300
300 100
A 30° D B
FAy
C
FAy = 7kN (↑)
∑MC (F ) = 0
- FAx×0.6/ 3- 14 ×0.3
- 8 ×0.6 = 0 FAx = - 25.98kN (←)
5 + FAy= 0
普通高等教育“十一五”国家级规划教材
3kN·m 6kN
3m
6
A
B
5
5
3m
可取∑MB (F ) = 0这一未用过的方程进行校核： 3 + 5×3 - 6×3 = 0
说明计算无误。
普通高等教育“十一五”国家级规划教材
例4-4 梁AB一端是固定端支座，另一端无
约束，这样的梁称为悬臂梁。它承受荷载作用如
普通高等教育“十一五”国家级规划教材
在使用三力矩式计算出结果后，可用另外两 个投影方程之一进行校核。可知计算无误。
例4-6 外伸梁受荷载如图所示。已知均布荷载 集度q=20kN/m,力偶的力偶矩M=38kN·m，集中 力FP=10kN。试求支座A、B的反力。
10kN 20kN/m 38kN·m
建筑力学 平面一般力系的平衡

建筑力学 平面一般力系的平衡


Fcy F 2 sin 60 F ND 20 0.866 8.66 8.66kN
（2） 取梁AC为研究对象,受力图如图(c)
M
A
(F
)
0,
F1
2
F
' Cy
6
F
NB
4
0
F
NB
F1 2
F
' Cy
4
6
10 2
8.66 6 4
17.99kN()
F
x
0,
F
Ax
F
' Cx
0
F
Ax
F
' Cx
10kN()
（1） 取梁CD 为研究对象,受力图如图（b）
M C (F ) 0, F 2 sin 60 2 F ND 4 0
F
ND
sin
60
2
8.66 k N()
F x 0, Fcx F 2 cos60 0
Fcx F 2 cos60 20 0.5 10kN
F y 0, F cy F ND F 2 sin 60 0
F
y
0,
F
Ay
F
NB
F1
F
' Cy
0
F
Ay
F
NB
F1
F
' Cy
17.99
10
8.66
0.67k
N()
求解物体系统平衡问题的要领如下： （1） “拆”：将物体系统从相互联系的地方拆开，在拆开的地方用 相应的约束力代替约束对物体的作用。这样，就把物体系统分解为若 干个单个物体，单个物体受力简单，便于分析。 （2）“ 比”：比较系统的独立平衡方程个数和未知量个数，若彼此 相等，则可根据平衡方程求解出全部未知量。一般来说，由n 个物体 组成的系统，可以建立3n 个独立的平衡方程。 （3） “取”：根据已知条件和所求的未知量，选取研究对象。通常 可先由整体系统的平衡，求出某些待求的未知量，然后再根据需要适 当选取系统中的某些部分为研究对象，求出其余的未知量。 （4） 在各单个物体的受力图上，物体间相互作用的力一定要符合作 用与反作用关系。物体拆开处的作用与反作用关系，是顺次继续求解 未知力的“桥”。在一个物体上，可能某拆开处的相互作用力是未知 的，但求解之后，对与它在该处联系的另一物体就成为已知的了。可 见，作用与反作用关系在这里起“桥”的作用。 （5） 注意选择平衡方程的适当形式和选取适当的坐标轴及矩心，尽 可能做到在一个平衡方程中只含有一个未知量，并尽可能使计算简化。
-平面力系及平衡方程

-平面力系及平衡方程

-平面力系及平衡方程
主矩：指原平面一般力系对简化中心之矩的代数和
mo (Fi ) 。
即 Mo mo (Fi )
MO mO (Fi )
主矩 MO正、负规定 ： 转向 +
–
注意：因主矩等于各力对简化中心之矩的代数和， 所以它的大小和转向一般与简化中心有关。
-平面力系及平衡方程
平面力系简化结果的讨论
如果已知力F在直角坐标轴上的投影Fx和Fy， 则力F的大小和方向可由下式确定
F Fx2 Fy2
tan Fy
Fx
力F的指向和投影Fx和Fy的正负号判定: 如果把力F沿x、y轴分解为两个分力F1、F2， 投影的绝对值等于分力的大小，投影的正负号指明 了分力是沿该轴的正向还是负向。 （力的投影是代数量）。
图1-36平面汇交力系
（2）平面平行力系：力系中各力作用在同一个平面内，且各 个力的作用线都相互平行，如图1-37所示。
图1-37平面平行力系
（3）平面一般力系：力系中各力作用在同一个平面 内，且各个力的作用线在平面内任意分布，如图1-38 所示。
图1-38平面一般力系
二、平面汇交力系 1、力在坐标轴上的投影 设力F作用于物体的A点，如图所示。
(1)FR=0，而MO≠0，原力系合成为力偶。这时力系主矩MO 不随简化中心位置而变。
(2)MO=0，而FR≠0，原力系合成为一个力。作用于点O 的 力FR就是原力系的合力。
(3) FR≠ 0， MO≠0， 原力系简化成一个力偶和一个作用于 点O 的力。这时力系也可合成为一个力。
说明如下：
FR
MO
O
三、平面力偶系
平面力偶系:作用在物体同一平面的许多力偶叫平面力偶系 设有两个力偶
-建筑力学第三章平面力系的合成与平衡

-建筑力学第三章平面力系的合成与平衡


平面汇交力系合成与平衡的几何法小 结
几何法解题步骤：1. 取研究对象；2. 画受力图； 3. 作力多边形；4. 选比例尺； 5. 解出未知数。
几何法解题不足： 1. 精度不够，误差大； 2. 作图要求精度高； 3. 不能表达各个量之间的函数关系。
平面汇交力系合成与平衡的另一种方法： 解析法(重点掌 握)。
R0
Rx2

R
2 y
0
或：力系中所有力在各个坐标轴上投影的代
数和分别等于零。
Rx Fx 0 Ry Fy 0
为平衡的充要条件， 也叫平衡方程
解析法求解汇交力系平衡问题的一般步骤:
1.选-对像;即依需选分离体，分离体选取应最好含题设
的已知条件; 2.画-分离体受力图,作到准确无误;
应用力线平移定理，可将刚体上平面任意力系中各个力
的作用线全部平行移到作用面内某一给定点O 。从而这
力系被分解为平面汇交力系和平面力偶系。这种变换的
方法称为力系向给定点O 的简化。点O 称为简化中心。 R0 -----主矢,与简化中心选取无关; M0 ---主矩,与简化中心有关。
2、主矢和主矩 (1)主矢R0
F3 F2
D
C
F2 F4 F3
R
F4
R
F4
E
E
3、汇交力系的合成结果
汇交力系可以合成为一个力，合力作用在力系
的公共作用点，它等于这些力的矢量和，并可由这
力系的力多边形的封闭边表示。
矢量的表达式：R F1 F 2
F1
A F2
F4 F3
F1
A
B F2
R
C
F3
D
F4
n
第3讲平面力系的平衡

第3讲平面力系的平衡


M=MB(FP)=-FP×e=-100kN×0.4m=-40kN·m
负号表示该附加力偶的转向是顺时针转向的。
2.平面一般力系向作用平面内任一点的简化 平面一般力系向作用平面内任一点的简化
F'Rx = ∑Fx F'Ry = ∑Fy
y MO F'R α x
O·
FR' = Fx ' 2 + Fy ' 2
B
30° 60°
A
C W
[例1] 支架由直杆AB、AC构成，A、B、C三处都是铰链，在A点 例 悬挂重量为W=20kN的重物，如图所示，求杆AB、AC所受的力。杆 的自重不计。
B y FAB
30°
[解]（1）选取研究对象 解 （2）画受力图 （3）建立坐标系 3 （4）列平衡方程并解之 ∑Fx＝0， －FAC－Wcos60°＝0 FAC ＝－Wcos60°＝－10kN （压） ∑Fy＝0， FAB－Wsin60°＝0 FAB ＝Wsin60°＝17.3 kN （拉）
第3讲 平面力系平衡
主讲教师：王艳 联系方式：wy_01021604@
预备知识
平面一般力系的合成
1.力的平移定理 力的平移定理
如果一个力大小、方向均不变，只是将力的作用线平行移 动到某一点，称为力向一点平移
F′ A· O F （a） A· O （b） A·
F′ M O （c）
1.力的平移定理 力的平移定理
F F′
O。 A。 O。 d
F
A。
F′
M A。 O。
F"
M=Fd=MO(F)
1.力的平移定理 力的平移定理
F F′
O。 A。 O。 d
F
平面力系的平衡方程及应用

平面力系的平衡方程及应用

研究方法：几何法，解析法。
各力的作用线都在同一平面内且 汇交于一点的力系。
正文
力在直角坐标轴上的投影
1
Fx=F·cosa ; Fy=F·sina = F ·cosb
说明： （1）力在坐标轴上的投影为代数量； （2）力的指向与坐标轴的正向一致时，力的投影为正值，否则为负。
正文
合力投影定理
推论1：力偶对刚体的作用与力偶在其作用面内的位置无关；
推论2：只要保持力偶矩的大小和力偶的转向不变，可以同时改变力偶中力的大小和力偶臂的长短，而不改变力偶对刚体的作用。
M
M
M
力偶表示方法
正文
思考：
力偶与力的异同
共同点：单位统一，符号规定统一。 差异点：1.力矩随矩心位置不同而变化；力 偶矩对物体作用效果与矩心选取无关。 2.力偶矩可以完全描述一个力偶；力对点之矩不能完全描述一个力。
′
F
M
单 手 攻 丝
正文
平面任意力系的简化
1
平面一般力系向平面内一点简化
F3
F1
F2
O
O
O
F
R′
MO
F
1′
M1
F1 =F1
′ M1=MO(F1)
F
2′
M2
F
3′
M3
F2 =F2
′ M2=MO(F2)
F3 =F3
′ M3=MO(F3)
简化中心
O
FR=F1+F2+F3= F1+F2+F3 MO=M1+M2+M3=MO(F1)+ MO(F2) + MO(F3)
正文
平面力偶系的合成与平衡
平面力系的平衡方程

平面力系的平衡方程


Ry = 0 : − P − P − P + FA + FB = 0 3 1 2
7 P + P − 2P 3 FB = 2 1 2
P − 5P + 4 P
−NB ⋅ a − P ⋅ b − Q ⋅ c = 0
N B = −( Pb + Qc ) / a
Rx = 0 → N Ax = − N b
Ry = 0 → N Ay = P + Q
例6 第5章 章
力 系 简 化 与 平 衡 问 题
塔式起重机的机架重P1，作用线通过塔架的 中心。最大起重量P2 ，最大悬臂长为12m， 轨道AB的间距为4m。平衡重P3 到机身中心 线距离为6m。 1.保证起重机在满载 和空载时都不致翻 到，平衡重P3 应为 多少？ 2.当配重为P3 时求满 载时轨道A、B的约 束力。
θ
NA
C
θ
NB
B
ϕ
A
P
θ
例2 第5章 章
力 系 简 化 与 平 衡 问 题
AB是吊车梁，BC是钢索，A端支承可简化为 铰链支座。设已知电葫芦和提升重物共重P= 5kN, θ = 25º，a=2m，l = 2.5m。吊车梁的自 重略去不计，求钢索BC和铰A的约束力。
C
θ
A D B
P
例2 第5章 章
mB = − N A a sin α + P[(l − a sin α ) sin α + a ] − P(l − a cos α ) cos α = 0
Rx = N B sin α − N A cos α = 0
能否用Ry = 0 ?
从这三个方程可以解出NA，NB和α 。
例4 第5章 章
平衡方程及应用

平衡方程及应用


FAx 31kN
FB
FAy G1 G2 0
FAy 50kN
FAx FAy
G1 G2
平面一般力系的平衡方程及应用
例2-20 已知：F＝8kN，M＝4kN·m求A、B处的约束力。
M
解：取刚架AB为研究对象，受力如图所示。
Fx 0 F FAx 0
F
FAx F 8kN
【例 2-7】
平面力系的平衡方程及应用
4.平面力偶系的平衡方程 作用在物体同一平面内力的许多力偶，称为平面 力偶系。
平面力偶系平
衡的必要充分 条件是：力偶 系中各力偶矩 的代数和为零。
M=M1+M2+…+Mn=0
【例2-8】
平面力系的平衡方程及应用
通过以上各例可归纳出求解物体系统平衡问题的一般步骤: （1）分析题意,选取适当的研究对象
平面力系的平衡方程及应用
1.平面一般力系的平衡方程
若使刚体处于平衡，则必须满足作用于 刚体上的合力矢FR=0，合力偶矩M=0，即
FR ( Fx )2 ( Fy )2 , MO MO(Fi )

Fx Fy
0 0

M o 0
—— 平面一般力系的平衡方 程（基本形式、两影一矩式）
平衡 方程
平面力系的平衡方程及应用
1.平面一般力系实例
平面力系的平衡方程及应用
1.平面一般力系实例
y
B
M
FAy
A
FAx
C F
x
FNC
F
a b
h
G
FA
H
FB FNB
FNA
平面力系的平衡方程及应用
力系的平衡ppt课件

力系的平衡ppt课件


A
x
A、B 连线不垂直于x 轴
（两矩式）
MA（F）= 0 MB（F）= 0 MC（F）= 0 （三矩式）
C B
A
C
A、B、C三点不
在同一条直线上 17
平面任意力系平衡方程讨论：
Fx = 0 Fy = 0 MO= 0
平面任意力系：三个独立的平衡方程，可解3个未知量 平面汇交力系：二个独立的平衡方程，可解2个未知量 平面平行力系：二个独立的平衡方程，可解2个未知量
y
F’Cy
F
F’Cx C
E
G
O FBx
B x
FBy
Fx 0,
FCx FBx 0
Fy 0,
FCy FBy F G 0
MC F 0,
FAx 32.89 kN, FAy 2.32 kN, M A 10.37 kN 3m9
例9 图示三铰拱桥，由左右两段借铰链C连
接，又用铰链A，B与基础相连接。已知每 段重G = 40 kN，重心分别在D，E处，且桥 面受一集中载荷F =10 kN。设各铰链都是光 滑的，试求平衡时各铰链约束力。
注意：对任意一点的主矩为零。
平衡方程：
Fx 0
Mx(F )0
Fy 0
My(F )0
Fz 0
Mz( F ) 0
3
一、平面汇交力系
力系的平衡条件：主矢为零
平面汇交力系平衡方程：
Fx 0
平衡几何条件：
Fy 0
汇交力系的力多边形自行封闭
求解方法： 1、 几何法：利用力多边形自行封闭求解 2、 解析法：利用平衡方程求解
第三章 力系的平衡
本章重点：
1、力系平衡方程及其应用 2、物体系统平衡问题分析 3、桁架内力分析

工程力学教学课件之三平面任意力系平衡方程


0
0
Fx 0
或
M
0
(
F
)
0
◆ 课题3–2 固定端约束 均布载荷求力矩
一、平衡方程的其它形式
例3-5 图示支架由杆AB、BC组成，A、C、D处均为光滑铰链，在
AB上作用F力，集中力偶M=Fa，=30°，试求杆件AB的约束力。
解：1.取AB杆为研究对象画受力图
FM A
B
2.平衡方程求约束力
M A (F ) 0 : FB sin 30 2a F a M 0 FB 2F Fx 0 : FAx FBcos30 0 FAx FBcos30 3F Fy 0 : FAy FB sin 30 F 0 FAy 0
2.平面力偶系
MO(F) 0
平面力偶系有一个独立的平衡 方程，解出一个未知数。
3.平面平行力系
Fy 0 M0(F)
0
平面平行力系有一组二个独立 的平衡方程，解出二个未知数。
4.平面任意力系
Fx 0 Fy 0
平面任意力系有一组三个独立 的平衡方程，解出三个未知数。
M 0 (F ) 0
y
C
F M0 F
A F
B x
FR ( Fx )2 ( Fy )2 0
2.选A点为简化中心，求力系的主矩
M0 MA(F) F sin 60 AB F AB 3 / 2
简化结果是一平面力偶系(取其它点为简化中心，结果不变，
因为本来就已构成平面力偶系)。
二、平面任意力系的平衡方程
1.平衡条件 平面任意力系平衡的必充条件为FR=0 Ｍ0=0。即
2.均布载荷求力矩： 均布载荷对平面上任意点O的力矩等于 其合力FQ与分布长度中点到矩心距离的乘积，即

建筑力学3-平面力系


图3.4


若已知力F的大小及其与x轴所夹的锐角α，则力F在坐标轴 上的投影Fx和Fy可按下式计算 Fx=±Fcosα Fy=±Fsinα 力在坐标轴上的投影有两种特殊情况： (1) 当力与坐标轴垂直时，力在该轴上的投影等于零。 (2) 当力与坐标轴平行时，力在该轴上的投影的绝对值等于 力的大小。
图3.11
3.3.2 平面一般力系的合成


平面一般力系向作用面内任一点O简化后，一般可 以得到一个力和一个力偶，但实际上根据主矢和主矩是 否存在，可能出现下列四种情况： (1) R′=0, MO≠0; (2) R′≠0, MO=0; (3) R′≠0, MO≠0; (4) R′=0，MO=0。

总结：
一，概念： 1，平面一般力系 2，平面力系的合成： ——主矢量Ro与主力偶矩Mo 3，关于主矢量Ro与主力偶矩Mo特例的讨论： 1）Ro≠0, Mo=0；原力系向o点简化后得一个力Ro， Ro即 为原力系的合力； 2) Ro=0, Mo ≠ 0；原力系向o点简化后得一个力偶Mo， Mo 即为原力系的合力偶矩Mo； 3) Ro=0, Mo=0；原力系为一平衡力系。




对平面汇交力系F1′、F2′、…、Fn′可以合成为作用 在O点的一个力R′（图3.11(c))，这个力R′称为原平面一 般力系的主矢。 对所得的附加力偶系可以合成为一个力偶（图3.11 （c)），这个力偶的力偶矩MO称为原平面一般力系对 简化中心O点的主矩。由平面力偶系合成的理论可知， 主矩MO为 MO=m1+m2+…+mn 而 m1=mO(F1),m2=mO(F2),…,mn=mO(Fn)

பைடு நூலகம்

理论力学课件 平面力系平衡方程及应用

G3(6 − 2 )− G1 × 2 − G2 (12 + 2 )+ FB × 4 = 0
∑ Fy = 0
− G3 − G1 − G2 + FA + FB = 0 FB = 870 kN FA = 210 kN
3.2 平面力系平衡方程及应用
平面任意力系 ∑ Fx = 0 ∑ Fy = 0 ∑ MO = 0
∑ M A = 0 G3 (6 − 2 ) − G1 × 2 = 0
G 3 = 350 kN 则有 75 kN＜G3＜350 kN
3.2 平面力系平衡方程及应用
G3
6m
G1 12 m
A
B
FA2 m 2 mFB
2. 取G3=180 kN，求满载时轨道 A ， B给起重机轮子的约束力。
G2
∑MA =0
∑ ∑ 平面平行力系
Fy = 0
MO = 0
∑ ∑ 平面力系 平面汇交力系
Fx = 0
Fy = 0
平面力偶系
∑M =0
证明：
F1
F
A1
F2
A A2
A
=
A3
A3
F3
F3
3.2 平面力系平衡方程及应用
三力平衡汇交定理用来确定未知力方向使用，但这样做通 常不方便。
3.2 平面力系平衡方程及应用
思考
三铰拱受力是否正确？ 错误
3.2 平面力系平衡方程及应用
平面汇交力系平衡几何法
物体受汇交力系作用，力系若平衡，则力多边形封 闭。
FC
FA
练习：
FB
2、研究对象： 整体
− FAl + m = 0
FA
=
FB

理论力学第3章力系平衡方程及应用


a
分布力(均布载荷) 合力作用线位于AB
中点。
3.1 平面力系平衡方程
a
【解】
y M=qa2 a
2qa
F3
C
FAx
A
aFAy
45
B
D
x
2a FB a
F3 2qa
MA 0
q 2 2 a q a a F B 2 a 2 q sa 4 i 3 n a 5 0
FB 2qa
Fx 0 FAx2qcao4s50 FAx qa
C
【解】 F2
构件CGB（ 图b）
F2
构件AED
（图c）
C
R
D
45
FC
FD
D
G
45
F1
E
a
F1
E
a
A
B
G 图b
FBy
图c A FAx
MA
FAy
构件CD（图a ）
3个未知量 B FBx
4个未知量
F'C
3个独立方程
3个独立方程
【基本思路】
C R
杆CGB受力图计算FCAED受力图
计算A处的反力(偶)；CGB受力图计算
3.2 平面物体系平衡问题
q
C
B
30
FC FBy
l
l
【解】 杆CB
FBx
MB 0
FCco3s0l qll/2 0
FC
3 ql 30.5kN/m 2m 0.577kN
3
3
3.2 平面物体系平衡问题
【解】整体
FAy
l
l
l
Fx 0
MA
A
FAx

平面一般力系的平衡方程共有三组九个方程

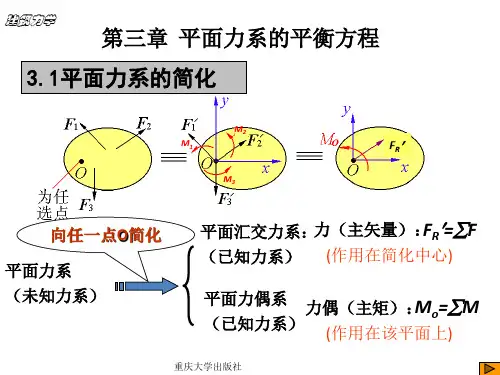
平面一般力系的平衡方程共有三组九个方程平面一般力系的平衡方程是力学中的基本概念之一，用来描述物体在平面上处于力学平衡的条件。

这些方程由牛顿第二定律和力的合成原理推导得到，主要包括平衡条件和力的平衡条件。

首先，平面一般力系的平衡条件是指物体在平面上的合力和合力矩都为零，即物体不发生任何平动和转动的情况下，处于力学平衡状态。

合力为零表示物体受到的所有力在平面内互相抵消；合力矩为零表示物体受到的力矩合力为零，即物体不会发生转动。

其次，力的平衡条件是指物体受到的所有力在平面内满足力的平衡方程，可以分为三组方程：水平方向的平衡方程、竖直方向的平衡方程和力矩平衡方程。

水平方向的平衡方程描述了物体在水平方向上受到的力的平衡条件。

对于一个平面一般力系，物体在水平方向上受到的合力为零，可以表示为∑Fx = 0。

其中，∑Fx表示所有作用在物体上的力在水平方向上的分量的代数和。

竖直方向的平衡方程描述了物体在竖直方向上受到的力的平衡条件。

对于一个平面一般力系，物体在竖直方向上受到的合力为零，可以表示为∑Fy = 0。

其中，∑Fy表示所有作用在物体上的力在竖直方向上的分量的代数和。

力矩平衡方程描述了物体受到的所有力矩合力为零的平衡条件。

对于一个平面一般力系，物体受到的合力矩为零，可以表示为∑M = 0。

其中，∑M表示所有作用在物体上的力对物体某一点产生的力矩的代数和。

平面一般力系的平衡方程共有三组九个方程，即水平方向的平衡方程、竖直方向的平衡方程和力矩平衡方程。

这些方程可以精确地描述物体处于力学平衡的条件，并可以用于求解各个力的大小和方向。

在实际应用中，平面一般力系的平衡方程被广泛应用于工程领域，如结构力学、力学设计和力学分析等。

通过求解平衡方程，可以确定结构物体的静力特性，设计稳定性良好的工程结构，并可以预测结构物体在受力过程中的应力和变形情况。

总之，平面一般力系的平衡方程是力学中的基本概念之一，提供了描述物体在平面上力学平衡的数学工具。

3平面力系的平衡方程

第三章 力系的平衡条件与平衡方程
§3-1 平面任意力系的平衡条件 和平衡方程
平面任意力系平衡的充要条件是：FR 0 M o 0
因为
F R
(
F x
)2
(
F y
)2
M O
M
O
(
F i
)
所以有：
Fx Fy
0 0
M o 0
平面任意力系平衡方程的三种形式
一般式 二矩式
F x
0
F y
0
M A 0
2 fs
已知：物块重P, 鼓轮重心位于 O1 处，闸杆重量不计， fs , 各尺寸如图所示：
求： 制动鼓轮所需铅直力F。
O1
解：分别取闸杆与鼓轮为研究对象 设鼓轮被制动处于平衡状态
对鼓轮， M O1 0 rFT RFs 0
对闸杆，MO 0 且 Fs fs FN
Fa FN b Fsc 0
FR l2 R2
取轮,画受力图：
Fix 0
Fox FA sin 0
Fox
FR l2 R2
Fiy 0 Foy FA cos 0 Foy F
Mo 0 FA cos R M 0 M FR
§3-3 物体系的平衡·静定和超静定问题
已知: F=20kN, q=10kN/m, M 20kNm, L=1m; 求: A,B处的约束力.
Fy 0 FA FB FN 0
M A 0
F
(a
b 2
)
FB
d
FBN
b
0
FA fs FAN
FB fs FBN
解得： a b
2 fs
则：挺杆不被卡住时，a
b 2 fs
。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
建筑力学
第三章 平面力系的平衡方程
3.1平面力系的简化
M2
M1
FR
M3
向任一点O简化
平面力系 （未知力系）
平面汇交力系：力（主矢量）：FR=F
（已知力系） (作用在简化中心)
平（面已力知偶力系系）力偶(作（用主在矩该）平：面M上o=)M
重庆大学出版社
建筑力学
一般情况：
主矢 : FR ' F1 F2 F3 Fi
FAy
FBC
A

FAx
l/2 a
P
B Q
l
MB (Fi ) 0 MC (Fi ) 0
l FAyl P 2 Q(l a) 0
FAx l

tg

P
l 2

Qa

0
FAy 2.1kN
FAx 11.4kN
重庆大学出版社
建筑力学
[例] 已知：P=20kN, M=16kN·m, q=20kN/m, a=0.8m
20 20 0.8 12
12(kN)
24(kN)
重庆大学出版社
建筑力学
FAy FAx
FB
静定（未知数三个）
FAy FAx
FBy FBx
静不定（未知数四个）
独立方程数目≥未知数数目时，是静定问题（可求解） 独立方程数目<未知数数目时，是静不定问题（超静定问题）
静不定问题在材料力学,结构力学,弹性力学中 用变形协调条件来求解。
简化中心 (与简化中心位置无关) [因主矢等于各力的矢量和]
重庆大学出版社
建筑力学
主矩MO （转动效应）
大小：MO MO (Fi )
方向： 方向规定 + —
简化中心： (与简化中心有关) （因主矩等于各力对简化中心取矩的代数和）
重庆大学出版社
建筑力学
简化结果分析 合力矩定理
简化结果： 主矢FR'，主矩 MO ，下面分别讨论。 ① FR' =0， MO =0，则力系平衡,下节专门讨论。 ② FR' =0, MO≠0，即简化结果为一合力偶, M=MO 此时
重庆大学出版社
建筑力学
[例] 已知：q， a , P=qa, M=Pa，求：A、B两点的支座反力？
解：① 选AB梁为研究对象。
② 画受力图
qP
FAy
qP
FB
A
B
M
2a
a
FAx
A
M
B
列平衡方程，求未知量。
Fx 0
Fy 0
FAx 0
FB FAy P 2qa 0,
M A(Fi ) 0
FAx
FBC
sin

l

P

l 2

Qa

0
FAy
FBC
A

l/2 P
B Q
a
l
FBC (Pl / 2 Qa) /(l sin ) 13.2kN
Fx 0
Fy 0
FAx FBC cos 0
FAx FBC cos 11.4kN
求：A、B的支反力。
q FA M FB
解：研究AB梁
P
MA(F ) 0;
A
B
a
a
a
FB

a

q

a

a 2

M

P

2a

0
Fy 0
FA FB qa P 0
FB

qa 2

M a
2P
20 0.8 16 2 20
2
0.8
FA P qa FB
a
l
MB (Fi ) 0
l FAyl P 2 Q(l a) 0
FAy 2.1kN
Fx 0
FAx FBC cos 0
FAx 11.4kN
重庆大学出版社
建筑力学
M A(Fi ) 0
FBC
sin

l

P

l 2

Qa

0
FBC 13.2KN
重庆大学出版社
建筑力学
[例] 已知：Q=7.5kN, P=1.2kN , l=2.5m , a=2m , =30o , 求：
BC杆拉力和铰A处的支座反力？
解：（1）选AB梁为研究对象。
C
（2）画受力图
FAy
FBC
A

FAx
l/2 P
B Q
a
l
A

l/2 P
B Q
a
l
重庆大学出版社
建筑力学
（3）列平衡方程，求未知量。
4qa FAy 3
M A (Fi ) 0 P 2a q 2a a M FB 3a 0
5qa FB 3
重庆大学出版社
建筑力学
平面力系的平衡方程:
① 基本式（一矩式） ②二矩式
③三矩式
Fx 0
Fy 0
Fx 0 M A(Fi ) 0
主矩： MO M1 M2 M3
MO (F1) MO (F2) MO (Fi )
大小：FR ' F 'Rx2 F 'Ry2 ( Fx )2 ( Fy )2
主矢 FR'
（移动效应）
方向： tan1 FRy
FRx
tan1
Fy Fx
M A(Fi ) 0 MB (Fi ) 0
MO (Fi ) 0
MB (Fi ) 0
MC (Fi ) 0
条件：x 轴不垂直 于AB连线
条件：A,B,C不在 同一直线上
只有三个独立方程，只能求出三个未知数。
投影轴和矩心是任意选取的，一般先取矩。矩心选 择在多个未知力的交点上；投影轴尽量与未知力垂 直或平行。
重庆大学出版社
建筑力学
物系平衡问题的特点： ①物体系统平衡，物系中每个单体也是平衡的。 ②每个单体可列3个（平面任意力系）平衡方程，整个系统
④ FR' ≠0,MO ≠0,为最任意的情况。此种情况还可以继续
简化为一个合力 FR。
FR FR FR
FR'
M0 FR d
FR'FR源自FRFR合力的大小等于原力系的主矢 FR FR' F
合力的作用线位置
d MO FR
结论：平面力系的简化结果 ：①合力偶MO ； ②合力 FR
刚体等效于只有一个力偶的作用，（因为力偶可以在刚 体平面内任意移动，故这时，主矩与简化中心O无关。）
③ FR≠' 0,MO =0,即简化为一个作用于简化中心的合力。这时， 简化结果就是合力（这个力系的合力）, FR FR'。（此时
与简化中心有关，换个简化中心，主矩不为零）
重庆大学出版社
建筑力学
FAy FBC sin P Q 0 FAy P Q FBC sin 2.1kN
重庆大学出版社
建筑力学
（3）列平衡方程，求未知量。
M A(Fi ) 0
FAx
FBC
sin

l

P

l 2

Qa

0
FBC 13.2KN
FAy
FBC
A

l/2 P
B Q