当前位置：文档之家 › 时间序列分析 第五章-非平稳序列的随机分析

时间序列分析 第五章-非平稳序列的随机分析

  • 格式：doc
  • 大小：3.18 MB
  • 文档页数：23

下载文档原格式

  / 23

合集下载

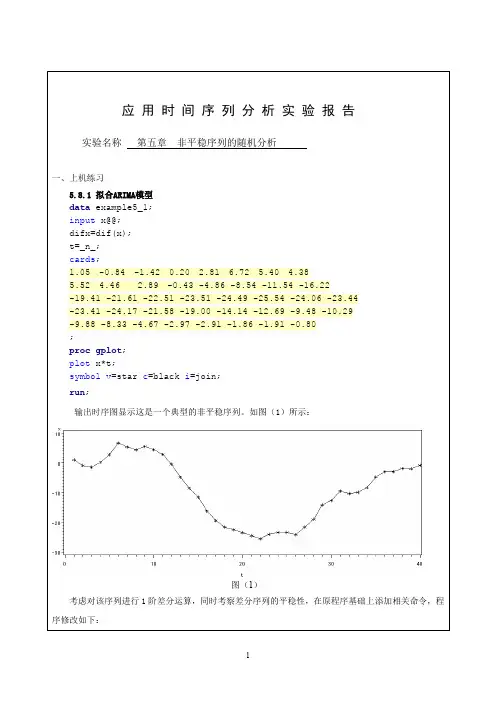
时间序列分析第五章非平稳序列的随机分析

时间序列分析第五章非平稳序列的随机分析
xt xt xt1
考察差分运算对该序列线性趋势信息的提 取作用
2020/3/12
时间序列分析
差分前后时序图
原序列时序图
差分后序列时序图
2020/3/12
时间序列分析
例5.2
尝试提取1950年——1999年北京市民用 车辆拥有量序列的确定性信息
2020/3/12
时间序列分析
Green函数递推公式
1 1 1 2 1 1 2 2

j 1 j1 pd j pd j
t


2
,
E(
t
s
)

0,
s

t
Exs t 0,s t
2020/3/12
时间序列分析
ARIMA 模型族
d=0 ARIMA(p,d,q)=ARMA(p,q)
P=0 ARIMA(P,d,q)=IMA(d,q)
q=0 ARIMA(P,d,q)=ARI(p,d)
d=1,P=q=0 ARIMA(P,d,q)=random walk model
差分后序列时序图
一阶差分
二阶差分
2020/3/12
时间序列分析
例5.3
差分运算提取1962年1月——1975年12月平均 每头奶牛的月产奶量序列中的确定性信息
2020/3/12
时间序列分析
差分后差分
2020/3/12
时间序列分析
过差分
足够多次的差分运算可以充分地提取原 序列中的非平稳确定性信息
2020/3/12
时间序列分析
随机游走模型( random walk)
模型结构

8_第五章_非平稳时间序列的随机分析(I)_ARIMA

8_第五章_非平稳时间序列的随机分析(I)_ARIMA

0 1960
1970
1980
1990
差分后的序列，可以看出已经消除了线性趋势，呈现平稳的随机波动
dif 60
50
40
30
20
10
0
-10
-20
-30
-40 1960
1970
1980
1990
2000
注意，差分后的序列样本少了一个(为什么？)
思考：为什么 1 阶差分可以消除线性趋势？
(2) 序列含有曲线趋势，通常低阶（2 阶或者 3 阶）的差分就可以消除趋势项 【例 5.2】1950-1999 年北京市民用车辆拥有量序列 原始时间序列，有曲线趋势
15
0.21892 |
16
0.00855 |
17
0.05496 |
18
0.01825 |
.
|***********
|
. **|
.
|
.
|*
.
|
. *****|
.
|
.
|*** .
|
. ****|
.
|
.
|*
.
|
.
|**** .
|
.
|*
.
|
. *****|
.
|
.
|*
.
|
.
|*
.
|
. *|
.
|
. ***|
.
|
5.1.2 差分方式的选择
(1) 序列蕴含着线性趋势，则 1 阶差分就可以实现趋势平稳 【例 5.1】1964 年-1999 年中国纱年产量 data a; input year sha; dif=dif(sha); cards; 数据; proc gplot; plot sha*year dif*year; symbol v=star c=red i=join; run; 原始时间序列，可以看出是非平稳的，有近似线性趋势

时间序列分析 第五章-非平稳序列的随机分析

时间序列分析 第五章-非平稳序列的随机分析

图（1）考虑对该序列进行1阶差分运算，同时考察差分序列的平稳性，在原程序基础上添加相关命令，程序修改如下：图（2）时序图显示差分后序列difx没有明显的非平稳特征。

（2）“identify var=x(1);”，使用该命令可以识别差分后序列的平稳性。

纯随机性和适当的拟合图（6）普通最小二乘估计结果图（8）最终拟合模型输出结果图（9）拟合效果图图（12）带有延迟因变量的回归模型拟合效果图5.8.3拟合GARCH模型SAS系统中AUTOREG过程功能非常强大，不仅可以提供上述的分析功能，还可以提供异方差性检验乃至条件异方差模型建模。

以临时数据集example5_3数据为例，介绍GARCH模型的拟合，相关命令如下：data example5_3;input x@@;t=_n_;cards;10.77 13.30 16.64 19.54 18.97 20.52 24.3623.51 27.16 30.80 31.84 31.63 32.68 34.9033.85 33.09 35.46 35.32 39.94 37.47 35.2433.03 32.67 35.20 32.36 32.34 38.45 38.1732.14 39.70 49.42 47.86 48.34 62.50 63.5667.61 64.59 66.17 67.50 76.12 79.31 78.8581.34 87.06 86.41 93.20 82.95 72.96 61.1061.27 71.58 88.34 98.70 97.31 97.17 91.1780.20 85.12 81.40 70.87 57.75 52.35 67.5087.95 85.46 84.55 98.16 102.42 113.02 119.95122.37 126.96 122.79 127.96 139.20 141.05 140.87137.08 145.53 145.59 134.36 122.54 106.92 97.23110.39 132.40 152.30 154.91 152.69 162.67 160.31142.57 146.54 153.83 141.81 157.83 161.79 142.07139.43 140.92 154.61 172.33 191.78 199.27 197.57189.29 181.49 166.84 154.28 150.12 165.17 170.32;proc gplot data=example5_3;plot x*t=1;symbol1c=black i=join v=start;proc autoreg data=example5_3;model x=t/nlag=5dwprob archtest;model x=t/nlag=2noint garch=(p=1,q=1);output out=out p=p residual=residual lcl=lcl ucl=ucl cev=cev;data out;set out;l95=-1.96*sqrt(51.42515);u95=1.96*sqrt(51.42515);Lcl_GARCH=-1.96*sqrt(cev);Ucl_GARCH=1.96*sqrt(cev);Lcl_p=p-1.96*sqrt(cev);Ucl_p=p+1.96*sqrt(cev);proc gplot data=out;plot residual*t=2 l95*t=3 Lcl_GARCH*t=4 u95*t=3 Ucl_GARCH*t=4/overlay; plot x*t=5 lcl*t=3 LCL_p*t=4 ucl*t=3 UCL_p*t=4/overlay;symbol2c=green i=needle v=none;symbol3v=black i=join c=none w=2l=2;symbol4c=red i=join v=none;symbol5c=green i=join v=none;run;该序列输出时序图如图（13）所示。

时 间 序 列 分 析 实 验 报 告实例

时 间 序 列 分 析 实 验 报 告实例

应用时间序列分析实验报告实验名称第五章非平稳序列的随机分析专业班级姓名学号一、上机练习程序及其结果分析：data ex3_1;input x@@;time=_n_;cards;0.30 -0.45 0.36 0.00 0.17 0.45 2.154.42 3.48 2.99 1.74 2.40 0.11 0.960.21 -0.10 -1.27 -1.45 -1.19 -1.47 -1.34-1.02 -0.27 0.14 -0.07 0.10 -0.15 -0.36-0.50 -1.93 -1.49 -2.35 -2.18 -0.39 -0.52-2.24 -3.46 -3.97 -4.60 -3.09 -2.19 -1.210.78 0.88 2.07 1.44 1.50 0.29 -0.36-0.97 -0.30 -0.28 0.80 0.91 1.95 1.771.80 0.56 -0.11 0.10 -0.56 -1.34 -2.470.07 -0.69 -1.96 0.04 1.59 0.20 0.391.06 -0.39 -0.162.07 1.35 1.46 1.500.94 -0.08 -0.66 -0.21 -0.77 -0.52 0.05;procgplot data=ex3_1;plot x*time=1;symbol1c=red I=join v=star;run;结果分析：上图是数据对应的时序图，从图上曲线分析来看，数据并没有周期性或者趋向性规律，因而可以初步判断这是平稳数列。

procarima data=ex3_1;identifyVar=x nlag=8;run;结果分析：本过程中，我们建立了8阶自回归分析模型，图上依次是变量的描述性统计量、样本自相关图、样本逆相关图和样本偏自相关图。

由于本次实验探究的是平稳序列，因而样本逆相关图先不作分析。

从自相关图来看，自相关系数趋于0的速度是比较快的，再结合时序图来看，可以确定这组数列是属于平稳数列。

【2019年整理】时间序列分析--第五章非平稳序列的随机分析

【2019年整理】时间序列分析--第五章非平稳序列的随机分析

尝试提取1950年——1999年北京市民用 车辆拥有量序列的确定性信息
4/8/2019
时间序列分析
差分后序列时序图

一阶差分

二阶差分
4/8/2019
时间序列分析
例5.3

差分运算提取1962年1月——1975年12月平均 每头奶牛的月产奶量序列中的确定性信息
4/8/2019
时间序列分析
差分后序列时序图
4/8/2019
时间序列分析
差分方式的选择



序列蕴含着显著的线性趋势，一阶差分 就可以实现趋势平稳 序列蕴含着曲线趋势，通常低阶（二阶 或三阶）差分就可以提取出曲线趋势的 影响 对于蕴含着固定周期的序列进行步长为 周期长度的差分运算，通常可以较好地 提取周期信息
时间序列分析
4/8/2019
例5.1
时间序列分析
ARIMA模型建模步骤
获 得 观 察 值 序 列 平稳性 检验 N 差分 运算 Y 白噪声 检验 N 拟合 ARMA 模型
时间序列分析
Y
分 析 结 束
4/8/2019
例5.6

对1952年——1988年中国农业实际国民 收入指数序列建模
4/8/2019
时间序列分析
一阶差分序列时序图
第五章
非平稳序列的随机分析
4/8/2019
时间序列分析
本章结构


差分运算 ARIMA模型 Auto-Regressive模型 异方差的性质 方差齐性变化 条件异方差模型
4/8/2019
时间序列分析
5.1 差分运算

差分运算的实质 差分方式的选择 过差分

时间序列分析--第五章非平稳序列的随机分析

时间序列分析--第五章非平稳序列的随机分析

50
乘积季节模型
使用场合
序列的季节效应、长期趋势效应和随机波动之间有着复 杂地相互关联性，简单的季节模型不能充分地提取其中 的相关关系
构造原理
短期相关性用低阶ARMA(p,q)模型提取
季节相关性用以周期步长S为单位的ARMA(P,Q)模型提取
假设短期相关和季节效应之间具有乘积关系，模型结构
3
差分运算的实质
差分方法是一种非常简便、有效的确定 性信息提取方法
Cramer分解定理在理论上保证了适当阶 数的差分一定可以充分提取确定性信息
差分运算的实质是使用自回归的方式提 取确定性信息
d
d xt (1 B)d xt (1)i Cdi xti i0
5/10/2019
模型中有部分系数省缺了，那么该模型 称为疏系数模型。
5/10/2019
课件
34
疏系数模型类型
如果只是自相关部分有省缺系数，那么该疏系 数模型可以简记为ARIMA(( p1,, pm ), d, q)
p1,, pm 为非零自相关系数的阶数
如果只是移动平滑部分有省缺系数，那么该疏 系数模型可以简记为 ARIMA( p, d, (q1,, qn ))
26
建模
定阶
ARIMA(0,1,1)
参数估计
(1 B)xt 4.99661 (1 0.70766 B) t
Var(t ) 56.48763
模型检验
模型显著 参数显著
5/10/2019
课件
27
ARIMA模型预测
原则
最小均方误差预测原理
Green函数递推公式
一阶差分

6-非平稳序列的随机分析


• • • • •
# R code for simulating a random walk with, say 60, iid standard normal errors n=60 set.seed(12345) # intialize the random number so that the simulation can be reproducible. sim.random.walk=ts(cumsum(rnorm(n)),freq=1,start=1) plot(sim.random.walk,type='o',ylab='Another Random Walk')
模型检验
残差白噪声检验 延迟 阶数 6 12 18
2统 计量
参数显著性检验 待估 参数
2统 计量
P值
0.2120 0.4002
P值
4.50 9.42
1
12 1
-4.66 <0.0001 23.03 <0.0001 -6.81 <0.0001
20.58 0.1507
结果
模型显著
参数均显著
• 给定季节指数
St St
• 建立季节自回归模型
Tt 0 1 xt m l xt lm
• etc
3.考虑残差
• • • • AR MA ARMA etc
5.4 异方差的性质
• 异方差的定义
– 如果随机误差序列的方差会随着时间的变化而 变化，这种情况被称作为异方差
疏系数模型
• ARIMA(p,d,q)模型是指d阶差分后自相关最 高阶数为p，移动平均最高阶数为q的模型， 通常它包含p+q个独立的未知系数： 1 ,, p ,1 ,, q

非平稳时间序列解析

2 预测方差为{1+(1 12 ) (1 12 s-1 )} 2
动态乘子的比较
趋势平稳过程 动态乘子:
xt t+( B) t
xt s t

2 趋势平稳过程满足 j 0 j , 所以
xt s lims 0. t
单整序列
差分一次变为平稳过程，记为I(1) 平稳过程记为I(0) 如果差分n-1次不平稳，差分n次平稳，称 为n阶单整的，记为I(n)
趋势平稳过程和单位根过程比较
预测比较
H 0 : xt xt 1 t H1 : xt t ( xt 1 t ) t ,| | 1
包含一个确定性趋势和一个随机趋势
单位根过程
满足下面表达式的过程成为单位根过程
(1 B) xt t 1 t 1
其中

(B) t
(1) 0, j 0 2 j , (u ) 0根在单位圆外.
单位根过程对时间序列的增量进行刻画，增 量平稳，但水平变量不平稳。
2.方差有界并且不随时间变化,是常数. 称为方差齐性
平稳ARMA模型, 可表示为
xt t 1 t 1
,

i 0
| i |
t WN (0, )
2
此类模型的特点 3. 长期预测趋于无条件均值 4. 预测误差的方差有界
序列分解
xt l t l 1 t l 1 et (l )
预测误差
l 1 t 1 l t l 1 t 1 ˆt (l ) x
预测值

ˆ (l ) E ( xt l xt , xt 1 , ) x Var ( xt l xt , xt 1 , ) Var[et (l )]

时间序列分析-第五章非平稳序列的随机分析

【例1.1】1964年——1999年中国纱年产 量序列蕴含着一个近似线性的递增趋势。 对该序列进行一阶差分运算
xt xt xt1
考察差分运算对该序列线性趋势信息的提 取作用
2020/1/4
时间序列分析
差分前后时序图
原序列时序图
差分后序列时序图
2020/1/4
时间序列分析
例5.2
第五章
非平稳序列的随机分析
2020/1/4
时间序列分析
本章结构
差分运算 ARIMA模型 Auto-Regressive模型 异方差的性质 方差齐性变化 条件异方差模型
2020/1/4
时间序列分析
5.1 差分运算
差分运算的实质 差分方式的选择 过差分
2020/1/4
时间序列分析
差分运算的实质
差分方法是一种非常简便、有效的确定 性信息提取方法
Cramer分解定理在理论上保证了适当阶 数的差分一定可以充分提取确定性信息
差分运算的实质是使用自回归的方式提 取确定性信息
d
d xt (1 B)d xt (1)i Cdi xti i0
尝试提取1950年——1999年北京市民用 车辆拥有量序列的确定性信息
2020/1/4
时间序列分析
差分后序列时序图
一阶差分
二阶差分
2020/1/4
时间序列分析
例5.3
差分运算提取1962年1月——1975年12月平均 每头奶牛的月产奶量序列中的确定性信息
2020/1/4
时间序列分析
2020/1/4
时间序列分析
ARIMA模型的平稳性
ARIMA(p,d,q) 模 型 例5.5

时间序列分析--第五章非平稳序列的随机分析

第五章
非平稳序列的随机分析
2020/6/14
课件
1
本章结构
差分运算 ARIMA模型 Auto-Regressive模型 异方差的性质 方差齐性变化 条件异方差模型
2020/6/14
课件
2
5.1 差分运算
差分运算的实质 差分方式的选择 过差分
2020/6/14
课件
3
差分运算的实质
方差大
Var(xt ) Var(at at1)
2 2
Var(2xt ) Var(at 2at1 at2 )
6 2
2020/6/14
课件ቤተ መጻሕፍቲ ባይዱ
14
5.2 ARIMA模型
ARIMA模型结构 ARIMA模型性质 ARIMA模型建模 ARIMA模型预测 疏系数模型 季节模型
2020/6/14
1 1 1 2 1 1 2 2
j 1 j1 pd j pd j
2020/6/14
课件
28
预测值
xtl ( tl 1 tl1 l1 t1) ( l t l1 t1 )
et (l)
xˆt (l)
E[et (l)] 0
Var[et (l)]
(1
2 1
2 l 1
)
2
2020/6/14
课件
29
例5.7
已知ARIMA(1,1,1)模型为
(1 0.8B)(1 B)xt (1 0.6B) t
且 xt1 4.5
xt 5.3
t 0.8
2
1
求 xt3 的95％的置信区间
2020/6/14
课件
30
预测值
等价形式
(11.8B 0.8B2 )xt (1 0.6B)t xt 1.8xt1 0.8xt2 t 0.6t1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

图（1）考虑对该序列进行1阶差分运算，同时考察差分序列的平稳性，在原程序基础上添加相关命令，程序修改如下：图（2）时序图显示差分后序列difx没有明显的非平稳特征。

（2）“identify var=x(1);”，使用该命令可以识别差分后序列的平稳性。

纯随机性和适当的拟合图（6）普通最小二乘估计结果图（8）最终拟合模型输出结果图（9）拟合效果图图（12）带有延迟因变量的回归模型拟合效果图5.8.3拟合GARCH模型SAS系统中AUTOREG过程功能非常强大，不仅可以提供上述的分析功能，还可以提供异方差性检验乃至条件异方差模型建模。

以临时数据集example5_3数据为例，介绍GARCH模型的拟合，相关命令如下：data example5_3;input x@@;t=_n_;cards;10.77 13.30 16.64 19.54 18.97 20.52 24.3623.51 27.16 30.80 31.84 31.63 32.68 34.9033.85 33.09 35.46 35.32 39.94 37.47 35.2433.03 32.67 35.20 32.36 32.34 38.45 38.1732.14 39.70 49.42 47.86 48.34 62.50 63.5667.61 64.59 66.17 67.50 76.12 79.31 78.8581.34 87.06 86.41 93.20 82.95 72.96 61.1061.27 71.58 88.34 98.70 97.31 97.17 91.1780.20 85.12 81.40 70.87 57.75 52.35 67.5087.95 85.46 84.55 98.16 102.42 113.02 119.95122.37 126.96 122.79 127.96 139.20 141.05 140.87137.08 145.53 145.59 134.36 122.54 106.92 97.23110.39 132.40 152.30 154.91 152.69 162.67 160.31142.57 146.54 153.83 141.81 157.83 161.79 142.07139.43 140.92 154.61 172.33 191.78 199.27 197.57189.29 181.49 166.84 154.28 150.12 165.17 170.32;proc gplot data=example5_3;plot x*t=1;symbol1c=black i=join v=start;proc autoreg data=example5_3;model x=t/nlag=5dwprob archtest;model x=t/nlag=2noint garch=(p=1,q=1);output out=out p=p residual=residual lcl=lcl ucl=ucl cev=cev;data out;set out;l95=-1.96*sqrt(51.42515);u95=1.96*sqrt(51.42515);Lcl_GARCH=-1.96*sqrt(cev);Ucl_GARCH=1.96*sqrt(cev);Lcl_p=p-1.96*sqrt(cev);Ucl_p=p+1.96*sqrt(cev);proc gplot data=out;plot residual*t=2 l95*t=3 Lcl_GARCH*t=4 u95*t=3 Ucl_GARCH*t=4/overlay; plot x*t=5 lcl*t=3 LCL_p*t=4 ucl*t=3 UCL_p*t=4/overlay;symbol2c=green i=needle v=none;symbol3v=black i=join c=none w=2l=2;symbol4c=red i=join v=none;symbol5c=green i=join v=none;run;该序列输出时序图如图（13）所示。

图（13）序列时序图时序图显示序列具有显著线性递增趋势，且波动幅度随时间递增，所以考虑使用AUTOREG过程建图（19）残差序列在两种方差假定下的置信区间效果图图（21）序列在两种方差假定下的置信区间效果图图中，中间的波动曲线为残差序列或原序列，虚线为根据无条件方差得到的95%置信区间，而实线为根据条件方差得到的95%置信区间。

习题1data example5_1;input x@@;difx=dif(x);t=_n_;cards;304 303 307 299 296 293 301 293 301 295 284 286 286 287 284282 278 281 278 277 279 278 270 268 272 273 279 279 280 275271 277 278 279 283 284 282 283 279 280 280 279 278 283 278270 275 273 273 272 275 273 273 272 273 272 273 271 272 271273 277 274 274 272 280 282 292 295 295 294 290 291 288 288290 293 288 289 291 293 293 290 288 287 289 292 288 288 285282 286 286 287 284 283 286 282 287 286 287 292 292 294 291288 289;proc gplot;plot x*t;symbol v=star c=black i=join;proc gplot;plot x*t difx*t;symbol v=star c=black i=join;proc arima;identify var=x(1);estimate p=1;forecast lead=5id=t;run;实验结果：图5.1序列时序图由时序图可知该序列不平稳，即该序列为一个非平稳序列。

图5.4预测结果由上图可得，预测1939—1945年英国绵羊的数量分别为1851,1872,1879,1880,1879,1877,1875。

习题六data example5_3;input x@@;t=_n_;lagx=lag(x);cards;4.99 55.03 5.03 5.25 5.26 5.3 5.45 5.49 5.52 5.75.68 5.65 5.86.5 6.45 6.48 6.45 6.35 6.4 6.43 6.436.44 6.45 6.48 6.4 6.35 6.4 6.3 6.32 6.35 6.13 5.75.58 5.18 5.18 5.17 5.15 5.21 5.23 5.05 4.65 4.65 4.64.67 4.69 4.68 4.62 4.63 4.95.44 5.566.04 6.06 6.068.07 8.07 8.1 8.05 8.06 8.07 8.06 8.11 8.6 10.8 1111 11 9.48 9.18 8.62 8.3 8.47 8.44 8.44 8.46 8.498.54 8.54 8.5 8.44 8.49 8.4 8.46 8.5 8.5 8.47 8.478.47 8.48 8.48 8.54 8.56 8.39 8.89 9.91 9.89 9.91 9.919.9 9.88 9.86 9.86 9.74 9.42 9.27 9.26 8.99 8.83 8.838.83 8.82 8.83 8.83 8.79 8.79 8.69 8.66 8.67 8.72 8.779 9.61 9.7 9.94 9.94 9.94 9.95 9.94 9.96 9.97 10.8310.75 11.2 11.4 11.54 11.5 11.34 11.5 11.5 11.58 12.42 12.8513.1 13.12 13.1 13.15 13.1 13.2 14.2 14.75 14.6 14.6 14.4514.5 14.8 15.85 16.2 16.5 16.4 16.4 16.35 16.1 13.7 13.514 12.3 12 14.35 14.6 12.5 12.75 13.7 13.45 13.55 12.612 11 11.6 12.05 12.35 12.7 12.45 12.55 12.2 12.1 11.1511.85 12.1 12.5 12.9 12.5 13.2 13.65 13.65 13.5 13.45 13.35 14.45 14.3 15.05 15.55 15.65 14.65 14.15 13.3 12.65 12.7 12.8 14.5 15.1 15.15 14.3 14.25 14.05 14.7 15.05 14.05 13.8 13.25 13 12.85 12.6 11.8 13 12.35 11.45 11.35 11.55 10.85 10.912.3 11.7 12.05 12.3 12.9 13.05 13.3 13.85 14.65 15.05 15.15 14.85 15.7 15.4 15.1 14.8 15.8 15.8 15 14.4 13.8 14.314.15 14.45 14.1 14.05 13.75 13.3 13 12.55 12.25 11.85 11.511.1 11.15 10.7 10.25 10.55 10.25 10.3 9.6 8.4 8.2 7.25图6.5模型最终拟合结果。