第三章 线性平稳时间序列分析(上海财经大学统计学系 )

线性平稳时间序列分析线性平稳时间序列分析是一种重要的时间序列分析方法，用于研究随时间变化的数据。

它基于一个核心假设，即数据的均值和方差在随时间推移的过程中保持不变。

线性平稳时间序列可以用数学模型来描述，通常使用自回归（AR）模型、滑动平均（MA）模型或自回归滑动平均（ARMA）模型。

这些模型基于该系列在某一时间点的值与该系列在过去时间点的值之间的线性关系。

为了进行线性平稳时间序列分析，首先需要检验数据是否满足平稳性的假设。

常用的检验方法包括ADF检验和单位根检验。

若数据不满足平稳性的假设，则需要通过差分操作将其转化为平稳时间序列。

在得到平稳的时间序列后，可以使用最小二乘法对时间序列进行模型拟合。

通过对数据进行模型拟合，我们可以得到模型的系数以及误差项的信息。

利用这些信息，可以进行时间序列的预测和分析。

在预测方面，线性平稳时间序列分析可以利用过去的观测值来预测未来的值。

预测方法包括简单的移动平均法和指数平滑法，以及更复杂的AR、MA和ARMA模型。

在分析时间序列方面，线性平稳时间序列分析可以通过模型的系数和误差项的信息来揭示数据的特征和规律。

例如，可以用模型的系数来检验是否存在滞后效应，用误差项的信息来检验模型的拟合程度。

总之，线性平稳时间序列分析是一种重要的时间序列分析方法，可以帮助我们研究随时间变化的数据。

通过对数据进行模型拟合、预测和分析，我们可以揭示数据的特征和规律，从而提供决策支持和预测能力。

线性平稳时间序列分析是一种重要的时间序列分析方法，它广泛应用于经济学、金融学、工程学等领域。

该方法基于数据的均值和方差在时间推移过程中保持不变的假设，旨在研究随时间变化的数据及其内在规律，以便进行预测、决策支持和其他分析。

在线性平稳时间序列分析中，首先需要检验数据是否符合平稳性的假设。

平稳性是指数据的均值和方差不随时间变化而发生显著变化。

为了检验平稳性，在实际应用中常常使用单位根检验或ADF检验等方法。

平稳时间序列的统计特征
时间序列是统计学中最重要的概念之
一，它描述了一段时间内变量随时间变化的情况。

平稳时间序列是指变量的均值、方差和自相关系数不随时间变化的时间序列。

平稳时间序列的统计特征是非常重要的，可以帮助我们理解变量的变化特性，并且可以用来对未来变量的变化做出预测。

首先，要确定一个时间序列是否是平稳的，可以使用单位根检验（Unit Root Test）。

如果检验结果表明变量是平稳的，就可以进一步分析它的统计特征。

其次，要了解一个平稳时间序列的统计特征，我们首先要研究它的均值和方差。

均值是描述一个变量的中心位置的指标，而方差是描述变量变化的程度的指标。

如果均值和方差不变，那么这个时间序列就是平稳的。

另外，我们还要研究平稳时间序列的自相关系数。

自相关系数可以衡量相邻变量之间的相关性，它可以用来判断一个时间序列是否是平稳的。

如果这个时间序列的自相关系数是恒定的，那么这个时间序列就是平稳的。

线性平稳时间序列分析线性平稳时间序列分析是统计学中一个重要的研究领域，在经济学、金融学、统计学等领域中具有广泛的应用。

本文将从概念、特征、建模和预测四个方面展开，详细介绍线性平稳时间序列分析的基本内容。

一、概念时间序列是按照时间顺序排列的一组数据观测值的集合，线性平稳时间序列是指其均值、方差和自相关函数在时间上保持不变。

线性平稳时间序列可以用公式表示为：Yt = μ + εt其中，Yt是时间t的观测值，μ是时间序列的均值，εt是时间t的随机波动项。

二、特征线性平稳时间序列具有以下几个重要特征：1. 均值不变性：时间序列的均值在时间上保持不变，即E(Yt) = μ。

2. 方差不变性：时间序列的方差在时间上保持不变，即Var(Yt) = σ^2。

3. 自相关性：时间序列中观测值之间存在相关性，即时间序列的自相关函数具有一定的模式。

4. 白噪声：时间序列中的随机波动项εt是一个均值为零、方差为常数的随机变量。

三、建模线性平稳时间序列的建模是对时间序列数据进行拟合，以寻找其内在的规律和趋势。

常用的线性平稳时间序列模型主要有AR（自回归模型）、MA（移动平均模型）和ARMA（自回归移动平均模型）等。

1. AR模型：自回归模型是基于时间序列在当前时刻与其过去时刻之间存在相关性的假设。

AR模型的阶数p表示过去p个时刻的观测值对当前观测值的影响。

2. MA模型：移动平均模型是基于时间序列在当前时刻与其过去时刻的随机波动项之间存在相关性的假设。

MA模型的阶数q表示过去q个时刻的随机波动项对当前观测值的影响。

3. ARMA模型：自回归移动平均模型是结合了AR模型和MA 模型的特点，既考虑了时间序列观测值的自相关性，又考虑了时间序列随机波动项的相关性。

四、预测线性平稳时间序列的预测是利用已有的时间序列数据预测未来的观测值。

常用的线性平稳时间序列预测模型主要有AR、MA和ARMA等。

1. AR模型：通过对过去p个时刻的观测值进行线性组合，预测当前观测值。

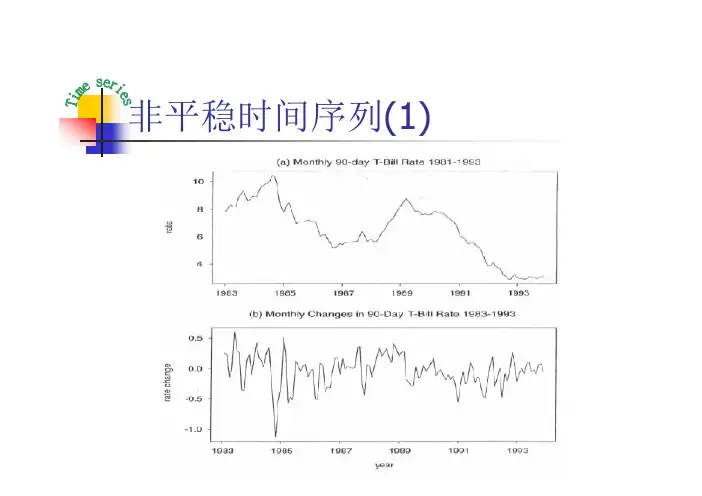
平稳时间序列分析平稳时间序列分析是一种常用的时间序列分析方法，它旨在研究时间序列在均值和方差上的稳定性，并将其用于预测未来的数据走势。

本文将详细介绍平稳时间序列分析的基本概念、建模方法和预测技术。

首先，让我们来了解什么是时间序列。

时间序列是按照一定的时间间隔收集到的一系列数据点的有序集合，它可以是连续的或离散的。

时间序列分析的目的是通过对过去的数据进行统计分析，揭示出时间序列中的内在规律和趋势，并预测未来的数据走势。

平稳时间序列是指在统计意义上具有稳定性的时间序列，即其均值和方差保持恒定不变。

平稳时间序列具有以下特点：1）均值是常数，不随时间变化；2）方差是常数，不随时间变化；3）协方差只与时间间隔有关，与具体的时间点无关。

为了实现平稳时间序列分析，我们需要进行以下几个步骤：1. 数据准备：收集所需的时间序列数据，并将其整理成适合分析的格式。

通常，我们会绘制时间序列图以直观地查看数据的趋势和模式。

2. 时间序列分解：时间序列通常包含趋势、季节性和随机成分。

我们需要对时间序列进行分解，将其分解为这些组成部分。

常用的分解方法有经典的加性模型和乘性模型。

3. 平稳性检验：对于时间序列分析，我们需要确保数据是平稳的。

平稳性检验的目的是判断时间序列的均值和方差是否是稳定的。

常用的平稳性检验方法有ADF检验、KPSS检验等。

4. 模型建立：如果时间序列被证实是平稳的，我们可以根据数据的模式和趋势选择适当的模型。

常用的模型包括自回归滑动平均模型（ARMA模型）、自回归积分滑动平均模型（ARIMA模型）等。

5. 模型识别与估计：在模型建立的基础上，我们需要对模型进行识别和估计。

模型识别的目的是选择最适合数据的模型阶数，常用的方法有自相关函数（ACF）和偏自相关函数（PACF）的分析。

模型的估计通常使用最大似然估计方法。

6. 模型检验：建立模型后，我们需要对模型进行检验，验证其拟合程度和预测准确度。

常用的模型检验方法有残差分析、DW检验、Ljung-Box检验等。

应用时间序列分析实验报告实验名称第三章平稳时间序列分析一、上机练习data example3_1;input x;time=_n_;cards;;proc gplot data=example3_1;plot xtime=1;symbol c=red i=join v=star;run;建立该数据集,绘制该序列时序图得：根据所得图像,对序列进行平稳性检验;时序图就是一个平面二维坐标图,通常横轴表示时间,纵轴表示序列取值;时序图可以直观地帮助我们掌握时间序列的一些基本分布特征;根据平稳时间序列均值、方差为常数的性质,平稳序列的时序图应该显示出该序列始终在一个常数值附近随机波动,而且波动的范围有界的特点;如果观察序列的时序图,显示出该序列有明显的趋势性或周期性,那它通常不是平稳序列;从图上可以看出,数值围绕在0附近随机波动,没有明显或周期,其本可以视为平稳序列,时序图显示该序列波动平稳;proc arima data=example3_1;identify var=x nlag=8;run;图一图二样本自相关图图三样本逆自相关图图四样本偏自相关图图五纯随机检验图实验结果分析：1由图一我们可以知道序列样本的序列均值为,标准差为,观察值个数为84个;2根据图二序列样本的自相关图我们可以知道该图横轴表示自相关系数,综轴表示延迟时期数,用水平方向的垂线表示自相关系数的大小;我们发现样本自相关图延迟3阶之后,自相关系数都落入2倍标准差范围以内,而且自相关系数向衰减的速度非常快,延迟5阶之后自相关系数即在值附近波动;这是一个短期相关的样本自相关图;所以根据样本自相关图的相关性质,可以认为该序列平稳;3根据图五的检验结果我们知道,在各阶延迟下LB检验统计量的P值都非常小<,所以我们可以以很大的把握置信水平>%断定该序列样本属于非白噪声序列;proc arima data=example3_1;identify var=x nlag=8minic p= 0:5q=0:5;run;IDENTIFY命令输出的最小信息量结果某个观察值序列通过序列预处理,可以判定为平稳非白噪声序列,就可以利用ARMA模型对该序列建模;建模的基本步骤如下：A：求出该观察值序列的样本自相关系数ACF和样本偏自相关系数PACF的值;B：根据样本自相关系数和偏自相关系数的性质,选择适当地ARMAp,q模型进行拟合;C：估计模型中未知参数的值;D：检验模型有效性;如果拟合模型不通过检验,转向步骤B,重新选择模型再拟合;E：模型优化;如果拟合模型通过检验,仍然转向步骤B,充分考虑各种可能,建立多个拟合模型,从所有通过检验中选择最优模型;F：利用拟合模型,预测序列的将来走势;为了尽量避免因个人经验不足导致的模型识别问题,SAS系统还提供了相对最优模型识别;最后一条信息显示,在自相关延迟阶数小于等于5,移动平均延迟阶数也小于等于5的所有ARMRp,q模型中,BIC信息量相对最小的是ARMR0,4模型,即MA4模型;需要注意的是,MINIC只给出一定范围内SBC最小的模型定阶结果,但该模型的参数未必都能通过参数检验,即经常会出现MINIC给出的模型阶数依然偏高的情况;estimate q=4;run;本例参数估计输出结果显示均值MU不显著t的检验统计量的P值为,其他参数均显著t检验统计量的P值均小于,所以选择NOINT选项,除去常数项,再次估计未知参数的结果,即可输入第二条ESTIMATE 命令：estimate q=4 noint;run;参数估计部分输出结果如图六所示：图六ESTIMATE命令消除常数项之后的输出结果显然四个未知参数均显著;拟合统计量的值这部分输出五个统计量的值,由上到下分别是方差估计值、标准差估计值、AIC信息量、SBC信息量及残差个数,如图七所示：图七ESTIMATE命令输出的拟合统计量的值系数相关阵这部分输出各参数估计值的相关阵,如图八所示：图八ESTIMATE命令输出的系数相关阵残差自相关检验结果这部分的输出格式图九和序列自相关系数白噪声检验部分的输出结果一样;本例中由于延迟各阶的LB统计量的P值均显著大于aa=,所以该拟合模型显著成立;图九ESTIMATE命令输出的残差自相关检验结果拟合模型的具体形式ESTIMA TE命令输出的拟合模型的形式序列预测forecast lead=5id=time out=results;run;其中,lead是指定预测期数；id是指定时间变量标识；out是指定预测后的结果存入某个数据集;该命令运行后输出结果如下：FORECAST命令输出的预测结果该输出结果从左到右分别为序列值的序号、预测值、预测值的标准差、95%的置信下限、95%的置信上限;利用存储在临时数据集RESULTS里的数据,我们还可以绘制漂亮的拟合预测图,相关命令如下：proc gplot data=results;plot xtime=1 forecasttime=2 l95time=3 u95time=3/overlay;symbol1c=black i=none v=start;symbol2c=red i=join v=none;symbol3c=green i=join v=none l=32;run;输出图像如下：拟合效果图注：图中,S号代表序列的观察值；连续曲线代表拟合序列曲线；虚线代表拟合序列的95%上下置信限;所谓预测就是要利用序列以观察到的样本值对序列在未来某个时刻的取值进行估计;目前对平稳序列最常用的预测方法是线性最小方差预测;线性是指预测值为观察值序列的线性函数,最小方差是指预测方差达到最小;在预测图上可以看到,数据围绕一个范围内波动,即说明未来的数值变化时平稳的;二、课后习题第十七题：根据某城市过去63年中每年降雪量数据单位：mm得：书本P94程序：data example17_1;input x;time=_n_;cards;2579588397 110;proc gplot data=example17_1;plot xtime=1;symbol c=red i=join v=star;run;proc arima data=example17_1;identify var=x nlag=15minic p= 0:5q=0:5;run;estimate p=1;run;estimate p=1 noin;run;forecast lead=5id=time out=results;run;proc gplot data=results;plot xtime=1 forecasttime=2 l95time=3 u95time=3/overlay;symbol1c=black i=none v=start;symbol2c=red i=join v=none;symbol3c=green i=join v=none l=32;run;1判断该序列的平稳性与纯随机性该序列的时序图如下图a图a由时序图显示过去63年中每年降雪量数据围绕早70mm附近随机波动,没有明显趋势或周期,基本可以看成平稳序列,为了稳妥起见,做了如下自相关图图b图b时序图就是一个平面二维坐标图,通常横轴表示时间,纵轴表示序列取值;时序图可以直观地帮助我们掌握时间序列的一些基本分布特征;根据平稳时间序列均值、方差为常数的性质,平稳序列的时序图应该显示出该序列始终在一个常数值附近随机波动,而且波动的范围有界的特点;如果观察序列的时序图,显示出该序列有明显的趋势性或周期性,那它通常不是平稳序列;样本的自相关图我们可以知道该图横轴表示自相关系数,综轴表示延迟时期数,用水平方向的垂线表示自相关系数的大小;我们发现样本自相关图延迟2阶之后,自相关系数都落入2倍标准差范围以内, 自相关图显示该序列自相关系数一直都比较小,1阶开始控制在2倍的标准差范围以内,可以认为该序列自始自终都在零轴附近波动,这是随即性非常强的平稳时间序列;纯随机性检验见下图：图c图c根据图c的检验结果我们知道,在6阶延迟下LB检验统计量的P值显著小于,所以我们可以以很大的把握置信水平>95%断定这个拟合模型的残差序列属于非白噪声序列;2如果序列平稳且非白躁声,选择适当模型拟合该序列的发展;模型识别如下图图d图d假如某个观察值序列通过序列预处理,可以判定为平稳非白噪声序列,就可以利用ARMA模型对该序列建模;建模的基本步骤如下：1：求出该观察值序列的样本自相关系数ACF和样本偏自相关系数PACF的值;2：根据样本自相关系数和偏自相关系数的性质,选择适当地ARMAp,q模型进行拟合;3：估计模型中未知参数的值;4：检验模型有效性;如果拟合模型不通过检验,转向步骤B,重新选择模型再拟合;5：模型优化;如果拟合模型通过检验,仍然转向步骤B,充分考虑各种可能,建立多个拟合模型,从所有通过检验中选择最优模型;6：利用拟合模型,预测序列的将来走势;最后一条信息显示,在自相数迟阶数小于等于5,移动平均延迟阶数也小于等于5的所有ARMAp,q模型中,BIC信息量相对最小的是ARMA1,0模型,既AR1模型;它们的自相关系数都呈现出拖尾性和呈指数衰减到零值附近的性质;自相关系数是按负指数单调收敛到零；利用拟合模型,预测该城市未来5年的降雪量.由2可以知道该模型是AR1模型；预测结果如下图图e由图得未来564-68年的降雪量分别为、、、、;18. 某地区连续74年的谷物产量单位：千吨data example18_1;input x;time=_n_;cards;;proc gplot data=example18_1;plot xtime=1;symbol c=red i=join v=star;run;proc arima data=example18_1;identify var=x nlag=18minic p= 0:5q=0:5;run;estimate q=1;run;forecast lead=5id=time out=results;run;proc gplot data=results;plot xtime=1 forecasttime=2 l95time=3 u95time=3/overlay; symbol1c=black i=none v=start;symbol2c=red i=join v=none;symbol3c=green i=join v=none l=32;run;1判断该序列的平稳性与纯随机性该序列的时序图如下图f图f时序图就是一个平面二维坐标图,通常横轴表示时间,纵轴表示序列取值;时序图可以直观地帮助我们掌握时间序列的一些基本分布特征;根据平稳时间序列均值、方差为常数的性质,平稳序列的时序图应该显示出该序列始终在一个常数值附近随机波动,而且波动的范围有界的特点;如果观察序列的时序图,显示出该序列有明显的趋势性或周期性,那它通常不是平稳序列;由时序图显示过去74年中每年谷物产量数据围绕早千吨附近随机波动,没有明显趋势或周期,基本可以看成平稳序列,为了稳妥起见,做了如下自相关图图g图g样本的自相关图我们可以知道该图横轴表示自相关系数,综轴表示延迟时期数,用水平方向的垂线表示自相关系数的大小;我们发现样本自相关图延迟2阶之后,自相关系数都落入2倍标准差范围以内,自相关图显示该序列自相关系数一直都比较小,1阶开始控制在2倍的标准差范围以内,可以认为该序列自始自终都在零轴附近波动,这是随即性非常强的平稳时间序列;纯随机性检验见下图：图h图h根据图h的检验结果我们知道,在各阶延迟下LB检验统计量的P值显著小于,所以我们可以以很大的把握置信水平>95%断定这个拟合模型的残差序列属于非白噪声序列;选择适当模型拟合该序列的发展;如果序列平稳且非白躁声,选折适当模型拟合序列的发展模型识别如下图图i图i假如某个观察值序列通过序列预处理,可以判定为平稳非白噪声序列,就可以利用ARMA模型对该序列建模;建模的基本步骤如下：A：求出该观察值序列的样本自相关系数ACF和样本偏自相关系数PACF的值;B：根据样本自相关系数和偏自相关系数的性质,选择适当地ARMAp,q模型进行拟合;C：估计模型中未知参数的值;D：检验模型有效性;如果拟合模型不通过检验,转向步骤B,重新选择模型再拟合;E：模型优化;如果拟合模型通过检验,仍然转向步骤B,充分考虑各种可能,建立多个拟合模型,从所有通过检验中选择最优模型;F：利用拟合模型,预测序列的将来走势;最后一条信息显示,在自相数迟阶数小于等于5,移动平均延迟阶数也小于等于5的所有ARMAp,q模型中,BIC信息量相对最小的是ARMA1,0模型,既AR1模型;它们的自相关系数都呈现出拖尾性和呈指数衰减到零值附近的性质;自相关系数是按负指数单调收敛到零；利用拟合模型,预测该地区未来5年的谷物产量,预测结果如下图图j 由2可知,该模型为AR1模型；图j未来5年的谷物产量一次为,,,;19. 现有201个连续的生产记录data example19_1;input x;time=_n_;cards;图l时序图就是一个平面二维坐标图,通常横轴表示时间,纵轴表示序列取值;时序图可以直观地帮助我们掌握时间序列的一些基本分布特征;根据平稳时间序列均值、方差为常数的性质,平稳序列的时序图应该显示出该序列始终在一个常数值附近随机波动,而且波动的范围有界的特点;如果观察序列的时序图,显示出该序列有明显的趋势性或周期性,那它通常不是平稳序列;样本的自相关图我们可以知道该图横轴表示自相关系数,综轴表示延迟时期数,用水平方向的垂线表示自相关系数的大小;我们发现样本自相关图延迟1阶之后,自相关系数都落入2倍标准差范围以内, 自相关图显示该序列自相关系数一直都比较小,1阶开始控制在2倍的标准差范围以内,可以认为该序列自始自终都在零轴附近波动,这是随即性非常强的平稳时间序列;纯随机性检验见下图：图m根据图m的检验结果我们知道,在各阶延迟下LB检验统计量的P值显著小于,所以我们可以以很大的把握置信水平>95%断定这个拟合模型的残差序列属于非白噪声序列;2如果序列平稳且非白躁声,选折适当模型拟合序列的发展模型识别如下图图n某个观察值序列通过序列预处理,可以判定为平稳非白噪声序列,就可以利用ARMA模型对该序列建模;建模的基本步骤如下：1、求出该观察值序列的样本自相关系数ACF和样本偏自相关系数PACF的值;2、根据样本自相关系数和偏自相关系数的性质,选择适当地ARMAp,q模型进行拟合;3、估计模型中未知参数的值;4、检验模型有效性;如果拟合模型不通过检验,转向步骤B,重新选择模型再拟合;5、模型优化;如果拟合模型通过检验,仍然转向步骤B,充分考虑各种可能,建立多个拟合模型,从所有通过检验中选择最优模型;6、利用拟合模型,预测序列的将来走势;最后一条信息显示,在自相数迟阶数小于等于5,移动平均延迟阶数也小于等于5的所有ARMAp,q模型中,BIC信息量相对最小的是ARMA0,1模型,即MA1模型;利用拟合模型,预测该城市下一时刻95%的置信区间;由2可得,该模型为MA1模型；下一时刻95%的置信区间,;实验小结：给定一个序列,我们首先应该判断平稳性,如果平稳,再检查是否是纯随机序列,如果序列平稳且非白躁声,选折适当模型拟合序列的发展,选择AR,MA,或ARMA模型,然后可以对该序列进行预测;三、实验体会通过本次实验使我掌握了一些对时间序列的处理,运用不同的语句对一个样本序列的平稳性检验和随机性检验,这对我们处理数据有很大的帮助;在生活中我们往往会遇到这样的现象,当我们所得到的样本信息太少,并且没有其他的辅助信息时,通常这种数据结构式没法进行分析的,但是序列平稳性的概念的提。

欢迎共阅t P p t tt t t x B x x B x Bx x ===---221第3章 平稳时间序列分析一个序列经过预处理被识别为平稳非白噪声序列，那就说明该序列是一个蕴含着相关信息的平稳序列。

3.1 方法性工具 3.1.1 差分运算 一、p 阶差分记t x ∇为t x 的1阶差分：1--=∇t t t x x x记t x 2∇为t x 的2阶差分：21122---+-=∇-∇=∇t t t t t t x x x x x x 以此类推：记t p x ∇为t x 的p 阶差分：111---∇-∇=∇t p t p t p x x x 二、k 步差分记t k x ∇为t x 的k 步差分：k t t t k x x x --=∇3.1.2 延迟算子 一、定义延迟算子相当与一个时间指针，当前序列值乘以一个延迟算子，就相当于把当前序列值的时间向过去拨了一个时刻。

记B 为延迟算子，有延迟算子的性质：1.10=B2.若c 为任一常数，有1)()(-⋅=⋅=⋅t t t x c x B c x c B3.对任意俩个序列{t x }和{t y }，有11)(--±=±t t t t y x y x B4.n t t n x x B -=5.)!(!!,)1()1(0i n i n C B C B in i i nni i n-=-=-∑=其中二、用延迟算子表示差分运算 1、p 阶差分 2、k 步差分3.2 ARMA 模型的性质 3.2.1 AR 模型定义 具有如下结构的模型称为p 阶自回归模型，简记为AR(p):ts Ex t s E Var E x x x x t s t s t t p tp t p t t t ∀=≠===≠+++++=---,0,0)(,)(,0)(,0222110εεεσεεφεφφφφε(3.4)AR(p)模型有三个限制条件：条件一：0≠p φ。

这个限制条件保证了模型的最高阶数为p 。