第二章平稳时间序列分析

《时间序列分析》习题解答�0�2习题2.3�0�21考虑时间序列12345…201判断该时间序列是否平稳2计算该序列的样本自相关系数kρ∧k12… 6 3绘制该样本自相关图并解释该图形. �0�2解1根据时序图可以看出该时间序列有明显的递增趋势所以它一定不是平稳序列�0�2即可判断该时间序是非平稳序列其时序图程序见后。

�0�2 时间序描述程序data example1 input number timeintnxyear01jan1980d _n_-1 format time date. cards 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 proc gplot dataexample1 plot numbertime1 symbol1 cblack vstar ijoin run�0�2�0�2�0�22当延迟期数即k本题取值1 2 3 4 5 6远小于样本容量n本题为20时自相关系数kρ∧计算公式为number1234567891011121314151617181920time01JAN8001J AN8101JAN8201JAN8301JAN8401JAN8501JAN8601JAN870 1JAN8801JAN8901JAN9001JAN9101JAN9201JAN9301JAN9 401JAN9501JAN9601JAN9701JAN9801JAN99121nkttktknttX XXXXXρ�6�1∧�6�1�6�1≈�6�1∑∑ 0kn4.9895�0�2注20.05125.226χ接受原假设认为该序列为纯随机序列。

�0�2解法三、Q统计量法计算Q统计量即12214.57kkQnρ∑�0�2�0�2�0�2�0�2�0�2�0�2�0�2�0�2�0�2�0�2查表得210.051221.0261χ�6�1由于Q统计量值4.57Q小于查表临界值即可认为接受原假设即该序列可视为纯随机序列为白噪声序列 5表2——9数据是某公司在2000——2003年期间每月的销售量。

线性平稳时间序列分析线性平稳时间序列分析是一种重要的时间序列分析方法，用于研究随时间变化的数据。

它基于一个核心假设，即数据的均值和方差在随时间推移的过程中保持不变。

线性平稳时间序列可以用数学模型来描述，通常使用自回归（AR）模型、滑动平均（MA）模型或自回归滑动平均（ARMA）模型。

这些模型基于该系列在某一时间点的值与该系列在过去时间点的值之间的线性关系。

为了进行线性平稳时间序列分析，首先需要检验数据是否满足平稳性的假设。

常用的检验方法包括ADF检验和单位根检验。

若数据不满足平稳性的假设，则需要通过差分操作将其转化为平稳时间序列。

在得到平稳的时间序列后，可以使用最小二乘法对时间序列进行模型拟合。

通过对数据进行模型拟合，我们可以得到模型的系数以及误差项的信息。

利用这些信息，可以进行时间序列的预测和分析。

在预测方面，线性平稳时间序列分析可以利用过去的观测值来预测未来的值。

预测方法包括简单的移动平均法和指数平滑法，以及更复杂的AR、MA和ARMA模型。

在分析时间序列方面，线性平稳时间序列分析可以通过模型的系数和误差项的信息来揭示数据的特征和规律。

例如，可以用模型的系数来检验是否存在滞后效应，用误差项的信息来检验模型的拟合程度。

总之，线性平稳时间序列分析是一种重要的时间序列分析方法，可以帮助我们研究随时间变化的数据。

通过对数据进行模型拟合、预测和分析，我们可以揭示数据的特征和规律，从而提供决策支持和预测能力。

线性平稳时间序列分析是一种重要的时间序列分析方法，它广泛应用于经济学、金融学、工程学等领域。

该方法基于数据的均值和方差在时间推移过程中保持不变的假设，旨在研究随时间变化的数据及其内在规律，以便进行预测、决策支持和其他分析。

在线性平稳时间序列分析中，首先需要检验数据是否符合平稳性的假设。

平稳性是指数据的均值和方差不随时间变化而发生显著变化。

为了检验平稳性，在实际应用中常常使用单位根检验或ADF检验等方法。

第⼆章平稳时间序列模型——ACF和PACF和样本ACFPACF⾃相关函数/⾃相关曲线ACFAR(1)模型的ACF：模型为：当其满⾜平稳的必要条件|a1|<1时（所以说，⾃相关系数是在平稳条件下求得的）：y(t)和y(t-s)的⽅差是有限常数，y(t)和y(t-s)的协⽅差伽马s除以伽马0，可求得ACF如下：由于{rhoi}其在平稳条件|a1|<1下求得，所以平稳0<a1<1则⾃相关系数是直接收敛到0-1<a1<0则⾃相关系数是震荡收敛到0对于AR(2)模型的ACF：（略去截距项）两边同时乘以y(t)，y(t-1)，y(t-2)......得到yule-Walker⽅程，然后结合平稳序列的⼀些性质（yule-Walker⽅程法确确实实⽤了协⽅差只与时间间隔有关的性质），得到⾃相关系数如下：rho0恒为1（⼆阶差分⽅程）令⼈惊喜的是，这个⼆阶差分⽅程的特征⽅程和AR(2)模型的是⼀致的。

所以，我们的rho本就是在序列平稳的条件下求得，所以{rhoi}序列也平稳。

当然，其收敛形式取决于a1和a2MA(1)模型的ACF:模型为：由于y(t)的表达式是由⽩噪声序列中的项组成，所以不需要什么平稳条件，就可以求得rho的形式如下：对于MA(p)模型，rho(p+1)开始，之后都为0.所以说，到了p阶之后突然阶段，变为0了。

ARMA(1,1)模型的ACF：模型为：还是使⽤yule-Walker⽅程法（⽤到了序列平稳则协⽅差只与时间间隔有关的性质）得到：所以有：ARMA(p,q)模型的ACF：ARMA(p,q)的⾃相关系数满⾜：（式1）前p个rho值（rho1，rho2...rhop）可以看做yule-Walker⽅程的初始条件，其他滞后值取决于特征⽅程。

（其实是这样的，rho1，rho2...rhop实际上能写出⼀个表达式，⽽rho(p+1)开始，就满⾜⼀个差分⽅程，⽽这个⽅程对应的特征根（即式1）⽅程和AR(p)对应的⼀模⼀样），所以，他会从之后q期开始衰减。

趋势平稳的的时间序列趋势平稳的时间序列是指在一段时间内，其数据呈现出相对稳定的发展趋势，即没有明显的上升或下降趋势。

在统计学中，趋势平稳的时间序列对于分析和预测具有重要意义。

趋势平稳的时间序列的特征主要有以下几个方面：1. 均值稳定性：趋势平稳的时间序列的均值在不同的时间段内保持相对稳定。

也就是说，数据的整体平均水平没有明显的增长或降低趋势。

2. 方差稳定性：趋势平稳的时间序列的方差在不同时间段内保持相对稳定。

也就是说，数据的波动性没有明显的增加或减少趋势。

3. 自相关性：趋势平稳的时间序列的不同时刻的观测值之间存在一定的自相关性。

也就是说，当前时刻的观测值与前一时刻（或者前几个时刻）的观测值相关联。

这种自相关性是由于时间序列中的某种内在规律性或者周期性导致的。

4. 缺乏季节性或周期性：趋势平稳的时间序列在一段时间内不具备明显的季节性或周期性变化。

也就是说，数据的变化主要是由整体趋势所引起的，而非季节性或周期性因素所导致。

趋势平稳的时间序列分析和预测相对比较简单，因为在其基础上可以应用一些经典的时间序列分析方法。

以下是几种常见的分析和预测方法：1. 移动平均法：移动平均法是一种通过计算相邻时间段内的数据均值来平滑时间序列的方法。

在趋势平稳的时间序列中，由于数据的整体趋势相对稳定，因此移动平均法可以有效降低数据的随机波动，提取出数据的主要趋势，从而更好地分析和预测。

2. 指数平滑法：指数平滑法是一种通过加权平均计算当前时刻的观测值的方法，其中对不同时刻的观测值赋予不同的权重。

在趋势平稳的时间序列中，指数平滑法可以根据当前时刻的观测值和先前时刻的预测值来计算最新的预测值，从而更好地捕捉到数据的趋势性。

3. 自回归移动平均模型(ARIMA)：ARIMA模型是一种常用的时间序列模型，可以将时间序列分解为自回归(AR)部分、差分(I)部分和滑动平均(MA)部分。

在趋势平稳的时间序列中，ARIMA模型可以通过拟合数据的自回归部分和滑动平均部分来进行预测，从而更好地反映数据的整体趋势。

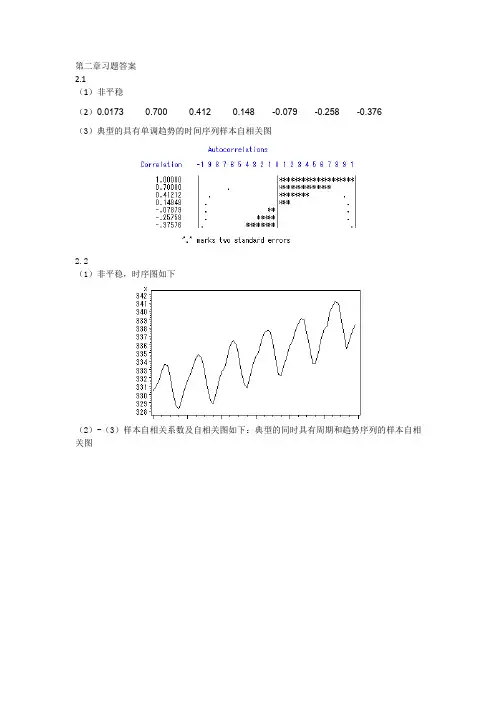
第二章习题答案2.1（1）非平稳（2）0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376（3）典型的具有单调趋势的时间序列样本自相关图2.2（1）非平稳，时序图如下（2）-（3）样本自相关系数及自相关图如下：典型的同时具有周期和趋势序列的样本自相关图2.3（1）自相关系数为：0.2023 0.013 0.042 -0.043 -0.179 -0.251 -0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070 -0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062 -0.139 -0.034 0.206 -0.010 0.080 0.118（2）平稳序列（3）白噪声序列2.4，序列LB=4.83，LB统计量对应的分位点为0.9634，P值为0.0363。

显著性水平=0.05不能视为纯随机序列。

2.5（1）时序图与样本自相关图如下（2） 非平稳 （3）非纯随机 2.6（1）平稳，非纯随机序列（拟合模型参考：ARMA(1,2)） （2）差分序列平稳，非纯随机第三章习题答案3.1 解：1()0.7()()t t t E x E x E ε-=⋅+0)()7.01(=-t x E 0)(=t x E t t x ε=-）B 7.01(t t t B B B x εε)7.07.01()7.01(221Λ+++=-=- 229608.149.011)(εεσσ=-=t x Var49.00212==ρφρ 022=φ3.2 解：对于AR （2）模型：⎩⎨⎧=+=+==+=+=-3.05.02110211212112011φρφρφρφρρφφρφρφρ 解得：⎩⎨⎧==15/115/721φφ3.3 解：根据该AR(2)模型的形式，易得：0)(=t x E原模型可变为：t t t t x x x ε+-=--2115.08.02212122)1)(1)(1(1)(σφφφφφφ-+--+-=t x Var2)15.08.01)(15.08.01)(15.01()15.01(σ+++--+==1.98232σ⎪⎩⎪⎨⎧=+==+==-=2209.04066.06957.0)1/(1221302112211ρφρφρρφρφρφφρ ⎪⎩⎪⎨⎧=-====015.06957.033222111φφφρφ 3.4 解：原模型可变形为：t t x cB B ε=--)1(2由其平稳域判别条件知：当1||2<φ，112<+φφ且112<-φφ时，模型平稳。

时间序列分析习题解答第二章 P.33 2.3 习 题2.4 若序列长度为100，前12个样本自相关系数如下：1^ρ=0.02 2^ρ=0.05 3^ρ=0.10 4^ρ=-0.02 5^ρ=0.05 6^ρ=0.01 7^ρ=0.12 8^ρ=-0.06 9^ρ=0.08 10^ρ=-0.05 11^ρ=0.02 12^ρ=-0.05该序列能否视为纯随机序列？ 解：假设 12210H ρρρ=== ：：1H 至少存在某个12k 10k ≤≤≠，ρ计算Q 统计量: 21ˆm k k Q n ρ==∑, ∑=-∧+=mk kn kn n LB 12)2(ρ其中n 为序列长度100，12m =，(1,2,,12)k k ρ=…为12个样本自相关系数。

计算得到： 4.57Q =， LB=4.99查表得：975.0)1212P 23.51240.4122975.02295.02975.0=>==）（）（（）（，）（χχχχ 因为 4.57Q =与LB=4.99 均介于4.40与5，23之间，故P 值约为0.96，显著大于显著性水平0.05。

所以不能拒绝纯随机的原假设，可以认为该序列为白噪声序列，即认为该序列为纯随机序列。

（注：计算在EXCEL 中进行）2.5 下表数据是某公司在2000-2003年期间每月的销售量。

——————————————————————————— 月份 2000年 2001年 2002年 2003年 1月 153 134 145 117 2月 187 175 203 178 3月 234 243 189 149 4月 212 227 214 178 5月 300 298 295 248 6月 221 256 220 202 7月 201 237 231 162 8月 175 165 174 1359月 123 124 119 12010月 104 106 85 9611月 85 87 67 9012月 78 74 75 63 —————————————————————————————（1）绘制该序列时序图及样本自相关图；（2）判断该序列的平稳性；（3）判断该序列的纯随机性。

时间序列分析习题解答第二章 P.33 2.3 习 题2.1 考虑序列{1，2，3，4，5，…，20}： (1) 判断该序列是否平稳；(2) 计算该序列的样本自相关系数k ^ρ(k=1,2,…,6); (3) 绘制该样本自相关图，并解释该图形。

解：(1) 由于不存在常数μ，使,t EX t T μ=∀∈，所以该序列不是平稳序列。

显然，该序列是按等步长1单调增加的序列。

(2) 1^ρ=0.85000 2^ρ=0.70150 3^ρ=0.556024^ρ=0.41504 5^ρ=0.28008 6^ρ=0.15263 (3) 样本自相关图该图横轴表示自相关系数，纵轴表示延迟时期数。

该图的自相关系数递减的速度缓慢，在6期的延迟时期里，自相关系数一直为正，说明该序列是有单调趋势的非平稳序列。

附：SAS 程序如下： data ex2_1; input freq@@; cards;1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 ;proc arima data=ex2_1; identify var=freq Nlag=6; run;可得到上图的自相关图等内容, 更多结果被省略。

2.2 1975-1980年夏威夷岛莫那罗亚火山（Mauna Loa ）每月释放的CO 2数据如下（单位：ppm ）见下表。

330.45 330.97 331.64 332.87 333.61 333.55 331.90 330.05 328.58 328.31 329.41 330.63 331.63 332.46 333.36 334.45 334.82 334.32 333.05 330.87 329.24 328.87 330.18 331.50 332.81 333.23 334.55 335.82 336.44 335.99 334.65 332.41 331.32 330.73 332.05 333.53 334.66 335.07 336.33 337.39 337.65 337.57 336.25 334.39 332.44 332.25 333.59 334.76 335.89 336.44 337.63 338.54 339.06 338.95 337.41 335.71 333.68 333.69 335.05 336.53 337.81 338.16 339.88 340.57 341.19 340.87 339.25 337.19 335.49 336.63 337.74 338.36（1）绘制该序列时序图，并判断该序列是否平稳； （2）计算该序列的样本自相关系数k ^(k=1,2,…,24); （3）绘制该样本自相关图，并解释该图形。

平稳的时间序列满足的三个条件平稳时间序列是指其统计特征在时间移动中保持恒定的一类时间序列。

平稳性是时间序列分析中最基本、最重要的概念之一，对于理解和预测时间序列数据具有重要意义。

平稳时间序列的分析方法可以用于经济、金融、自然科学、社会科学等领域的研究。

平稳时间序列满足的三个条件是：1.均值不随时间变化：平稳时间序列的均值在时间移动中保持不变。

即在序列的任意一段时间内，该段时间的均值与整个序列的均值相等。

这意味着序列的总体趋势不随时间发生变化，可以看作是一个平稳的随机过程。

2.方差不随时间变化：平稳时间序列的方差在时间移动中保持不变。

方差是描述序列数据波动性大小的度量，如果方差不随时间变化，则说明序列的波动性保持稳定，不会随着时间的推移而发生明显的变化。

3.自协方差不随时间变化：平稳时间序列的自协方差在时间移动中保持不变。

自协方差是描述时间序列自身之间相关性的度量，如果自协方差不随时间变化，则说明序列的内部相关性保持稳定，序列中的观测值之间的相关性不会随着时间的推移而发生明显的变化。

这三个条件合起来就构成了平稳时间序列的基本特征，也被称为严平稳性。

如果一个时间序列不满足以上条件，我们称其为非平稳时间序列。

为了更加形象地理解平稳时间序列的概念，可以举一个例子来说明。

假设我们对某商店的每日销售额进行观察，我们可以假设这个时间序列是平稳的。

如果这个商店的每日销售额持续增长，那么这个时间序列就不满足平稳性的第一个条件，即均值不随时间变化。

同样，如果商店的销售额的波动性在时间推移中发生变化，那么这个时间序列就不满足平稳性的第二个条件，即方差不随时间变化。

另外，如果商店的销售额与前一天的销售额相关性在时间推移中发生变化，那么这个时间序列就不满足平稳性的第三个条件，即自协方差不随时间变化。

在实际应用中，对平稳时间序列的研究有助于我们理解序列的规律和特征，进而可以对未来的数据进行预测和决策。

平稳时间序列的分析方法包括自回归移动平均（ARMA）模型、自回归集成滑动平均（ARIMA）模型、指数平滑模型等。

第⼆章平稳时间序列模型——AR（p）,MA（q）,ARMA（p,q）模型及其平稳性1⽩噪声过程:零均值，同⽅差，⽆⾃相关（协⽅差为0）以后我们遇到的efshow如果不特殊说明，就是⽩噪声过程。

对于正态分布⽽⾔，不相关即可推出独⽴，所以如果该⽩噪声如果服从正态分布，则其还将互相独⽴。

2各种和模型p阶移动平均过程：q阶⾃回归过程：⾃回归移动平均模型：如果ARMA(p,q)模型的表达式的特征根⾄少有⼀个⼤于等于1，则{y(t)}为积分过程，此时该模型称为⾃回归秋季移动平均模型（ARIMA）时间序列啊，不就是求个通项公式，然后求出⼀个⾮递推形式的表达式吗？（这个公式和⾃变量t有关，然后以后只要知道t就能得到对应的y的预测值）3弱平稳/协⽅差平稳：均值和⽅差为常数（即同⽅差），协⽅差仅与时间间隔有关4⾃相关系数：5AR(1)模型（带⽩噪声的⼀阶差分⽅程）的平稳性：（1）如果初始条件为y0：则其解为（我们通过其解来判断其是否平稳）此时{y(t)}是不平稳的。

· 但是如果|a1|<1，其t⾜够⼤，则{y(t)}是平稳的。

均值：⽅差：等于协⽅差：等于所以有结论：（2）初始条件未知：则其通解为：{y(t)}平稳的条件为：1 |a1|<12 且齐次解A(a1)^t为0：序列从很久前开始（即t很⼤，且结合1，则为0），或该过程始终平稳（A=0）所以说，解的稳定性和序列的平稳性是不⼀样的。

这两条对所有的ARMA(p,q)模型都适⽤。

（对于任意的ARMA(p,q)模型，齐次解为0是平稳性必要条件）（ARMA(p,q)模型的齐次解为或）6对于ARMA(2,1)模型的平稳性：模型表达式为：（2.16）（截距项不影响平稳性，略去）设其挑战解为：（⽤待定系数法）则系数应当满⾜⽅程：（2.17）序列{阿尔法i}收敛的条件是⽅程（2.16）对于的齐次⽅程的特征根都在单位圆之内（因为2.17中的差分⽅程对于的特征⽅程和⽅程2.16对于的特征⽅程是⼀模⼀样的）我们之所以只考虑特解，是因为我们让齐次解为0.此时该挑战解/特解：均值为：⽅差为：（t很⼤时⽤级数求和）协⽅差为：等于所以其平稳性条件为（t很⼤）：1模型对应的齐次⽅程的特征⽅程的特征根在单位圆内2齐次解为0。

平稳时间序列的统计特征
时间序列是统计学中最重要的概念之
一，它描述了一段时间内变量随时间变化的情况。

平稳时间序列是指变量的均值、方差和自相关系数不随时间变化的时间序列。

平稳时间序列的统计特征是非常重要的，可以帮助我们理解变量的变化特性，并且可以用来对未来变量的变化做出预测。

首先，要确定一个时间序列是否是平稳的，可以使用单位根检验（Unit Root Test）。

如果检验结果表明变量是平稳的，就可以进一步分析它的统计特征。

其次，要了解一个平稳时间序列的统计特征，我们首先要研究它的均值和方差。

均值是描述一个变量的中心位置的指标，而方差是描述变量变化的程度的指标。

如果均值和方差不变，那么这个时间序列就是平稳的。

另外，我们还要研究平稳时间序列的自相关系数。

自相关系数可以衡量相邻变量之间的相关性，它可以用来判断一个时间序列是否是平稳的。

如果这个时间序列的自相关系数是恒定的，那么这个时间序列就是平稳的。

37.时间序列分析I —平稳性及纯随机性检验(_)基本概念一、什么是时间序列？为了研究某一事件的规律，依据时间发生的顺序将事件在多个时刻的数值记录下来，就构成了一个时间序列。

对时间序列进行观察、研究，找寻它变化发展的规律，预测它将来的发展趋势就是时间序列分析。

例如，国家或地区的年度财政收入，股票市场的每日波动，气象变化，工厂按小时观测的产量等等。

注：随温度、高度等变化而变化的离散序列，也可以看作时间序列。

二、时间序列的特点(1)顺序性；(2)随机性；(3)前后时刻(不一定相邻)的依存性；(4)整体呈趋势性和周期性。

三、时间序列的分类按研究对象的数目：一元时间序列、多元时间序列；按序列统计特性：平稳时间序列、非平稳时间序列；按分布规律：高斯时间序列、非高斯时间序列。

四、研究方法1.平稳时间序列分析；2.非平稳时间序列分析（确定性分析、随机性分析）。

五、其它任何时间序列经过合理的函数变换后都可以被认为是由下列三部分叠加而成：（1）趋势项部分；（2）周期项部分；（3）随机项部分（随机信号、随机噪声）例如，手机销售的月记录按年增长（趋势项）；按季节周期波动（周期项）；随机信号和随机噪声。

时间序列分析的主要任务就是：上面三部分分解岀来，是研究平稳随机过程的变化规律，建立特定的ARIMA模型（要求大体平稳、可能含有周期但不能有规则性的线性指数等类型趋势项）。

六、方法性工具1.差分运算(1)k步差分间隔k期的观察值之差：Ak=X r Xr-jt(2)p阶差分/^t=xr xt.i称为一阶差分；P△"兀称为p 阶差分；/=0SAS函数实现：diffw(x)2.延迟算子延迟算子作用于时间序列，时间刻度减小1个单位(序列左移一位): Bx t=x t.\, ...... , Wxt^Xt-p.SAS函数实现:lagn(x)用延迟算子表示k步差分和p阶差分为：A k=xr^4=(l-B k)x r/=0(二)平稳时间序列一-概念平稳时间序列按限制条件的严格程度，分为严平稳时间序列：序列所有的统计性质都不会随着时间的推移而发生变化;宽平稳时间序列：序列的主要性质近似稳定，即统计性质只要保证序列的二阶矩平稳，即对任意的时间匚S,匕序列X,满足：EX； <4EX=/八tEg - “J（Xs - 心=Eg-“Q（兀+H -“卄）二、平稳时间序列的统计性质（1）均值为常数；（2）自协方差只依赖于时间跨度；若定义自协方差函数为Y（f,s） = E（X,-//；）（Xs 屮）则可由二元函数简化为一元函数y（r-5）,得延迟k自协方差函Y 伙）=Y（M+Q由此易知平稳时间序列必具有常数方差:D(Xt)= E(X申)2=y(r,r)= 丫(0)时间序列自相关函数:Eg -“)(X$ -儿)冋• DXs延迟k自相关函数:门⑴=E（X厂丛）（x屮—耳j二y（k） = 型一J DX’DX^ ~ "（0）7（0）— /（°）基木性质：（I ） P （O ）=1；(2) p(-k)= p(k);(3) 自相关阵为对称负定阵；(4) 非唯一性。

第二章 平稳时间序列模型本章将介绍Box-Jenkins 方法，主要包括一元平稳时间序列的识别、估计、诊断和预测方法。

2．1 平稳性时间序列t y 的均值和协方差 ()t t E y μ=,cov(,)[()()]t s t t s s t s y y E y y μμγ=--=一个随机过程的线性性质可由均值和协方差来描述。

如果这个过程是正态过程， ,,t t s μγ可以完全刻画这个随机过程的分布性质。

如果没有正态性质，但生成过程是线性的，则在它的均值和方差中可获得关于这个过程的更多的重要特征。

下面的问题是如何来估计t μ，对于一些过程我们可以得到大量的实现（反复做观测）,1,2,,.1,2,,.jt y t n j k ==那么，t μ的估计是11ˆkt jt j y k μ==∑但对大多数过程来说，得不到更多的实现。

如，不可能把经济停下来，然后重新开始观测。

对一个实现，不可能估计出t μ。

为了克服这个困难，时间序列分析要做如下的假设：均值和方差不随时间而改变。

如果对任何t, t-s, 都有μ==-)()(s t t y E y E222)()(y s t t y E y E σμμ=-=--s s j t j t s t t y y y y γ==----),cov(),cov(这里 2,y μσ都是常量，与时间无关，s γ是依赖于s 的常量。

这样的随机过程称为协方差平稳。

可以简单地说，如果一个时间序列的均值和协方差不受时间变化影响，则称这个时间序列是协方差平稳。

在一些文献中，协方差平稳的过程也称为弱平稳，二阶矩平稳或宽平稳过程。

（注意一个强平稳过程不一定有有限的均值和方差）。

一个更进一步的假设是遍历性（ergodic ）。

这是一个较难理解的一个概念。

遍历性是指，按时间平均11nn t t y y n ==∑是总体均值μ的无偏、一致估计。

即(),()0,()n n E y Var y n μ=↓→∞。