第03章 空间问题有限元法
- 格式:pdf
- 大小:295.05 KB
- 文档页数:5




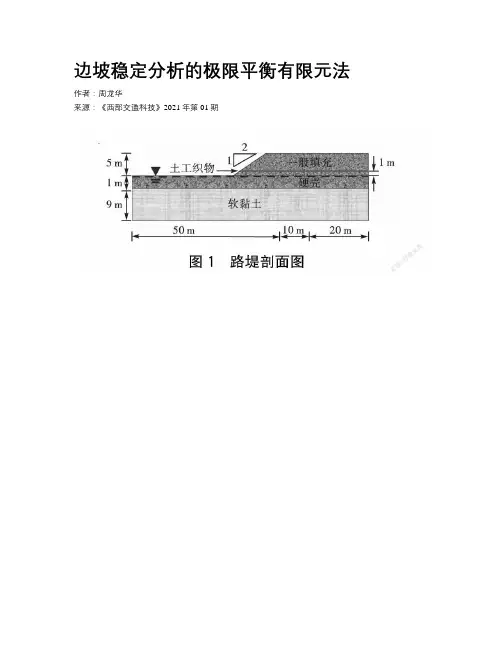
边坡稳定分析的极限平衡有限元法作者:***来源:《西部交通科技》2021年第01期摘要:极限平衡软件SLOPE/W和有限元程序PLAXE是目前岩土工程中常用的两种软件程序。
采用极限平衡法进行边坡分析时,需要将地面划分为若干垂直层面,并使用静态平衡方程计算各层面的安全系数(FOS)和应力,而有限元法则需要输入土的性质和单元的弹塑性参数。
文章比较了有限元法和极限平衡法在边坡稳定性分析中的应用,讨论了各种方法的适用性和局限性,并评估了边坡稳定性分析模型输出的实用性,可为边坡稳定性评估提供可靠依据。
关键词:有限元法;极限平衡;边坡稳定性中图分类号:U416.1+4文献标识码:ADOI:10.13282/ki.wccst.2021.01.022文章編号:1673-4874(2021)01-0078-030引言随着对基础设施和自然资源需求的不断扩大,对工程开挖和道路建设的要求也越来越高。
在工程建设过程中,山体滑坡和地震等自然灾害是岩土工程师和地质学家面临的重要问题。
边坡的稳定性是施工前、施工中、施工后各利益相关者共同关心的重要问题,如果要改变边坡稳定技术,安全系数(FOS)的微小差异可能导致施工成本的巨大差异。
这一点很重要,因为目前还没有明确的证据表明,哪种方法能产生最可接受的结果[1-3]。
与基础设施有关的土质边坡失稳是一个持续存在的问题,因为边坡破坏危及公共安全并导致昂贵的修复工作。
近几十年来,人们开发了一系列功能强大的边坡稳定分析设计软件包。
这些程序包括边坡稳定分析的极限平衡法和有限元法。
极限平衡法有许多局限性和不一致性,但被认为是最常用的方法。
随着技术进步,有限元程序简化了边坡稳定性分析。
SLOPE/W和PLAXIS是目前岩土工程师使用的两种常用软件程序。
SLOPE/W和PLAXIS分别用于极限平衡法和有限元法,每一个程序都被用来确定边坡的安全系数及其随后的设计要求。
根据所需的信息,分析和比较每个程序的结果将有助于确定哪个程序更准确。



第三部分非线性分析第一章非线性有限元概述1.1非线性行为1、 非线性结构的基本特征是结构刚度随载荷的改变而变化。
如果绘制一个非线 性结构的载荷一位移曲线,则 力与位移的关系是非线性函数。
2、 引起结构非线性的原因:a 几何非线性:大应变,大位移,大旋转 (例如钓鱼竿的变形)b 材料非线性:塑性,超弹性,粘弹性,蠕变c 状态改变非线性:接触,单元死活3、 非线性行为一一分析方法特点A 不能使用叠加原理!B 结构响应与路径有关,也就是说加载的顺序可能是重要的。
C 结构响应与施加的载荷可能不成比例。
1.2非线性分析的应用1、 一些典型的非线性分析的应用包括: 非线性屈曲失稳分析金属成形研究碰撞与冲击分析制造过程分析(装配、部件接触等)材料非线性分析 (塑性材料、聚合物)2、 橡胶底密封:一个包含几何非线性(大应变与大变形),材料非线性(橡胶), 及状态非线性(接触)的例子。
2.1非线性方程组的解法1、求解一个结构的平衡问题通常等于求解结构的总位能的驻值 问题。
结构总位能n : 口 "3弋门心 2、 增量法:就是将荷载分成一系列的荷载增量,即 ANSYS 中的荷载步或荷载子 步。
A 要点:在每一个荷载增量求解完成后,继续进行下一个荷载增量之前, 刚度矩阵以反映结构刚度的变化。
B 增量法的优点:可以追踪结构变形历程,这对于材料或几何非线性(特别是 极限值屈曲分析)十分有用。
C 增量法的缺点:随着荷载步增量的增加而产生积累误差,导致荷载-位移曲 线飘移。
D 对飘移进行平衡修正,可以大大提高增量法的精度。
应用最广的就是在每一 级载荷增量上用Newton-Raphsor 或其变形的迭代法。
3、 迭代法:割线刚度法:收敛性差,因此很少应用切线刚度法Newto n-Ra phsor 迭代法:切向刚度法中 2.2 Newto n-Ra phsor 迭代法 1、 优点:对于一致的切向刚度矩阵有 二次收敛速度。



5288|中国组织工程研究|第25卷|第33期|2021年11月三维有限元法分析腰椎不同尺寸关节突成形后相关节段的生物力学特征余 洋1,谢一舟1,石 银1,吴卫东2,顾党伟1,樊效鸿1文题释义:腰椎经皮内镜:与脊柱内窥镜类似,是一个配备有灯光的管子,它从患者身体侧方或者侧后方(可以平可以斜的方式)进入椎间孔,在安全工作三角区实施手术或通过患者后方从椎板间隙进行手术。
在椎间盘纤维环之外操作,在内窥镜直视下可以清楚看到突出的髓核、神经根、硬膜囊和增生的骨组织,然后使用各类抓钳摘除突出组织、镜下去除骨质、射频电极修复破损纤维环。
腰椎经皮内镜手术是同类手术中对患者创伤最小、效果最好的椎间盘突出微创疗法。
三维有限元:利用数学近似的方法对真实物理系统(几何和载荷工况)进行模拟,利用简单而又相互作用的元素(即单元),就可以用有限数量的未知量去逼近无限未知量的真实系统。
摘要背景:腰椎经皮内镜在全国乃至全世界范围内开展的如火如荼,经椎间孔的侧入路是目前腰椎经皮内镜技术最常用的入路之一,但是对于其术后造成相关节段的生物力学影响鲜有报道。
目的:通过三维有限元法模拟对比不同尺寸(7.5,10,15 mm)的关节突成形并探究其对腰椎相关节段生物力学的影响。
方法:建立L 3-L 5三维有限元模型并验证其有效性。
模拟L 4/5腰椎经皮内镜手术中的关节突成形术,以临床上穿刺针与水平面及冠状面的夹角,以L 5上关节突基底部作为穿刺靶点,根据穿刺路径分别做直径为7.5,10,15 mm 的环锯环切成形,从而获得L 5上关节突基底部不同直径成形的三维有限元模型。
通过对正常模型、7.5,10,15 mm 直径成形有限元模型在6个方向上施加载荷,计算各模型在前屈、后伸、左屈、右屈、左旋、右旋6种状态下操作节段(L 4/5)及邻近节段(L 3/4)椎间盘Von Mises 应力极值和相关节段的活动度情况,并进行相关对比研究,以明确不同尺寸的关节突成形对腰椎生物力学稳定性的影响。