下载文档原格式
有限空间布置重点工作总结
在现代社会，我们常常面临有限的空间，需要将重点工作进行合理布置。
在这
篇文章中，我们将探讨如何在有限的空间内有效地布置重点工作，以提高工作效率和生产力。
首先，要对重点工作进行明确的界定。
在有限的空间内，我们不可能同时进行
所有的工作，因此需要确定哪些工作是最重要的，最需要优先处理的。
这样可以确保我们在有限的空间内集中精力进行最重要的工作，提高工作效率。
其次，要充分利用空间资源。
在有限的空间内，我们需要充分利用各种资源，
包括桌面空间、文件柜、墙壁等，将工作进行合理布置。
可以使用文件夹、文件盒等工具，将文件整理归档，避免杂乱无章，提高工作效率。
另外，要合理安排工作时间。
在有限的空间内，我们需要合理安排工作时间，
将重点工作集中在最有效的时间段内进行。
这样可以确保我们在有限的空间内充分发挥工作效率，提高生产力。
最后，要保持空间整洁。
在有限的空间内，保持整洁是非常重要的。
整洁的工
作环境可以提高工作效率，减少工作中的混乱和压力，使我们更加专注于重点工作。
总之，在有限的空间内布置重点工作需要我们明确工作重点、充分利用空间资源、合理安排工作时间和保持空间整洁。
只有这样，我们才能在有限的空间内提高工作效率，提高生产力。
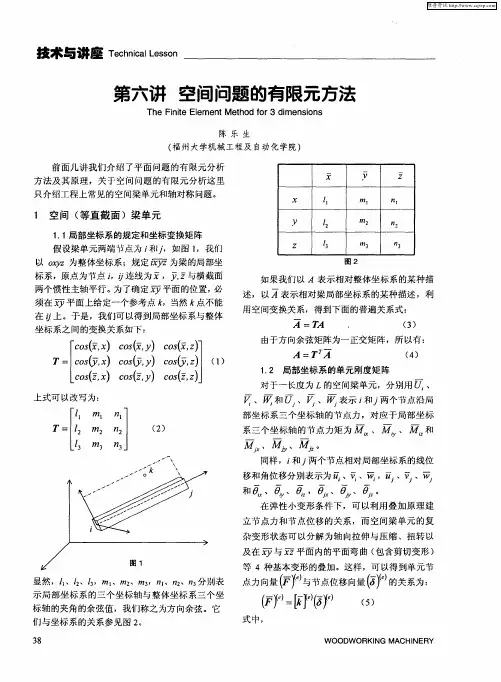
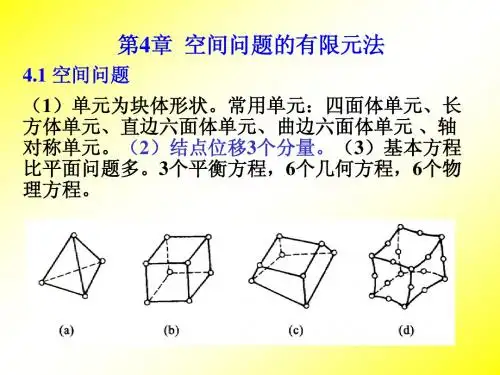
第三章 空间问题的有限元方法引言许多工程实际问题，属于空间问题，由于结构形状或受力的复杂性，用经典弹性理论去求解它们的解析解是不可能的。
而有限元法处理此类问题， 原则上不存在什么困难，本章将介绍一般空间问题的四面体单元。
一般空间问题的有限元列式3.2.1 单元位移模式及插值函数空间问题中，每个单元有四个结点，编码为i,j,m,p。
每个结点有3 个位移分量。
每个结点的位移可用位移矢量i 表示，即u iiv i(i , j ,m, p)w i单元结点的位移向量可表示为ieju i v iw i u j v j w ju m v m w m u pv pw pTmpe为单元结点位移列阵。
假设单元内的位移模式选取一次多项式u 1 2x3y4zv56 x7 y8 z（3.2.1 ）w910x11y12z由于四个结点也在单元内，满足位移模式，于是得u i 12xi 3yi 4ziu j 1 2xj 3yj 4zj（ 3.2.2 ）u m12 xm 3 ym4 zmu p12xp 3yp 4zp上式是关于1 ,2, 3,4 的线性方程组。
1, 2 , 3, 4 是待定常数，也称为广义坐标。
它可由（ 3.2.2 ）式求出。
上式的系数行列式是1x i y i z i1x j y j z j2V（3.2.3 ）Dx m y m z m11x p y p z p上式中当 i,j,m,p 的编号顺序满足右手法则， V值为正，其大小为四面体体积，因此为了方便单元的编号一般满足右手法则。
求得1 , 2 , 3 , 4后,回代入位移模式得u N i u i N j u j N m u m N p u p(3.2.4)式中N i1(a i b i x c i y d i z)(i , j, m, p) (3.2.5) 6Vx j y j z ja i x m y m z mx p y p z p1y j z jb i1y m z m1y p z p1x j z jc i 1x m z m(i , j , m, p) （3.2.6）1x p z p1x j y jd i1x m y m1x p y p上式下标 (i ,j , m, p) 轮换，可得 a j , b j ,c j , d j, a m ,b m ,c m , d m及 a p , b p , c p ,d p。
同理 , 也可得到其它两式 , 于是得u N i u i N j u j N m u m N p u pv N i v i N j v j N m v m N p v p（ 3.2.7）w N i w i N j w j N m w m N p w p 其中N i1(a i b i x c i y d i z)(i , j, m, p) (3.2.8) 6VN i , N j , N m , N p称为单元的插值函数或形函数，这里它是x, y, z的一次函数，其中a i ,b i , c i ,d i， a j , b j , c j , d j, a m ,b m , c m , d m及 a p , b p , c p ,d p是常数，由表达式可知，它完全由单元的大小和方位确定，一旦单元确定了，这些常数也完全确定。
（ 3.2.7 ）式的矩阵形式是u N i00N j00N m00N p0i 0u v0N i00N j00N m00N pj 0w00N i00N j00N m00m N ppiIN i IN j IN m IN p jmp[ N ] i[ N ] j[ N ] m[ N ] p e N e（3.2.9 ）N称为插值函数矩阵或形函数矩阵。
3.2.2 ．应变矩阵和应力矩阵⑴应变确定了单元位移后，可以很方便地利用几何方程和物理方程求得单元的应变和应力。
在（ 1.4.21 ）式的几何方程中，位移用（）式代入，得到单元应变为x y z xy yz zxuxvywzu v y x v w z y w u x z[ B] i[ B] j[ B] m[ B] p e B e（3.2.10 ）B称为应变矩阵。
应变矩阵的分块矩阵 [ B]i是b i000c i0100 d i(i , j , m, p)（3.2.11 ）[ B] ic i b i06V0d i c id i0b i可以看出，应变矩阵 B 中的元素都是常量，从而单元中的应变都是常量，所以三维线性位移模式的四面体单元是常应变单元。
⑵ 应力单元应力可以根据物理方程求得，其应力应变关系如下：x 1 [x( Ey1 [y( Ez1 [z(Eyz yz /zx zx/xy xy /y z )]z x )]x y )]或Ex ,Ex12yz yz12(1)Ey ,Ey12zx zx12(1)Ez ,Ez12xy xy12(1)于是应力向量可表示为D DB e S e（3.2.12 ）式中 D 为弹性矩阵，而111111E(1)1111 2D2)00(1 )(12(1)00120 2(1)12 0)2(1（3.2.13 ）从而可以到，三大物理参量，都可以用单元结点位移向量表示：u N eTB ex y z xy yz zxTe S ex y z xy yz zx DB由于 N，B，S 都是已知的矩阵，只要求得 e ，则单元内的位移、应变和应力就可以就得，问题是：如何求结点位移向量3．单元刚度矩阵和结点载荷向量对于三维单元，单元刚度矩阵也具有上章所讨论的单元刚度矩阵的一般形式，即KeV e B TDBtdxdyB TDBV（ 3.2.15 ）写成分块矩阵的形式K ii e K ij e K im e K ip eK eK e jiK jj e K e jm K e jp（3.2.16 ）K mi eK mjeK mmeK mp eK pi e K pj e K pm e K pp e每个子矩阵为K rs e [ B r ] T D[ B s ]V等效结点载荷P f eN T fdVV eP S eeN T TdSSP e P f e P S e（3.2.17 ）P e 是单元等效结点载荷（体力和面力引起的等效结点力） ， F e 是其他单元对该单元的作用力，则单元结点力为P e 与 F e 和。
体积力的等效结点载荷：P if ef xP f eP jf e VeN T f y dxdydzP mf ef zP ix ef xP if eP iy eV eNif y dxdydz (i, j , m, p)P iz e ff z面积力的等效结点载荷：P S eeN T TdSSPeTixP S eP jeSeN TT y dSP m eT zSP ix e T xP iS eP iy e N i T y dSP iz eST zS这里给出两种常见的载荷的等效结点力：ⅰ）均质单元的自重分配到四个结点的等效结点力，其数值都等于 gV / 4 ；ⅱ）设单元的某一边界面上，例如ijm ，受有线性分布载荷，它在i, j , m 三个结点处的强度分别为 q i , q j , q m ，则分配到结点 i 上的等效结点力的数值为P i e1 q i1q j1q m A ijm(i , j, m)62 2A ijm 为受力面三角形面积。
方向与原方向平行。
3.2.4 ．结构刚度矩阵和结构载荷列阵的集成由单元分析可得有限元列式为K eeP e F e（ 3.2.18 ）经叠加，组合，得有限元方程KP其中N eKK ee 1N EPP ee 1式中K e 为扩大后的单元刚度矩阵；P e 为扩大后的单元等效结点载荷；N e 为结构系统的单元数。
