轴对称图形证明

专题十：与翻折或轴对称作图有关的几何证明题解析专题导例如图，M、N是正方形ABCD的边CD上的两个动点，满足AM＝BN，连接AC交BN于点E，连接DE交AM于点F，连接CF，若正方形的边长为6，则线段CF的最小值是．【分析】：先判断出Rt△ADM≌Rt△BCN（HL），得出∠DAM＝∠CBN，进而判断出△DCE≌△BCE （SAS），得出∠CDE＝∠CBE，即可判断出∠AFD＝90°，根据直角三角形斜边上的中线等于斜边的一半可得OF＝AD＝3，利用勾股定理列式求出OC，然后根据三角形的三边关系可知当O、F、C 三点共线时，CF的长度最小．方法剖析轴对称的性质（1）对应线段相等，对应角相等；对称点的连线被对称轴垂直平分；（2）轴对称图形变换的特征是不改变图形的形状和大小，只改变图形的位置，新旧图形具有对称性；（3）轴对称的两个图形，它们对应线段或延长线相交，交点在对称轴上.轴对称（折叠）的思考层次全等变换：对应边相等，对应角相等；对称轴性质：对应点所连线段被对称轴（折痕）垂直平分，对称轴（折痕）上的点到对应点的距离相等；指出：（1）在翻折下，前后的图形关于折痕成轴对称，注意前后的图形成镜面对称，即前后的图形的左右位置互换；（2）翻折或对称中建构勾股方程来求取线段长及对最值类问题进行探究；（3）轴对称常见的结构，折叠会产生垂直平分，等腰三形.导例答案：解：如图，在正方形ABC D中，AD＝BC＝CD，∠ADC＝∠BCD，∠DCE＝∠BCE，在Rt△ADM和Rt△BCN中，，∴Rt△ADM≌Rt△BCN（HL），∴∠DAM＝∠CBN，在△DCE和△BCE中，，∴△DCE≌△BCE（SAS），∴∠CDE＝∠CBE∴∠DAM＝∠CDE，∵∠ADF+∠CDE＝∠ADC＝90°，∴∠DAM+∠ADF＝90°，∴∠AFD＝180°﹣90°＝90°，取AD的中点O，连接OF、OC，则OF＝DO ＝AD＝3，在Rt△OD C中，OC ＝＝3根据三角形的三边关系，OF+CF＞OC，∴当O、F、C三点共线时，CF的长度最小，最小值＝OC﹣OF＝3﹣3．故答案为：3﹣3．典型例题类型一：利用已知直线作对称图形进行证明例1、在等边△AB C中，点D在BC边上，点E在AC的延长线上，DE＝DA（如图1）．（1）求证：∠BAD＝∠EDC；（2）点E关于直线BC的对称点为M，连接DM，AM．①依题意将图2补全；②证明：在点D运动的过程中，始终有DA＝AM．【分析】（1）先判断出∠BAD+∠CAD＝60°，进而得出∠BAD+∠E＝60°，即可得出结论；（2）①由对称性即可补全图形；②由对称性判断出DM＝DE，∠MDC＝∠EDC，再用三角形的外角的性质，判断出∠ADC＝∠B+∠BAD＝∠B+∠MDC，进而判断出△ADM是等边三角形，即可得出结论．类型二：对已知图形进行翻折进行证明例2．如图，矩形ABC D中，AB＝4，AD＝3，把矩形沿直线AC折叠，使点B落在点E处，AE交CD于点F，连接DE．（1）求证：△DEC≌△EDA；（2）求DF的值；（3）在线段AB上找一点P，连结FP使FP⊥AC，连结PC，试判定四边形APCF的形状，并说明理由，直接写出此时线段PF的大小．【分析】（1）根据矩形的性质、轴对称的性质可得到AD＝EC，AE＝DC，即可证到△DEC≌△EDA （SSS）；（2）易证AF＝CF，设DF＝x，则有AF＝4﹣x，然后在Rt△ADF中运用勾股定理就可求出DF的长．（3）根据三角形的内角和定理求得∠APF＝∠AFP根据等角对等边得出AF＝AP进而得出FC＝AP，从而证得四边形APCF是平行四边形，又因为FP⊥AC证得四边形APCF为菱形，然后根据菱形的面积S菱形＝PF•AC＝AP•AD，即可求得．专项突破1.如图，在Rt△AB C中，∠C＝90°，点D、E分别是BC、AB上一个动点，连接DE．将点B沿直线DE折叠，点B的对应点为F，若AC＝3，BC＝4，当点F落在AC的三等分点上时，BD的长为．2．如图，正方形ABC D中，点E是BC延长线上一点，连接DE，过点B作BF⊥DE于点F，连接F C．（1）求证：∠FBC＝∠CDF；（2）作点C关于直线DE的对称点G，连接CG，FG，猜想线段DF，BF，CG之间的数量关系，并证明你的结论．3.已知矩形ABCD，其中AD＞AB，依题意先画出图形，然后解答问题．（1）F为DC边上一点，把△ADF沿AF折叠，使点D恰好落在BC上的点E处．在图1中先画出点E，再画出点F，若AB＝8，AD＝10，直接写出EF的长为；（2）把△ADC沿对角线AC折叠，点D落在点E处，在图2先画出点E，AE交CB于点F，连接BE．求证：△BEF是等腰三角形．4.如图，Rt△AB C中，∠ACB=90°，AC=BC，点D为AB边上的一个动点（不与点A，B及A B中点重合），连接CD，点A关于直线CD的对称点为点E，直线BE，CD交于点F．（1）如图1，当∠ACD=15°时，根据题意将图形补充完整，并直接写出∠BFC的度数；（2）如图2，当45°＜∠ACD＜90°时，用等式表示线段AC，EF，BF之间的数量关系，并加以证明．5．在Rt△AB C中，∠ACB＝90°，CA＝C B．点D为线段BC上一个动点（点D不与点B，C重合），连接AD，点E在射线AB上，连接DE，使得DE＝D A．作点E关于直线BC的对称点F，连接BF，DF．（1）依题意补全图形；（2）求证：∠CAD＝∠BDF；（3）用等式表示线段AB，BD，BF之间的数量关系，并证明．6．如图①，在等腰三角形AB C中，AB＝AC＝8，BC＝14．如图②，在底边BC上取一点D，连结AD，使得∠DAC＝∠AC D．如图③，将△ACD沿着AD所在直线折叠，使得点C落在点E处，连结BE，得到四边形ABE D．则BE的长是．7．在等边三角形ABC外侧作射线AP，∠BAP=α，点B关于射线AP的对称点为点D，连接CD交AP于点E.（1）依据题意补全图形；（2）当α=20°时，∠ADC= ；∠AEC= ；（3）连接BE，求证：∠AEC=∠BEC；（4）当0°<α<60°时，用等式表示线段AE，CD，DE之间的数量关系，并证明．8.在等边△ABC外侧作直线AP，点B关于直线AP的对称点为D，连结BD，CD，其中CD交直线AP与点E．（1）如图1，若∠P AB＝30°，则∠ACE＝；（2）如图2，若60°＜∠P AB＜120°，请补全图形，判断由线段AB，CE，ED可以构成一个含有多少度角的三角形，并说明理由．9．如图1，将一张矩形纸片ABCD沿着对角线BD向上折叠，顶点C落到点E处，BE交AD于点F.(1)求证：△BDF是等腰三角形；(2)如图2，过点D作DG∥BE，交BC于点G，连结FG交BD于点O.①判断四边形BFDG的形状，并说明理由；②若AB＝6，AD＝8，求FG的长．10.【问题情境】如图①，在Rt△AB C中，∠ACB＝90°，AC＝BC，点D为A B中点，连结CD，点E为CB上一点，过点E且垂直于DE的直线交AC于点F．易知：BE＝CF．（不需要证明）【探索发现】如图②，在Rt△AB C中，∠ACB＝90°，AC＝BC，点D为A B中点，连结CD，点E为CB的延长线上一点，过点E且垂直于DE的直线交AC的延长线于点F．【问题情境】中的结论还成立吗？请说明理由．【类比迁移】如图③，在等边△AB C中，AB＝4，点D是A B中点，点E是射线AC上一点（不与点A、C重合），将射线DE绕点D逆时针旋转60°交BC于点F．当CF＝2CE时，CE＝．11．在△AB C中，∠ACB＝90°，AC＜BC，点D在AC的延长线上，点E在BC边上，且BE＝AD，（1）如图1，连接AE，DE，当∠AEB＝110°时，求∠DAE的度数；（2）在图2中，点D是AC延长线上的一个动点，点E在BC边上（不与点C重合），且BE＝AD，连接AE，DE，将线段AE绕点E顺时针旋转90°得到线段EF，连接BF，DE．①依题意补全图形；②求证：BF＝DE．专题十：与翻折或轴对称作图有关的几何证明题解析例1．解：（1）∵△ABC是等边三角形，∴∠BAC＝∠ACB＝60°，∴∠BAD+∠CAD＝60°，∵DE＝DA，∴∠CAD＝∠E，∴∠BAD+∠E＝60°，∵∠EDC+∠E＝∠ACB＝60°，∴∠BAD＝∠EDC；（2）①补全图形如图2所示；②∵△ABC是等边三角形，∴∠B＝60°，由对称性得，∠EDC＝∠MDC，由（1）知，∠EDC＝∠BAD，∴∠MDC＝∠BAD，∵∠ADC＝∠B+∠BAD＝∠B+∠MD C．∴∠ADM＝∠B＝60°，由对称性得，DM＝DE，∵DE＝DA，∴DA＝DM，∴△ADM是等边三角形，∴DA＝DM，即：在点D运动的过程中，始终有DA＝AM．例2．（1）证明：∵四边形ABCD是矩形，∴AD＝BC，AB＝CD，AB∥CD，∴∠ACD＝∠CAB，∵△AEC由△ABC翻折得到，∴AB＝AE，BC＝EC，∠CAE＝∠CAB，∴AD＝CE，DC＝EA，∠ACD＝∠CAE，在△ADE与△CE D中，，∴△DEC≌△EDA（SSS）；（2）解：如图1，∵∠ACD＝∠CAE，∴AF＝CF，设DF＝x，则AF＝CF＝4﹣x，在RT△ADF中，AD2+DF2＝AF2，即32+x2＝（4﹣x）2，解得；x＝，即DF＝．（3）解：四边形APCF为菱形，设AC、FP相较于点O∵FP⊥AC∴∠AOF＝∠AOP又∵∠CAE＝∠CAB，∴∠APF＝∠AFP∴AF＝AP∴FC＝AP又∵AB∥CD∴四边形APCF是平行四边形又∵FP⊥AC∴四边形APCF为菱形，在矩形ABC D中，AB＝4，AD＝3，∴AC＝5，∵S菱形＝PF•AC＝AP•AD，∵AP＝AF＝4﹣＝∴PF＝＝．专项突破1.解：∵折叠∴BD＝DF，∵点F落在AC的三等分点上∴CF＝1或CF＝2，若CF＝1时，在Rt△CDF中，DF2＝CD2+CF2，∴BD2＝（4﹣BD）2+1∴BD＝当CF＝2时，在Rt△CDF中，DF2＝CD2+CF2，∴BD2＝（4﹣BD）2+4∴BD＝故答案为：或2．解：（1）∵ABCD为正方形，∴∠DCE＝90°．∴∠CDF+∠E＝90°，又∵BF⊥DE，∴∠FBC+∠E＝90°，∴∠FBC＝∠CDF（2）如图所示：在线段FB上截取FM，使得FM＝F D．∵∠BDC＝∠MDF＝45°，∴∠BDM＝∠CDF，∵＝＝，∴△BDM∽△CDF，∴＝＝，∠DBM＝∠DCF，∴BM＝CF，∴∠CFE＝∠FCD+∠CDF＝∠DBM+∠BDM＝∠DMF＝45°，∴∠EFG＝∠EFC＝45°，∴∠CFG＝90°，∵CF＝FG，∴CG＝CF，∴BM＝CG，∴BF＝BM+FM＝CG+DF．补充方法：连接GM，证明四边形BMGC是平行四边形即可．3.解：（1）如图1，在BC上截取AE＝AD得点E，作AF垂直DE交CD于点F（或作∠AED的平分线AF交CD于点F，或作EF垂直AE交CD于点F等等），∵四边形ABCD是矩形，∴AB＝CD＝8，AD＝BC＝10，∠B＝∠C＝90°，在Rt△ABE中，BE＝＝6，∴EC＝10﹣6＝4，设EF＝DF＝x，在Rt△EF C中，则有x2＝（8﹣x）2+42，解得x＝5，∴EF＝5．故答案为：5；（2）证明：如图2，作DH垂直AC于点H，延长DH至点E，使HE＝DH．方法1：∵△ADC≌△AEC，∴AD＝AE＝BC，AB＝DC＝EC，在△ABE与△CE B中，，∴△ABE≌△CEB（SSS），∴∠AEB＝∠CBE，∴BF＝EF，∴△BEF是等腰三角形．方法2：∵△ADC≌△AEC，∴AD＝AE＝BC，∠DAC＝∠EAC，又∴AD∥BC，∴∠DAC＝∠ACB，∴∠EAC＝∠ACB，∴F A＝FC，∴FE＝FB，∴△BEF是等腰三角形．4.（1）如图1中，连接E C．∵A，E关于CD对称，∴∠DCA=∠DCE=15°，CA=CE=C B．∵∠ACB=90°，∴∠ECB=60°，∴△ECB是等边三角形，∴∠CEB=60°，∵∠CEB=∠BFC+∠DCE，∴∠BFC=60°-15°=45°．（2）结论：EF2+BF2=2AC2．理由：如图2，连接CE，AF，延长AC交FE的延长线于点G．∵A，E关于CD对称，∴AC=CE，AF=EF，又∵CF=CF，∴△ACF≌△ECF（SSS），∴∠CAF=∠1，∵AC=BC，∴BC=CE，∴∠1=∠2，∴∠CAF=∠2，∵∠ACB=90°，∴∠G+∠2=90°，∴∠CAF+∠G=90°，∴∠AFG=90°，在Rt△AF B中，AB2=AF2+BF2，在Rt△AB C中，AB2=AC2+BC2=2AC2，∴BF2+AF2=2AC2，∴BF2+EF2=2AC2．5．（1）如图所示：（2）∵∠ACB＝90°，CA＝CB，∴∠BAC＝∠CBA＝45°，∴∠CAD+∠DAB＝45°，∵DA＝DE，∴∠DAE＝∠DEB，∵∠DBA是△DBE的一个外角，∴∠EDB+∠DEB＝∠DBA＝45°，∴∠EDB＝∠CAD，∵点E关于直线BC的对称点F，∴∠EDB＝∠FDB，∴∠CAD＝∠FDB；（3）线段AB，BD，BF之间的数量关系是AB﹣BF=√2BD，证明：过点D作AC的平行线交AB于M点，∴∠C＝∠MDB＝90°，∠CAB＝∠DMB＝45°，∴∠DMB＝∠DBM，∴DM＝DB，∴MB=√2BD，∵点E关于直线BC的对称点F，∴DE＝DF，∵AD＝DE，∴AD＝DF，∵AC∥MD，∴∠CAD＝∠ADM，∵∠CAD＝∠FDB，∴∠ADM＝∠FDB，∴△ADM≌△FDB（SAS），∴AM＝BF，∴AB﹣BF＝AB﹣AM＝MB，又∵MB=√2BD，∴AB﹣BF=√2B D．6.解：∵AB＝AC，∴∠ABC＝∠C，∵∠DAC＝∠ACD，∴∠DAC＝∠ABC，∵∠C＝∠C，∴△CAD∽△CBA，∴＝，∴＝，∴CD＝，BD＝BC﹣CD＝，∵∠DAM＝∠DAC＝∠DBA，∠ADM＝∠ADB，∴△ADM∽△BDA，∴＝，即＝，∴DM＝，MB＝BD﹣DM＝，∵∠ABM＝∠C＝∠MED，∴A、B、E、D四点共圆，∴∠ADB＝∠BEM，∠EBM＝∠EAD＝∠ABD，∴△ABD∽△MBE，∴＝，∴BE ＝＝＝．故答案为：．7．（1）如图；EDP（2）40°；60 °；（3）证明：∵点B关于射线AP的对称点为点D，∴△BAE≌△DAE．∴∠BAE=∠DAE=α．∵AD=AB=AC，∴∠ADC=()1806022α︒-︒+=60°－α．∴∠AEC=60°．∵∠ACB=60°，∠ACD=∠ADC=60°－α，∴∠BCE=α．∵∠ABC=60°，∠ABE=∠ADC=60°－α，∴∠BEC=60°．（4）证明：法一：在CD上截取AF=AE．F EDAB C P∵∠AEF =60°，∴△AEF 是等边三角形．∴∠AFC =∠AED =120°．∵∠ACD =∠ADC =60°－α，∴△ADE ≌△ACF ．∴DE =CF ．∴CD =2DE +EF ．∵AE =EF ，∴CD =2DE +AE ．法二：在CD 上截取BG =BE ．GEDAB C P∵∠BEC =60°，∴△BEG 是等边三角形．∴∠BGC =∠AED =120°．∵∠BCE =∠DAE =α，∴△BCG ≌△DAE ．∴AE =CG ．∵EG =BE =DE ，∴CD =2DE +CG ．∴CD =2DE +AE ．8.解：（1）连接AD ，如图1．∵点D 与点B 关于直线AP 对称，∴AD ＝AB ，∠DAP ＝∠BAP ＝30°，∵AB ＝AC ，∠BAC ＝60°，∴AD ＝AC ，∠DAC ＝120°，∴2∠ACE +60°+60°＝180°，∴∠ACE ＝30°，故答案为：30°；（3）线段AB ，CE ，ED 可以构成一个含有60°角的三角形．证明：连接AD ，EB ，如图2．∵点D 与点B 关于直线AP 对称，∴AD ＝AB ，DE ＝BE ，∴∠EDA ＝∠EBA ，∵AB ＝AC ，AB ＝AD ，∴AD ＝AC ，∴∠ADE ＝∠ACE ，∴∠ABE ＝∠ACE ．设AC ，BE 交于点F ，又∵∠AFB ＝∠CFE ，∴∠BAC ＝∠BEC ＝60°，∴线段AB ，CE ，ED 可以构成一个含有60°角的三角形．9．(1)根据折叠，∠DBC ＝∠DBE ，又AD ∥BC ，∴∠DBC ＝∠ADB ，∴∠DBE ＝∠ADB ，∴DF ＝BF ，∴△BDF 是等腰三角形(2)①菱形，理由：∵四边形ABCD 是矩形，∴AD ∥BC ，∴FD ∥BG ，又∵FD ∥BG ，∴四边形BFDG 是平行四边形，∵DF ＝BF ，∴四边形BFDG 是菱形②∵AB ＝6，AD ＝8，∴BD ＝10.∴OB ＝12BD ＝5.设DF ＝BF ＝x ，∴AF ＝AD －DF ＝8－x .∴在Rt △ABF 中，AB 2＋AF 2＝BF 2，即62＋(8－x )2＝x 2，解得x ＝254，即BF ＝254，∴FO ＝BF 2－OB 2＝（254）2－52＝154，∴FG ＝2FO ＝152 10.解：【问题情境】证明：∵在Rt △AB C 中，∠ACB ＝90°，AC ＝BC ，点D 为A B 中点， ∴CD ⊥AB ，CD ＝BD ＝AD ＝AB ，∠BCD ＝∠B ＝45°，∴∠BDC ＝90°，∵∠EDF ＝90°，∴∠CDF＝∠BDE，在△BDE与△CDF中，，∴△BDE≌△CDF（ASA），∴BE＝CF；【探索发现】成立，理由：∵在Rt△AB C中，D为A B中点，∴CD＝BD，又∵AC＝BC，∴DC⊥AB，∴∠DBC＝∠DCB＝45°，∵DE⊥DF，∴∠EDF＝90°，∴∠EDB+∠BDF＝∠CDF+∠BDF＝90°，∴∠CDF＝∠BDE，∴∠ADF＝∠CDE，∴AF＝CE，∴CF＝BE；【类比迁移】∵△ABC是等边三角形，∴∠A＝∠B＝60°，∵∠FDE＝60°，∴∠BDF＝120°﹣∠ADE，∠AED＝120°﹣∠ADE，∴∠BDF＝∠AED，∴△ADE∽△BDF，∴，∵点D为A B中点，AB＝4，∴AD＝BD＝2，AC＝BC＝4，∵CF＝2CE，∴设CE＝x，则CF＝2x，当点E在线段AC上时，∴AE＝4﹣x，BF＝4﹣2x，∴＝，解得：x＝3﹣，x＝3+（不合题意，舍去），∴CE＝3﹣，如图④，当点E在AC的延长线上时，∵AE＝4+x，BF＝4﹣2x，∴＝，解得：x＝﹣1+，（负值舍去），∴CE＝﹣1+．综上所述，CE＝3﹣或﹣1+，故答案为：3﹣或﹣1+．11.解：（1）∵∠AEB＝110°，∠ACB＝90°，∴∠DAE＝∠AEB﹣∠ACB＝20°；（2）①补全图形，如图所示．②证明：由题意可知∠AEF＝90°，EF＝AE．∵∠ACB＝90°，∴∠AEC+∠BEF＝∠AEC+∠DAE＝90°．∴∠BEF＝∠DAE．∵在△EBF和△ADE中，，∴△EBF≌△ADE（SAS）．∴DE＝BF．。

轴对称、中心对称图形的性质及应用一、轴对称图形如果把一个图形沿着某一条直线对折过来，在直线两旁的部分能够完全重合，那么这个图形叫做轴对称图形，这条直线叫做对称轴，能够重合的点互为对称点．轴对称图形具有以下的性质：(1)轴对称图形的两部分是全等的；(2)对称轴是连结两个对称点的线段的垂直平分线．在几何证题、解题时，如果是轴对称图形，则经常要添设对称轴以便充分利用轴对称图形的性质．譬如，等腰三角形经常添设顶角平分线；矩形和等腰梯形问题经常添设对边中点连线和两底中点连线；正方形，菱形问题经常添设对角线等等．另外，如果遇到的图形不是轴对称图形，则常选择某直线为对称轴，补添为轴对称图形，或将轴一侧的图形通过翻折反射到另一侧，以实现条件的相对集中．例1 已知直线l外有一定点 P，试在l上求两点A、B，使AB＝m(定长)，且PA＋PB最短．分析当把P点沿l方向平移至C(如图1)，使PC＝m，那么问题就转化为在l上求一点B，使CB＋PB为最短．作法过P作PC∥l，使PC＝m，作P关于l的对称点P＇，连结CP＇交l于B．在l上作AB＝m，点A、B为所求之两点．证在l上另任取A＇B＇＝m，连PA、PA＇、PB＇，CB＇，A＇P＇，B＇P＇，则PA＇＝P＇A＇，PB＇＝P＇B＇，又PA＇B＇C 为平行四边形，∴CB＇＝PA＇．∵CB＇＋B＇P＇＞CP＇，∴ PA＇＋PB＇＞PA＋PB．例2 如图2，△ABC中，P为∠A外角平分线上一点，求证：PB＋PC＞AB＋AC．分析由于角平分线是角的对称轴，作AC关于AP的轴对称图形AD，连结DP、CP，则DP＝CP，BD＝AB＋AC．这样，把 AB＋AC、AC、PB、PC集中到△BDP中，从而由PB＋PD＞BD，可得PB＋PC＞AB＋AC．证 (略)说明通过变为轴对称图形后，起到相对集中条件的作用，又有将折线化直的作用(如AB＋AC化直为BD)．例3 等腰梯形的对角线互相垂直，且它的中位线等于m，求此梯形的高．解如图3．设等腰梯形AD∥BC，AB＝DC，对角线AC与BD相交于O，且AC⊥BD，中位线EF＝m．过AD、BC的中点M、N作直线，由等腰梯形ABCD关于直线MN成轴对称图形，∴O点在MN上，且OA＝OD，OB＝OC，AM＝DM，BN＝CN．又 AC⊥BD，故△AOD和△BOC均为等腰直角三角形．2OM＝AD，2ON＝BC．∵AD＋BC＝2EF＝2m，∴2OM＋2ON＝2m．∴OM＋ON＝m，即梯形高MN＝m．例4 凸四边形EFGH的四个顶点分别在边长为a的正方形ABCD的四条边上．证如图4，连结AA2，EE3．正方形ABCD和正方形A1BCD1关于BC对称；EFGH和E1FG1H1关于BC对称；A1BCD1和A2B1CD1关于 CD1对称；E1FG1H1和 E2F1G1H2关于CD1对称；A2B1CD1和A2B2C1D1关于A2D1对称，E2F1G1H2和E3F2G2H2关于A2D1对称．例5 如果一个四边形关于它的两组对边中点的两条连线成轴对称，则此四边形为矩形．已知如图22－5．四边形ABCD中，M、F、N、E分别为各边的中点，且MN、EF为它的对称轴．求证 ABCD是矩形．分析欲证ABCD是矩形，首先证明它是平行四边形，再证明它有一个直角即可．证∵四边形ABCD关于EF成轴对称，∴DC⊥EF，AB⊥EF，∴AB∥DC．同理AD∥BC．∴ABCD是平行四边形．∴DC＝AB．又∵DE＝DC/2，AF＝AB/2．∴DE AF，∴ADEF为平行四边形．∴AD∥EF，而DE⊥EF，∴DE⊥AD，∠D＝Rt∠．∴ABCD是矩形．二、中心对称图形如果把一个图形绕着某一点旋转180°后，能和原图形重合，那么这个图形叫做中心对称图形．这个点叫做对称中心，能重合的点互为对称点．中心对称图形具有以下性质：(1)关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分．(2)关于中心对称的两个图形，对应线段平行(或在同一条直线上)且相等．平行四边形是中心对称图形．矩形、菱形、正方形既是中心对称图形，也是轴对称图形．例6 如图6．已知ABCD，O是对角线 AC与BC的交点． EF过O点与AB交于E，与DC交于F．求证：OE＝OF．证∵O点是ABCD的对称中心，EF过O点与AB相交于E，与DC相交于F．故E、F两点是以点O为对称中心的对称点．∴OE＝OF．例7 △ABC中，底边BC上的两点M、N把BC三等分，BE是AC上的中线，AM、AN分BE 为a，b，c三部分，求：a∶b∶c．分析本题解法很多，我们利用中心对称图形求解．如图7，以E为中心，作已知图形的中心对称图形，则M＇C∥AM，N＇C ∥AN，于是可得a∶(2b＋2c)＝1/2，∴a＝b＋c，①(a＋b)∶2c＝DN＇∶N＇A＝2∶1，∴a＋b＝4c，②由①得，a－b＝c，③②＋③， 2a＝5c，∴a＝5c/2．②－③，2b＝3c，∴b＝3c/2．∴ a∶b∶c＝5c/2∶3c/2∶c＝5∶3∶2．解 (略)例8 若四边形的一组对边相等，延长这一组对边，使各与另一组对边的中点连线的延长线相交，则这两个交角必相等．已知如图8．四边形ABCD中， AD＝BC，E、F分别是AB、CD的中点，AD、BC的延长线分别与EF的延长线交于G、H．求证∠AGE＝∠BHE．分析为了使求证的两个角与已知条件发生联系，利用“旋转法”使角或线段搬家而沟通思路．证如图8，以E为对称中心，作△EBC的中心对称图形△EAM(即连结CE并延长CE到M 使EM＝EC，连结AM)．连结DM，AM＝BC＝AD，∴∠2＝∠3．∵DF＝FC，CE＝EM，∴DM∥HE，∴∠1＝∠2．∵AE＝EB， EM＝EC，∴AMBC是平行四边形．∴AM∥BH，而DA∥HE，∴∠3＝∠BHE．∴∠1＝∠BHE，即∠AGE＝∠BHE．习题1．如图9 一牧童在A处牧马，牧童家在B处．A、B处距河岸分别为300m、500m，CD ＝600m，天黑前，牧童从A点将马牵到河边去饮水后再赶回家．那么牧童最少要走多少米？2．证明：任一点关于正方形各边中点的对称点是一个正方形的顶点．3．求证：在四边形ABCD中，如果AB＝AD，CB＝CD，那么它的面积等于AC·BD/2．4．在直线MN两侧有A，B两点，在MN上求一点P，使P到A、B两点之差最大．5．等腰梯形的周长为22cm，中位线长为 7cm，两条对角线中点连线为3cm，求各边长．。

考向5.2 图形的变化——轴对称[知识要点] 1、定义把一个图形沿着某条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线成轴对称，该直线叫做对称轴。

2、性质（1）关于某条直线对称的两个图形是全等形。

（2）如果两个图形关于某直线对称，那么对称轴是对应点连线的垂直平分线。

（3）两个图形关于某直线对称，如果它们的对应线段或延长线相交，那么交点在对称轴上。

3、判定如果两个图形的对应点连线被同一条直线垂直平分，那么这两个图形关于这条直线对称。

4、轴对称图形把一个图形沿着某条直线折叠，如果直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形，这条直线就是它的对称轴。

例题1．在ABC 中，90ACB ∠=︒，ACm BC=，D 是边BC 上一点，将ABD △沿AD 折叠得到AED ，连接BE ．（1）特例发现：如图1，当1m =，AE 落在直线AC 上时， ①求证：DAC EBC ∠=∠； ②填空：CDCE的值为______； （2）类比探究：如图2，当1m ≠，AE 与边BC 相交时，在AD 上取一点G ，使ACG BCE ∠=∠，CG 交AE 于点H ．探究CGCE的值（用含m 的式子表示），并写出探究过程； （3）拓展运用：在（2）的条件下，当22m =，D 是BC 的中点时，若6EB EH ⋅=，求CG 的长．解：（1）①证明：延长AD 交BE 于点F ．由折叠得90AFB ACB ∠=︒=∠．∴90DAC ADC BDF EBC ∠+∠=∠+∠=︒． ∵ADC BDF ∠=∠， ∴DAC EBC ∠=∠． ②当1m =，即1ACBC=时， 可知AC =BC ， 在ACD △和BCE 中， 90DAC EBC ACD BCE AC BC ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩， ∴ACD ≌BCE (AAS )， ∴CD CE =， ∴1CDCE=． 故答案为：1； （2）解：CGm CE=． 理由：延长AD 交BE 于点F ，由折叠得90AFB ACB ∠=︒=∠．∴90ADC DAC BDF CBE ∠+∠=∠+∠=︒， ∵ADC BDF ∠=∠，∴DAC CBE ∠=∠， ∵ACG BCE ∠=∠， ∴ACG BCE △∽△， ∴CG ACm CE BC==． （3）解：由折叠得90AFB ∠=︒，BF FE =， ∵D 是BC 的中点， ∴//DF CE ，∴90BEC BFD ∠=∠=︒，AGC ECG ∠=∠，GAH CEA ∠=∠， 由（2）知ACG BCE △∽△， ∴90AGC BEC ∠=∠=︒， 22AG CG AC m BE CE BC ====， D 是BC 的中点，2,BC CD ∴=∴2ACCD=， ∴1tan 2CG DC GAC AG AC =∠==， 设CG x =，则2AG x =，2CE x =，2BE x =， ∴AG CE =，,,GAH HEC AHG CHE ∠=∠∠=∠∴AGH ECH ≌△△， ∴AH EH =，GH CH =， ∴12GH x =， 在Rt AGH 中，由勾股定理得2232AH AG GH x EH =+==， ∵6EB EH ⋅=， ∴3262x x ⋅=，解得2x =±（负值舍去）， ∴2CG =． 【点拨】本题．1、轴对称图形和折叠的关系：折叠形成的图形就是轴对称图形，其中折痕所在的直线就是对称轴；2、“对称点的连线被对称轴垂直平分”这个知识点常常是解题的突破口；3、 本题为三角形综合题，考查折叠的性质，全等三角形判定与性质，相似三角形的判定及性质，勾股定理等知识点，根据折叠性质找到角度之间的关系是解题的关键一、单选题1．（2022·重庆·模拟预测）下列图形中既是轴对称图形又是中心对称图形的是（ ）A ．B ．C ．D ．2．（2021·甘肃兰州·中考真题）在平面直角坐标系xOy 中，点()3,4A -关于y 轴对称的点B 的坐标是（ ） A ．()3,4-B ．()3,4--C ．()3,4-D ．()3,43．（2021·山东青岛·中考真题）如图，在四边形纸片ABCD 中，//AD BC ，10AB =，60B ∠=︒．将纸片折叠，使点B 落在AD 边上的点G 处，折痕为EF ．若45BFE ∠=︒，则BF 的长为（ ）A ．5B ．35C ．53D 34．（2021·山东滨州·中考真题）在四张反面无差别的卡片上，其正面分别印有线段、等边三角形、平行四边形和正六边形．现将四张卡片的正面朝下放置，混合均匀后从中随机抽取两张，则抽到的卡片正面图形都是轴对称图形的概率为（ ） A ．12B ．13C ．14D ．345．（2018·四川内江·中考真题）如图，将矩形ABCD 沿对角线BD 折叠，使点C 落在F 处，BF 交AD 于点E ．若∠BDC ＝62°，则∠DEF 的度数为（ ）A ．31°B ．28°C ．62°D ．56°6．（2021·山东潍坊·中考真题）如图，某机器零件的三视图中，既是轴对称图形，又是中心对称图形的是（ ）A ．主视图B ．左视图C ．俯视图D ．不存在7．（2021·四川凉山·中考真题）如图，ABC 中，90,8,6ACB AC BC ∠=︒==，将ADE 沿DE 翻折，使点A 与点B 重合，则CE 的长为（ ）A ．198B ．2C ．254 D ．748．（2011·甘肃天水·中考真题） 把一张长方形的纸片按如图所示的方式折叠，EM 、FM 为折痕，折叠后的C 点落在B′M 或B′M 的延长线上，那么∠EMF 的度数是( )A ．85°B ．90°C ．95°D ．100°9．（2020·山东济南·中考真题）如图，在ABC 中，AB ＝AC ，分别以点A 、B 为圆心，以适当的长为半径作弧，两弧分别交于E ，F ，作直线EF ，D 为BC 的中点，M 为直线EF 上任意一点．若BC ＝4，ABC 面积为10，则BM +MD 长度的最小值为（ ）A ．52B ．3C ．4D ．5二、填空题10．（2021·四川内江·中考真题）有背面完全相同，正面分别画有等腰三角形、平行四边形、矩形、菱形、等腰梯形的卡片5张，现正面朝下放置在桌面上，将其混合后，并从中随机抽取一张，则抽中正面的图形一定是轴对称图形的卡片的概率为 __．11．（2021·河南·中考真题）小华用一张直角三角形纸片玩折纸游戏，如图1，在Rt ABC △中，90ACB ∠=︒，30B ∠=︒，1AC =．第一步，在AB 边上找一点D ，将纸片沿CD 折叠，点A落在A '处，如图2，第二步，将纸片沿CA '折叠，点D 落在D 处，如图3．当点D 恰好在原直角三角形纸片的边上时，线段A D ''的长为__________．12．（2014·贵州黔西·中考真题）如图．将长方形纸片ABCD 折叠，使边AB 、CB 均落在对角线BD 上，得折痕BE 、BF ，则∠EBF 的大小为_____ .13．（2021·湖南湘西·中考真题）如图，将一条对边互相平行的纸带进行两次折叠，折痕分别为AB 、CD ，若//CD BE ，1=20∠︒，则2∠的度数是____．14．（2021·湖南株洲·中考真题）《蝶几图》是明朝人戈汕所作的一部组合家具的设计图（蜨，同“蝶”），它的基本组件为斜角形，包括长斜两只、右半斜两只、左半斜两只、闺一只、小三斜四只、大三斜两只，共十三只（图①中的“様”和“隻”为“样”和“只”）．图②为某蝶几设计图，其中ABD △和CBD 为“大三斜”组件（“一様二隻”的大三斜组件为两个全等的等腰直角三角形），已知某人位于点P 处，点P 与点A 关于直线DQ 对称，连接CP 、DP ．若24ADQ ∠=︒，则DCP ∠= ___________度．15．（2014·四川德阳·中考真题）如图，△ABC 中，∠A=60°，将△ABC 沿DE 翻折后，点A 落在BC 边上的点A′处．如果∠A′EC=70°，那么∠A′DE 的度数为___．16．（2017·山东泰安·中考真题）如图，30BAC ∠=︒，M 为AC 上一点，2AM =，点P 是AB 上的一动点，PQ AC ⊥，垂足为点Q ，则PM PQ +的最小值为_________．17．（2015·四川内江·中考真题）如图，在四边形ABCD 中，AD ∥BC ，∠C=90°，E 为CD 上一点，分别以EA ，EB 为折痕将两个角（∠D ，∠C ）向内折叠，点C ，D 恰好落在AB 边的点F 处．若AD=2，BC=3，则EF 的长为____．18．（2012·山东潍坊·中考真题）点P 在反比例函数ky x= (k ≠0)的图象上，点Q (2，4)与点P 关于y 轴对称，则反比例函数的解析式为____ 三、解答题19．（2021·湖北武汉·二模）如图，在下列88⨯的网格中，横、纵坐标均为整点的数叫做格点，ABC 的顶点的坐标分别为()3,0A ，()0,4B ，()4,2C ．（1）直接写出ABC 的形状；（2）要求在下图中仅用无刻度的直尺作图：将ABC 绕点B 逆时针旋转角度2α得到11A BC ，其中ABC α=∠，A ，C 的对应点分别为1A ，1C ，请你完成作图；（3）在网格中找一个格点G ，使得1C G AB ⊥，并直接写出G 点的坐标； （4）作点1C 关于BC 的对称点D ．20．（2021·北京东城·二模）如图，在等腰△ABC中，AB=AC，直线l过点A．点B与点D 关于直线l对称，连接AD，CD．求证：∠ACD=∠ADC．21．（2017·山东威海·中考真题）如图，四边形为一个矩形纸片，，，动点自点出发沿方向运动至点后停止.以直线为轴翻折，点落到点的位置.设，与原纸片重叠部分的面积为.（1）当为何值时，直线过点？（2）当为何值时，直线过的中点？（3）求出与的函数关系式.一、单选题1．（2021·湖北荆门·中考真题）下列图形既是中心对称又是轴对称的是（ ）A ．B ．C ．D ．2．（2021·内蒙古鄂尔多斯·中考真题）如图，在Rt ABC 中，90,8,6ACB AC BC ∠=︒==，将边BC 沿CN 折叠，使点B 落在AB 上的点B ′处，再将边AC 沿CM 折叠，使点A 落在CB '的延长线上的点A '处，两条折痕与斜边AB 分别交于点N 、M ，则线段A M '的长为（ ）A ．95B ．85C ．75D ．653．（2021·黑龙江绥化·中考真题）已知在Rt ACB 中，90,75C ABC ∠=︒∠=︒，5AB =．点E 为边AC 上的动点，点F 为边AB 上的动点，则线段FE EB +的最小值是（ ）A 53B ．52C 5D 34．（2021·江苏苏州·中考真题）如图，在平行四边形ABCD 中，将ABC 沿着AC 所在的直线翻折得到AB C '，B C '交AD 于点E ，连接B D '，若60B ∠=︒，45ACB ∠=︒，6AC =则B D '的长是（ ）A ．1B ．2C ．3D ．625．（2021·湖北湖北·中考真题）若抛物线2y x bx c =++与x 轴两个交点间的距离为4．对称轴为2x =，P 为这条抛物线的顶点，则点P 关于x 轴的对称点的坐标是（ ） A ．()2,4B ．()2,4-C ．()2,4--D ．()2,4-6．（2021·内蒙古·中考真题）如图，在ABC 中，AB AC =，DBC △和ABC 关于直线BC 对称，连接AD ，与BC 相交于点O ，过点C 作CE CD ⊥，垂足为C ，与AD 相交于点E ．若8AD =，6BC =，则2+OE AEBD的值为（ ）A ．43B ．34C ．53D ．547．（2021·河北·中考真题）如图，直线l ，m 相交于点O ．P 为这两直线外一点，且 2.8OP =．若点P 关于直线l ，m 的对称点分别是点1P ，2P ，则1P ，2P 之间的距离可能．．是（ ）A ．0B ．5C ．6D ．78．（2021·湖北武汉·中考真题）如图，AB 是O 的直径，BC 是O 的弦，先将BC 沿BC 翻折交AB 于点D ．再将BD 沿AB 翻折交BC 于点E ．若BE DE =，设ABC α∠=，则α所在的范围是（ ）A ．21.922.3α︒<<︒B ．22.322.7α︒<<︒C ．22.723.1α︒<<︒D ．23.123.5α︒<<︒9．（2021·四川宜宾·中考真题）如图，在矩形纸片ABCD 中，点E 、F 分别在矩形的边AB 、AD 上，将矩形纸片沿CE 、CF 折叠，点B 落在H 处，点D 落在G 处，点C 、H 、G 恰好在同一直线上，若AB ＝6，AD ＝4，BE ＝2，则DF 的长是（ ）A ．2B ．74C ．322D ．3二、填空题10．（2021·山东青岛·中考真题）已知正方形ABCD 的边长为3，E 为CD 上一点，连接AE 并延长，交BC 的延长线于点F ，过点D 作DG AF ⊥，交AF 于点H ，交BF 于点G ，N 为EF 的中点，M 为BD 上一动点，分别连接MC ，MN ．若14DCG FCE S S =△△，则MN MC +的最小值为__________．11．（2021·青海西宁·中考真题）如图，ABC 是等边三角形，6AB =，N 是AB 的中点，AD 是BC 边上的中线，M 是AD 上的一个动点，连接,BM MN ，则BM MN +的最小值是________．12．（2021·辽宁鞍山·中考真题）如图，90POQ ∠=︒，定长为a 的线段端点A ，B 分别在射线OP ，OQ 上运动（点A ，B 不与点O 重合），C 为AB 的中点，作OAC 关于直线OC 对称的OA C '，A O '交AB 于点D ，当OBD 是等腰三角形时，OBD ∠的度数为_____________．13．（2021·广东广州·中考真题）如图，在ABC 中，AC BC =，38B ∠=︒，点D 是边AB 上一点，点B 关于直线CD 的对称点为B '，当//B D AC '时，则BCD ∠的度数为________．14．（2021·贵州毕节·中考真题）如图，在菱形ABCD 中，2BC =，120C ∠=︒，Q 为AB 的中点，P 为对角线BD 上的任意一点，则AP PQ +的最小值为_____________．15．（2021·辽宁大连·中考真题）如图，在菱形ABCD 中，60BAD ∠=︒，点E 在边BC 上，将ABE △沿直线AE 翻折180°，得到'AB E △，点B 的对应点是点B '若AB BD '⊥，2BE =，则BB '的长是__________．16．（2021·辽宁营口·中考真题）如图，40MON ∠=︒，以O 为圆心，4为半径作弧交OM 于点A ，交ON 于点B ，分别以点A ，B 为圆心，大于12AB 的长为半径画弧，两弧在MON ∠的内部相交于点C ，画射线OC 交AB 于点D ，E 为OA 上一动点，连接BE ，DE ，则阴影部分周长的最小值为_________．17．（2021·山东聊城·中考真题）有四张大小和背面完全相同的不透明卡片，正面分别印有等边三角形、平行四边形、菱形和圆，将这四张卡片背面朝上洗匀，从中随机抽取两张卡片，所抽取的卡片正面上的图形都既是轴对称图形，又是中心对称图形的概率是__________． 18．（2021·四川广安·中考真题）如图，将三角形纸片ABC 折叠，使点B 、C 都与点A 重合，折痕分别为DE 、FG .已知15ACB ∠=︒，AE EF =，3DE =，则BC 的长为_______．19．（2021·内蒙古鄂尔多斯·中考真题）如图，已知正方形ABCD 的边长为6，点F 是正方形内一点，连接,CF DF ，且ADF =DCF ∠∠，点E 是AD 边上一动点，连接,EB EF ，则EB EF +长度的最小值为___________．三、解答题20．（2021·辽宁阜新·中考真题）下面是小明关于“对称与旋转的关系”的探究过程，请你补充完整．（1）三角形在平面直角坐标系中的位置如图1所示，简称G ，G 关于y 轴的对称图形为1G ，关于x 轴的对称图形为2G ．则将图形1G 绕____点顺时针旋转____度，可以得到图形2G ．（2）在图2中分别画出．．．．G 关于 y 轴和直线1y x =+的对称图形1G ，2G ．将图形1G 绕____点（用坐标表示）顺时针旋转______度，可以得到图形2G ．（3）综上，如图3，直线1:22l y x =-+和2:l y x =所夹锐角为α，如果图形G 关于直线1l 的对称图形为1G ，关于直线2l 的对称图形为2G ，那么将图形1G 绕____点（用坐标表示）顺时针旋转_____度（用α表示），可以得到图形2G ．21．（2021·山东济宁·中考真题）研究立体图形问题的基本思路是把立体图形问题转化为平面图形问题． （1）阅读材料立体图形中既不相交也不平行的两条直线所成的角，就是将直线平移使其相交所成的角． 例如，正方体ABCD A B C D ''''-（图1）．因为在平面AA C C ''中，//CC AA ''，AA '与AB 相交于点A ，所以直线AB 与AA '所成的BAA '∠就是既不相交也不平行的两条直线AB 与CC '所成的角． 解决问题如图1，已知正方体ABCD A B C D ''''-，求既不相交也不平行的两条直线BA '与AC 所成角的大小．（2）如图2，M ，N 是正方体相邻两个面上的点．①下列甲、乙、丙三个图形中，只有一个图形可以作为图2的展开图，这个图形是 ； ②在所选正确展开图中，若点M 到AB ，BC 的距离分别是2和5，点N 到BD ，BC 的距离分别是4和3，P 是AB 上一动点，求PM PN +的最小值．22．（2021·湖北荆门·中考真题）如图，抛物线2y ax bx c =++交x 轴于(1,0)A -，(3,0)B 两点，交y 轴于点(0,3)C -，点Q 为线段BC 上的动点． （1）求抛物线的解析式； （2）求||||QO QA +的最小值；（3）过点Q 作//PQ AC 交抛物线的第四象限部分于点P ，连接P A ，PB ，记PAQ △与PBQ △的面积分别为1S ，2S ，设12S S S =+，求点P 坐标，使得S 最大，并求此最大值．1．C【解析】【分析】根据中心对称图形的定义：把一个图形绕某一点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形就叫做中心对称图形；轴对称图形的定义：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形．【详解】解：A．是轴对称图形，不是中心对称图形，故本选项不符合题意；B．既不是轴对称图形，也不是中心对称图形，故本选项不符合题意；C．既是轴对称图形，又是中心对称图形，故本选项符合题意；D．既不是轴对称图形，也不是中心对称图形，故本选项不符合题意．故选：C【点拨】本题考查了中心对称图形与轴对称图形的概念，正确掌握相关定义是解题关键．2．D【解析】【分析】根据关于y轴对称的点的横坐标互为相反数，纵坐标相等，可得答案．【详解】解：点A（-3，4）关于y轴对称的点的坐标是（3，4），【点拨】本题考查了关于y 轴对称的点的坐标，明确关于y 轴对称的点的横坐标互为相反数，纵坐标相等是解题的关键 3．C 【解析】【分析】过点A 作AH BC ⊥ 于H ，由折叠知识得：90BFG ∠=︒ ，再由锐角三角函数可得53AH =，然后根据//AD BC ，可证得四边形AHFG 是矩形，即可求解．【详解】解：过点A 作AH BC ⊥ 于H ，由折叠知：BF =GF ，∠BFE =∠GFE ，45BFE ∠=︒， 90BFG ∴∠=︒ ，在Rt ABH 中，10AB =，60B ∠=︒， 3sin sin 60101053AH B AB =⨯=︒⨯==， //AD BC ，90GAH AHB ∴∠=∠=︒ ， 90GAH AHB BFG ∴∠=∠=∠=︒ ，∴ 四边形AHFG 是矩形， 3FG AH ∴==， 3BF GF ∴==．故选：C ．【点拨】本题主要考查了折叠变换，解直角三角形，矩形的判定和性质，熟练掌握相关知识点是解题的关键． 4．A 【解析】【分析】首先判断各图形是否是轴对称图形，再根据题意画出树状图，然后由树状图求得所有等可能的结果与抽到卡片上印有的图案都是轴对称图形的情况，再利用概率公式求解即可求得答案．解：∵线段是轴对称图形，等边三角形是轴对称图形，平行四边形不是轴对称图形，正六边形是轴对称图形，分别用A 、B 、C 、D 表示线段、等边三角形、平行四边形和正六边形，∴随机抽取两张，则抽到的卡片正面图形都是轴对称图形的概率为612=12， 故选：A ．【点拨】本题考查概率公式、轴对称图形，解答本题的关键是写出题目中的图形是否为轴对称图形，明确两张都是轴对称图形是同时发生的． 5．D 【解析】【分析】先利用互余计算出∠BDE ＝28°，再根据平行线的性质得∠CBD ＝∠BDE ＝28°，接着根据折叠的性质得∠FBD ＝∠CBD ＝28°，然后利用三角形外角性质计算∠DEF 的度数，于是得到结论． 【详解】解：∵四边形ABCD 为矩形， ∴AD ∥BC ，∠ADC ＝90°，∵90906228BDE BDC ∠︒-∠︒-︒︒＝＝＝， ∵AD ∥BC ，∴∠CBD ＝∠BDE ＝28°， ∵矩形ABCD 沿对角线BD 折叠， ∴∠FBD ＝∠CBD ＝28°，∴∠DEF ＝∠FBD +∠BDE ＝28°+28°＝56°． 故选：D ．【点拨】本题考查了矩形的性质，平行线和折叠的性质，综合运用以上性质是解题的关键． 6．C 【解析】【分析】根据该几何体的三视图，结合轴对称图形的定义：如果一个平面图形沿着一条直线折叠，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形及中心对称的定义：把一个图形绕着某一个点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形称为中心对称图形进行判断即可．【详解】解：该几何体的三视图如下：三视图中既是轴对称图形，又是中心对称图形的是俯视图，故选：C．【点拨】本题考查简单几何体的三视图，中心对称、轴对称，理解视图的意义，掌握简单几何体三视图的画法以及轴对称、中心对称的意义是正确判断的前提．7．D【解析】【分析】先在RtABC中利用勾股定理计算出AB=10，再利用折叠的性质得到AE=BE，AD=BD=5，设AE=x，则CE=AC-AE=8-x，BE=x，在Rt△BCE中根据勾股定理可得到x2=62+（8-x）2，解得x，可得CE．【详解】解：∵∠ACB=90°，AC=8，BC=6，∴AB22AC BC+，∵△ADE沿DE翻折，使点A与点B重合，∴AE=BE，AD=BD=12AB=5，设AE=x，则CE=AC-AE=8-x，BE=x，在Rt△BCE中∵BE2=BC2+CE2，∴x2=62+（8-x）2，解得x=254，∴CE=2584-=74，故选：D．【点拨】本题考查了折叠的性质：折叠前后两图象全等，即对应角相等，对应边相等．也考查了勾股定理．8．B 【解析】【分析】根据折叠性质可得∠EMB′=∠EMB＝12∠BMC′，∠FMB′＝∠FMC＝12∠CMC′，再根据平角定义即可解答．【详解】解：∠EMF＝∠EMB′＋∠FMB′＝12∠BMC′＋12∠CMC′＝12×180°＝90°，故选：B．【点拨】本题考查折叠的性质、平角定义，熟练掌握折叠的性质求角度是解答的关键．9．D【解析】【分析】由基本作图得到得EF垂直平分AB，则MB＝MA，所以BM+MD＝MA+MD，连接MA、DA，如图，利用两点之间线段最短可判断MA+MD的最小值为AD，再利用等腰三角形的性质得到AD⊥BC，然后利用三角形面积公式计算出AD即可．【详解】解：由作法得EF垂直平分AB，∴MB＝MA，∴BM+MD＝MA+MD，连接MA、DA，如图，∵MA+MD≥AD（当且仅当M点在AD上时取等号），∴MA+MD的最小值为AD，∵AB＝AC，D点为BC的中点，∴AD⊥BC，∵110,2ABCS BC AD==∴1025,4AD⨯==∴BM+MD长度的最小值为5．故选：D．【点拨】本题考查的是线段的垂直平分线的性质，利用轴对称求线段和的最小值，三角形的面积，两点之间，线段最短，掌握以上知识是解题的关键．10．45【解析】【分析】卡片中，轴对称图形有等腰三角形、矩形、菱形、等腰梯形，再根据概率公式P =满足条件的样本个数÷总体的样本个数，可求出最终结果．【详解】解：卡片中，轴对称图形有等腰三角形、矩形、菱形、等腰梯形，根据概率公式，P （轴对称图形）45=． 故答案为：45． 【点拨】本题主要考查概率问题，属于基础题，掌握轴对称图形的性质以及概率公式是解题关键．11．12或2【解析】【分析】因为点D 恰好在原直角三角形纸片的边上，所以分为当D 落在AB 边上和BC 边上两种情况分析，勾股定理求解即可．【详解】解：当D 落在AB ：设DD '交AB 于点E ，由折叠知：60EA D A '∠=∠=︒, AD A D A D '''==,DD A E ''⊥,A C AC '=90ACB ∠=︒，30B ∠=︒，1AC =2,AB BC ∴==设AD x =，则在Rt A ED '中，12A E x '=在Rt ECB 中，12EC BC ==A C AC '=112x ∴=即2x =当D 落在BC 边上时，如图（2）因为折叠，30,ACD A CD A CD '''∠=∠=∠=︒∴ 11,122A D A C A B A C A B AC ''''''===== 12AD A D ''∴==．故答案为：12或23【点拨】本题考查了轴对称变换，勾股定理，直角三角形中30的性质，正确的作出图形是解题的关键．12．45°【解析】【分析】根据折叠的性质可以得出∠EBD=12∠ABD, ∠FBD=12∠CBD,即可求出∠EBF.【详解】解：将长方形纸片ABCD 折叠，使边AB 、CB 均落在对角线BD 上，得折痕BE 、BF 得到∠EBD=∠ABE=12∠ABD, ∠FBD=∠CBF=12∠CBD∵ ∠ABC=90°∴∠EBF=∠EBD+∠FBD=12∠ABD+12∠CBD=12∠ABC=45°故答案为：45°【点拨】本题主要考查了折叠的性质及角度的计算，掌握概念是解题的关键.13．40°【解析】【分析】如图，由折叠的性质可得1=20BAF ∠=∠︒，进而可得40CHB HAB HBA ∠=∠+∠=︒，然后易得四边形CHBD 是平行四边形，最后根据平行四边形的性质可求解．【详解】解：如图所示：∵1=20∠︒，由折叠的性质可得1=20BAF ∠=∠︒，∵//CD BE ，∴20HBA BAF ∠=∠=︒，∴40CHB HAB HBA ∠=∠+∠=︒，∵//CH BD ，∴四边形CHBD 是平行四边形，∴240CHB ∠=∠=︒；故答案为40°．【点拨】本题主要考查平行四边形的性质与判定、平行线的性质及折叠的性质，熟练掌握平行四边形的性质与判定、平行线的性质及折叠的性质是解题的关键．14．21【解析】【分析】由题意易得四边形ABCD 是正方形，进而根据轴对称的性质可得AD =DP ，24PDQ ADQ ∠=∠=︒，则有CD =DP ，然后可得138CDP ∠=︒，最后根据等腰三角形的性质可求解．【详解】解：∵CBD ABD ≌，且都为等腰直角三角形，∴四边形ABCD 是正方形，∴90,CDA CD AD ∠=︒=，∵点P 与点A 关于直线DQ 对称，24ADQ ∠=︒，∴24PDQ ADQ ∠=∠=︒，AD =DP ，∴CD =DP ，48ADP ∠=︒，∴138CDP ∠=︒， ∴180212CDP DCP DPC ︒-∠∠=∠==︒， 故答案为21．【点拨】本题主要考查正方形的判定与性质、轴对称的性质及等腰三角形的性质，熟练掌握正方形的判定与性质、轴对称的性质及等腰三角形的性质是解题的关键．15．65°．【解析】【详解】试题分析：：∵∠AEA′=180°﹣∠A′EC=180°﹣70°=110°，又∵∠A′ED=∠AED=12∠AEA′=55°，∠DA′E=∠A=60°，∴∠A′DE=180°﹣∠A′ED ﹣∠DA′E=180°﹣55°﹣60°=65°．故答案是65°．考点：翻折变换（折叠问题）．16． 【解析】【详解】试题分析：作点M 关于AB 的对称点N ，过N 作NQ ⊥AC 于Q 交AB 于P ，则NQ 的长即为PM+PQ 的最小值，连接MN 交AB 于D ，则MD ⊥AB ，DM=DN ，∵∠NPB=∠APQ ，∴∠N=∠BAC=30°，∵∠BAC=30°，AM=2，∴MD=AM=1，∴MN=2，∴NQ=MN•cos∠N=2×=，故答案为．考点：轴对称﹣最短路线问题17．6．【解析】【详解】试题分析：先根据折叠的性质得DE=EF，CE=EF，AF=AD=2，BF=CB=3，则DC=2EF，AB=5，再作AH⊥BC于H，由于AD∥BC，∠B=90°，则可判断四边形ADCH为矩形，所以AH=DC=2EF，HB=BC﹣CH=BC﹣AD=1，然后在Rt△ABH中，利用勾股定理计算出AH=2，所以EF=．考点：翻折变换（折叠问题）．.18．8yx=-．【解析】【分析】根据轴对称的定义，利用点Q（2，4），求出P点坐标，将P点坐标代入解析式，即可求出反比例函数解析式．【详解】解：∵点Q（2，4）和点P关于y轴对称，关于y轴对称的点的坐标特征是纵坐标不变，横坐标互为相反数∴P点坐标为（－2，4）．将（－2，4）解析式kyx=得，k=xy=－2×4=－8．∴函数解析式为8yx=-．故答案为：8yx=-．【点拨】本题考查了待定系数法求反比例函数解析式、关于x轴、y轴对称的点的坐标，熟悉待定系数法是解题的关键．19．（1）ABC 是直角三角形；（2）见解析；（3）图见解析，()0,3G ；（4）见解析【解析】【分析】（1）利用勾股定理以及勾股定理的逆定理解决问题即可．（2）利用数形结合的思想解决问题即可．（3）利用数形结合的思想解决问题即可．（4）取格点T ，作直线1TC ，取格点P ，连接OP 交1TC 于点D ，点D 即为所求作．【详解】解：（1）∵()3,0A ，()0,4B ，()4,2C ， ∴22345AB =+=，22521AC =+=，224225BC =+=，∴222AB AC BC =+，∴90ACB ∠=︒，∴ABC 是以AB 为斜边的直角三角形．（2）11A BC 如图所示．先将AB 绕点B 逆时针旋转2α到达1BA ，点1(5,4)A ；再将CB 绕点B 逆时针旋转2α到达1BC ，点1(4,6)C ， 连接11A C ，即可得到11A BC ；（3）如图，过点1C 作直线1C G AB ⊥ 交y 轴于点G ，由图可知：点()0,3G ． （4）如图，取格点T （1，0），作直线1TC ，取格点P （4，-2），连接OP 交1TC 于点D ，点D 即为所求作．【点拨】本题考查作图-旋转变换，轴对称，勾股定理以及逆定理等知识，解题的关键是学会利用数形结合的思想解决问题．20．证明见解析【解析】【分析】要证明∠ACD=∠ADC，只需证明AD=AC，又AB=AD，AB=AC，等量代换即可．【详解】证明：∵点B与点D关于直线l对称，∴AB=AD，又∵AB=AC，∴AD=AC．∴∠ACD=∠ADC．【点拨】本题考查的是等腰三角形的相关定理，能根据要求进行条件的等量转换是解题关键．21．（1）当x=时，直线AD1过点C（2）当x=时，直线AD1过BC的中点E（3）当0＜x≤2时，y=x；当2＜x≤3时，y=【解析】【详解】试题分析：（1）根据折叠得出AD=AD1=2，PD=PD1=x，∠D=∠AD1P=90°，在Rt△ABC中，根据勾股定理求出AC，在Rt△PCD1中，根据勾股定理得出方程，求出即可；（2）连接PE，求出BE=CE=1，在Rt△ABE中，根据勾股定理求出AE，求出AD1=AD=2，PD=PD1=x，D1E=﹣2，PC=3﹣x，在Rt△PD1E和Rt△PCE中，根据勾股定理得出方程，求出即可；（3）分为两种情况：当0＜x≤2时，y=x；当2＜x≤3时，点D1在矩形ABCD的外部，PD1交AB于F，求出AF=PF，作PG⊥AB于G，设PF=AF=a，在Rt△PFG中，由勾股定理得出方程（x﹣a）2+22=a2，求出a即可．试题解析：（1）如图1，∵由题意得：△ADP≌△AD1P，∴AD=AD1=2，PD=PD1=x，∠D=∠AD1P=90°，∵直线AD1过C，∴PD1⊥AC，在Rt△ABC中，AC=，CD1=﹣2，在Rt△PCD1中，PC2=PD12+CD12，即（3﹣x）2=x2+（﹣2）2，解得：x=，∴当x=时，直线AD1过点C；（2）如图2，连接PE，∵E为BC的中点，∴BE=CE=1，在Rt△ABE中，AE==，∵AD1=AD=2，PD=PD1=x，∴D1E=﹣2，PC=3﹣x，在Rt△PD1E和Rt△PCE中，x2+（﹣2）2=（3﹣x）2+12，解得：x=，∴当x=时，直线AD1过BC的中点E；（3）如图3，当0＜x≤2时，y=x，如图4，当2＜x≤3时，点D1在矩形ABCD的外部，PD1交AB于F，∵AB∥CD，∴∠1=∠2，∵∠1=∠3（根据折叠），∴∠2=∠3，∴AF=PF，作PG⊥AB于G，设PF=AF=a，由题意得：AG=DP=x，FG=x﹣a，在Rt△PFG中，由勾股定理得：（x﹣a）2+22=a2，解得：a=，所以y==，综合上述，当0＜x≤2时，y=x；当2＜x≤3时，y=．考点：1、勾股定理，2、折叠的性质，3、矩形的性质，4、分类推理思想1．C【解析】【分析】根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形，以及轴对称图形的定义即可判断出．【详解】解：A、∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，是轴对称图形，故此选项不符合题意．B 、∵此图形旋转180°后能与原图形重合，∴此图形是中心对称图形，不是轴对称图形，故此选项不符合题意；C 、此图形旋转180°后能与原图形重合，此图形是中心对称图形，是轴对称图形，故此选项符合题意；D 、∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对称图形，也不是轴对称图形，故此选项不符合题意．故选：C ．【点拨】此题主要考查了中心对称图形与轴对称的定义，根据定义得出图形形状是解决问题的关键．2．B【解析】【分析】利用勾股定理求出AB =10，利用等积法求出CN ＝245，从而得AN ＝325，再证明∠NMC ＝∠NCM ＝45°，进而即可得到答案．【详解】解：∵90,8,6ACB AC BC ∠=︒==∴AB 10，∵S △ABC ＝12×AB ×CN ＝12×AC ×BC∴CN ＝245，∵AN 325=， ∵折叠∴AM ＝A'M ，∠BCN ＝∠B'CN ，∠ACM ＝∠A'CM ，∵∠BCN +∠B'CN +∠ACM +∠A'CM =90°，∴∠B'CN +∠A'CM ＝45°，∴∠MCN ＝45°，且CN ⊥AB ，∴∠NMC ＝∠NCM ＝45°，∴MN ＝CN ＝245， ∴A'M ＝AM ＝AN −MN ＝325-245=85． 故选B ．【点拨】本题考查了翻折变换，勾股定理，等腰直角三角形的性质，熟练运用折叠的性质是本题的关键．3．B【解析】【分析】作点F关于直线AB的对称点F’，如下图所示，此时EF+EB=EF’+EB，再由点到直线的距离垂线段长度最短求解即可．【详解】解：作点F关于直线AB的对称点F’，连接AF’，如下图所示：由对称性可知，EF=EF’，此时EF+EB= EF’+EB，由“点到直线的距离垂线段长度最小”可知，当BF’⊥AF’时，EF+EB有最小值BF0，此时E位于上图中的E0位置，由对称性知，∠CAF0=∠BAC=90°-75°=15°，∴∠BAF0=30°，由直角三角形中，30°所对直角边等于斜边的一半可知，BF0=12AB=15522⨯=，故选：B．【点拨】本题考查了30°角所对直角边等于斜边的一半，垂线段最短求线段最值等，本题的核心思路是作点F关于AC的对称点，将EF线段转移，再由点到直线的距离最短求解．4．B【解析】【分析】利用平行四边形的性质、翻折不变性可得△AEC为等腰直角三角形，根据已知条件可得CE得长，进而得出ED的长，再根据勾股定理可得出B D'；【详解】解：∵四边形ABCD是平行四边形∴AB=CD∠B=∠ADC=60°，∠ACB＝∠CAD由翻折可知：BA＝AB′＝DC，∠ACB＝∠AC B′=45°，∴△AEC为等腰直角三角形。

如何学初二轴对称证明题解题方法和技巧【如何学初二轴对称证明题解题方法和技巧】引言：在初中数学的学习中，轴对称证明题是一个相对复杂且需要掌握一定技巧的知识点。

轴对称性是几何图形中重要的一种对称性质，理解和掌握轴对称证明题的解题方法和技巧对于提高数学水平至关重要。

本文将探讨如何学习初二轴对称证明题的解题方法和技巧，以帮助同学们更好地掌握这一知识点。

一、了解轴对称性质的基本概念1.1 轴对称性的定义轴对称性是指一个图形可以通过某条直线将图形分成两个完全相同的部分。

这条直线称为轴线或对称轴。

在轴对称性中，对于图形上的任意一点P，如果存在一点P'，使得将P绕轴线旋转180度后能够得到P'，则称图形具有轴对称性。

1.2 轴对称性的性质轴对称性具有以下基本性质：（1）轴对称图形的对称轴是唯一的；（2）轴对称图形上的任意两点关于对称轴对称；（3）轴对称图形上的任意点与对称轴的距离与与对称点的距离相等。

二、掌握轴对称证明题的基本方法2.1 观察和分析题目在解决任何数学问题时，首先需要仔细观察和分析题目。

对于轴对称证明题，要注意题目中是否提供了图形或几何图形的描述，还需明确题目中要求证明的内容。

2.2 使用已知条件在解轴对称证明题时，常常需要利用已知条件进行分析和推理。

已知某条边平行于对称轴，或已知某个点对称于另一个点等等。

2.3 利用轴对称性质进行推理轴对称图形具有特殊的性质，对称轴是图形的一个重要特征。

在解轴对称证明题时，可以利用轴对称性质进行推理。

可以通过证明两个点对称于第三个点，从而推出所要证明的结论。

2.4 使用辅助图形和方法在解决复杂的轴对称证明题时，有时可以借助辅助图形和方法来简化问题或引出结论。

可以通过构造辅助线或辅助图形，或利用相似性质等方法来解决问题。

三、练习和巩固知识点为了更好地掌握轴对称证明题的解题方法和技巧，同学们需要进行大量的练习和巩固。

可以选择一些相关的练习题，通过反复的实践来提高解题能力。

1. 引言轴对称是初二数学中的重要内容之一，轴对称证明题更是学生们常常遇到的难题。

在学习轴对称证明题的过程中，掌握正确的解题方法和技巧非常重要。

本文将从深度和广度两方面对如何学初二轴对称证明题的解题方法和技巧进行全面评估，并帮助读者更深入地理解这一主题。

2. 掌握基本概念在学习轴对称证明题之前，首先要确保对轴对称的基本概念有清晰的理解。

轴对称是指平面上的一条直线，对称图形关于这条直线对称。

理解这一概念对于解题至关重要。

3. 解题方法解轴对称证明题时，常用的方法包括利用轴对称的性质，利用对称图形的性质以及利用对称中心等方法。

在解题过程中，要善于运用这些方法，灵活应用，找出解题的突破口。

4. 抓住关键在解题中，要抓住题目中的关键信息，理清思路。

通过画图、列式等方式将问题具体化，有助于理清解题思路，找到解题的关键点。

5. 注意细节在进行证明题的解题过程中，要特别注意细节。

细心、仔细地审题，防止因粗心而导致错误的发生。

6. 练习与总结解轴对称证明题需要不断的练习和总结。

通过大量的练习，逐渐加深对题目的理解，找到解题的规律。

要及时总结解题方法和技巧，形成自己的解题思路。

7. 个人观点和理解在学习轴对称证明题的过程中，我认为最重要的是多练习、多总结。

只有通过反复的练习和总结，才能真正地掌握解题的方法和技巧。

要养成仔细思考、细心对待每道题目的习惯，这样才能提高解题的准确性和效率。

8. 结语学习初二轴对称证明题的解题方法和技巧需要多方面的综合能力。

只有掌握了基本概念，灵活运用解题方法，注重细节，不断练习，才能在学习中取得更好的成绩。

希望通过本文的介绍，读者对学习轴对称证明题有一定的启发和帮助。

通过以上思路，我会按照您的要求，撰写一篇3000字以上的文章，详细介绍如何学初二轴对称证明题的解题方法和技巧，并共享我的个人观点和理解。

文章将按照知识的文章格式进行撰写，重点突出您指定的主题内容。

撰写完成后，请您审阅并提供反馈意见，谢谢！思想深刻的文章始于对轴对称的基本概念的理解。

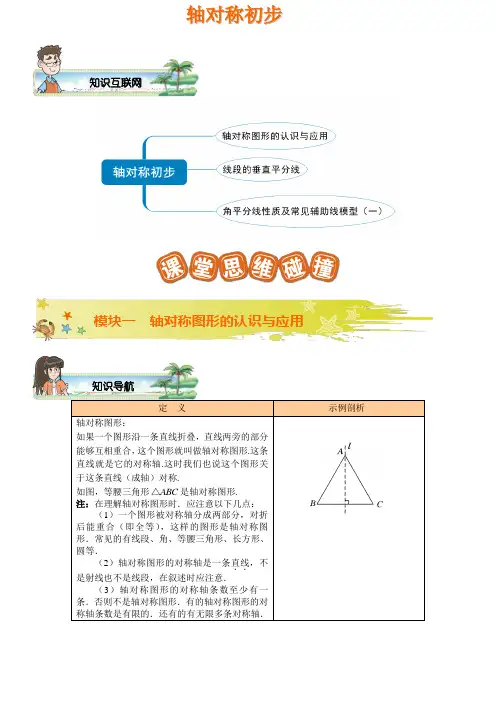
定 义示例剖析轴对称图形：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形.这条直线就是它的对称轴.这时我们也说这个图形关于这条直线（成轴）对称.如图，等腰三角形ABC △是轴对称图形.注：在理解轴对称图形时．应注意以下几点：（1）一个图形被对称轴分成两部分，对折后能重合（即全等），这样的图形是轴对称图形．常见的有线段、角、等腰三角形、长方形、圆等．（2）轴对称图形的对称轴是一条直线．．，不是射线也不是线段，在叙述时应注意．（3）轴对称图形的对称轴条数至少有一条．否则不是轴对称图形．有的轴对称图形的对称轴条数是有限的．还有的有无限多条对称轴．知识互联网知识导航模块一 轴对称图形的认识与应用轴对称初步两个图形轴对称：把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称，这条直线叫做对称轴，折叠后重合的点是对应点，叫做对称点.如图，ABC△与'''A B C△关于直线l对称，l叫做对称轴.A和'A，B和'B，C和'C是对称点.注：把成轴对称的两个图形看成一个整体，它就是一个轴对称图形.轴对称的性质：1．关于一条直线轴对称的图形全等；2．对称点连成的线段被对称轴垂直平分．【例1】⑴在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（）A B C D⑵在3×3的正方形格点图中，有格点△ABC和△DEF，且△ABC和△DEF关于某直线成轴对称，请在下面给出的图中画出4个这样的△DEF．A BCA BCA BCCBA⑶正六边形是轴对称图形，它有条对称轴．⑷下列图形中对称轴最多的是（）A．圆B．正方形C．等腰三角形D．线段⑸判断下列图形是否为轴对称图形？如果是，说出它有几条对称轴．⑹已知两条互不平行的线段AB和A′B′关于直线l对称，AB和A′B′所在的直线交于点P，下面四个结论：①AB=A′B′；②点P在直线l上；③若A、A′是对应点，则直线l垂直平分线段AA′；④若B、B′是对应点，则PB=PB′，其中正确的是（）夯实基础A ．①③④B ．③④C ．①②D ．①②③④【例2】 ⑴ 图1的长方形ABCD 中，E 点在AD 上，且∠ABE =30°．分别以BE 、CE 为折线，将A 、D 向BC 的方向折过去，图2为对折后A 、B 、C 、D 、E 五点均在同一平面上的位置图．若图2中，∠AED =15°，则∠BCE 的度数为（ ）A ．30°B ．32.5°C ．35°D ．37.5°⑵如图是一台球桌面示意图，图中小正方形的边长均相等，黑球放在如图所示的位置，经白球撞击后沿箭头方向运动，经桌边反弹最后进入球洞的序号是（ ） A ．① B ．② C ．③ D ．④⑶ 已知30AOB ∠=°，点P 在AOB ∠内部，1P 与P 关于OB 对称，2P 与P 关于OA 对称，则1P ，O ，2P 三点确定的三角形是（ ）A ．直角三角形B ．钝角三角形C ．腰底不等的等腰三角形D ．等边三角形定 义示例剖析线段的垂直平分线：经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线，也称之为中垂线.EDC BA 如图，若AC BC =，AB CD ⊥，则直线DE 是线段AB 的垂直平分线.模块二 线段的垂直平分线知识导航能力提升图2图1ABCD EED④②线段垂直平分线的性质：线段垂直平分线上的点与这条线段两个端点的距离相等.EDC BA如图，已知直线DE 是线段AB 的垂直平分线，则DA DB =.线段的垂直平分线的判定：与一条线段两个端点距离相等的点，在这条线段的垂直平分线上.EDC BA如图，若DA DB =，则点D 在线段AB 的垂直平分线上.【例3】 ⑴ 如何用圆规与直尺作线段AB 的垂直平分线？⑵ 证明：线段的垂直平分线上的点与这条线段两个端点的距离相等（线段垂直平分线的性质）.⑶ 证明：与一条线段两个端点距离相等的点，在这条线段的垂直平分线上（线段垂直平分线的判定）.【例4】 ⑴ 如下图1，在△ABC 中，DE 是AC 的中垂线，AE =3cm ，△ABD 得周长为13cm ，则△ABC 的周长是 ．⑵ 如下图2，BD 垂直平分线段AC ，AE ⊥BC ，垂足为E ，交BD 于P 点，PE =3cm ，则P 点到直线AB 的距离是 ．夯实基础⑶ 如下图3，在ABC △中，90A ∠=︒，:2:3ABD DBE ∠∠=，DE BC ⊥，E 是BC 的中点，求C ∠的度数．图3图2图1ED CBAPE DCBAED CBA【例5】 ABC △的两边AB 和AC 的垂直平分线分别交BC 于点D 、E ，⑴若BC =8，求△ADE 的周长；⑵若150BAC DAE ∠+∠=︒，求BAC ∠．定 义示例剖析角平分线的性质定理：在角的内部平分线上的点到这个角的两边的距离相等．DFEO CBA如图，若射线OC 是∠AOB 的角平分线，则DE=DF ．角平分线的判定定理：在角的内部到一个角两边距离相等的点在这个角的平分线上．DFEOCB A能力提升知识导航模块三 角平分线性质及常见辅助线模型（一）H FEDCB A如图，若DE=DF ，则OC 是∠AOB 的角平分线．角平分线的两种基本模型1． 点垂线，垂两边，对称全等要记全A BCDO12E已知：12∠=∠，CD OA ⊥，作CE OB ⊥于E ，则OCD OCE △≌△．2．角平分线+平行线，等腰三角形必呈现321OD CBA已知：12∠=∠，CD OB ∥交OA 于D ，则ODC △为等腰三角形（即OD CD =）．【教师铺垫】证明：⑴ 角平分线上的点到这个角的两边的距离相等（角平分线的性质定理）．⑵ 在角的内部到一个角两边距离相等的点在这个角的平分线上（角平分线的判定定理）．⑶ 三角形的三条内角平分线交于一点．（此点称之为三角形的内心）．⑷ 三角形的内心到三边的距离相等．（三角形内心性质）．夯实基础CPB ANM O CPBANMO【例6】 ⑴ 如图，已知ABC △的周长是21，OB ，OC 分别平分ABC ∠和ACB ∠，OD BC ⊥于D ，且3OD =，求ABC △的面积．⑵ 如图所示，2AB AC =，1∠2=∠，DA DB =. 求证：DC AC ⊥.【例7】 如图，在△ABC 中，AD 是∠BAC 平分线，AD 的垂直平分线分别交AB 、BC 延长线于F 、E ，求证：⑴∠EAD =∠EDA ；⑵DF ∥AC ；⑶∠EAC =∠B ．训练1. D 为BC 中点，DE BC ⊥交BAC ∠的平分线于点E ，EF AB ⊥于F ，EG AC ⊥于G .求证：BF CG =.思维拓展训练(选讲)能力提升21ADCBA B C DE F O G ODCBAFAGEDCB训练2.已知：如图，ABC∠及两点M、N．求作：在平面内找一点P，使得PM PN=，且P点到ABC∠两边所在的直线的距离相等．NMBCA训练3.如图，在ABC△中，BD、CD分别平分ABC∠和ACB∠．DE AB FD AC∥，∥．如果6BC=，求DEF△的周长．训练4.已知：如图，在POQ∠内部有两点M、N，MOP NOQ∠=∠．⑴画图并简要说明画法：在射线OP上取一点A，使点A到点M和点N的距离和最小；在射线OQ上取一点B，使点B到点M和点N的距离和最小；⑵直接写出AM AN+与BM BN+的大小关系．知识模块一轴对称图形的认识与应用课后演练【演练1】⑴下面四个图形中，从几何图形的性质考虑，哪一个与其他三个不同？请指出这个图形，并简述你的理由．实战演练FEDCBAMNQO④③②①答：图形__________；理由是__________．⑵ 画出下图所示的轴对称图形的对称轴：⑶ 如图是奥运会会旗上的五环图标，它有（ ）条对称轴．A ．1B ．2C ．3D ．4⑷ 下列图形中，不是轴对称图形的是（ ）．A ．角B ．等边三角形C ．线段D ．不等边三角形⑸ 如图，它们都是对称的图形，请观察并指出哪些是轴对称图形，哪些图形成轴对称.【演练2】 如图，把ABC △纸片沿DE 折叠，当点A 落在四边形BCED 的外部时，则A ∠与1∠和2∠之间有一种数量关系始终保持不变，请试着找一找这个规律，你发现的规律是（ ）． A ．12A ∠=∠-∠B ．212A ∠=∠-∠C ．3212A ∠=∠-∠D ．()3212A ∠=∠-∠知识模块二 线段的垂直平分线 课后演练【演练3】 如图，已知40AOB ∠=︒，CD 为OA 的垂直平分线，求ACB ∠的度数．21E ADCBO DC BA知识模块三角平分线性质及常见辅助线模型（一）课后演练【演练4】如图，BD CD=，90ABD ACD∠=∠=°，点E、F分别在AB、AC 上，若ED平分BEF∠．①求证：FD平分EFC∠；②求证：EF BE CF=+.【演练5】证明：三角形一个内角的平分线与另外两个外角的平分线交于一点．FEDC BA。