第四章_非线性数规划

非线性规划非线性规划是一种涉及非线性目标函数和/或非线性约束条件的优化问题。

与线性规划不同，非线性规划可能存在多个局部最优解，而不是全局最优解。

非线性规划在许多领域都有广泛的应用，如经济学、工程学和管理学等。

非线性规划的一般形式可以表示为：最小化或最大化 f(x)，其中 f(x) 是一个非线性函数，x 是决策变量向量。

满足一组约束条件g(x) ≤ 0 和 h(x) = 0，其中 g(x) 和 h(x) 是非线性函数。

为了求解非线性规划问题，可以使用不同的优化算法，如梯度下降法、牛顿法和拟牛顿法等。

这些算法的目标是找到目标函数的最小值或最大值，并满足约束条件。

非线性规划的难点在于寻找全局最优解。

由于非线性函数的复杂性，这些问题通常很难解析地求解。

因此，常常使用迭代算法来逼近最优解。

非线性规划的一个重要应用是在经济学中的生产计划问题。

生产活动通常受到多个因素的限制，如生产能力、原材料和劳动力等。

非线性规划可以帮助确定最佳的生产数量，以最大化利润或最小化成本。

另一个应用是在工程学中的优化设计问题。

例如，优化某个结构的形状、尺寸和材料以满足一组要求。

非线性规划可以帮助找到最佳设计方案，以最大程度地提高性能。

在管理学中，非线性规划可以用于资源分配和风险管理问题。

例如，优化一个公司的广告预算，以最大程度地提高销售额。

非线性规划可以考虑多种因素，如广告投入和市场需求，以找到最佳的广告投放策略。

总之，非线性规划是一种重要的优化方法，用于解决涉及非线性目标函数和约束条件的问题。

它在经济学、工程学和管理学等领域有广泛的应用。

尽管非线性规划的求解难度较大，但通过合适的优化算法，可以找到最佳的解决方案。

非线性规划（nonlinear programming）1.非线性规划概念非线性规划是具有非线性约束条件或目标函数的数学规划，是运筹学的一个重要分支。

非线性规划研究一个n元实函数在一组等式或不等式的约束条件下的极值问题，且目标函数和约束条件至少有一个是未知量的非线性函数。

目标函数和约束条件都是线性函数的情形则属于线性规划。

2.非线性规划发展史公元前500年古希腊在讨论建筑美学中就已发现了长方形长与宽的最佳比例为0.618,称为黄金分割比。

其倒数至今在优选法中仍得到广泛应用。

在微积分出现以前，已有许多学者开始研究用数学方法解决最优化问题。

例如阿基米德证明：给定周长，圆所包围的面积为最大。

这就是欧洲古代城堡几乎都建成圆形的原因。

但是最优化方法真正形成为科学方法则在17世纪以后。

17世纪，I.牛顿和G.W.莱布尼茨在他们所创建的微积分中，提出求解具有多个自变量的实值函数的最大值和最小值的方法。

以后又进一步讨论具有未知函数的函数极值，从而形成变分法。

这一时期的最优化方法可以称为古典最优化方法。

最优化方法不同类型的最优化问题可以有不同的最优化方法，即使同一类型的问题也可有多种最优化方法。

反之,某些最优化方法可适用于不同类型的模型。

最优化问题的求解方法一般可以分成解析法、直接法、数值计算法和其他方法。

(1)解析法：这种方法只适用于目标函数和约束条件有明显的解析表达式的情况。

求解方法是：先求出最优的必要条件，得到一组方程或不等式，再求解这组方程或不等式，一般是用求导数的方法或变分法求出必要条件，通过必要条件将问题简化，因此也称间接法。

(2)直接法：当目标函数较为复杂或者不能用变量显函数描述时，无法用解析法求必要条件。

此时可采用直接搜索的方法经过若干次迭代搜索到最优点。

这种方法常常根据经验或通过试验得到所需结果。

对于一维搜索(单变量极值问题)，主要用消去法或多项式插值法；对于多维搜索问题(多变量极值问题)主要应用爬山法。

非线性规划什么是非线性规划？非线性规划（Nonlinear Programming，简称NLP）是一种数学优化方法，用于求解包含非线性约束条件的优化问题。

与线性规划不同，非线性规划中的目标函数和约束条件都可以是非线性的。

非线性规划的数学表达式一般来说，非线性规划可以表示为以下数学模型：minimize f(x)subject to g_i(x) <= 0, i = 1, 2, ..., mh_j(x) = 0, j = 1, 2, ..., px ∈ R^n其中，f(x)是目标函数，g_i(x)和h_j(x)分别是m个不等式约束和p个等式约束，x是优化变量，属于n维实数空间。

非线性规划的解法由于非线性规划问题比线性规划问题更为复杂，因此解决非线性规划问题的方法也更多样。

以下列举了几种常用的非线性规划求解方法：1. 数值方法数值方法是最常用的非线性规划求解方法之一。

它基于迭代的思想，通过不断优化目标函数的近似解来逼近问题的最优解。

常见的数值方法有梯度下降法、牛顿法、拟牛顿法等。

2. 优化软件优化软件是一类针对非线性规划问题开发的专用软件，它集成了各种求解算法和优化工具，可以方便地求解各种类型的非线性规划问题。

常见的优化软件有MATLAB、GAMS、AMPL等。

3. 线性化方法线性化方法是一种将非线性规划问题转化为等价的线性规划问题的求解方法。

它通过线性化目标函数和约束条件，将非线性规划问题转化为线性规划问题，然后利用线性规划的求解方法求解得到最优解。

4. 分类方法分类方法是一种将非线性规划问题分解为若干个子问题求解的方法。

它将原始的非线性规划问题分解为多个子问题，然后将每个子问题分别求解，并逐步逼近原始问题的最优解。

以上仅是非线性规划求解方法的一小部分，实际上还有很多其他的方法和技巧可供选择。

在实际应用中，选择合适的方法和工具是非常重要的。

非线性规划的应用非线性规划在实际生活和工程中有着广泛的应用。

第四章 非线性规划教学重点：凸规划及其性质，无约束最优化问题的最优性条件及最速下降法，约束最优化问题的最优性条件及简约梯度法。

教学难点：约束最优化问题的最优性条件。

教学课时：24学时主要教学环节的组织：在详细讲解各种算法的基础上，结合例题，给学生以具体的认识，再通过大量习题加以巩固，也可以应用软件包解决一些问题。

第一节 基本概念教学重点：非线性规划问题的引入，非线性方法概述。

教学难点：无。

教学课时：2学时主要教学环节的组织：通过具体问题引入非线性规划模型，在具体讲述非线性规划方法的求解难题。

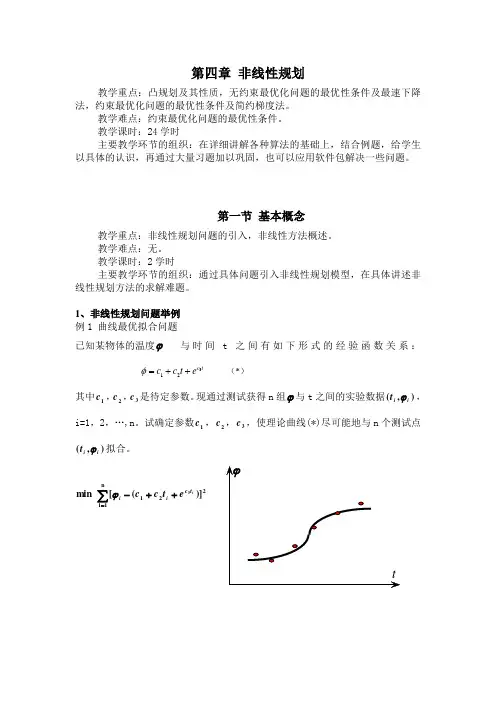
1、非线性规划问题举例例1 曲线最优拟合问题已知某物体的温度ϕ 与时间t 之间有如下形式的经验函数关系：312c t c c t e φ=++ （*）其中1c ，2c ，3c 是待定参数。

现通过测试获得n 组ϕ与t 之间的实验数据),(i i t ϕ，i=1，2，…,n 。

试确定参数1c ，2c ，3c ，使理论曲线(*)尽可能地与n 个测试点),(i i t ϕ拟合。

∑=++-n 1i 221)]([ min 3i t c i i e t c c ϕ例 2 构件容积问题通过分析我们可以得到如下的规划模型：⎪⎪⎩⎪⎪⎨⎧≥≥=++++=0,0 2 ..)3/1( max 212121222211221x x S x x x x a x x t s x x a V ππππ基本概念设n T n R x x x ∈=),...,(1，R R q j x h p i x g x f n j i :,...,1),(;,...,1),();(==,如下的数学模型称为数学规划(Mathematical Programming, MP)：⎪⎩⎪⎨⎧===≤q j x h p i x g t s x f j i ,...,1,0)( ,...,1,0)( ..)( min约束集或可行域X x ∈∀ MP 的可行解或可行点MP 中目标函数和约束函数中至少有一个不是x 的线性函数，称(MP)为非线性规划令 T p x g x g x g ))(),...,(()(1=T p x h x h x h ))(),...,(()(1=，其中，q n p n R R h R R g :,:，那么(MP )可简记为⎪⎩⎪⎨⎧≤≤ 0)( 0 ..)( min x h g(x)t s x f 或者 )(min x f X x ∈ 当p=0,q=0时，称为无约束非线性规划或者无约束最优化问题。

第二节 SUMT 方法（罚函数法）一、SUMT 方法的原理SUMT （sequential unconstrained minimization technique ）法，序列无约束极小化方法,亦称为罚函数法。

它是一种不等式约束最优化问题的间接解法 它的基本思想是将原来的目标函数和约束函数按一定的方式构成一个新的函数，在这个新函数中，既包括目标函数，又包括全部约束函数和一个可以变化的乘子。

当这个乘子按一定的方式改变时，就得到一个新函数序列，求每一个新函数的最优解都是一个无约束最优化问题，这样就把一个约束最优化问题转化为一系列无约束最优化问题进行求解。

所得到的最优解序列将逐步逼近原问题的最优解。

引例一：min()f X ax = s.t()0g X b x =-≤ 显然f （X ）的最优点为x*=b ，对应的最小值为f（X*）=ab用SUMT 求解函数的最优解构造函数 11(,)()()k k kX r f X r ax r g X b xΦ=-=-- 0k r >—可变化乘子，它是一个很小的正数。

其最优解为：*()k X r b =+此时对应的(,)k X r Φ的最小值为***1(,)k kX r ax r b x ab Φ=--=+ 最优点*()k X r 和最小值*(,)k X r Φ均是k r 的函数。

当k r 取不同值时，它们有不同的值，而当0k r →时，**()k X r X b →=，*(,)*k X r f X ab Φ→=（），即最后收敛于约束最优点。

0min lim[min (,)]() {|()0}k k i r X r f X R X g X X R→Φ==≤∈ 以上分析从理论上说明了无约束最优化问题min (,)k X r Φ与约束优化问题min () {|()0}i f X R X g X X R=≤∈之间的联系：约束非线性规划问题可以通过构造新目标函数序列，用无约束优化方法求其极小点，并逐次逼近原问题的最优点。

第二节 SUMT 方法（罚函数法）一、SUMT 方法的原理SUMT （sequential unconstrained minimization technique ）法，序列无约束极小化方法,亦称为罚函数法。

它是一种不等式约束最优化问题的间接解法 它的基本思想是将原来的目标函数和约束函数按一定的方式构成一个新的函数，在这个新函数中，既包括目标函数，又包括全部约束函数和一个可以变化的乘子。

当这个乘子按一定的方式改变时，就得到一个新函数序列，求每一个新函数的最优解都是一个无约束最优化问题，这样就把一个约束最优化问题转化为一系列无约束最优化问题进行求解。

所得到的最优解序列将逐步逼近原问题的最优解。

引例一：min ()f X ax =s.t ()0g X b x =-≤显然f （X ）的最优点为x*=b ，对应的最小值为f （X*）=ab用SUMT 求解函数的最优解 构造函数11(,)()()k k kX r f X r ax r g X b xΦ=-=-- 0k r >—可变化乘子，它是一个很小的正数。

其最优解为：*()k X r b =+ 此时对应的(,)k X r Φ的最小值为***1(,)k kX r ax r b x ab Φ=--=+最优点*()k X r 和最小值*(,)k X r Φ均是k r 的函数。

当k r 取不同值时，它们有不同的值，而当0k r →时，**()k X r X b →=，*(,)*k X r f X ab Φ→=（），即最后收敛于约束最优点。

0min lim[min (,)]() {|()0}k k i r X r f X R X g X X R→Φ==≤∈ 以上分析从理论上说明了无约束最优化问题min (,)k X r Φ与约束优化问题min () {|()0}i f X R X g X X R=≤∈之间的联系：约束非线性规划问题可以通过构造新目标函数序列，用无约束优化方法求其极小点，并逐次逼近原问题的最优点。