惠更斯菲涅尔原理基尔霍夫衍射理论

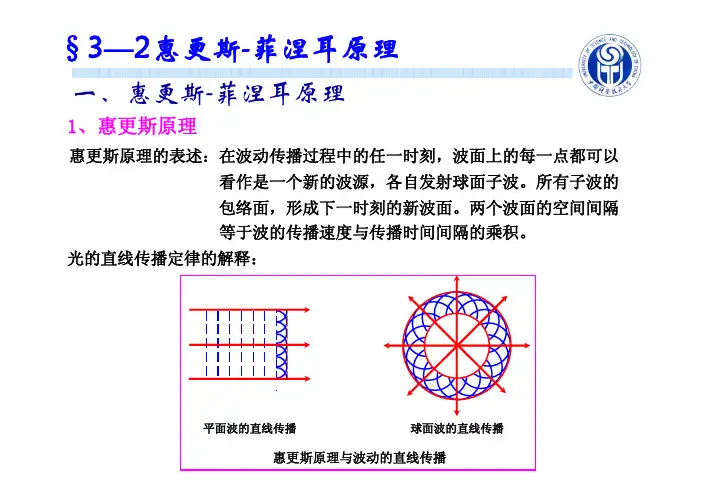
§3—2惠更斯-菲涅耳原理一、惠更斯-菲涅耳原理1、惠更斯原理惠更斯原理的表述：在波动传播过程中的任一时刻，波面上的每一点都可以 看作是一个新的波源，各自发射球面子波。

所有子波的 包络面，形成下一时刻的新波面。

两个波面的空间间隔 等于波的传播速度与传播时间间隔的乘积。

光的直线传播定律的解释：平面波的直线传播球面波的直线传播惠更斯原理与波动的直线传播衍射现象的定性解释：光波的衍射2、惠更斯-菲涅耳原理(1) 惠更斯原理的局限性没有涉及波动的时空周期特性，即波长、振幅、相位等。

虽然可以用 于确定光的传播方向，但无助于确定沿不同方向传播的光波的振幅和相位 大小。

(2) 惠更斯-菲涅耳原理菲涅耳对惠更斯原理的贡献：将不同子波的干涉叠加引入惠更斯原理，并赋予其以相应的相位和振幅表达式。

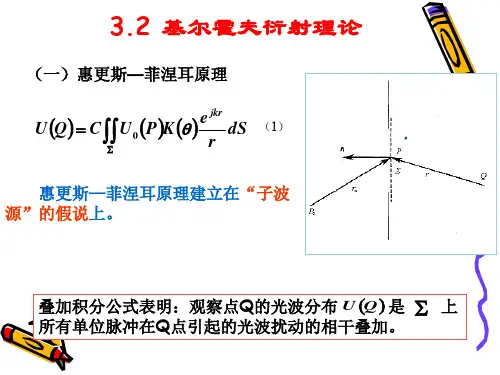
evΔS θ r P*S：t时刻波阵面 ΔS：波阵面上面元S(子波波源)ΣdΣθ0 nθSRQr惠更斯-菲涅耳原理S：光源Σ ：光源S发出的光波的任一波面dΣ ：波面Σ上位于Q点的面元Pn：面元d Σ 的法线方向单位矢量θ0：光源S到点Q连线与面元法线夹角θ：Q点到场点P的连线与面元法线夹角惠更斯-菲涅耳原理的表述：波面Σ 上的每个面元dΣ 都可以看作是新的波源，它们均发射球面子波，在与波面相距为r处的P点的光振动Ê0(P)，等于所有球面子波在该点的 光振动Ê0(P)的相干叠加：E~(P) = ∫∫ d E~(P) Σ按照菲涅耳的假设，Q点处dΣ 面元发出的球面子波在P点的光振动复振幅：dE~(P) =KF (θ0,θ)E0(Q)eikr rdΣK：比例常数；Ê0(Q)：光源S在Q点引起光振动复振幅；F(θ0, θ )：倾斜因子，随θ0和θ 的增大而减小。

P点总的光振动复振幅——菲涅耳衍射积分式：E~(P) =K ∫∫∑F(θ0,θ)E~0(Q)eikr rdΣ3、菲涅耳－基尔霍夫衍射积分基尔霍夫通过由电磁场理论严格地数学推导得到：K=−iλF(θ 0,θ)=1 2(cosθ 0+cosθ)基尔霍夫边界条件：设波面处放置一开孔的无限大不透明光屏，且开孔所对应的波面面积为Σ0，则透过光屏的光振动满足：E~0(Q)=⎨⎧E~0 ⎩0(Q)Q在Σ以内0Q在Σ以外0∫∫ 菲涅耳-基尔霍夫衍射积分：E~(P) =−iλΣ0(cosθ0 +2cosθ)E~0(Q)eikr rdΣ① 当波面为以S点为中心的球面时， θ 0=0，F(θ0, θ)=(1+cosθ )/2，只与场点P相对波面的方位有关。

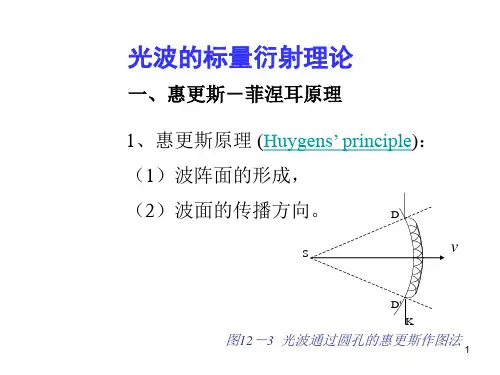
1惠更斯－菲涅尔原理⏹ 惠更斯－菲涅耳原理可以表述如下：⏹ 波前上每一个面元都可看成是新的振动中心，它们发出次波（频率与入射波相同）; ⏹ 在空间某一点P 的振动是所有这些次波在该点的相干迭加。

⏹ 是相干叠加→复振幅叠加 ⏹ 如图所示。

点光源S 在波面∑’ 上任一点Q 产生的复振幅为 ⏹ 式中，A 是离点光源单位距离处的振幅， ⏹ R 是波面∑’的半径。

⏹ 在Q 点处取面元d σ，面元发出的子波在P 点产生的复振幅与在面元上的复振幅 、面元大小和倾斜因子K(θ)成正比。

⏹ 面元d σ在P 点产生的复振幅可以表示为⏹ K(θ)表示子波的振幅随面元法线与QP 的夹角θ的变化。

（ θ称为衍射角） ⏹ c 为一常数,r=QP 。

⏹ 菲涅耳假设：当时θ=0 ，倾斜因子K 有最大值，随着增加θ↑ ，K 减小， ⏹ 当θ≥π/2时，K=0。

(基尔霍夫理论证明不正确)⏹ 对P 点产生作用的将是波面∑’中界于z z’范围内的波面∑上的面元发出的子波。

⏹ 则：⏹ 此即为惠更斯－菲涅耳原理的菲涅耳表达式，此关系式还可推广为（5－4）式， ⏹ 即⏹ 若： ⏹ 有： 2基尔霍夫衍射理论⏹ 基尔霍夫理论，只适用于标量波的衍射，故又称标量衍射理论。

3巴俾涅（Babinet ）原理 即两个互补屏单独产生的衍射场的复振幅之和等于没有屏时的复振幅。

在 的那些点，两个互补屏单独产生的强度相等。

菲涅耳衍射是普遍的，夫琅和费衍射是菲涅耳衍射的特例⏹ 基尔霍夫衍射公式的近似：⏹ 1.傍轴近似：入射光垂直孔径面 ⏹ 2.菲涅耳近似 ：S ()ikR RA E Q exp ~→= ()()()()σθd r ikr R ikR A cK P E d exp exp ~→= ()()()()⎰⎰∑=σθd rikr K R ikR A c P E exp exp ~ ()ikR RA E Q exp ~ =()()()()⎰⎰∑=σθd K rikr Q E c P E exp ~~ ()0P ~=E ()111,1z r K ≈=θ()()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡-+-+=2121211211z y y x x z r⏹ 3.夫琅和费近似：⏹ 4.菲涅耳衍射公式：⏹ 5.夫琅和费衍射公式： ⏹ 即只有在很远距离上才能观察到夫琅和费衍射条纹，在实验室中很难实现。

光的传播是光学研究的基本问题之一，也是光能够记录、存储、处理和传送信息的基础。

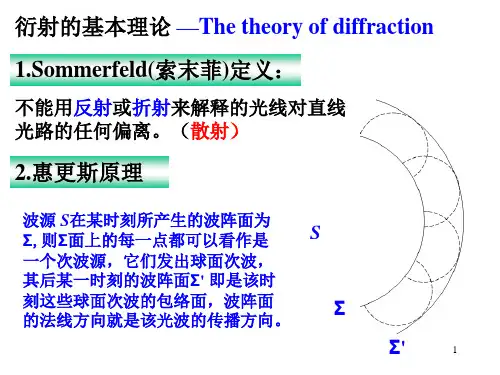
众所周知，几何光学的基本定律——光沿直线传播，是光的波动理论的近似。

作为电磁波的光的传播要用衍射理论才能准确说明。

衍射是波动传播过程的普遍属性，是光具有波动性的表现。

电磁波是矢量波，精确解决光的衍射问题，必须考虑光波的矢量性。

用矢量波处理衍射过程非常复杂，这是因为电磁场矢量的各个分量通过麦克斯韦方程联系在—起，不能单独处理；但是在光的干涉、衍射等许多现象中，只要满足：(1) 衍射孔径大于波长；(2) 观察点与衍射屏足够远。

不考虑电磁波场矢量的各矢量之间的联系，把光作为标量波处理结果与实际结果很接近，处理衍射问题变得简单。

经典的标量衍射理论最初于1678年由惠更斯提出，1818年菲涅耳引入干涉概念，补充了惠更斯理论，1882年基尔霍夫利用格林定理，导出了严格的衍射公式。

由于任意光波场可以展开为平面波的叠加，用平面波作为基元函数也可描述衍射现象，这就是研究衍射的角谱理论提出光的衍射现象，按光源、障碍物和观察平之间的关系大小分为两种：(1)菲涅尔衍射；(2)夫琅和费衍射。

衍射公式和傅里叶变换之间有着明显的相同之处，不论对于两种衍射的那一种，尽可能将衍射公式和衍射屏透过率函数的傅里叶变换联系起来，不仅使计算方便，而且直接应用傅里叶变换的性质，也会对光学信息处理带来方便。

本章将用平面波角谱理论导出同样衍射公式，说明光的传播过程作为线性系统用频率（角谱）方法在频域中分析，与用脉冲响应在空域中分析是完全等价的，进而用角谱理论方法讨论菲涅耳衍射和夫琅和费衍射。

第二章标量衍射理论本章内容2.1 惠更斯—菲涅耳原理2.2 基尔霍夫衍射理论2.3 菲涅耳衍射和夫琅和费衍射2.4 衍射的角谱理论§2.1 惠更斯—菲涅耳原理知识要点：菲涅耳处理衍射问题的思路§2.1 惠更斯—菲涅耳原理惠更斯指出：波前上每一面元都可看作一个次级波源，它们产生球面子波，后一时刻的波前位置是所有这些子波的包络面。