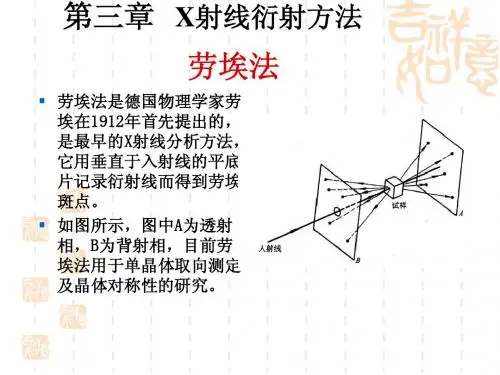
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求在z>0半空间中的光波复振幅。
如孔径是在一无穷大的不透明屏幕 上开孔,则该孔径的透射函数为
t
(
x,
y)
=
⎧1, ⎨
⎩0,
(x, y)在Σ上; 其他.
更一般的情况是,在孔径内可以有位相改变,如在孔径内有透镜、棱 镜或透明薄膜等光学元件。这时,可定义复振幅透过率来表示孔径的
透射函数,它是紧靠孔径后的平面上的出射光场复振幅与入射光场的
第三章 衍射
1. 引言 2. 平面波角谱的衍射理论 3. 菲涅尔近似与夫琅和费近似 4. 焦点附近的光场分布 5. 无衍射光束—Bessel光束
1. 引言
惠更斯原理
惠更斯首先用光的波动说来解释衍射现象。惠更斯原理把光波的 传播看成是这样一种过程:光波扰动(波前)所到达的每一点都起着一 个次级波源(子波源)的作用,每一个次级波源发出次级球面波(子 波),它向四面八方扩展,所有这些次级波的包络面便是新的波前。
因为孔径外的场为0,所以上式可以写为
∫ ∫ U (x, y, z) =
∞
2π z
−∞ dfxdf y
U
Σ
(
x0
,
y0
,
0)
exp(i
λ
1−
λ
2
f
2 x
−
λ
2
f
2 y
)
iexp{i2π[ fx (x − x0 ) + fy ( y − y0 )]}dx0dy0
以上用平面波角谱表示的衍射积分与惠更斯-菲涅尔原理的 基尔霍夫衍射积分公式是等价的。
基尔霍夫衍射积分定理
基尔霍夫理论的主要简化和近似是把光作为标量来处理,也就是 只考虑电磁场的一个横向分量的复振幅。并且假定任何别的有关分量可 以用同样的方式独立处理。而实际上电磁场矢量的各个分量是通过麦克 斯韦方程组联系在一起的,不能独立处理。研究表明,只要满足两个条 件(1)衍射孔径比波长大得多,(2)不要在太靠近孔径的地方观察衍 射场,则标量理论可以得到满意的结果。
复振幅之比,
t(x, y) = Ut (x, y, 0) , 或 Ui (x, y, 0)
Ut (x, y, 0) = Ui (x, y, 0)t(x, y),
只要找出与 Ut
相应的角谱
At
( coλs α
,
cos
λ
β
)
和与
Ui
相应的角谱
Ai
(
cosα λ
,
cos
λ
β
)
之间的关系,就解决了这个问题。
基尔霍夫衍射公式
∫ ∫ U (x, y, z) = 1
iλ
∞ −∞
∞ −∞
U
(
x0
,
y0
)
exp(ikr r
)
cosθ
dx0
dy0
.
另一种完全波集是平面波集,即任意波长可以按平面波作展开, 这就是平面波角谱方法。这种方法首先是由瑞利用于描述平面波照明时 在褶皱介质边界上的透射和反射场。德拜在1909年用这种方法研究焦点 附近的场。1902年惠泰克证明用平面波角谱所描述的场是波动方程的 解。此后,从20世纪50年代至70年代,衍射理论的这一方法在无线电传 播理论中得到了广泛的应用。
2π λ
z
1−
λ2
f
2 x
−
λ2
f
2 y
)
∫ ∫ U (x, y, z) =
∞ −∞
∞
2π z
U
−∞
(
x0
,
y0
,
0)
exp(i
λ
1−
λ
2
f
2 x
−
λ
2
f
2 y
)
iexp{i2π[ fx (x − x0 ) + fy ( y − y0 )]}dfxdfydx0dy0
这是平面波角谱衍射理论的基本公式。
2. 平面波角谱的衍射理论
衍射孔径对角谱的效应
一个严格的单色平面波在时间和空间上应是无限的。如果一个平 面波入射到一个孔径上,即被该孔径所限制,显然这时由孔径出射的场 就不再是一个准确的平面波了。这就是我们要研究的衍射孔径对角谱的 扰动效应。
已知z=0平面处有一孔径,入射到该孔径上的复振幅为 Ui (x, y, 0),
由傅立叶变换定理可得
At
( coλs α
,
cos
λ
β
)
=
Ai
(
cosα λ,ຫໍສະໝຸດ cosλβ
)
*T
(
cosα λ
,
cos
λ
β
)
T (cosα , cos β ) λλ
为孔径函数的傅立叶变换。
卷积运算具有展宽带宽的性质。由于透射波的角谱等于入射波的
角谱与孔径函数的傅立叶变换的卷积,因此引入使入射波在空间上受限
制的衍射孔径的效应就是展宽了光波的角谱。而不同的角谱分量相应于
不同方向传播的平面波分量,故角谱的展宽就是在透射波中除了包含于
入射波相同方向传播的分量之外,还增加了一些与入射波传播方向不同
的平面波分量,即增加了一些高空间频率的波,这就是衍射波。
平面波角谱的衍射理论
如果在 z = 0 处有一孔径,则 U (x, y, 0) 为通过孔径后的透射光场。
惠更斯-菲涅尔原理
惠更斯可以用来确定波的传播方向,但不能解释衍射条纹的出 现,不能给出衍射光电场的定量分布。
菲涅尔综合惠更斯原理和干涉原理,认为次级波源是彼此相干 的,由此得到惠更斯-菲涅尔原理:波前上任何一个未受阻挡的点, 都可以看作为一个次级波源,在其后空间任一点P处的光振动,是这 些次级波源产生的次级波相干叠加的结果。
E1(P) = E0 (P)[1− exp(iπ p)],
式中 E0 (P) 为不存在屏时位于
轴上的点光源在P点引起光扰动的复振幅。
具有相同直径的不透光圆屏在P点引起的场振幅? 由巴比涅原理,有圆屏时的场为
E2 (P) = E0 (P) − E1(P) = E0 (P) exp(iπ p),
则圆屏轴上该点的光强度为
I2 (P) = E2 (P) 2 = I0 (P).
泊松点
3. 菲涅尔近似与夫琅和费近似
菲涅尔近似
考虑无穷大的不透明屏幕上 的一个有限孔径对单色光的衍 射,如图所示。
设屏的平面上的直角坐标系为
衍射要讨论的问题是,已知在 z = 0 处的光场 U (x, y, 0), 求z>0处
的光场分布 U (x, y, z).
∫ A0 ( fx , fy ) =
∞
U
−∞
(
x0
,
y0, 0) exp[−i2π (
fx x0
+
fy
y0 )]dx0dy0
A(
fx,
fy,
z)
=
A0 (
fx,
fy
) exp(i
巴比涅原理
关于互补屏衍射光分布的关系。
互补屏是指这样两个屏,其中一个的开孔部分正好对应另一个的不 透明部分。
对于上述互补屏,可得
E1(P) + E2 (P) = E0 (P) E1(P), E2 (P) 为由两个互补屏分别在P点的振幅。 E0 (P) 是没有屏时的振幅。
这个结论称为巴比涅原理。
在屏上开一圆孔时在轴上一点P 处的振幅为