5基尔霍夫衍射理论

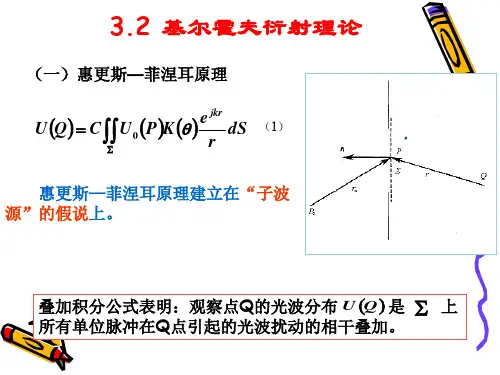
光波的传播过程就是光波衍射过程假设与近似(1)整个光波场内光矢量振动方向不变,或只考虑光矢量的一个分量;(2)衍射屏的最小尺度远大于波长.(3)观测距离远大于波长．光波衍射的线性系统分析基尔霍夫波衍射理论(书2.1惠更斯－菲涅耳原理与基尔霍夫衍射理论一、惠更斯－菲涅耳原理子波(次波)相干叠加0exp()(,)jkr K r θθdU (Q )0)jkr Σ••QrΣnθθS 1S 20exp()1(cos 2jkr r θi是在无限大不透光屏上有一开孔的情况下推导出的. 但可以推广到其它任何复杂的衍射屏。

只是此时，公式中:()()()i P U P t P =入射到衍射屏上的光场的复振幅分布，衍射屏的复振幅透过率。

光波衍射过程是线性系统变换基尔霍夫衍射积分公式为:1e (x )p j krjkr j r 1exp()1(cos 2λ=i 此式是一个叠加积分，满足线性系统的叠加性和均匀性。

因此衍射过程（光波从衍射平面到观察平面的传播过程）可以看作是一个线性系统。

是该线性系统的脉冲响应(点扩散函数可以看作是: 衍射屏上P 点的一个单位脉冲在场产生的复振幅分布。

它描述了衍射系统的特性。

相干光场在自由空间传播的平移不变性2z距z 足够大），且观察范围较0cos 1θ≈(U x 0r Si(x 0这表明，在满足一定条件下，衍射屏上各次波源在场点处所产生的复振幅分布具有相同的分布形式，只是发生了也就是说，具有平移不变性。

可写成卷积形式：21exp jk z zλ⎡+⎣0)(,)y h x x y y −−相干光场在自由空间传播的脉冲响应的近似表达式21exp jk z j zλ⎡⎣220)()1y y z ⎡+−=⎢⎣一、菲涅耳近似(傍轴近似) →菲涅耳衍射在衍射屏和观察范围确定后，当项以后的高次项，不会引起明显的相位误差。

高次项中，起主要作用的是第3项，即当由第20()(28x x zπλ⎡−+⎣201()(8x x λ⎡−+⎣exp()exp jkz jk j z λ⎡=⎢⎣系统的脉冲响应可表示为：菲涅耳衍射的脉冲响应，仍具有平移不变性0002(,)exp exp()exp 2U x y jk jkz x jk j z z λ∞−∞⎡⎢⎣⎡+⎢⎣∫二、夫琅禾费近似（远场近似）→在菲涅耳近似的基础上，如果z 进一步增大，且进一步限定衍射屏透光区域，以至于：2max 2π 可以忽略，忽略该项所引起的相位误差很小22)y y x ⎤−exp())exp jkz x jk j z λ⎛=⎜⎝22exp 2(2y x j x z z πλ⎞+⎡−⎟⎢⎣⎠000)(,;,)y h x y x y dx 则衍射的光场分布为:从上式可以看出：夫琅禾费衍射仍是线性系统，但不是平移不变系统，不再具有平移不变性。

菲涅尔基尔霍夫衍射积分公式下载温馨提示：该文档是我店铺精心编制而成，希望大家下载以后，能够帮助大家解决实际的问题。

文档下载后可定制随意修改，请根据实际需要进行相应的调整和使用，谢谢!本店铺为大家提供各种各样类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，如想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by the editor. I hope that after you download them, they can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, our shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!是描述波前衍射的一种重要数学公式，它在光学领域有着广泛的应用。

基尔霍夫方程物理化学基尔霍夫方程是物理化学中非常重要的一个概念，它描述了电路中电流的分布规律。

本文将从人类的视角出发，用通俗易懂的语言，向读者介绍基尔霍夫方程的概念和应用。

第一段：引言基尔霍夫方程是物理化学中电路分析的基础，它能够帮助我们理解电流在电路中的流动规律。

无论是日常生活还是科学研究，电路都无处不在，因此了解基尔霍夫方程的原理和应用对我们来说是非常重要的。

第二段：基尔霍夫方程的概念基尔霍夫方程由德国物理学家基尔霍夫在19世纪提出，它是根据电流守恒和电荷守恒定律推导得出的。

基尔霍夫方程主要包括两个基本原理：电流守恒和电势守恒。

电流守恒原理表明，在一个节点处，进入和离开节点的电流之和为零；电势守恒原理则要求在一个回路中，电路中各个点的电势差之和为零。

第三段：基尔霍夫方程的应用基尔霍夫方程的应用非常广泛，几乎涵盖了电路中所有的分析问题。

通过运用基尔霍夫方程，我们可以计算电路中各个元件的电流和电势差，从而帮助我们理解电路的工作原理。

例如，在串联电路中，我们可以利用基尔霍夫方程计算电阻上的电流，从而了解电路中各个元件的能量分配情况。

在并联电路中，基尔霍夫方程可以帮助我们计算总电流和各个支路的电流。

第四段：基尔霍夫方程的意义和应用领域基尔霍夫方程的应用不仅限于电路分析，还可以在其他领域中发挥重要作用。

例如，在化学反应中，我们可以将反应过程看作一个电路，利用基尔霍夫方程来分析反应物和生成物之间的转化关系。

在光学领域，基尔霍夫方程可以帮助我们理解光的传播规律和干涉现象。

因此，掌握基尔霍夫方程不仅有助于我们在物理化学领域的学习和研究，也可以应用于其他科学领域。

结尾段：总结基尔霍夫方程作为物理化学中的重要概念，可以帮助我们理解电路中电流的分布规律。

通过应用基尔霍夫方程，我们可以计算电路中各个元件的电流和电势差，从而帮助我们分析电路的工作原理。

此外，基尔霍夫方程还可以在化学、光学等领域中发挥重要作用。

因此，学习和掌握基尔霍夫方程对我们来说是非常有益的。

基尔霍夫定律基础知识基尔霍夫定律基尔霍夫定律是德国物理学家基尔霍夫提出的。

它既可以用于直流电路的分析，也可以用于交流电路的分析，还可以用于含有电子元件的非线性电路的分析。

运用基尔霍夫定律进行电路分析时，仅与电路的连接方式有关，而与构成该电路的元器件具有什么样的性质无关。

基尔霍夫定律是电路理论中最基本也是最重要的定律之一。

它概括了电路中电流和电压分别遵循的基本规律。

它包括基尔霍夫电流定律（KCL）和基尔霍夫电压定律（KVL）。

基尔霍夫定律是求解复杂电路的电学基本定律。

从19世纪40年代，由于电气技术发展的十分迅速，电路变得愈来愈复杂。

某些电路呈现出网络形状，并且网络中还存在一些由3条或3条以上支路形成的交点(节点)。

这种复杂电路不是串、并联电路的公式所能解决的，刚从德国哥尼斯堡大学毕业，年仅21岁的基尔霍夫在他的第1篇论文中提出了适用于这种网络状电路计算的两个定律，即著名的基尔霍夫定律。

该定律能够迅速地求解任何复杂电路，从而成功地解决了这个阻碍电气技术发展的难题。

基尔霍夫定律建立在电荷守恒定律、欧姆定律及电压环路定理的基础之上，在稳恒电流条件下严格成立。

当基尔霍夫第一、第二方程组联合使用时，可正确迅速地计算出电路中各支路的电流值。

由于似稳电流(低频交流电)具有的电磁波长远大于电路的尺度，所以它在电路中每一瞬间的电流与电压均能在足够好的程度上满足基尔霍夫定律。

因此，基尔霍夫定律的应用范围亦可扩展到交流电路之中。

基本概念：1、支路：（1）每个元件就是一条支路（2）串联的元件我们视它为一条支路（3）流入等于流出的电流的支路。

2、节点：（1）支路与支路的连接点（2）两条以上的支路的连接点（3）广义节点（任意闭合面）。

3、回路：（1）闭合的支路（2）闭合节点的集合。

4、网孔：（1）其内部不包含任何支路的回路（2）网孔一定是回路，但回路不一定是网孔。

主要内容：基尔霍夫第一定律第一定律又称基尔霍夫电流定律，简记为KCL，是电流的连续性在集总参数电路上的体现，其物理背景是电荷守恒公理。