3.2 基尔霍夫衍射理论
- 格式:ppt
- 大小:342.50 KB
- 文档页数:16


光波的传播过程就是光波衍射过程假设与近似(1)整个光波场内光矢量振动方向不变,或只考虑光矢量的一个分量;(2)衍射屏的最小尺度远大于波长.(3)观测距离远大于波长.光波衍射的线性系统分析基尔霍夫波衍射理论(书2.1惠更斯-菲涅耳原理与基尔霍夫衍射理论一、惠更斯-菲涅耳原理子波(次波)相干叠加0exp()(,)jkr K r θθdU (Q )0)jkr Σ••QrΣnθθS 1S 20exp()1(cos 2jkr r θi是在无限大不透光屏上有一开孔的情况下推导出的. 但可以推广到其它任何复杂的衍射屏。
只是此时,公式中:()()()i P U P t P =入射到衍射屏上的光场的复振幅分布,衍射屏的复振幅透过率。
光波衍射过程是线性系统变换基尔霍夫衍射积分公式为:1e (x )p j krjkr j r 1exp()1(cos 2λ=i 此式是一个叠加积分,满足线性系统的叠加性和均匀性。
因此衍射过程(光波从衍射平面到观察平面的传播过程)可以看作是一个线性系统。
是该线性系统的脉冲响应(点扩散函数可以看作是: 衍射屏上P 点的一个单位脉冲在场产生的复振幅分布。
它描述了衍射系统的特性。
相干光场在自由空间传播的平移不变性2z距z 足够大),且观察范围较0cos 1θ≈(U x 0r Si(x 0这表明,在满足一定条件下,衍射屏上各次波源在场点处所产生的复振幅分布具有相同的分布形式,只是发生了也就是说,具有平移不变性。
可写成卷积形式:21exp jk z zλ⎡+⎣0)(,)y h x x y y −−相干光场在自由空间传播的脉冲响应的近似表达式21exp jk z j zλ⎡⎣220)()1y y z ⎡+−=⎢⎣一、菲涅耳近似(傍轴近似) →菲涅耳衍射在衍射屏和观察范围确定后,当项以后的高次项,不会引起明显的相位误差。
高次项中,起主要作用的是第3项,即当由第20()(28x x zπλ⎡−+⎣201()(8x x λ⎡−+⎣exp()exp jkz jk j z λ⎡=⎢⎣系统的脉冲响应可表示为:菲涅耳衍射的脉冲响应,仍具有平移不变性0002(,)exp exp()exp 2U x y jk jkz x jk j z z λ∞−∞⎡⎢⎣⎡+⎢⎣∫二、夫琅禾费近似(远场近似)→在菲涅耳近似的基础上,如果z 进一步增大,且进一步限定衍射屏透光区域,以至于:2max 2π 可以忽略,忽略该项所引起的相位误差很小22)y y x ⎤−exp())exp jkz x jk j z λ⎛=⎜⎝22exp 2(2y x j x z z πλ⎞+⎡−⎟⎢⎣⎠000)(,;,)y h x y x y dx 则衍射的光场分布为:从上式可以看出:夫琅禾费衍射仍是线性系统,但不是平移不变系统,不再具有平移不变性。
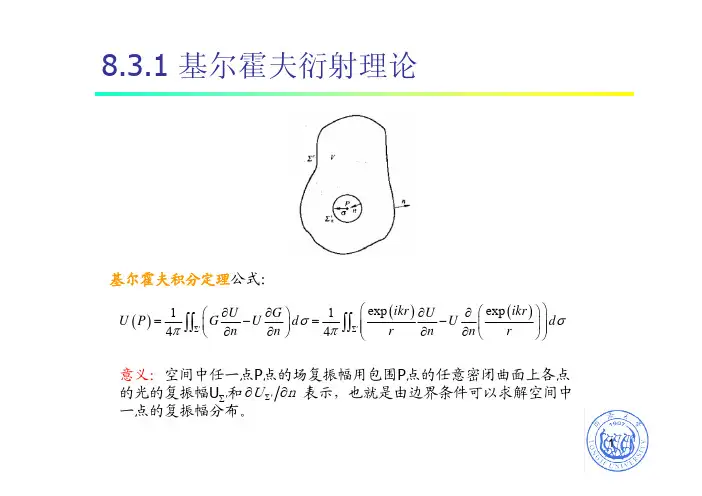
13.()exp⎞⎞ikr值由入射波决定,与不存在不透明屏时完全相同;23r′4r′5r′根据二项式展开公式同济大学物理系6789)=-0.5同济大学物理系10指向负方向。
()()()F w C w iS w =+⎞⎟⎠dt A(w=w 2⎤−ik B(w=w 2)()11⎥y y dy 同济大学物理系1112由此得到半平面屏的菲涅耳衍射图样振幅分布:()()()12,1λ∞⎡⎤⎛⎞=−−∞⎢⎥⎜⎟⎜⎟+⎢⎥⎝⎠⎣⎦U U x y F x F i z ST OBA同济大学物理系13维分布状焦点附近的三维光分布状态没有像差的透镜,由于系统孔径光阑的限制,会聚球面波受到孔径的衍射限制而形成夫琅禾费衍射,理想的点像在透镜焦平面上形成爱里斑。
如何分析在焦平面附近的光分布情况,即三维的光强分布!•用洛德尔函数计算衍射积分(P点的复振幅U(P))在焦平面附近的任一点的光场复振幅分布就可以用德拜积分公式来表示,此积分公式把场表示成不同传播方向的平面波的叠加。
同济大学物理系14焦点附近的三维光分布状态维分布状Array1516r r17焦点附近的三维光分布状态维分布状()(4)ikq RiU P A ed λ−Ω=−Ω∫∫rr 德拜积分的说明:18(5)令:()cos ,cos ,a y r ηρθψ⎬==⎭θ、ψ分别为Q 点和P 点相对于OY≤≤轴的方位角。
0≤ρ≤1P(x,y,z)ÆP(r*sin ψ, r*cos ψ, z)Q(ξ,η,ζ)ÆQ(a ρ*sin θ, a ρ*cos θ, ζ)Q 点是球面W 上一点,则有:19202π⎛⎞2a Array21⎝⎠⎣⎦=−200()(11)U P e ed d fρρθλ∫∫上式中对θ的积分可利用贝塞尔恒等式:21πθ()()00exp cos 2J x jx d θψπ=−−⎡⎤⎣⎦∫代入到德拜积分式:()22121222()f i u iu a ia AU P e J v ed fρπρρρλ⎛⎞−⎜⎟⎝⎠=−∫把实部和虚部积分分开:2112iu ρ−=−()()()02,,J v ed C u v iS u v ρρρ∫22232411cos sinu u Array25()1J x Array26三维的强度分布:I ⎤⎞⎪⎬⎥⎟27⎠⎪⎦⎭2+n sv=0)28维分布状焦点附近的三维光分布状态图:圆孔衍射会聚球面波子午面上焦点附近的等照度线。

第三章:标量衍射理论基础历史引言 数学预备知识 平面屏幕衍射的基尔霍夫理论 平面屏幕衍射的瑞利-索末非理论 瑞利-索末非理论推广到非单色波情形 在边界上的衍射 平面波的角谱1:历史引言光的波动理论形成 *惠更斯原理 *惠更斯——菲涅尔原理ndΣ QSΣ(波前)·θ r% dU ( p ) • p% U ( p) =% dU ( p ) ∫∫衍射:不能用反射或折射来解释的光线对直线光路的偏离现像— Sommerfield标量衍射理论(傅立叶光学\信息光学,波动光学,近场光学,激光光学)只考虑电场或磁场的一个横分量的标量振幅和行为,而 假定任何别的有关分量也具有相同的行为,可以用同样 的方式来独立处理。
电场 \ 磁场 的各个分量通过麦氏方程耦合起来 , 并不能独 立的处理。
标量衍射理论的适用性和局限性 1、衍射孔径∑>λ 2、不要在太靠近孔径的地方观察衍射场 (傍轴条件) 比如:高分辨率光栅,使用标量衍射理论有其很 大的局限性 f=1/d,d越小越精细,则空间频率越高,场甚至 不能以辐射波的形式传播,以表面波的形式存在。
衍射理论的种类 1)惠-菲衍射理论 2)基尓霍夫衍射理论 3)瑞-索衍射理论 4)角谱衍射理论 5)边界衍射理论HF衍射理论v nv r21Q θdΣθ0% U ( p) =% dU ( p ) ∫∫ikr01v r01ΣSikr21% dU ( p ) •pikr01Ae % ( p ) = U (Q ) F (θ , θ ) e % dU dΣ = 0 r01 r21e F (θ 0 , θ ) dΣ r01ikr01% ( p ) = Ae U r21ikr21e ∫∫ F (θ 0 , θ ) r01 d Σ惠-菲原理的数学表达式2:数学预备知识2.1.单色平面波表示法和亥姆霍兹Helmholtz方程单色波(实数)U ( P,t ) = U ( P ) cos[2πν t + ϕ ( p )]单色波的复数表示% Re[U ( P )e − i 2πν t ]% U ( P ) = U ( P )e − iϕ ( p ) → 复振幅U ( P ) → 实振幅U ( P, t )满足标量波动方程1 ∂2 ∇ U ( P, t ) − 2 2 U ( P, t ) = 0 c ∂t2% U ( P)满足不含时的helmholtz方程% ( ∇ 2 + k 2 )U ( P ) = 0自由空间传播的任何单色光扰动的复振幅必满足H.E.2.2 格林定理衍射、传播→不见源只见面→表-里⇒高斯定理→格林定理定义:令U(P)和G(P)为位置坐标的两个任意的复值函数,S为包围体积 定义 V的封闭曲面,若U、G以及它们的一阶和二阶偏微商都是单值的并 且在S内和S上连续,则有:∂U ∂G ∫ V ∫ (G∇ U − U ∇ G)dv = ∫ ∫ (G ∂n − U ∂n )ds ∫ S2 2∂ 表示在S上每一点沿向外的法线方向上的偏微商。

基尔霍夫衍射公式推导基尔霍夫衍射公式推导引言:基尔霍夫衍射公式是现代光学学科的重要组成部分之一,而作为学术领域中的高深理论,公式的具体推导过程也十分的繁琐,需要阅读者具有一定的专业知识和数学功底。
本文旨在为读者介绍基尔霍夫衍射公式的具体推导过程,帮助读者更好地掌握该重要理论。
一、基尔霍夫衍射公式的定义基尔霍夫衍射公式是描述光在遇到三维于多维不规则物体时的衍射特性的一种数学模型。
其一般形式为:U(P) = (1 / (2π)) ∫∫ U(Q) (k² - k´²) exp[-i(k - k´) · r] dq其中,U(P) 为入射光波到达光屏时,光波在位置 P 上的复振幅;U(Q) 为光源面元 Q 在某个方向上发出的光波复振幅;k 和 k´分别为反射或者折射光波的波矢量;r 表示观察点 P 到源点 Q 的矢量差。
二、基尔霍夫衍射公式的推导1. 洛仑兹方程推导在光电物理学中,洛仑兹方程是描述光在一个光学介质中传播的一般方程。
在推导基尔霍夫衍射公式时,洛仑兹方程的三维形式可以写成:∇²E + k²E = 0其中 E 表示光场复振幅,k 为光波波数。
这个方程是表征波动性的基本方程,可以用来研究平面波、球面波、柱面波等不同形式的波。
2. 泊松方程推导由于洛仑兹方程中的E 是一个向量场,因此可以对其进行分量化处理。
一般地,将 E 表示为 E = (E_x, E_y, E_z),从而得到泊松方程的三维形式:∇²E_x + k²E_x = 0∇²E_y + k²E_y = 0∇²E_z + k²E_z = 0其中,k² = n²k²₀,k₀是真空中的波矢量,n 是介质的折射率。
这个方程是推导基尔霍夫衍射公式的基础。
3. 基尔霍夫-菲涅耳原理推导基尔霍夫-菲涅耳原理是描述波动的干涉与衍射现象的重要定理之一。





基尔霍夫衍射公式推导基尔霍夫衍射公式是描述光通过一个狭缝缝隙后在远处屏幕上的衍射图样的公式。
我们可以用哈密顿原理把光的传播过程写成变分形式,然后对其进行泊松求和,最终得到基尔霍夫衍射公式。
设光源位置向量为$\mathbf{r}_0$,观察屏位置向量为$\mathbf{r}$,狭缝为在$y$轴方向,宽度为$b(x)$。
则以$\mathbf{r}$为观察点时,光场可以表示为:$$E(\mathbf{r})=\frac{1}{i\lambda}\int_S E(\mathbf{r}_0) e^{i\frac{2\pi}{\lambda}\rho}dydz$$其中$\rho$为从光源点到观察点的距离,即:$$\rho=\sqrt{(x'-x)^2+y^2+z^2}$$$x'$为狭缝位置。
对$b(x)$作傅里叶变换,即:$$b(m)=\int_{-\infty}^{\infty} b(x)e^{-i2\pimx/\lambda}dx$$则$E(\mathbf{r})$可改写为:$$E(\mathbf{r})=\frac{1}{i\lambda}\int_{-\infty}^{\infty}b(m) \int_S E(\mathbf{r}_0)e^{i\frac{2\pi}{\lambda}(\rho-mx)}dydzdm$$进一步将狭缝的宽度$b(x)$拆分为$N$个小区间,每个小区间的宽度为$\delta x$,则$b(x)$可以写成:$$b(x)=\sum_{n=0}^{N-1}b_n rect\left(\frac{x-x_n}{\delta x}\right)$$其中$b_n$为第$n$个小区间的权重,$rect(x)$表示矩形函数。
将$b(x)$代入前面的公式中,得到:$$E(\mathbf{r})=\frac{\delta x}{i\lambda}\sum_{n=0}^{N-1}b_n\int_{-\infty}^{\infty} \int_S E(\mathbf{r}_0)e^{i\frac{2\pi}{\lambda}(\rho-mx_n)}rect\left(\frac{x-x_n}{\delta x}\right)dydzdm$$上式可以看做是$N$个成像问题的相干叠加。