当前位置：文档之家 › 固体物理 第一章(1)

固体物理 第一章(1)

  • 格式：ppt
  • 大小：2.89 MB
  • 文档页数：67

下载文档原格式

  / 67

合集下载

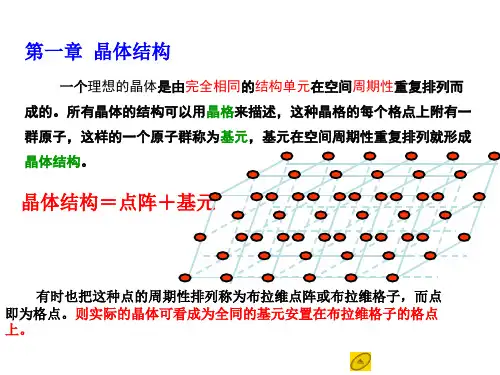
固体物理_第一章（1.4晶向、晶面指数）

固体物理_第一章（1.4晶向、晶面指数）

固体物理_第⼀章（1.4晶向、晶⾯指数）第1章晶体结构1.1 晶格的周期性1.2 典型晶格实例1.3 晶格的对称性1.4 晶向、晶⾯指数1.5 倒格⼦、布⾥渊区和晶体散射1.4.1 晶列指数（晶胞中）特别性质：所有平⾏晶列组成晶列族，包含所有格点晶列上的格点也是周期性的，且每⼀列格点分布⼀致同⼀个截⾯内，晶列是平⾏等距的晶列：连接任意格点的平⾏直线晶向：晶列的取向晶列指数：晶向的⽮量表达1.4.2 晶⾯指数（密勒指数）*平⾏的晶⾯组成晶⾯族，晶⾯族包含所有格点；* 晶⾯上的格点分布具有特定周期性，是⼆维格⼦* 同⼀族晶⾯中，每⼀个晶⾯的格点分布⼀致* 同⼀族晶⾯中，相邻晶⾯平⾏等距：系列平⾏等距晶⾯构成晶族晶⾯：晶格中任意三个不在同⼀直线上的格点决定的平⾯向与晶⾯正交（即为该晶⾯的法向⽮量）：⽤平⾯的法线式⽅程可证明若截距为负数，则对应指数头上加“-”号等效晶⾯常⽤⼤括号表⽰{hkl}，例如(100)，(010)统⼀⽤{100}表⽰，同样包括{110}、{111}晶⾯；晶⾯指数较⼩的⾯，⼀般为解理⾯晶⾯指数可⽤于计算两个⾯之间的夹⾓等效于法线⽮量的夹⾓：⼆者内积/模的乘积晶⾯指数可⽤于计算两个⾯之间的间距：等效于离原点最近的晶⾯上任意⼀点的格⽮长度，在法线⽅向的投影即，假设基⽮长度分别为a、b、c，晶⾯指数为(h, k, l)，则对应⽴体坐标系下的截距分别为a/h, b/k, c/l，继⽽，该晶⾯的法线⽮量为(h/a, k/b, l/c)，写成⽅向向量为(h/a, k/b, l/c)222选择在a轴上的截距，在法线的投影，即a/h在⽅向的投影d222。

《固体物理学》房晓勇主编教材-习题解答参考01第一章 晶体的结构

《固体物理学》房晓勇主编教材-习题解答参考01第一章 晶体的结构

(h
2 1
2 + k + l12 ) i( h22 + k22 + l2 ) 2 1 12
h1h2 + k1k2 + l1l2
12
பைடு நூலகம்
解：三个晶轴相互垂直且等于晶格常数 a，则晶胞基矢为
a1 = ai, a2 = a j, a3 = ak ,
其倒格子基矢为
b1 =
2π 2π 2π i, b2 = i, b3 = i a a a 2π ( hi + k j + lk ) a
a 2 +j a 0 − 2
a 2
a 2 +k a 0 2
0 a 2
=−
b 1=
a2 a2 a2 i+ j+ k 4 4 4
2π 2π a 2 ⎛ a 2 a2 a2 a 2 × a3 = 3 − i + j + ⎜ a Ω 2 ⎝ 4 4 4 4 2π 2π b 2= i − j + k ,b 3= i+ j−k a a
i = −( h + k )
得证 （2）由上可知，h，k，i 不是独立的， ( 001) , 133 , 110 , 323 , (100 ) , ( 010 ) , 213 . 中各 i 等于
( )( )( )
( )
i1 = −(h1 + k1 ) = −(0 + 0) = 0, i2 = 2 ， i3 = 0 ， i4 = 1 ， i5 = 1 i6 = 1 ， i7 = 3 即得
a1 ⋅ n = h1d , a2 ⋅ nh2 d , a3 ⋅ n = h3d ,
假定 h1 , h2 , h3 不是互质的数，则有公约数 p，且 p>1；设 k1 , k2 , k3 为互质的三个数，满足

固体物理第一章1

固体物理第一章1

晶格物理性质周期性（平移对称性）：
Γ (x+na) = Γ (x)
上式表示原胞中任一处x的物理性质，同另一原胞相应处的物 理性质相同。
原子
一维的喇菲格子
例：一维复式格子
定义：晶格中含有n(n≥2)类原子，其周围情况不一样，它们组成一维无
限周期性点列，周期为a。 原胞：长为a的一根直线段，一类原子在其两端点，其余原子在线段上。 每个原胞含n个原子。 周期性： Γ (x+na) = Γ (x)
晶体分单晶体和多晶体
单晶体( Single Crystal ) 原子排列的周期性是在整个固体内部存在的；无限大的严格的单 晶体可以看成是完美晶体。 多晶体( Multiple Crystal ) 由很多不同取向的单晶体的晶粒组成的固体；仅在各晶粒内原子 才有序排列，不同晶粒内的原子排列是不同的。
单晶体是个凸多面体，围成这个凸多面体的面是光滑的，称 为晶面。 晶面的大小和形状受晶体生长条件的影响，它们不是晶体品 种的特征因素。
1 a 1 ( a b c ) 2 1 a 2 (a b c ) 2 1 a 3 (a b c ) 2


a a1 ( i j k) 2 a a 2 (i - j k) 2 a a 3 (i j k) 2
四、各向异性
晶带：单晶体的晶面排列成带状，晶面的交线（称为晶棱）互相平行， 这些晶面的组合称为晶带。晶棱的方向称为带轴。 晶轴：重要的带轴，互相平行的晶棱（晶面的交线）的共同方向。
各向异性： 晶体的物理性质，常随方向不同而有量的 差异，晶体所具有的这种性质——各向异性。
如介电常数、压电常数、弹性常数等。

固体物理第1.参考答案与解析

固体物理第1.参考答案与解析

第一章 参考答案1体心立方格子和面心立方格子互为正倒格子，试证明之。

证：体心立方格子的固体物理学原胞（Primitive cell ）的三个基矢是)(2),(2),(2321→→→→→→→→→→→→-+=+-=++-=k j i a a k j i a a k j i a a ⎪⎪⎪⎭⎪⎪⎪⎬⎫+=+=+==⨯⋅=ΩΩ⨯=Ω⨯=Ω⨯=→→→→→→→→→→→→→→→→→→→→→)(2)(2)(22122,2:3213321213132321j i a b i k a b k j ab aa a a a ab a a b a a b ππππππ定义它们是倒点阵面心立方的三个基矢。

2 对六角密堆积结构固体物理学原胞基矢如→→→→→→→→=+-=+=kc a ja i a a j a i a a 321232232求倒格子基矢。

解：;,213→→→⊥a a a→→→→→→→→+-=+===ja i a a ja i a a a a a 2322322121)33(32)32(22332123213→→→→→→→→→→→→+=+Ω=Ω⨯==⨯⋅=Ω=j i aac a i ac j a a b ca aa a a kc a πππ ⎪⎭⎫ ⎝⎛+-=Ω⎪⎭⎫ ⎝⎛⨯=→→→→→j i a a a b 3332/2132ππ→→→→=Ω⎪⎭⎫⎝⎛⨯=kc a a b ππ2/22133求解简单立方中晶面指数为(hkl)的晶面簇间距。

解：正格子基矢是 →→→→→→===k a c j a b i a a ,,令 为相应的倒基矢→→→***,,c b a21222***,,3***)()()(2222)(222-→→→→→→→→→→→→→→→→→⎥⎦⎤⎢⎣⎡++==++=++==⨯⋅=Ω===a l a k ahK d kl a j k a i h a c l b k a h K a c b a kac j ab i aa hklnkl l k h πππππππ4 试证明六角密集结构中c/a=如图所示，ABC 分别表示六角密排结构中三个原子，D 表示中心的原子。

固体物理-第一章

固体物理-第一章
B A
B
C
(3)金刚石晶格
金刚石和石墨 金刚石由碳原子构成，在一个面心立方 原胞内还有四个原子，这四个原子分别 位于四个空间对角线的 1／4处。一个碳 原子和其它四个碳原子构成一个正四面 体。
金刚石晶格
c
c
金刚石晶格是由两个面心晶格重叠相嵌而成。两个面心立方 子晶格沿体对角线位移1/4的长度套构而成,
ak
a1
aj
a2 a3
ai
典型的晶体结构
结构型 单胞中的 原子在单胞 最近邻 原子个数 中的位置 距离 配位数
(Cu)
fcc
4 2
Cs+ 1
bcc
11 ( (000) 0) 22 1 1 ( 0 ) (0 1 1 ) 2 2 22
2a 2 3a 2 3a 2
12
(W)
(000)
11 1 ( ) 22 2
§1.1
一些晶格的实例
一、晶格（晶体的格子）中原子排列的具体形式。
（1）考虑原子球层的正方排列形成的晶格结构
原子正方排列: 把原子看成原子球，一层层排列，一个原子与相邻原 子组成正方形，每层都为正方排列.
如此堆积而成的晶格分为两类：
（i） 简单立方晶格
原子球规则排列最简单的形式为正方排列，如果把这样的原子层叠起来，各层的 球完全对应，上下对称，为简单立方晶格。
(1 ,2 ,3 )为一组整数
对于金刚石晶格，面心立方顶点位置的原子的位置：
1 a1 2 a 2 3 a 3
面心立方体对角线1/4处位置的原子位置： 1 a1 2 a 2 3 a 3 r 一组 1 a1 2 a 2 3 a 3 可以包括所有的格点 布拉伐格子： 由 1 a1 2 a 2 3 a 3 确定的空间格子 任一点的位矢 r，V(r ) V(r 1 a1 2 a 2 3 a 3 )，

固体物理第一章课件

固体物理第一章课件

1
3
E = V ∫0 g ( E ) EdE = V ∫0
F
E
E
F
E 2m3 2m3 E 2m 3 2 2 F 2 EdE = V E dE = V E ∫ 0 π2ℏ 3 π2 ℏ 3 π2 ℏ 3 5 F
3
5
E=3E N 5 F
能态密度的更一般形式
g ( E )= dN dE
E k =const.
NZ NZ NZ
自由电子模型的物理思想
◆ 自由电子近似 离子静止，忽略电子和离子实之间的相互作用，电子运动范围 仅受限于晶体表面势垒，被限制在晶体内部 ◆ 独立电子近似 忽略电子和电子之间的相互作用 ◆ 驰豫时间近似
Zn Zm ℏ2 e2 H= −∑ ∇n 2 + ∑′ 1 2 n, m 4πε0 R − R n =1 2M n n m Zn e2 ℏ 2 2 e2 1 1 1 −∑ ∇i + ∑′ −∑∑ 2 i =1 2m i , j 4πε r − r i =1 n=1 4πε r − R i 0 i 0 i j n
kF = 3π2 ne
ℏ 2 kF 2 2m
1/3
108cm -1 2~10eV
费米能量：
EF=
费米动量： 费米速度： 费米温度：
pF = ℏk F
υF = ℏkF /m T F = EF / k B
108cm/s 104 ~105 K 参见表 1.1
单位体积内的平均能量
T=0时，单位体积内的平均能量为：
Drude 模型：应用经典力学，服从经典统计，麦克斯韦- 玻耳兹曼分布 Sommerfeld 模型：应用量子理论，服从量子统计，费米-狄拉克分布
f ( E )= e

《固体物理学》第一二章参考答案

第一章 晶体结构1.1、解：实验表明，很多元素的原子或离子都具有或接近于球形对称结构。

因此，可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。

这样，一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。

它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比，即：晶体原胞的空间利用率， VcnVx =（1）对于简立方结构：（见教材P2图1-1）a=2r ， V=3r 34π，Vc=a 3，n=1∴52.06r8r34a r 34x 3333=π=π=π= （2）对于体心立方：晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯= （3）对于面心立方：晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4，Vc=a 374.062)r 22(r 344a r 344x 3333≈π=π⨯=π⨯= （4）对于六角密排：a=2r 晶胞面积：S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积：V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 74.062r224r 346x 33≈π=π⨯= （5）对于金刚石结构，晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 334.063r 338r 348a r 348x 33333≈π=π⨯=π⨯=1.2、试证：六方密排堆积结构中633.1)38(a c 2/1≈=证明：在六角密堆积结构中，第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形，第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切，于是： NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。

固体物理学第一章1

一个平行六面体的体积等于：V=| 1 • 2 x 3 |。
选取原胞的另一种方式如下：用直线连接一个给定格点的所有近邻格点，在这些 连线的中点作垂直平分线或垂直平分面，这样所包围的最小体积就是维格纳-塞茨 原胞（Wigner-Seitz cell）。
赵铧
16
简单立方晶格的立方单元已是最小的周期性单元，所以就取它为原胞，晶 格基矢1， 2， 3 就沿三个立方边，长短相等：
六角密排晶格的原胞
六角密排晶格的典型单元
Be, Mg, Zn, Cd 等金属
具有六角密排晶格结构
赵铧
7
4. 金刚石晶格
由面心立方单元的中心 到顶角引8条对角线, 在 其中互不相邻的4条对角 线的中点,各加上一个原 子, 就得到金刚石晶格 结构
其特点: 每个原子有4个 最近邻, 它们正 好在一个正四 面体的顶角 A
B
AB
A B
金刚石晶格结构的典型单元
赵铧
8
5. 化合物晶体的结构
(1) 岩盐NaCl晶体结构
它好象是一个简单立方晶格, 但是, 在每一行相间地排列着 正的Na+离子和负的Cl–离子.
碱金属 Li, Na, K, Rb 和卤 族元素 F, Cl, Br, I 的化合物 都具有 NaCl 晶体结构.
Na+
Cl–
Na+
Cl–
NaCl晶格结构中的典型单元
赵铧
9
(2) CsCl晶体结构
它好象一个体心立方, 体心位置有一种离子, 顶角为另一个离子.
体心位置和顶角位置 完全等价, 各占一半, 正好容纳数目相等的 正,负离子.
Cs+ ( Cl– )
Cl– ( Cs+ )

聊城大学固体物理-第一章 1第四节


hu+kv+lw=0
晶带定理
证明： 根据上述结论，晶面(hkl)与下面倒格矢量垂直
Khha*kb*lc* 而晶带轴平行于晶面(hkl)，所以晶带轴与上述倒格矢量垂直，即
(u a vbw c)•(h a * kb * lc*)0
2 (h u k vlw )0
h uk vlw 0 晶带定理适用所有晶系
聊城大学物理科学与信息工程学院
P
b3 a3
O
a
b1
1
b2
a2
设a1a2， a2 a3， a3a1面族的面间距分别为d3，d1， d2。
作OP垂直a1a2面，并另OP= b3，使b3=2π/ d3。 同理，对于a2 a3面，得到b1 = 2π/ d1 ； 对于 a3a1面，得到b2 = 2π/ d2。
因此得到三个矢量 b1， b2， b3，称为倒格子基矢。
表示变量：
x1
1
2
b1
•
x
xx1a1x2a2x3a3
1
x2 2 b2 •x
1
x3 2 b3 •x
所以 V ( x 1 ,x 2 ,x 3 )V h 1 h 2 h 3 e x [ 2 p i( h 1 x 1 h 2 x 2 h 3 x 3 )]
h 1 h 2 h 3
V hh 2h 3ex i(h 1 p b 1h 2b 2h 3b 3)•x
b3
2π a
j k
a1
a 2
i
j
a2a2 ik
a3
该函数可以看成以x1、x2 、x3为变量，周期为 l 的周期函数，其傅 立叶级数表示如下：
V ( x 1 ,x 2 ,x 3 )V h 1 h 2 h 3 e x [ 2 p i( h 1 x 1 h 2 x 2 h 3 x 3 )]

固体物理 1(1)

Rl=l1a1+l2a2+l3a3 式中l1、l2、l3是整数。若l1、l2、l3是互质，就直接用 [l1,l2,l3] 来表示晶列OA的方向。
(2) 晶面
平行的晶面把所有的格点包括无遗。
晶面的表示方法 一个晶面的取向可以由这个晶面上任意三个不共线的 点确定。如果这三个点处在不同的晶轴上，则可以由 晶格常量 a1a2a3 表示的点的坐标就能标定它们所决定 的晶面。
简单正交
底心正交
体心正交
面心正交
正交晶系有4种晶格：简单正交 ; 底心正交; 体心正交 ; 面心正交
(4) 正方晶系(四角晶系)
900
a1 a2 a3
简单四角 体心四角
四角晶系有两种晶格：简单四角; 体心四角
(5) 六角晶系
90
0
1200
a1 a 2
立方晶系晶面指数
1． 5
典型的晶体结构
氯化纳结构
其晶格属于面心立方，基元由一个Na+和一个Cl+ 。从图中看， 如果只看Cl+，它构成面心立方结构，同样Na+也构成面心立方。 这两个面心立方子晶格各自的原胞具有相同的基矢，只不过互 相有一个位移。
氯化铯晶体结构
其晶格属于简单立方，基元由一个位于000的铯离子和一个 位于1/2 1/2 1/2 的氯离子组成。
周期晶格不 可能存在五 重对称轴， 因为不可能 使五边形相 互连接的陈 列不留空隙 地充满整个 空间。
图1-4
(3) 镜面反映 ，它是以通过一个格点的平面作为反映平 面的对称操作。 (x1,x2,x3)

(x1,x2,-x3)
(4) 反演操作是先转动 弧度之后在垂直于其转动轴的 一个平面上反映，总的效果是
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

a2
1
a 2
a1
2
a2
3
a1
a 2
4
a1
a1
二维晶格的空间格点示意图。图中每对a1和a2都是晶格
平移矢量，但是， a1 和 a 2 不是初基平移矢量，因为不
第一章 晶体结构
第二章 晶体结构测定
第三章 晶格振动
第四章 金属（I）：自由电子
第五章 金属（II）：能带论
第一章(1) 晶体结构
1.1 晶体的共性
1.2 一些晶格的实例 1.3 配位数和致密度
1.4 原子的周期性阵列
1.5 晶格的基本类型
1.6 再总结：布喇菲格子
固体的结构：固体材料是由大量的原子（或离子）组成的，原 子以一定方式排列，原子排列的方式称为固体的 结构。
三、各向异性
晶体的物理性质是各向异性的：
1、平行石英的c轴入射单色光，不产生双折射；而沿其它方向入射产生单色光； 2、晶体沿某些确定方位的晶面发生解理的现象：方解石、云母。
由于晶体的物理性质是各向异性的，因此有些物理常数一般不能用一 个数值来表示。例如弹性常数、压电常数、介电常数、电导率等一般 需要用张量来描述。 晶体的各向异性是晶体区别于非晶体的重要特征。
五、六角密堆积
若第三层的原子球心落在第二层的空隙上，且与第一层平行对应， 就构成 了六角密堆积。
A
B A
六角密排晶格的典型单元
AB AB AB
Be、Mg、Zn、Cd等具有六角密排晶格结构
六、立方密堆积
若第三层的原子球心落在第二层的空隙上，且该空隙也与第一层 原子空隙重合，而第四层又恢复成第一层的排列，这就构成 了立 方密堆积。 每个原子和最近邻的原子之间都是相切的。
Rl l1 a1 l2 a 2 l3 a 3
（1）初基平移矢量的定义确保了没有比这组矢量所构成的体
积 a1 a 2 a 3 更小的晶胞，可作为晶体结构的“砌


块”； （2）通常用初基平移矢量来定义晶轴，这些晶轴构成初基平 行六面体的三个邻边。 （3）有时，非初基晶轴与结构对称性有更简单的关系，此时 也可以采用非初基晶轴。
固体物理
陈之战
2012年9月19日
固体物理学发展概况
最早发展的是矿物学，为了鉴别矿石，产生了晶体学，在
黄昆 1919-2005
19世纪发展到相当完善的地步。此外，由于冶金的发展，产生
了金属学，对固体的电学、磁学、光学的性质也进行 了细致的
研究。不仅如此，对晶体的微观结构也有研究，如将晶体外形 的规则性与内部原子的规则排列联系起来。 20世纪开始，电子论有很大的发展，对固体的电学、磁性、 光学性质发展了理论，然而是较简单的。由于X射线的发现， 对原子结构有了很好的了解，并且用X射线研究了原子排列， 使得对原子如何结合成为晶体的认识大大深入了一步。量子力 学提高了经典的电子论，使得更深刻地理解固体的电学、磁学、 光学性质。此外，技术的发展大大利用了固体的性质。
（3）对同一空间点阵，原胞的体积均相等。
原胞的选取原则：
原则上只要是最小周期性单元都可以，也就是说仅在平行六 面体的八个顶角上存在阵点，但原胞的体积都相等，且原胞 仅反映晶格的周期性，不能反映晶体的对称性。 为了反映晶体的对称性，需要引入晶胞的概念。
对于二维晶体的原胞，则要求在周期性结构单元的前提下， 面积最小，且周长最短。 通常原胞作为最小（体积最小）的周期性结构单元的判据是 一个原胞中只包含一个基元。该判据只是原胞的一个必要判 据，如果一个单元含有两个或两个以上的基元，该单元就肯 定不是原胞。
的最大配位数为12，最大的致密度为0.74。
思考题：以堆积模型计算由同种原子构成的铜体积的体心 和面心立方晶体中的原子数之比。（0.919）
1.4 原子的周期性阵列
一、晶格平移矢量
在理想情况下，晶体是由全同的原子 团在空间无限重复排列而构成的，这 样的原子团被称为基元（basis）。 在数学上，这些基元可以抽象为几何 点，而这些点的集合被称为晶格 （lattice）。 在三维情况下，晶格可以通过三个平 移矢量a1、a2、a3来表示。 （a）空间格点
列的，这种至少在微米数量级范围的有序排列，称为长程有序。 晶体分为单晶体和多晶体，多晶体是由许许多多小单晶（晶粒）
构成。对于单晶体，在整个范围内原子都是规则排列的；对于多
晶体，在各晶粒范围内，原子是有序排列的。
二、自限性
晶体具有自发地形成封闭几何多面体的特
性，称之为晶体的自限性。这一特性是晶
体内部原子的规则排列在晶体宏观形态上 的反映。 理想石英晶体
（b）基元，包含两个不同的原子
（c）晶体结构
晶体结构是这样形成的，即将基元（b）配置 在晶格（a）的每个格点上，通过考察（c） 可以辨认基元，然后可引出空间格点。
数学定义：如果选择一组不共面的平移矢量（a1、a2、a3 ，也称为基 矢），那么用整数l1、l2、l3和基矢组成的矢量（也称为格矢，位矢）
1.2 一些晶格的实例
晶格：晶体中原子排列的具体形式称为晶体格子，简称晶格。 （1）晶体原子规则排列形式不同，则有不同的晶格结构；
（2）晶体原子规则排列形式相同，只是原子间的距离不同，
则它们具有相同的晶格结构。
处理方法：把晶格设想成为原子球的规则堆积
一、正方堆积
把原子视为刚性小球，在二维平面内最 简单的规则堆积便是正方堆积； 任一个球与同一平面内的四个最近邻相 切。 原子球的正方堆积
基矢（basis）：指原胞的边矢量， 三维格子的重复单元是平行六面体， a1、a2、a3是重复单元的边长矢量。
特点：
（1）空间点阵中体积最小的重复单元
a1 a 2 a 3


（2）空间点阵中每个固体物理原胞只包含一个格点
如果原胞是一个平行六面体，那么每个角上的格点 将分属于在该处相毗邻的八个晶胞，有81/8=1， 即每个原胞中只含有一个格点。
设晶格常数为a，粒子半径为r，则：
3a 2 4r a 2 4r a 2
2
晶胞中含有4个粒子，则面心立方结 构的致密度为： 4 4 r3 3 Db 0.74 3 a
三、HCP堆积的致密度
对于六角密堆积结构，任一个原子有12个最近邻。若原子以刚性球堆积，中心在1 的原子与中心在2、3、4的原子相切，中心在5的原子与中心在6、7、8的原子相切， 晶胞内的原子O与中心在1、3、4、5、7、8处的原子相切，即O点与中心在5、7、 8处的原子分布在正四面体的四个顶上。因为四面体的高：
晶体：原子排列具有周期性（长程有序） 固 体 材 料
非晶体：原子排列不具有长程的周期性
准晶体：1984年从实验中观察到，既区别于晶体又 区别于非晶体的固体材料
固体中原子排列的形式是研究固体材料的宏观性质和各 种微观过程的基础。
1.1 晶体的共性
一、长程有序
长程有序是晶体最突出的特点。晶体中的原子都是按一定规则排
Rl l1 a1 l2 a 2 l3 a 3
（1）所给出的所有空间点的集合称为晶格，也称为空间点阵、点阵、Bravias格子、 格子； （2）基矢可以有多种选择，一般选最短；
格矢的重要特点：任何一个格矢可由另两个格矢的和来表示，
Rl 的外形
会有差异。在某条件下生长的晶体的晶面 数目和相对大小，与另一条件下生长的同
一种晶体的晶面情况会有很大的差别。
一种人造晶体
尽管同一种晶体其外形可能不同，但相应 的两晶面之间的夹角总是不变的，这一规 律称为晶面夹角守恒定律。
mm两面夹角：600' mR两面夹角：3813' mr两面夹角：3813'
• •
二、结构基元与晶体结构
• 晶轴一旦选定，晶体结构的基元也就可以确定下来。这里 所说的晶格的格点只是为了描述上的方便，是数学抽象。 对于给定的晶体，其中的所有基元无论在组成、排列还是 在取向方面都是完全相同的。 基元中原子数目可以是一个，也可以多于一个。基元中第j 个原子的中心位置相对于一个格点可用下式表示：
晶体=几何结构（数学）+基本重复单元（物理）
• 基元：原子、分子或由多个原子构成的集团。如用几何点代表基元，那么几 何点在空间排列成晶格（点阵、格子），基元加在格点上形成晶体。 • • 格点（结点）：基元位置，代表基元的几何点 晶格：格点（结点）的总和，又称为空间点阵（点阵）和Bravais格子（格 子）。晶格是晶体结构的数学表示，晶格中的每个格点代表基元，不要和代 表原子的小球混淆。
配位是的大小描述晶体中粒子排列的紧密程度：粒子排列越紧密，配位数越大。
一、BCC堆积的致密度
设晶格常数为a，粒子半径为r，则：
a 2 2a 2 4r 4r a 3
2
晶胞中含有2个粒子，则BCC结构的致密度： 4 2 r3 3 Db 0.68 3 a
二、FCC堆积的致密度
ABC立方密堆积
面心立方晶格的典型单元
ABC
ABC ABC
Cu、Ag、Au、Al等具有面心立方晶格结构
1.3 配位数和致密度
晶体中一个原子的最近邻原子数目称为配位数。
（1）体心立方点阵：每一个阵点的最近邻阵点有8个，配位数是8；
（2）面心立方点阵：每一个阵点的最近邻阵点有12个，配位数是12。
h 2 2 c a2 r 3 3 2
晶胞体积：V
ca 2 sin 60o
4 a 2 3 2 一个晶胞内包含两个原子，所以： Db 0.74 3 2 ca 2
3 2 ca 2
3
密堆积（面心立方、六角）结构的致密度是自然界中硬球
排列的最紧密的结构之一，即硬球排列的所有可能方式中
这总是成立的，因为任何一个格矢总是由三个整数（比如l1、l2、