固体物理总结 第一章 晶体的结构
- 格式:pdf
- 大小:746.88 KB
- 文档页数:20


第1章晶体的结构(1)固体物质是由大量的原子、分子或离子按照一定方式排列而成的,这种微观粒子的排列方式称为固体的微结构。
(2)按照微结构的有序程度,固体分为晶体、准晶体和非晶体三类。
其中,晶体的研究已经非常成熟,而非晶体和准晶体则是固体研究的新领域。
(3)晶体的结构和特性决定了它在现代科学技术上有着及其广泛的应用,因此,固体物理学以晶体作为主要的研究对象。
§1.1 晶体的基本性质一、晶体的特征1.长程有序*虽然不同的晶体具有各自不同的特性,但是,在不同的晶体之间仍存在着某些共同的特征,这主要表现在以下几个方面。
*具有一定熔点的固体,称为晶体。
*实验表明:在晶体中尺寸为微米量级的小晶粒内部,原子的排列是有序的。
在晶体内部呈现的这种原子的有序排列,称为长程有序。
*长程有序是所有晶体材料都具有的共同特征,这一特性导致晶体在熔化过程中具有一定的熔点。
*晶体分为单晶体和多晶体。
在单晶体内部,原子都是规则地排列的。
单晶体是个凸多面体,围成这个凸多面体的面是光滑的,称为晶面。
(1)单晶体( Single Crystal )由许多小单晶(晶粒)构成的晶体,称为多晶体。
多晶体仅在各晶粒内原子才有序排列,不同晶粒内的原子排列是不同的。
(2)多晶体( Multiple Crystal )由许多小单晶(晶粒)构成的晶体,称为多晶体。
多晶体仅在各晶粒内原子才有序排列,不同晶粒内的原子排列是不同的。
*晶面的大小和形状受晶体生长条件的影响,它们不是晶体品种的特征因素。
2.解理(Cleavage)(1)晶体具有沿某一个或数个晶面发生劈裂的特征,这种特征称为晶体的解理。
解理的晶面,称为解理面。
(2)有些晶体的解理性比较明显,例如,NaCl晶体等,它们的解理面常显现为晶体外观的表面。
(3)有些晶体的解理性不明显,例如,金属晶体等。
(4)晶体解理性在某些加工工艺中具有重要的意义,例如,在划分晶体管管芯时,利用半导体晶体的解理性可使管芯具有平整的边缘和防止无规则的断裂发生,以保证成品率。

固体物理(黄昆)第一章总结.doc固体物理(黄昆)第一章总结固体物理学是一门研究固体物质微观结构和宏观性质的学科。
黄昆教授的《固体物理》一书为我们提供了深入理解固体物理的基础。
本总结旨在概述第一章的核心内容,包括固体的分类、晶体结构、晶格振动和固体的电子理论。
一、固体的分类固体可以根据其结构特征分为晶体和非晶体两大类。
晶体具有规则的几何外形和有序的内部结构,而非晶体则没有长程有序性。
晶体又可以根据其内部原子排列的周期性分为单晶体和多晶体。
二、晶体结构晶体结构是固体物理学的基础。
黄昆教授详细讨论了晶格、晶胞、晶向和晶面等概念。
晶格是描述晶体内部原子排列的数学模型,而晶胞是晶格的最小重复单元。
晶向和晶面则分别描述了晶体中原子排列的方向和平面。
三、晶格振动晶格振动是固体物理中的一个重要概念,它涉及到晶体中原子的振动行为。
黄昆教授介绍了晶格振动的量子化描述,包括声子的概念。
声子是晶格振动的量子,它们与晶体的热传导和电导等性质密切相关。
四、固体的电子理论固体的电子理论是固体物理学的核心内容之一。
黄昆教授从自由电子气模型出发,介绍了固体中电子的行为和性质。
自由电子气模型假设电子在固体中自由移动,不受原子核的束缚。
这一模型可以解释金属的导电性和热传导性。
五、能带理论能带理论是固体电子理论的一个重要组成部分。
黄昆教授详细讨论了能带的形成、能隙的概念以及电子在能带中的分布。
能带理论可以解释不同固体材料的导电性差异,是现代半导体技术和电子器件设计的基础。
六、固体的磁性固体的磁性是固体物理中的另一个重要主题。
黄昆教授讨论了磁性的来源,包括原子磁矩和电子自旋。
磁性固体可以分为顺磁性、抗磁性和铁磁性等类型,它们的磁性行为与电子结构密切相关。
七、固体的光学性质固体的光学性质涉及到固体对光的吸收、反射和透射等行为。
黄昆教授介绍了固体的光学性质与电子结构之间的关系,包括光的吸收和发射过程。
八、固体的热性质固体的热性质包括热容、热传导和热膨胀等。



第一章晶体结构⏹布拉菲点阵概念⏹惯用晶胞(单胞)概念⏹初基晶胞(原胞)概念⏹Wigner-Seize晶胞⏹晶体结构基元+点阵=晶体结构⏹简单的晶体结构(1)sc,bcc,fcc结构的特征(2)金刚石结构(3)六角密堆积结构(4)NaCl结构(5)CsCl结构⏹晶列, 晶向, 晶面, 晶面族, 晶面指数, 密勒指数, 晶面间距晶面指数(hkl)的定义和求法方向指数[abc]的定义和求法⏹对称操作⏹7种晶系和14种布拉菲点阵1以堆积模型计算由同种原子构成的同体积的简立方和面心立方晶体中的原子数之比。
2证明立方晶系的晶列[hkl]与晶面族(hkl)正交3某元素晶体的结构为体心立方布拉菲格子,试指出其格点面密度最大的晶面系的密勒指数,并求出该晶面系相邻晶面的面间距4在立方晶胞中画出(122),(001),(10),(210)晶面和[122]5晶体中可以独立存在的8种对称元素是:、、、、、、、。
⏹布拉格定理⏹倒易点阵初基矢量公式⏹布里渊区的求法(二维正方格子和长方格子)⏹实验衍射方法(劳厄法、转动晶体法和粉末法)⏹倒易点阵矢量和晶面指数间的关系1考虑晶体中一组互相平行的点阵平面(hkl),(a)证明倒易点阵矢量G(hkl)=hb1+kb2+lb3垂直于这组平面(hkl);(b)证明两个相邻的点阵平面间的距离d(hkl)为2从体心立方铁的(110)平面来的X-射线反射的布喇格角为22º,X-射线波长λ=1.54Å。
试计算铁的立方晶胞边长;(b)从体心立方结构铁的(111)平面来的反射的布喇格角是多少?答案:a)a=2.91Å;b)θ=27.28º3对于点阵常数为a的二维六角点阵,(a)写出正点阵的初基矢量;(b )计算倒易点阵的初基矢量;(c )画出第一、第二、第三布里渊区;(d )计算第一布里渊区的体积。
4半导体材料Si 和Ge 单晶的晶体点阵类型为 ,倒易点阵类型为 ,第一布里渊区的形状为 ,每个 原子的最近邻原子数为 。
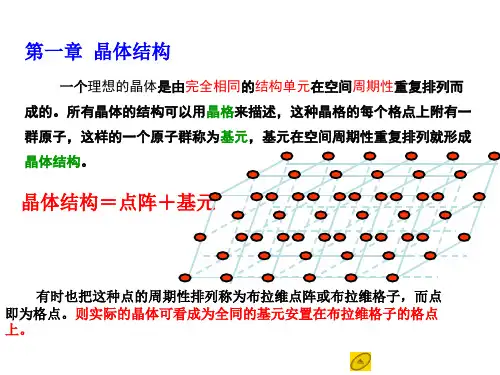



第一章 晶体结构1.晶体:组成固体的原子(或离子)在微观上的排列具有长程周期性结构;eg :单晶硅。
晶体具有的典型物理性质:均匀性、各向异性、自发的形成多面体外形、有明显确定的熔点、有特定的对称性、使X 射线产生衍射。
非晶体:组成固体的粒子只有短程序,但无长程周期性;eg :非晶硅、玻璃准晶:有长程的取向序,沿取向序的对称轴方向有准周期性,但无长程周期性,不具备晶体的平移对称性;eg :快速冷却的铝锰合金2.三维晶体中存在7种晶系14种布拉菲格子;对于简单格子晶胞里有几个原子就有几个原胞,复式格子中包含两个或更多的格子。
3.典型格子特点:sc bcc fcc hcp Diamond 晶胞体积3a 3a 3a 32a 3a 每晶胞包含的格点数1 2 4 6 8 原胞体积3a 321a 341a 332a 341a 最近邻数(配位数)6 8 12 12 4 填充因子0.524 0.68 0.74 0.74 0.34 典型晶体 NaCl CaO Li K Cu Au Zn Mg Si Ge4.sc 正格子基矢:k a a j a a i a a ===321,,;sc 倒格子基矢:k ab j a i a πππ2,2b ,2b 321===; fcc 正格子基矢:)2),2),2321j i a a k i a a k j a a +=+=+=(((; fcc 倒格子基矢:)2),2),2b 321k j i ab k j i a b k j i a -+=+-=++-=(((πππ; bcc 正格子基矢: )2),2),2321k j i a a k j i a a k j i a a -+=+-=++-=(((; bcc 倒格子基矢:)2),2),2b 321j i a b k i a b k j a +=+=+=(((πππ; 倒格子原胞基V a a )(2b 321⨯=π,V a a )(2b 132⨯=π,Va a )(2b 213⨯=π 正格子和倒格子的基矢关系为ij a πδ2b j i =⋅;设正格子原胞体积为V,倒格子原胞体积为Vc ,则3)2(V c V π=⨯。

第一章 晶体结构1、试说明空间点阵和晶体结构的区别。
答:空间点阵是晶体中质点排列的几何学抽象,用以描述和分析晶体结构的周期性和对称性,它是由几何点在三维空间理想的周期性规则排列而成,由于各阵点的周围环境相同,它只能有14种类型。
晶体结构则是晶体中实际质点(原子、离子或分子)的具体排列情况,它们能组成各种类型的排列,因此实际存在的晶体结构是无限的。
当晶格点阵中的格点被具体的基元代替后才形成实际的晶体结构。
2、证明体心立方格子和面心立方格子互为倒格子证明:(1)面心立方的正格子基矢(固体物理学原胞基矢):123()2()2()2a a j k a a i k a a i j ⎧=+⎪⎪⎪=+⎨⎪⎪=+⎪⎩rr r r r rr r r由倒格子基矢的定义:1232()b a a π=⨯Ωr r r31230,,22(),0,224,,022a a a a a a a a a a Ω=⋅⨯==r r rQ ,223,,,0,()224,,022i j ka a a a a i j k a a ⨯==-++r rr r r r r r213422()()4a b i j k i j k a aππ∴=⨯⨯-++=-++r r rr r r r同理可得:232()2()b i j k ab i j k aππ=-+=+-r r r r r r r r 即面心立方的倒格子基矢与体心立方的正格基矢相同。
所以,面心立方的倒格子是体心立方。
(2)体心立方的正格子基矢(固体物理学原胞基矢):123()2()2()2aa i j kaa i j kaa i j k ⎧=-++⎪⎪⎪=-+⎨⎪⎪=+-⎪⎩rr rrrr rrrr rr由倒格子基矢的定义:1232()b a aπ=⨯Ωr r r3123,,222(),,2222,,222a a aa a a aa a aa a a-Ω=⋅⨯=-=-r r rQ,223,,,,()2222,,222i j ka a a aa a j ka a a⨯=-=+-rr rrrr r213222()()2ab j k j ka aππ∴=⨯⨯+=+r r rr r同理可得:232()2()b i kab i jaππ=+=+r rrr r r即体心立方的倒格子基矢与面心立方的正格基矢相同。
一、考试重点晶体结构、晶体结合、晶格振动、能带论的基本概念与基本理论与知识二、复习内容第一章晶体结构基本概念1、晶体分类及其特点:单晶粒子在整个固体中周期性排列非晶粒子在几个原子范围排列有序(短程有序)多晶粒子在微米尺度内有序排列形成晶粒,晶粒随机堆积准晶体粒子有序排列介于晶体与非晶体之间2、晶体的共性:解理性沿某些晶面方位容易劈裂的性质各向异性晶体的性质与方向有关旋转对称性平移对称性3、晶体平移对称性描述:基元构成实际晶体的一个最小重复结构单元格点用几何点代表基元,该几何点称为格点晶格、平移矢量基矢确定后,一个点阵可以用一个矢量表示,称为晶格平移矢量基矢元胞以一个格点为顶点,以某一方向上相邻格点的距离为该方向的周期,以三个不同方向的周期为边长,构成的最小体积平行六面体。
原胞就是晶体结构的最小体积重复单元,可以平行、无交叠、无空隙地堆积构成整个晶体。
每个原胞含1个格点,原胞选择不就是唯一的晶胞以一格点为原点,以晶体三个不共面对称轴(晶轴) 为坐标轴,坐标轴上原点到相邻格点距离为边长,构成的平行六面体称为晶胞。
晶格常数WS元胞以一格点为中心,作该点与最邻近格点连线的中垂面,中垂面围成的多面体称为WS原胞。
WS原胞含一个格点复式格子不同原子构成的若干相同结构的简单晶格相互套构形成的晶格简单格子点阵格点的集合称为点阵布拉菲格子全同原子构成的晶体结构称为布拉菲晶格子。
4、常见晶体结构:简单立方、体心立方、面心立方、金刚石闪锌矿铅锌矿氯化铯氯化钠钙钛矿结构5、密排面将原子瞧成同种等大刚球,在同一平面上,一个球最多与六个球相切,形成密排面密堆积密排面按最紧密方式叠起来形成的三维结构称为密堆积。
六脚密堆积密排面按AB\AB\AB…堆积立方密堆积密排面按ABC\ABC\ABC…排列5、晶体对称性及分类:对称性的定义晶体绕某轴旋转或对某点反演后能自身重合的性质对称面对称中心旋转反演轴8种基本点对称操作14种布拉菲晶胞32种宏观对称性7个晶系6、描述晶体性质的参数:配位数晶体中一个原子周围最邻近原子个数称为配位数。