固体物理第一章习题解答

第一章、晶体的结构习题1.以刚性原子球堆积模型，计算以下各结构的致密度分别为:(1)简立方，！; (2)体心立方，—7T；(5)念刚石结构，—-7T,16［解答］设晶体是由刚性原子球堆积而成，一个晶胞中刚性原子球占据的体积与晶胞体职的比值称为结构的致密度，设n为一个晶胞中的刚性原子球数，表示刚性原子球半径，r表示晶胞体4 3n — 7D'积，则致密度p =(1) 对简立方晶体，任一个原子有6个最近邻，若原子以刚性球堆积，如图1.2所示，中心在1, 2, 3, 4处的原子球将依次相切，因为= 4r，厂=a3,面1.2简立方晶胞晶胞内包含1个原子，所以(2)对体心立方晶体，任一个原子有8个最近邻，若原子刚性球堆积，如图1.3所示，体心位置O的原子8个角顶位置的原子球相切，因为晶胞空间对角线的长度为力〃=4r,K = a\晶胞闪包含2个原子，所以(3)面心立方，(4)六角密积，2图1.3体心立方晶胞(3) 对面心立方晶体，任一个原子有12个最近邻，若原子以刚性球堆积， 如图1.4所示，中心位于角顶的原子与相邻的3个面心原子球相切，因为 42a = 4r,V = a\ 1个晶胞内包含4个原子，所以图1.4面心立方晶胞(4) 对六角密积结构，任一个原子有12个最近邻，若原子以刚性球堆积， 如图1。

5所示，屮心在1的原子与屮心在2，3，4的原子相切，中心在5的原 子与中心在6，7，8的原子相切，图1.5六角晶胞 图1.6正叫面体晶胞闪的原子O 与屮心在1，3, 4, 5, 7, 8处的原子相切，即O 点与屮心在5, 7, 8处的原子分布在正四面体的四个顶上，因为四面体的高11=^ = 2^ = ~一个晶胞内包含两个原子，所以晶胞体积V= ca 2 sin 60 ca ^ea 22*音吨)3(5) 对金刚石结构，任一个原子有4个最近邻，若原子以刚性球堆积，如 图1.7所示，中心在空间对角线四分之一处的0原子与中心在1，2，3, 4处的 原子相切，因为 43a = 8r,晶胞体积 V = a\图1.7金刚石结构 一个晶胞A 包含8个原子，所以/?2.在立方晶胞中，画出(102), (021), (122 )，和(210)晶面。

《固体物理学》习题解答黄昆 原著 韩汝琦改编 （陈志远解答，仅供参考）第一章 晶体结构1.1、解：实验表明，很多元素的原子或离子都具有或接近于球形对称结构。

因此，可以把这些原子或离子构成的晶体看作是很多刚性球紧密堆积而成。

这样，一个单原子的晶体原胞就可以看作是相同的小球按点阵排列堆积起来的。

它的空间利用率就是这个晶体原胞所包含的点的数目n 和小球体积V 所得到的小球总体积nV 与晶体原胞体积Vc 之比，即：晶体原胞的空间利用率， VcnVx = （1）对于简立方结构：（见教材P2图1-1）a=2r ， V=3r 34π，Vc=a 3，n=1 ∴52.06r 8r34a r 34x 3333=π=π=π= （2）对于体心立方：晶胞的体对角线BG=x 334a r 4a 3=⇒= n=2, Vc=a 3∴68.083)r 334(r 342a r 342x 3333≈π=π⨯=π⨯=（3）对于面心立方：晶胞面对角线BC=r 22a ,r 4a 2=⇒= n=4，Vc=a 374.062)r 22(r 344a r 344x 3333≈π=π⨯=π⨯= （4）对于六角密排：a=2r 晶胞面积：S=6260sin a a 6S ABO ⨯⨯=⨯∆=2a 233 晶胞的体积：V=332r 224a 23a 38a 233C S ==⨯=⨯ n=1232126112+⨯+⨯=6个 74.062r224r346x 33≈π=π⨯= （5）对于金刚石结构，晶胞的体对角线BG=3r 8a r 24a 3=⇒⨯= n=8, Vc=a 334.063r 338r 348a r 348x 33333≈π=π⨯=π⨯=1.2、试证：六方密排堆积结构中633.1)38(a c 2/1≈= 证明：在六角密堆积结构中，第一层硬球A 、B 、O 的中心联线形成一个边长a=2r 的正三角形，第二层硬球N 位于球ABO 所围间隙的正上方并与这三个球相切，于是： NA=NB=NO=a=2R.即图中NABO 构成一个正四面体。

第一章、 晶体的结构习 题1． 以刚性原子球堆积模型，计算以下各结构的致密度分别为： （1）简立方，6π; （2）体心立方, ;83π （3）面心立方，;62π （4）六角密积，;62π （5）金刚石结构，;163π [解答]设想晶体是由刚性原子球堆积而成，一个晶胞中刚性原子球占据的体积与晶胞体积的比值称为结构的致密度，设 n 为一个晶胞中的刚性原子球数,r 表示刚性原子球半径，V 表示晶胞体积，则致密度ρ=Vr n 334π（1） 对简立方晶体，任一个原子有6个最近邻，若原子以刚性球堆积，如图1.2所示，中心在1，2，3，4处的原子球将依次相切，因为,,433a V r a ==面1.2 简立方晶胞 晶胞内包含1个原子，所以ρ=6)(33234ππ=aa（2）对体心立方晶体，任一个原子有8个最近邻，若原子刚性球堆积，如图1.3所示，体心位置O 的原子8个角顶位置的原子球相切，因为晶胞空间对角线的长度为,,433a V r a ==晶胞内包含2个原子，所以ρ=ππ83)(*2334334=a a图1.3 体心立方晶胞（3）对面心立方晶体，任一个原子有12个最近邻，若原子以刚性球堆积，如图 1.4所示，中心位于角顶的原子与相邻的3个面心原子球相切，因为3,42a V r a ==，1个晶胞内包含4个原子，所以ρ=62)(*4334234ππ=a a .图1.4面心立方晶胞（4）对六角密积结构，任一个原子有12个最近邻，若原子以刚性球堆积，如图1。

5所示，中心在1的原子与中心在2，3，4的原子相切，中心在5的原子与中心在6，7，8的原子相切，图 1.5 六角晶胞 图 1.6 正四面体晶胞内的原子O 与中心在1，3，4，5，7，8处的原子相切，即O 点与中心在5，7，8处的原子分布在正四面体的四个顶上，因为四面体的高h =223232c r a == 晶胞体积 V = 222360sin ca ca =, 一个晶胞内包含两个原子，所以ρ=ππ62)(*22233234=ca a .（5）对金刚石结构，任一个原子有4个最近邻，若原子以刚性球堆积，如图1.7所示，中心在空间对角线四分之一处的O 原子与中心在1，2，3，4处的原子相切，因为,83r a =晶胞体积 3a V =,图1.7金刚石结构一个晶胞内包含8个原子，所以ρ=163)83(*83334ππ=aa . 2．在立方晶胞中，画出（102），（021），（122-），和（201-）晶面。

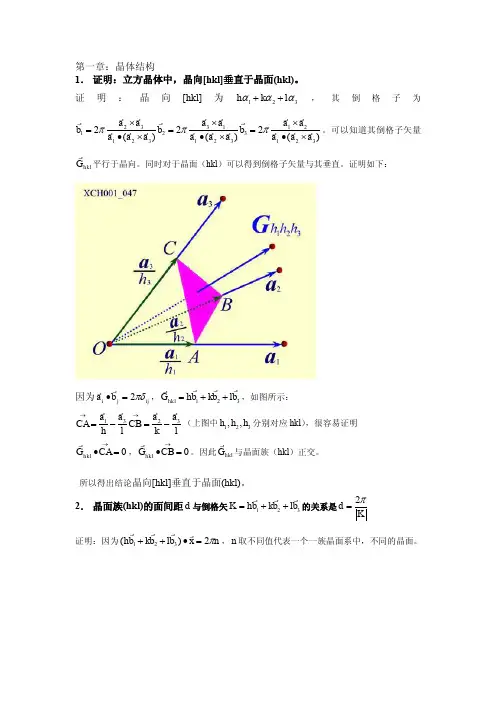
第一章 参考答案1体心立方格子和面心立方格子互为正倒格子，试证明之。

证：体心立方格子的固体物理学原胞（Primitive cell ）的三个基矢是)(2),(2),(2321→→→→→→→→→→→→-+=+-=++-=k j i a a k j i a a k j i a a ⎪⎪⎪⎭⎪⎪⎪⎬⎫+=+=+==⨯⋅=ΩΩ⨯=Ω⨯=Ω⨯=→→→→→→→→→→→→→→→→→→→→→)(2)(2)(22122,2:3213321213132321j i a b i k a b k j ab aa a a a ab a a b a a b ππππππ定义它们是倒点阵面心立方的三个基矢。

2 对六角密堆积结构固体物理学原胞基矢如→→→→→→→→=+-=+=kc a ja i a a j a i a a 321232232求倒格子基矢。

解：;,213→→→⊥a a a→→→→→→→→+-=+===ja i a a ja i a a a a a 2322322121)33(32)32(22332123213→→→→→→→→→→→→+=+Ω=Ω⨯==⨯⋅=Ω=j i aac a i ac j a a b ca aa a a kc a πππ ⎪⎭⎫ ⎝⎛+-=Ω⎪⎭⎫ ⎝⎛⨯=→→→→→j i a a a b 3332/2132ππ→→→→=Ω⎪⎭⎫⎝⎛⨯=kc a a b ππ2/22133求解简单立方中晶面指数为(hkl)的晶面簇间距。

解：正格子基矢是 →→→→→→===k a c j a b i a a ,,令 为相应的倒基矢→→→***,,c b a21222***,,3***)()()(2222)(222-→→→→→→→→→→→→→→→→→⎥⎦⎤⎢⎣⎡++==++=++==⨯⋅=Ω===a l a k ahK d kl a j k a i h a c l b k a h K a c b a kac j ab i aa hklnkl l k h πππππππ4 试证明六角密集结构中c/a=如图所示，ABC 分别表示六角密排结构中三个原子，D 表示中心的原子。

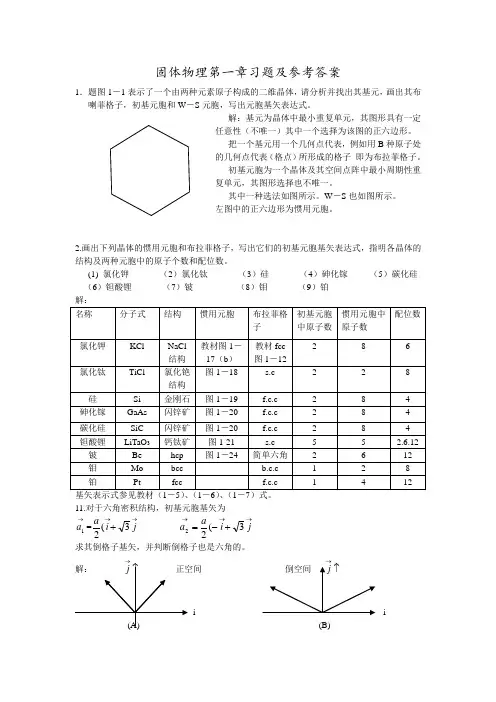
固体物理第一章习题及参考答案1．题图1－1表示了一个由两种元素原子构成的二维晶体，请分析并找出其基元，画出其布喇菲格子，初基元胞和W －S 元胞，写出元胞基矢表达式。

解：基元为晶体中最小重复单元，其图形具有一定任意性（不唯一）其中一个选择为该图的正六边形。

把一个基元用一个几何点代表，例如用B 种原子处的几何点代表（格点）所形成的格子 即为布拉菲格子。

初基元胞为一个晶体及其空间点阵中最小周期性重复单元，其图形选择也不唯一。

其中一种选法如图所示。

W －S 也如图所示。

左图中的正六边形为惯用元胞。

2.画出下列晶体的惯用元胞和布拉菲格子，写出它们的初基元胞基矢表达式，指明各晶体的结构及两种元胞中的原子个数和配位数。

(1) 氯化钾 （2）氯化钛 （3）硅 （4）砷化镓 （5）碳化硅 （6）钽酸锂 （7）铍 （8）钼 （9）铂 解：基矢表示式参见教材（1－5）、（1－6）、（1－7）式。

11.对于六角密积结构，初基元胞基矢为→1a =→→+j i a 3(2 →→→+-=j i a a 3(22求其倒格子基矢，并判断倒格子也是六角的。

倒空间 ↑→ji i (B)由倒格基失的定义，可计算得Ω⨯=→→→3212a a b π=a π2)31(→→+j i →→→→→+-=Ω⨯=j i a a a b 31(22132ππ→→→→=Ω⨯=k ca ab ππ22213正空间二维元胞（初基）如图（A ）所示，倒空间初基元胞如图（B ）所示（1）由→→21b b 、组成的倒初基元胞构成倒空间点阵，具有C 6操作对称性，而C 6对称性是六角晶系的特征。

（2）由→→21a a 、构成的二维正初基元胞，与由→→21b b 、构成的倒初基元胞为相似平行四边形，故正空间为六角结构，倒空间也必为六角结构。

12．用倒格矢的性质证明，立方晶格的（hcl ）晶向与晶面垂直。

证：由倒格矢的性质，倒格矢→→→→++=321b l b k b h G hkl 垂直于晶面（h 、k 、l ）。